«Транспорттық тапсырма»

КІРІСПЕ 3
IТРАНСПОРТТЫҚ ТАПСЫРМА 4
1.1 Транспорттық есеп. 4
1.2 Транспорттық модельдерді шешу әдістеріне қысқаша шолу 8
1.3 Транспорттық есепті желілік әдіспен шешу ... ...12
1.4 Транспорттық есептің математикалық моделі ... ... ... ... ... ... ... ... ... ... ... .15
II СИМПЛЕКС КЕСТЕ ЖОЛДАРЫ МАҚСАТТЫ ФУНКЦИЯНЫҢ КОЭФФИЦИЕНТТІҢ ИНДЕКСІН ШЫҒАРУ 21
2.1 Бірінші симплекс кестесі 22
ҚОРЫТЫНДЫ 23
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 23

Электронды есептеуіш машинаның шығуымен байланысты жаңа ғылыми-техникалық революция ғылымның жаңа даму бағытын орнатты. Осындай бағыттардың бірі – операцияны зерттеу ғылымы.
Операция дегеніміз – белгілі мақсатқа жеткізетін және нақты ниетпен біріктірілген шаралар жиынтығы. Операциялар: басқарылатын және басқарылмайтын болады.
Операцияны зерттеу дегеніміз – автоматтандырылған басқару жүйесіндегі басқару есептерін шешуге қолданатын ғылыми тәсіл. Операцияны зерттеу методологиясы негізгі мына топтарға бөлінеді:
- анықтамалар, кезеңдер, принциптер, есептер;
- операцияны зерттеудің математикалық әдістері. Оған сызықтық бағдарламалау, транспорттық, дискреттік бағдарламалау, бейсызықтық бағдарламалау, динамикалық бағдарламалау, ойындар теориясы кіреді;
- АБЖ жобалау кезіндегі операцияларды зерттеудің әдістерін қолдану. Онда АБЖ-ң алгоритмін қамтамасыз ету, информациямен АБЖ-ны қамтамасыз ету, техникалық қамтамасыз ету керек.
Сызықтық программалау, практикаға маңызды сызықтық функцияның, сызықтық теңсіздіктер немесе теңдеулер түріндегі шектеулердің бар болу кезіндегі максимумын (минимумын) табу, экстремумдық есептерді шешудің классикалық әдістері қажет болмай қалған есебін зерттейді.
Қазіргі уақытқа дейін сызықтық программалаудың ең қарапайым есептерінің бірі, кең тарағаны – транспорттық есеп. Яғни, жүктердің жіберу пункттерінен олардың бару пункттеріне біріктірудің, жүкті тасымалдаудың шығын бағасы минимиза-цияланатын есеп. Оны шешу үшін сызықтық программалау есептерінің барлығына ортақ симплекс әдісінен кішірек болатын сызықтық программалаудың арнайы әдістері қолданылады. Транспорттық есепті шешудің ең танымал әдістеріне потен-циал, солтүстік-батыс, минимал элемент әдістері жатады.

1. Үстенова О, Нүсіпбеков С. Экономикалық жүйелерді модельдеудің математикалық әдістері – Астана, Фолиант баспасы, 2010 жыл.
2. Акулич И.Л. Математическое программирование в примерах и задачах. – М. Высшая школа 1986.
3. Власов М.П., Шимко П.Д. Моделирование экономических процессов. – -Ростов-на-Дону, Феникс, 2005.
4. Алесинская Т.В. Экономика – математические методы и модели. Таганрог 2002.
5. Житников С.А., Биржанова З.Н., Аширбеков Б.М. Экономика – математические методы и модели: Ученое пособие. – Караганда, издательство КЭУ, 1998.
6. Ә.Ж. Сапарбаев, Қ.А. Ахметов, А.Т. Мақұлова. Экономикалық – математикалық әдістер мен модельдер. Алматы: Қазақстан жоғары оқу орындарының қауымдастығы, 2005 жыл.
7. Беркінбаев К. М, Ажиханов Н. Т, Нұрыллаев А. М., Ниязова Г. Ж.. «Компьютерлік модельдеу негіздіері» (Оқу әдістемелік құрал) - Алматы, 2005 жыл.
8. Васильков Ю.В, Василькова Н. Н. «Компьютерный технологии вычислительний в математическом моделировании» уч. Пособие.- М:1999.
9. Горчанов А. А, Орлова И. В. «Компьютерные экономико – математическое модели» - М: Компьютер, ЮНИТИ, 1995.
10. Оспанов С. С, Асқарова Ж.А. « Экономикадағы сызықтық модельдерді талдаудың математикалық әдістері» (оқу - әдістемелік құрал) – Алматы, 2006 жыл.

Пән: Экономика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министірлігі
Рымбек Байсеитов атындағы Семей қаржы-экономикалық колледжі РМҚК

Курстық жұмыс
Пән: Өндірістік және экономикалық үрдісін модельдеу

Тақырыбы: Транспорттық тапсырма

Дайындаған:
3 негізгі ВТ - 2 тобының оқушысы Жомартов Алмас
Тексерген:
Қорғаған бағасы:_______

2016 - 2017 оқу жылы
МАЗМҰНЫ

КІРІСПЕ 3
I ТРАНСПОРТТЫҚ ТАПСЫРМА 4
1.1 Транспорттық есеп. 4
1.2 Транспорттық модельдерді шешу әдістеріне қысқаша шолу 8
1.3 Транспорттық есепті желілік әдіспен шешу ... ... ... ... ... ... ... ... ... ... ... ... ..12
1.4 Транспорттық есептің математикалық моделі ... ... ... ... ... ... ... . ... ... ... ... 15
II СИМПЛЕКС КЕСТЕ ЖОЛДАРЫ МАҚСАТТЫ ФУНКЦИЯНЫҢ КОЭФФИЦИЕНТТІҢ ИНДЕКСІН ШЫҒАРУ 21
2.1 Бірінші симплекс кестесі 22
ҚОРЫТЫНДЫ 23
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 23

КІРІСПЕ

Электронды есептеуіш машинаның шығуымен байланысты жаңа ғылыми-техникалық революция ғылымның жаңа даму бағытын орнатты. Осындай бағыттардың бірі - операцияны зерттеу ғылымы.
Операция дегеніміз - белгілі мақсатқа жеткізетін және нақты ниетпен біріктірілген шаралар жиынтығы. Операциялар: басқарылатын және басқарылмайтын болады.
Операцияны зерттеу дегеніміз - автоматтандырылған басқару жүйесіндегі басқару есептерін шешуге қолданатын ғылыми тәсіл. Операцияны зерттеу методологиясы негізгі мына топтарға бөлінеді:
- анықтамалар, кезеңдер, принциптер, есептер;
- операцияны зерттеудің математикалық әдістері. Оған сызықтық бағдарламалау, транспорттық, дискреттік бағдарламалау, бейсызықтық бағдарламалау, динамикалық бағдарламалау, ойындар теориясы кіреді;
- АБЖ жобалау кезіндегі операцияларды зерттеудің әдістерін қолдану. Онда АБЖ-ң алгоритмін қамтамасыз ету, информациямен АБЖ-ны қамтамасыз ету, техникалық қамтамасыз ету керек.
Сызықтық программалау, практикаға маңызды сызықтық функцияның, сызықтық теңсіздіктер немесе теңдеулер түріндегі шектеулердің бар болу кезіндегі максимумын (минимумын) табу, экстремумдық есептерді шешудің классикалық әдістері қажет болмай қалған есебін зерттейді.
Қазіргі уақытқа дейін сызықтық программалаудың ең қарапайым есептерінің бірі, кең тарағаны - транспорттық есеп. Яғни, жүктердің жіберу пункттерінен олардың бару пункттеріне біріктірудің, жүкті тасымалдаудың шығын бағасы минимиза-цияланатын есеп. Оны шешу үшін сызықтық программалау есептерінің барлығына ортақ симплекс әдісінен кішірек болатын сызықтық программалаудың арнайы әдістері қолданылады. Транспорттық есепті шешудің ең танымал әдістеріне потен-циал, солтүстік-батыс, минимал элемент әдістері жатады.

I ТРАНСПОРТТЫҚ ТАПСЫРМА

0.1 Транспорттық есеп

Транспорттық есеп - сызықтық программалау есебінің тәжі-рибеде ең көп тарағандарының бірі. Кейде оны тасымалдау есебі деп те айтады. Тек жүкті тасу қарастырылған есеп болған жағдайда есепті осылай атау орынды да. Оның негізгі мақсаты тауарларды тиімді және ұтымды тасымалдау жоспарын құру болса, тәжірибеде осы есептің математикалық аппараттарына және шығару алгоритм-деріне сәйкес келетін жүк тасмалдаудан басқа мақсаттағы есептер-дің түрлері көптеп кездеседі. Сондықтан, мұндай есептер халық шаруашылығында маңызды есептердің қатарына жатады және ол-ардың барлығын транспорттық типтес есептер деп атайды.
Транспорттық есептердің тәжірибелік маңызын терең қарас-тырмастан бұрын қарапайым есептердің алғашқы қойылуын және есепті формалдау ретін талқылайық. Бірінші кезекте транспорттық есептердің жалпы математикалық моделін жазу үшін төмендегідей шартты белгілерді және атауларды қабылдайық.
Жалпы бір тектес өндірілген (шығарылған) өнімді, бір тектес жүк деп, өнім өндіретін орындарды жүк жіберетін пункттер, ал өнім қабылдайтын орындарды тұтынушы пункттер деп атайық. Негізінде мұндай атаулар жуықтап алынған және шартты түрде есептің қойылу мағынасы түсінікті болу үшін қабылданған. Өйткені тәжірибеде халық шаруашылығында, оның ішінде ауыл шаруа-шылығында транспорттық есептің математикалық аппаратын қол-дануға болатын, бірақ мағынасы тіптен ұқсамайтын есептер көптеп кездеседі.
Айталық, жүк жіберетін пункттердің санын - m (олардың нөмірлер индексін j-десек, онда j =1,2,... m), ал тұтынушылардың санын - n (олардың нөмірлер индексін і-десек, онда і=1,2,... n) деп белгілейік.
Әрбір жүк жіберетін пункттерді нөмірлеріне сәйкес (A1, A2,...Am), ал тұтынушыларды нөмірлеріне сәйкес (B1, B2,...Bn) деп атайық. Жүк жіберетін пункттерде өндірілген өнімдер көлемі (а1, а2, ...аm) және олардың тұтынушыларға керекті мөлшері (b1, b2, ...bn) жүк көлемдеріндей болсын.
Cіj - і-ші тұтынушыға j-ші жүк жіберетін пункттен жүкті тасығанда, оның бір өлшем бірлігіне есептеген шығын (мұндағы і=1,2,...n; j =1,2,...m), яғни С11, С12, ...Сnm. Бұл көрсеткіш әртүрлі мағынада болуы мүмкін: ақша шығыны, уақыт, еңбек өнімділігі, арақашықтығы және т.б.с.с. Әдебиеттерде бұл көрсет-кішті тасымалдаудың ²Тарифы² немесе кестеге жазылғаннан кейін і-ші жолмен j-ші бағананың қиылысында тұрған тордың бағасы деп атайды.
хіj - і-ші тұтынушыға j-ші жүк жіберетін пункттен таситын жүктің оңтайлы мөлшері, яғни таситын жүк көлемі белгісіз (х11, х12, ...хnm ).
Тұрғызылатын математикалық модельдің мағынасы түсінікті болу үшін көмекші кесте тұрғызайық (3.1-кесте).
3.1-кесте
№1
A1
A2
...
Am
Жүкке сұран.
B1
х11 С11
х12 С12
...
х1m С1m
b1
B2
х21 С21
х22 С22
...
х2m С2m
b2
. . .
. . .
. . .
. . .
. . .
. . .
Bn
хn1 Сn1
хn2 Сn2
...
хnm Сnm
bn
Жүк мөлшері
a1
a2
...
am
-

Есептің мақсаты әрбір жүк жіберетін пункттен барлық тұ-тынушыларға тиісті мөлшерде жүкті аз шығынмен тасымалдау жоспарын құру, олай болса барлық шығын:
Z=C11х11 +C12х12+...+ Cnmхnm -- mіn (3.1)
Мына жағдайда:
а) барлық жүк жіберетін пункттерден тасымалдауға арналған жүк көлемдері толығымен тиісті орындарына жеткізілінеді, олай болса:
х11 + х21+...+ хn1 = a1
х12 + х22 +...+хn2= a2
... ... ...
х1m + х2m +...+хnm= am (3.2)
б) жүк әрбір тұтынушыға керекті мөлшерде тасылуы керек:
х11 + х12 + ...+ х1m = b1 х21 + х22 + ...+ х2m = b2 . . . . . . . . .
хn1 + хn2 + ...+ хnm = bn (3.3)
в) әрбір жүк жіберетін пункттен әр тұтынушыға таситын жүктің мөлшері теріс сан болуы мүмкін емес (яғни хіj0 - жүк тасу тиімді немесе хіj=0 - жүк тасу тиімсіз):
х11 ³ 0, х12 ³ 0,... хnm ³ 0. (3.4)
Сонымен (3.1) ... (3.4) жалпы транспорттық есептің кеңейтіл-ген моделі болып есептелінеді.
- сома белгісі арқылы транспорттық есептің математи-калық моделін құрама түрінде көрсетейік:
(3.5)
Шектеу шарттары:
(3.6)
(3.7)
хіj=0, (3.8)
Мына жағдайда:
(3.9)
яғни барлық жүк жіберілетін пункттерде өндірілген немесе жинал-ған жүктің көлемі толығымен тұтынушылардың сұраныстарын қамтамасыздандырады. Мұндай транспорттық есеп жабық немесе балансталған деп аталады.
Егер математикалық модельде шарты орындалмаса, мұндай транспорттық (тасымалдау) есептерінің моделін ашық немесе балансталмаған модель деп атайды.
Транспорттық есептің моделі ашық болған жағдайда есепті шешу үшін оны жабық транспорттық есепке айналдырады.
Егер болса, онда жүк артық жиналған, мұндай жағдайда есепті жабу үшін жалған тұтынушы (Bn+1) енгізіледі де, оның жүкке сұраныс мөлшерін мына қатынаспен есептейді:
bn+1=Σaj - Σbі.
Кейбір әдебиеттерде мұндай есептер Артығымен тасымал-дау есебі немесе Балансталмаған, ашық транспортық есеп делінеді.
Егер болса, онда өндірілген өнім (жүк) мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтамасыз ет-пейді, мұндай жағдайда есепті жабу үшін жалған жүк жіберуші пункт (Аm+1) енгізіледі де, ондағы жиналған жүк мөлшерін мына қатынаспен есептейді:
аm+1=Σbі - Σaj.
Жүктің бір бірлігін тасуға кететін шығын (жалған тордың бағасы), яғни бірінші жағдайда: Cn+1,1= 0, Cn+1,2= 0,...,Сn+1,m= 0, ал екінші жағдайда: C1,m+1 = 0, C2,n+1= 0,...,Сn,m+1= 0-деп алынады.
Қарастырылып отырған тақырыпта жоғарыдағы келтірілген транспорттық есептердің математикалық модельдері аграрлық өн-еркәсіп кешенінің көптеген есептерінің математикалық аппарат-тарының негізін құрайтынын атап өттік. Мысалға, ауыл шаруа-шылығында ауыспалы егістік жерлерді оңтайлы жоспарлауда, техниканы әртүрлі жұмысқа оңтайлы бөлуде, өндіріс мамандарын әртүрлі жұмысқа тиімді бекітуде, өндіріс орындарын тиімді түрде орналастыруда, тағы басқа да көптеген есептерде қолданылады.

0.2 Транспорттық модельдерді шешу әдістеріне қысқаша шолу

Жалпы транспорттық есеп сызықты программалау есебінің құрамына енеді. Дегенмен де, сызықты программалау есептерін ше-шуге арналған компьютерлік программалар пакеттері дамығанға дейін, транспорттық есепті симплекстік әдіспен шешуде, қосымша іс-әрекеттер жүргізуді қажет ететін біраз ерекшеліктер кездеседі. Жоғарыда қарастырылған сызықты программалау есептерінің математикалық моделінде белгісіз х-тер тек бір ғана j = 1,2,...n индекспен берілген. Ал тасымалдау (транспорттық) есебінде белгі-сіздер екі индекспен анықталады.
Транспорттық есепті симплекс әдісімен шешкен кезде екі индексті (өлшемді) көрсеткіштер бір индексті көрсеткіштерге ауыстырылады, мысалы:
х11= у1, х12= у2, х13= у3, х14= у4, х21= у5, х22= у6, және т.б.с.с.
с11= v1, c12= v2, c13= v3, c14= v4, c21= v5, c22= v6, және т.б.с.с.
Осы әрекеттердің нәтижесінде транспорттық есептің матема-тикалық моделі жоғарыдағы баяндалған сызықтық программалау есебінің симплекс әдісімен шығарылатын түріне ауысады. Сөйтіп, есепті шығару үшін симплекс әдісін қолдануға болады. Бірақ, есеп-тің шарты қарапайым, ал ізделінетін белгісіздер өте көп және есепті ешқандай есептеу техникасынсыз қолмен симплекс әдісін қолда-нып шығару өте ыңғайсыз.
Осы келтірілген жағдайларға байланысты ғалымдар транс-порттық есепті шығарудың симплекс әдісінен басқа жолын қарас-тырды. Қазіргі кезде транспорттық есептерді шығаруға өте ыңғай-лы көптеген әдістер жасалынған. Мысалға, үлестіру (тарату) әдісі, Венгер әдісі, потенциал әдісі, Вогель (Фогель) әдісі және тағы басқа әдістер тәжірибеде кеңінен таралған. Солардың ішінен 1949 жылы Кеңестер Одағының белгілі математигі, академик Л.В. Кантарович және М.К. Гавурин ұсынған тарату (үлестіру) әдісі тәжірибеде кеңінен қолданылады.
Транспорттық есептерді шешуге арналған әдістердің көпші-лігі осы есептердің математикалық моделінің мына қасиеттеріне сүйенеді:
- барлық шектеуші шарттар тек теңдік түрінде беріледі;
- әрбір белгісіз тек екі-ақ теңдеудің құрамына енеді;
- шектеуші шарттардағы белгісіздердің коэффициенттері бірге тең.
Транспорттық есептерді шешуге арналған барлық әдістерді қолданғанда есепті шешу әрқашанда тірек жоспарын құрудан басталады (бірінші құрылған кестені базистік шешім деп атайды). Математикалық программалау пәніне арналған әдебиеттерде [12, 13, 15, 16...] тірек жоспарын құрудың бірнеше тәсілдерін кездестіруге болады. Солардың ішінде ең көп кездесетіндері:
n солтүстік - батыс бұрышы ережесі;
n екі есе ұтымды ережесі;
n жол немесе бағана бойынша ең кіші элемент ережесі;
n матрица кестесіндегі ең кіші элемент ережесі;
n Вогель (Фогель) әдісі.
Осы ережелердің бірімен тірек жоспарын құрғанда әрқашан-да толтырылған торлардың саны мына талапқа дәл болуға тиіс:
Kт = m + n - 1,
бұл жағдай үлестіру әдісінің бірінші талабы.
Үлестіру (тарату) әдісі. Транспорттық есепті шешуге арнал-ған және тірек жоспарын біртіндеп жақсарту ретін нақтылы көрсе-тіп бейнелейтін ең бірінші жасалған әдіс. Ол осы әдістің негізінде жасалынған МОДИ әдісін (модификацияланған) оқып үйренуге жақсы кіріспе болып табылады.
Бірінші кезекте жоғарыда көрсетілген ережелердің бірімен тірек жоспары құрылады. Барлық бос торлар үшінарнайы тәртіп-пен және ереже бойынша тұйықциклдар тұрғызылады.
Бос торлардың сипаттамалары мына формуламен есептелі-неді:

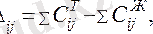
мұндағы - циклдың тақ торларының бағалары (бос тор бірінші тақ тор болып есептелінеді де, әрі қарай жұп, келесісі тақ болып әрі қарай цикл бойынша қайталана береді. Есептеу кез келген бағытта немесе цикл бағытымен жүргізіледі);
- циклдың жұп торларының бағалары.
Оңтайлы жағдайдың белгісін тексеру. Егер Z (R) mіn, онда барлық бос торлардың сипаттамасы оң сан болса, яғни: , базистік шешім оңтайлы делінеді. Егер Z (R) max, онда барлық бос торлардың сипаттамасы теріс сан болса, яғни: , базистік шешім оңтайлы делінеді.
Егер құрылған жоспар оңтайлы емес және бірнеше теріс сипаттама болса, онда осы сипаттамалардың ең кішісі бойынша цикл құрылады да, түрлендіру жүргізіледі, яғни бір рет орнын ауыстыру әрекеті жасалынады [12, 13, 15].
МОДИ әдісі (потенциалдар әдісі).Үлкен өлшемді кестелерде транспорттық есептерді үлестіру (тарату) әдісімен циклдер құрып сипаттамаларды есептеу, өте ыңғайсыз. Осындай есептерді моди-фикацияланған тарату әдісімен (МОДИ) шешкенде есептеу технологиясы көп жеңілденеді. Цикл құрмай-ақ бос торлардың сипаттамаларын мынадай формуламен есептеуге болады:
Dіj = Cіj - (Uі + Vj ),
мұндағы Cіj - бос торлардың бағасы;
Uі - кестенің і-жолының потенциалы;
Vj - кестенің j - бағанасының потенциалы.
Негізінде МОДИ әдісі үлестіру (тарату) әдісімен сәйкес, ал потенциалдар әдісінен айырмашылығы бос тордың сипаттамасын анықтайтын формуланың таңбасы әртүрлі.
Потенциал деп мына формуламен: Cіjт = Uі+Vj немесе кейбір әдебиеттерде Cіjт =αі+βj есептелген кез келген сандар жұйелерін айтады. Мұндағы Сіjт - толтырылған (базистік) тордың бағасы; Uі сияқты αі - кестенің і-жолының потенциалы; Vj сияқты βj - кестенің j - бағанасының потенциалы.
МОДИ әдісі бойынша бірінші кезектеалғашқы тіректік шешім жоғарыдағы айтылған ережелердің бірімен құрылғаннан кейін жоғарыда келтірілген формула (Cіjт =Uі+Vj) бойынша базистік (толтырылған) тордың жолының-Uі және бағанасының-Vj потен-циалдары анықталынады. Бірінші жолдың потенциалы U1 = 0-ге тең деп алынады. Бос торлардың сипаттамаларын мына формула-мен есептейді: Dіj = Cіj - (Uі + Vj ). Келесі жасалатын әрекеттер үлестіру (тарату) әдісімен бірдей.
Дифференциалдық ренталар әдісі. Егер потенциалдар әдісі-мен транспорттық есептің оңтайлы жоспарын анықтау үшін ең бірінші оның тірек жоспарын құрып, одан кейін ол біртіндеп жақ-сартылса, ал дифференциалдық ренталар әдісімен ең бірінші тасымалданатын жүктің негізгі бөлігі ең тиімді түрде бөлінеді де (мұндай әрекет шартты-оңтайлы бөлу делінеді), осыдан кейін келесі итерацияларда (әрекеттерді қайтадан қайталау) жүктің бө-лінбей қалған бөліктері біртіндеп бөлініп, аяғында тиімді оңтайлы жоспар құрылады.
Венгер әдісі.Бұл әдістің негізгі идеясы: жол (бағана) бірдей шамаға dj (dі) өзгергенде (көбейсе немесе кемісе) есептің оңтайлы жағдайы ешқандай өзгеріске ұшырамайды.
Қазіргі кезде тірек жоспарын құрғанда бірден немесе оңтайлы шешімге өте жақын базистік шешімді құруға мүмкіндік беретін бірнеше әдістер белгілі. Солардың бірі аппроксимация (аппроксимация ағылшын сөзі - ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.