Векторлар және олардың есептер шығаруда қолданылуы

МАЗМҰНЫ

КІРІСПЕ 3

1. ВЕКТОР ҰҒЫМЫНЫҢ ТЕОРИЯЛЫҚ СИПАТТАЛУЫ 6
1.1 Вектор ұғымы және оның шығу тарихы 6
1.2 Векторларға амалдар қолдану 11
1.3 Векторларды жіктеу тәсілдері 23

2 ВЕКТОРЛАРДЫ ЕСЕПТЕР ШЫҒАРУДА ҚОЛДАНУ 26
2.1 Алгебраның кейбір есептерін шығаруда векторды қолдану 26
2.2 Планиметрияның кейбір есептерін шығаруға векторды қолдану 34

ҚОРЫТЫНДЫ 52

ӘДЕБИЕТТЕР ТІЗІМІ 54

ҚОСЫМША А 57

ҚОСЫМША Ә 59

КІРІСПЕ

Қоғамдағы қазіргі кездегі қайта құрулар, экономиканы дамытудағы жаңа стратегиялық бағдарлар, қоғамның ашықтығы, оның жедел ақпараттануы мен қарқынды дамуы білім беруге қойылатын талаптарды түбегейлі өзгертті.
Әлемнің жетекші елдерінің көпшілігінің білім беру, білім берудің мақсатын, мазмұны мен технологияларын оның нәтижесіне қарап бағалайтын болды.
Жас ұрпақты жан-жақты жетілген, ақыл-парасаты, өресі биік, өз Отанын сүйетін азамат етіп тәрбиелеудегі басты тұлға – ұстаз. Қазіргі таңда жемісті еңбегімізбен шығармашылық ізденісіміз арқылы ғана реалды жаңару жолына шыға аламыз.
Математиканы оқытудағы негізгі міндет – математикалық білім, білік жүйелерін нақты және сапалы меңгеруді қамтамасыз ету қабілеттерін дамыту мен анықтау т.с.с.
Тәуелсіз Қазақстанымыздың экономикасы өркендеп, өндіріс орындарыныың жандануына байланысты математика, физика-техника салаларының ғалымдарына, білікті мамандарына деген сұраныс, қазіргі кезеңде, күрт артып отыр.
Елімізге қажет болып отырған мамандарды бүгінгі күні мектеп партасында отырған математика, физика пәндеріне бейімділік танытқан оқушылардан тәрбиелеп, өсіріп шығаруға болатыны түсінікті. Бұл тұрғыда математика бағытында білім беріп жатқан мектептер мен сыныптардың маңызы ерекше. Өйткені, олардың түлектерінің басым көпшілігі өз білімдерін жоғарғы оқу орындарында математика, техника салалары бойынша жалғастыратыны белгілі.
Біздің жоғары оқу орындарымыздың физика-математика және техника салалары бойынша мамандар дайындайтын факультеттерінің талапты да талантты студенттерінің бірқатары математикадан тереңдете білім беретін, аталмыш сыныптардың түлектері. Сондықтан, математика бағытында білім беріп жатқан сыныптарға тиісті көңіл бөлу – уақыт талабы.
Бұл тұрғыда оқушыларға мектепте оқытылатын математика салаларын, соның ішінде, техникалық ғылымдардың негізі болып табылатын векторлар ұғымы неғұрлым тереңірек білгізіп, меңгерту керек.
Ғылымның бұл саласын дамытуға үлес қосқандар қатарына К.Вексель (1745-1818), К.Гаусс (1777-1855), Л.Лоуренс (1901-1958) т.с.с. ғалымдарды атауға болады.
Осыған орай біз өз бітіру зерттеу жұмысымыздың тақырыбын «Векторлар және олардың есептер шығаруда қолданылуы» деп алуды жөн көрдік.
Мектеп математика курсында векторлар тақырыбына 15 сағат берілген. 10 сағат теория, 5 сағат практикаға берілген.
Зерттеудің мақсаты: негізгі мектепте математика курсындағы есептерді шығаруда векторларды қолдану ерекшеліктері мен тиімділігін анықтау.
Зерттеудің объектісі: оқушы танымын жетілдіретін оқу үрдісі.
Зерттеудің пәні: негізгі мектепте математика курсында есеп шығаруда танылатын оқушы іс-әрекеті.
Зерттеудің болжамы: егер математика курсында геометриялық есептерді шығаруда оқушылар векторлық әдісті жете меңгерсе, онда олардың математикалық білім, білік дағдылары жетіле түсер еді.
Зерттеудің мақсаты мен болжамына сәйкес төмендегідей міндеттер туындайды:
1. математика курсында оқытылатын векторлар ұғымының шығу тарихына шолу жасау.
2. векторлар ұғымы туралы негізгі түсініктердің мәнін ашу.
3. вектордың түрлеріне тоқталу.
4. векторларға қолданылатын негізгі амалдарды көрсету.

ӘДЕБИЕТТЕР ТІЗІМІ

1. Алимов Ш.А. Алгебра и начала анализа. Учебник для 10-11 классов, средняя школа, М, Просвещение, 1992
2. Атанасян Л.С. и другие. Геометрия для 9-10 классов средней школы.М, Просвещение, 1994.
3. Колмогоров А.И. Агебра и начала анализа. М, Просвещение, 1994.
4. Галицкий Углубленное изучение алгебры и начала анализа. М, П, 1997.
5. Гусев В.А.,Мативненко В.И. Практика по элементарной математике. М, Просвещение, 1991.
6. 3000 конкурсных задач по математике. М, Айриа пресс, 1999.
7. Зив Б.Р., Гольдич В.А. Дидактические материалы по алгебре и начала анализа для 9-10 класов, С-П, 2000.
8. Қаңлыбаев Қ. Жазықтықты векторларда қолданылатын есептер., математика, №2, 11 бет.
9. Жақсыбекова К.А. Векторлық және тензорлық оқу құрал. Алматы, Қазақ университеті, 2003, 104 бет.
10. И.Қазиев Решение алгебрических задач с помощью скалярного произведения, Математика в школе, журнал, 17 стр, №4
11. И.М.Фихтенгольц Математикалық анализ негіздері, Мектеп, Алматы, 1972 жыл, 75 бет.
12. Т.Ахметқалиев Математикалық талдау, Алматы, 1997 жыл, 262 бет.
13. А.П. Ершова Самостоятельная работа по геометрии и алгебры. Москва «Илекса!, 2000, 172 бет.
14. Б.Т. з и в, Дидактические материалы геометрий. Москва, 98, 70 бет.
15. Бүкібаева К. Векторларды есептерді шығаруда қолдану, журнал, ИФМ 27 бет, №4, 1993 жыл.
Қ.Р. Білім туралы заң баптары бойынша түсінік негіздері, 75 бет.
16. М.Асқарова Векторлар және оларға амалдар қолдану.Алматы.1992 жыл 123 бет.
17. Аяпбергенова С. Аналитикалық геоетрия Алматы,1971 жыл.
18. Әмірбаев М Аналитикалықгеометрия 1.2 бөлімдері, Алматы,1963-1966жыл.
19. Жәутіков О.А. Матаматикалық анализ Алматы,1961 жыл 45 бет.
20. Ибраикулов Ә.М Жоғарғы математикадан жаттығулар мен өзінді тапсырмалар Алматы,ҚАЗҰТУ 200 жыл 132 бет.
21. Ибрашев Х.И, Еркеғұлов Ш.Т. Математикалық анализ курсы 1.2-том Алматывы,1963-1970 жыл.
22. Клетеник Д .В. Сборник задач по аналитической геометрий. Москва :наука,1983-244 бет.
23. Хасеинов К.А. Математика канондары Алматы,2004-56бет.
24. Глейзер Н.С Ұлы матеатика курсы Алматы 1995 жыл.
25. Бекер Б.Н. Применеие векторов Москва,Шкоа пресс-120 стр.
26. Тасболатов Р.М Планиметрия есептері Алматы,Ы.Алтынсарин атындағы білім ордасы,2000 жыл 133-бет.
27. Просолов В.В. Задачи планиетрий Москва, Наука 1986 год, 1-часть 37стр, 2-часть1991 год 240 бет.
28. Гусятиков В,Г. Векторая алгебра в примерах и задачах. Москва, Высшая школа 1985 год,232 стр.
29. Колмагоров А.Э Матеатик все историй рзвития Москв,ук 1991 год 204стр.
30. Ермалаева .Н.А. Новые курсы математики средей школы. Москва,Просвещеия 1985 год.
Погорелов А.В ГЕометрия 7-11 сыып Алматы, Рауа, 1997-384

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 56 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ

БІТІРУ ЖҰМЫСЫ

Тақырыбы: ВЕКТОРЛАР ЖӘНЕ ОЛАРДЫҢ ЕСЕПТЕР ШЫҒАРУДА ҚОЛДАНЫЛУЫ

МАЗМҰНЫ

КІРІСПЕ 3
1. ВЕКТОР ҰҒЫМЫНЫҢ ТЕОРИЯЛЫҚ СИПАТТАЛУЫ 6
1.1 Вектор ұғымы және оның шығу тарихы 6
1.2 Векторларға амалдар қолдану 11
1.3 Векторларды жіктеу тәсілдері 23
2 ВЕКТОРЛАРДЫ ЕСЕПТЕР ШЫҒАРУДА ҚОЛДАНУ 26
2.1 Алгебраның кейбір есептерін шығаруда векторды қолдану 26
2.2 Планиметрияның кейбір есептерін шығаруға векторды қолдану 34
ҚОРЫТЫНДЫ 52
ӘДЕБИЕТТЕР ТІЗІМІ 54
ҚОСЫМША А 57
ҚОСЫМША Ә 59

КІРІСПЕ

Қоғамдағы қазіргі кездегі қайта құрулар, экономиканы дамытудағы жаңа
стратегиялық бағдарлар, қоғамның ашықтығы, оның жедел ақпараттануы мен
қарқынды дамуы білім беруге қойылатын талаптарды түбегейлі өзгертті.
Әлемнің жетекші елдерінің көпшілігінің білім беру, білім берудің
мақсатын, мазмұны мен технологияларын оның нәтижесіне қарап бағалайтын
болды.
Жас ұрпақты жан-жақты жетілген, ақыл-парасаты, өресі биік, өз Отанын
сүйетін азамат етіп тәрбиелеудегі басты тұлға – ұстаз. Қазіргі таңда
жемісті еңбегімізбен шығармашылық ізденісіміз арқылы ғана реалды жаңару
жолына шыға аламыз.
Математиканы оқытудағы негізгі міндет – математикалық білім, білік
жүйелерін нақты және сапалы меңгеруді қамтамасыз ету қабілеттерін дамыту
мен анықтау т.с.с.
Тәуелсіз Қазақстанымыздың экономикасы өркендеп, өндіріс орындарыныың
жандануына байланысты математика, физика-техника салаларының ғалымдарына,
білікті мамандарына деген сұраныс, қазіргі кезеңде, күрт артып отыр.
Елімізге қажет болып отырған мамандарды бүгінгі күні мектеп
партасында отырған математика, физика пәндеріне бейімділік танытқан
оқушылардан тәрбиелеп, өсіріп шығаруға болатыны түсінікті. Бұл тұрғыда
математика бағытында білім беріп жатқан мектептер мен сыныптардың маңызы
ерекше. Өйткені, олардың түлектерінің басым көпшілігі өз білімдерін жоғарғы
оқу орындарында математика, техника салалары бойынша жалғастыратыны
белгілі.
Біздің жоғары оқу орындарымыздың физика-математика және техника
салалары бойынша мамандар дайындайтын факультеттерінің талапты да талантты
студенттерінің бірқатары математикадан тереңдете білім беретін, аталмыш
сыныптардың түлектері. Сондықтан, математика бағытында білім беріп жатқан
сыныптарға тиісті көңіл бөлу – уақыт талабы.
Бұл тұрғыда оқушыларға мектепте оқытылатын математика салаларын,
соның ішінде, техникалық ғылымдардың негізі болып табылатын векторлар ұғымы
неғұрлым тереңірек білгізіп, меңгерту керек.
Ғылымның бұл саласын дамытуға үлес қосқандар қатарына К.Вексель (1745-
1818), К.Гаусс (1777-1855), Л.Лоуренс (1901-1958) т.с.с. ғалымдарды атауға
болады.
Осыған орай біз өз бітіру зерттеу жұмысымыздың тақырыбын Векторлар
және олардың есептер шығаруда қолданылуы деп алуды жөн көрдік.
Мектеп математика курсында векторлар тақырыбына 15 сағат берілген. 10
сағат теория, 5 сағат практикаға берілген.
Зерттеудің мақсаты: негізгі мектепте математика курсындағы есептерді
шығаруда векторларды қолдану ерекшеліктері мен тиімділігін анықтау.
Зерттеудің объектісі: оқушы танымын жетілдіретін оқу үрдісі.
Зерттеудің пәні: негізгі мектепте математика курсында есеп шығаруда
танылатын оқушы іс-әрекеті.
Зерттеудің болжамы: егер математика курсында геометриялық есептерді
шығаруда оқушылар векторлық әдісті жете меңгерсе, онда олардың
математикалық білім, білік дағдылары жетіле түсер еді.
Зерттеудің мақсаты мен болжамына сәйкес төмендегідей міндеттер
туындайды:
1. математика курсында оқытылатын векторлар ұғымының шығу тарихына
шолу жасау.
2. векторлар ұғымы туралы негізгі түсініктердің мәнін ашу.
3. вектордың түрлеріне тоқталу.
4. векторларға қолданылатын негізгі амалдарды көрсету.
5. негізгі мектеп математика курсындағы есептерді шығаруда
векторларды қолданудың тиімділігін көрсету.
Негізінен бітіру жұмысы кіріспеден, екі негізгі тараудан,
қорытындыдан, қолданылған әдебиеттер тізімінен және қосымшадан тұрады.
1. ВЕКТОР ҰҒЫМЫНЫҢ ТЕОРИЯЛЫҚ СИПАТТАЛУЫ

1.1 Вектор ұғымы және оның шығу тарихы

Қазіргі заман математикасының негізгі де ілгерлі ұғымдарының бірі –
векторлық кеңістік ұғымы. Бұл ұғым математканың сызықтық алгебра, сыөызқтық
программалау, функционалдық анализ және физиканың толып жатқан салаларында
қолданылады. Векторлар теориялық физикада, механикада, гидродинамикада,
аэродинамикада, потенциалдар теориясында, қолданбалы математикада, химияда,
экономикада табысты қолданыс тауып отыр.
Векторлық аппарат қазіргі заман математикасында қолданумен шектелмей,
жоғары оқу орындарында оқытылатын техникалық, математикалық пәндердің
оқулықтарында лайықты орын алды. Векеторлық аппаатың атқаратын ролінің
маңыздылығы соншалық – аталмыш курстар векторлардың өздеріне қажетті
тарауларын толығымен қамтиды. Дифференциалдық геометрия, аналитикалық
геометрия, математикалық физика, теорялық физика векторлар негізінде
баяндалады.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық аппарат
көмегімен шешіледі. Компьютерді дифференциалдық геометрия, аналитикалық
геометрия, математикалық физика, теорялық физика векторлар негізінде
баяндалады.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық аппарат
көмегімен шешіледі. Компьютерді падаланып, дененің кескінін жасау үшін
векторлық графика пайдаланылады. Сызықтық программалауда вектордың
көмегімен толып жатқан практикалық мәселелер шешіледі. Мәселенки, өніріс
орнының ең тиімді жұмыс кестесін жасау, жүк тасымалдаудың ең пайдалы әдісін
іздеп, табу; матаны, қаңылтырды, тағы да сол сияқты заттарды кесіп-пішудің
үнемді әдісін табу – міне осы сияқты мәселелер. “Математикалық эконмика”
деп аталатын экономиканың саласында векторлардың көмегімен қарастырылады.
Қазіргі кезде өндіріс орнының қуатын вектор түрінде өрнектеу аса қолайлы
болып отыр. Векторлар қолдануларға өте бай.
Векторлық есептеулер математиканың жас салаларның бірі екендігіне
қарамастан, өзінің маңыздылығының арқасында, қолдану ауқымның кеңдігі
арқасында кейінгі елу – алпыс жыл шамасында көптеген елдерде мектеп
математикасына еніп, оның құрамдас бөлігі болып, орнығып алды.
Векторлар мектептерімізде оқытыла батағанына ширек ғасырдан артық
уақыт болды. Бірақ, мұғалімдерге қажетті тарихи-әдістемелік материалдар
әзірше дайындалмаған. Абстрактылығы жоғары векторларды оқушыларға саналы да
терең меңгерту үшін, олардың векторларды оқып-білуге деген ынтасын арттыру
үшін тарихимағлұматтар бере отырудың маңызды екендігі сөзсіз, Математика
пінінің мұғалімдері векторлық есептеулердің жасалу тарихын, векторлардың
қолдануларын, ғылым және техника салаларындағы маңызын білгендері абзал.
Жоғарыда айтылғандарды ескере келе, мұғалімдердің пайдалануына арнайы
дайындалған, векторлық есептеулердің жасалу тарихының қысқаша мазмұнын
төменде беріп отырмыз.
Техника ғылымдардың қауырт дамуына байланысты он сегізінші ғасырдың
өзінде-ақ есептеу аппаратын жетілдірудің қажет екендігі байқалды. Бұрыннан
қолданылып келегн есептеу түрлері ендігі жерде қажеттілікті қанағаттандыра
алмайтын болып шықты. Теориялық физиканың жедел де аса күшті қарқынмен
дамуына байланысты он тоғызыншы ғасырдың басныда математикалық аппаратты
жетілдіруге деген талап күшейе түсті. Есептеудің талапқа сай жаңа түрін
іздестіру қажет болды. Нәтижесінде он тоғызыншы ғасырдың екінші жартысында
веторлық есептеулер дүниеге келді де, үлкен қарқынмен тез дамыды және
математиканың құрамдас бір бөлігі болып қалыптасты.
Векторлық есептеулерді жасауға көптеген елдердің толып жатқан ғалым –
математикатері мен физика-механиктері, инженер-техниктері қыруар үлес
қосты. Векторлық есептеулердің жасы “жас” болғанымен бастау көзі сонау рете
заманда өмір сүрген данышпан Аристотельдің Механикалық проблемалар атты
еңбегінде табылды. Аристотель осы еңбегінде бір нүктеге түсірілген және де
өзара бұрыш жасай бағытталған екі күштің әсерінен дененің жүрген жолын
табуды екінші мәселе етіп қояды. Оның жиырма төртінші мәселесінің мазмұны
төмендегідей:
Ромбтың қабырғасының бойымен бірі-бірімен қарама-қарсы бағытта екі
нүкте бірдей жылдамдықпен қозғалып келеді. Ромбтың қабырғасы дәл сондай
жылдамдықпен қарсы жатқан қабырғаға қарай қозғалады.Әр нүктенің жүрген жолы
қандай?
Жауап: Әр нүкте ромб диаогналі бойымен қоғалады”.
Сұрақ: бірдей жылдамдықпен қозғалып келе жатқан нүктелер бірдей
уақытта неге әртүрлі жол жүреді?..
Міне осыдан Аристотельдің
- қозғалыстарды (орын ауыстыруларды) қосуға параллелограмм ережесін
қолданғандығы.
- векторлардың геометриялық қосындысн табудың қазіргі, біз қолданып
жүрген түріне өте жақын келгендігі анық байқалады.
Он жетінші ғасырда Аристотельдің “қозғалыстар параллелограмы”
қайтадан жанданды. Галилео Галилей (1564-1642) күш және оның денені
қозғайтын құраушысының арасындағы метрикалық байланысты зерттеді. Оның
еңбектеріне қарап, Галилейдің “теңәсерлі күш”, “қорытқы жылдамдық”
ұғымдарына өте жақын, қапталдас келгенін көруге болады. Ағылшын математигі,
әрі физигі атақты Исаак Ньютон (1643-1727) қозғалыстарды қосуға алғаш рет
“параллелограмм” ережесін пайдаланды. Неміс математигі Готфрид Вильгельм
Лейбниц (1646-1716) “геометриялық есептеулер” идеясын берді, оны әрі қарай
дамытпады.
Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис (1616-
1703) механикаға геометриялық аппарат жасап беруде жаңа әрі аса ірі қадам
жасады. Ол екі, үш күштің тең әсерлі және қорытқы күшін табуға, қорытқы
жылдамдықты табуға қолданылатын параллелограмм ережесін ғылымға алғаш
енгізген Джон Валлис болды. Күштерді, жылдамдықтарды қосу, жіктеу; векторды
санға көбейту амалдарын алғаш берген де осы адам. Сөйтіп , Джон Валлис
механикада векторлық алгебраның негізін қалаған оқымысты болды.
Он сегізінші ғасырда математика мен механикада аналитикалық
әдістерімен әуестенубасым болды. Леонард Эйлер (1707-1783) мен Лагранждың
арқасында механика математиканың жаң бір саласы болатын жағжайға
жеткізілді. Тек қана он сегізінші ғасырдың ақырғы кезінде Монждың (1746-
1816) геометрия мектебінде геометриялық әдістерге қайта оралуға деген
ұмтылыс байқалды. Әсіресе кинематикадағы қозғалыстарды зерттеуге
геометриялық әдіс аса тиімді болып шықты, Л. Карно бұл бағытта аса табысты
еңбек етті. Ол “Қозғалыстың геометриялық теориясын” жасау мәселесін
көтерді, векторды қосудың “көпбұрыш ережесін” және қазір пайдаланып жүрген
векторлық есептеудің символдық аппаратын жасап шықты.
Множ-Понселе мектебінің көрнекті өкілі Баре де Сен-Венан (1797-1886)
серпімділік теориясындағы, гидродинамикадағы, термодинамикадағы, жалпы
механикадағы тамаша еңбектерімен физиктер мен механиктер ортасында аса
танымал тұлға еді. Сен-Венан векторлық есептеулер саласында да қомақты үлес
қосты. Механикада қолданылатын векторлық аппаратты жетілдіруде жемісті
еңбек етті, векторлық аппаратты әрі қарай дамытты. “Об геометрических
суммах и разностях и их применение для упрощения механики” атты 1845 – жылы
жарияланған еңбегінде Сен-Венан скаляр көбейтінді, векторлық көбейтінді,
ветор функцияны дифференциялдау, интегралдау ережелерін берді. Сөйтіп, ол
механиканы вектор негізінде құрудың жалпы схемасын жасап шықты.
Понселенің шәкірті Резаль (1820-1896) 1862-жылы жарияланған “Чистая
кинематика” еңбегінде Сен-Венан жасаған векторлық апаратты жетілдіре түсті
және векторлық апараттың кинематикада қолдануларына толып жатқан мысалдар
көрсетті.
Векторлық есептеулердің негізін салушылар Ирландия математигі әрі
астрономы Уильям Гамильтон (1805-1865) және неміс математигі Герман
Грассман (1809-1877) деп айтылып жүр.
1844-жылы Уильям Гамильтонның векторлық есептеулерге арналған алғашқы
мақалалары және Герман Грассманның “Учение о протяженности” атты көлемді
еңбегі жарияланды. 1853-жылы Гамильтонның “Лекции о кватернионах” атты
еңбегі жарық көрді. Бұлардың әрқайсысы есептеудің жаңа әрі әмбебап түрін
жасамқшы болды, векторлық есептеулерге қыруар еңбек сіңірді. “Вектор
ұғымын” 1846-жылы ғылымға енгізген Гамильтон болды.
Векторлық есептеулердің негізін салушылар деп Гамильтон мен
Грассманды айтатындар баршылық. Бірақ аталмыш еңбектермен бір кезде дерлік
жарық көрген Сен-Венанның мемуарлары идея жағынан да, мазмұн жағынан да
Гамильтонның кватерниондар алгебрасына да, Грассманның геометриялық
анализіне де тәуелсіз, әрі өте құнды еңбек болып табылады.
Д. Валлис, Л. Карно, Сен-Венан, резаль бұлар векторлық алгебра мен
векторлық анализдің ұғымдарын ғылымға енгізді, механикаға қажетті
геометриялық аппарат жасау жолында жемісті еңбек етті.
Есептеудің жаңа түрі бойынша жинақталған бай, мазмұнды материалды
ортақ бір идея бойынша біріктіріп, механикалық “тұғырынан” ажыратып, бұл
апаратты математикалық пән дәрежесіне көтеру керек болды. Осыны Санкт-
Петербург университетінің профессоры Иосиф Иванович Сомов (1815-1876)
өзінің 1864-жылы жарық көрген “Об ускарениях различных порядков”, деп
аталатын еңбегінде абыроймен орындап шықты. Жоғарыда аттары аталған,
векторлық есептеулерді жасауға еңбек еткендердің негізгі көпшілігі
векторлық аппаратқа инженер көзімен қараса, И.И. Сомов математика көзімен
қарады.Ол векторлық есептеулерді математикалық пән жәрежесіне көтерді.
Сөйтіп, векторлық есептеулерге студенттер аудиториясына жол ашты: веторлық
есептеулерді механика оқулығына енгізді, ең алғашқы болып, дифферинциал
геометрияны векторларды қолданып, жазып шықты. Ол векторлық есптеулердің
бірқатар ұғымдары мен теоремаларын жасады. Векторлық аппаратты
пайдаланғанда нәтиже координаталар жүйесіне тәуелсіз екендігін ол бірінші
болып айтқан адам. Айналмалы қозғалысыт сол сияқты қисықтың бұралуын
зерттеу жұмыстарына векторлық көбейтіндіні қолдағанда да И.И. Сомов болды.
1918 жылы танымал математик Герман Вейль (1885-1955) векторлық
аксиоматиканы берді. Вейль аксиоматикасы қазіргі заман геометриясында, оның
қолдануларында пайдалануға аса қолайлы болып отыр.
Векторлық есептеулерді жасауға үлес қосқандардың ең көрнекті
дегендеріне қысқаша тоқталдық. Ғылымның бұл саласын дамытуға, практикада
қолдануға бұлардан басқа да үлес қосқандар аз болған жоқ. Солардың
қатарында: К.Бессель (1745-1818), К. Гаусс (1777-1855), Г. Белловитис (1803-
1880), К. Максвелл (1813-1879), Д. Гиббс (1839-1903), Л. Лоуренс (1901-
1958), А. Мебиус (1790-1858), Арган (1768-1882), Хивисоид т.б. атауға
болады.
Векторлық есептеулерді және олардың тамаша қолдануларын дамытуға И.
И. Сомовтан басқа да орыс және Кеңес ғалымдарының қосқан үлкен үлесі болды.
Осы тұрғыда атақты математик – Санкт-Петербург академиясының академигі М.В.
Остроградскийді (1801-1916) және П.А. Котельников, А.Л. Фридман, Н.Е.
Кочин, Я.И. Френкель (1894-1952), П.А. Широков (1895-1944), Д.И. Зейлиегер
(1864-1936) сияқтыларды атаған жөн.

1.2 Векторларға амалдар қолдану

Ғылым мен техникада кездесетін кейбір шамалар тек сан мәнімен ғана
сипатталады (абсолют шамасымен). Мысалы, масса, уақыт, температура және
т.б. Бұл шамаларды скаляр шамалар деп атайды. Ал, кейбір шамалар сан
мәнімен ғана емес, сонымен қатар бағытымен де сипатталады. Мысалы:
жылдамдық, үдеу, күш, импульс жәке т. б. Бұл - векторлық шамалар.
Бір қызығы, жоғарыда аталған барлық векторлық шамалар механикада
кездеседі. Алайда механиканың дамуы кезінде векторлық анализ тіпті
болмаған. Векторлық анализ тек Максвелдің электромагниттік теориясынан
кейін ғана пайда болды. Себебі, электр және магнит өрістерінің табиғаты —
векторлық.[5,7]
Кез-келген вектордын ұзындығы (вектордың шамасына пропорционал) мен
бағыты болады.
Векторларды қосу ережелері:
1) Үшбұрыш ережесі
2) Параллелограмм ережесі:
Векторлар — координаталар жүйелеріне тәуелсіз геометриялық объектер.
Мысалы А-векторы (1-сурет). Координаталар жүйесінің басынан басталып.

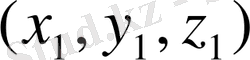
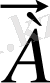
1-сурет
нүктесінде аяқталады. – импульс, күш, жылдамдық
болуы мүмкін. Ал координаталар жүйесінің басынан
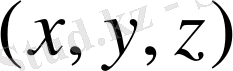нүктесіне дейінгі арақашықтықты арнайы -(радиус-вектор)
символымен белгілейді:
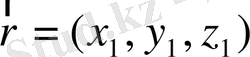(1.1)
-радиус-вектордың абсолют шамасы болсын. Демек,
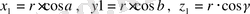(1.2)
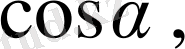
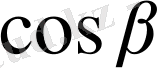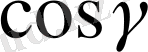Мұндағы және - бағыттаушы косинустар деп аталады, ал
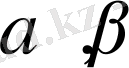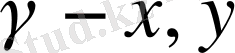және және 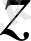осьтерінің оң бағыты мен - векторының
араларындағы бұрыш 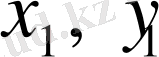және шамаларын - радиус
векторының (декарттық) компоненттері немесе проекциялары деп атайды.
Кез -келген векторын компоненттерге жіктеуге болады:
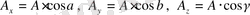(1.3)
Енді және 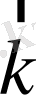- бірлік векторларын енгізейік. Олардың
ұзындықтары бірге тең және бағыттары 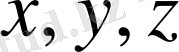остерімен бағыттас болсын. Онда,
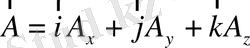(1,4)
Егер = 0 болса. онда Пифагор 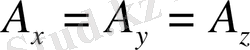теоремасы бойынша
векотырының абсолют шамасы:

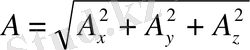
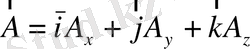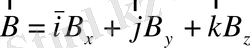Бізге және векторы берілсін, онда
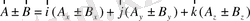(1.5)
Координаталар жүйесінің бұрылуы. радиус-векторды пайдаланып,
вектордың жңна анықтамасын берейік. Оған физикалық себептер бар. Біз
математика көмегімен табиғатты сипаттаймыз, сондықтан физикалық
сипаттауымыз математикалық аппаратқа тәуелсіз болуы керек. Егер физикалық
теорияны үй деп қарастырсақ, онда математика құрылыс саймандары.
Саймандарсыз құрылыс жүргізе алмаймыз. Құрылыс бітіргенде саймандарды
жинастырып қоямыз.
Кеңістікті изотропты деп қарастырайык. Демек, зерттелетін физикалық
жүйеміз немесе физикалық заң координаталар жүйесінің бағыттарына тәуелсіз.

2-сурет
радиус-векторын екі жүйеде қарастырайық, х және у осьтерін
сағат тілінің бағытына қарама қарсы бағытта бұрышына бұралық (2-
сурет). Пайда болған осьтерді х' және у' деп белгілейік. Сонда,
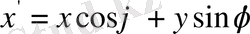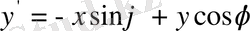, (1.6)
Егер 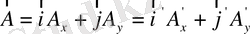, онда,
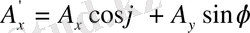б 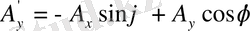(1.7) - координаталар жүйесін бұрған кездегі
векторлық компоненттерінің түрлену заңы. Егер 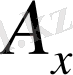және 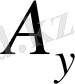екі
өлшемді радиус-вектор компоненттері сияқты түрлендірілетін болса, онда
олар векторының компоненттері болады. Егер 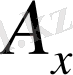және басқаша
түрлендірілсе, онда бұлардан вектор кұруға болмайды. Түсінікті болу үшін
(1.7) тендеуіндегі 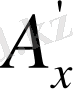және шамаларының мағынасын ізделік. А
векторы координаттар және кез келген векторының компоненттерінің
функциясы болсын:
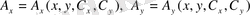(1.8)
Бұрылған кездегісі:
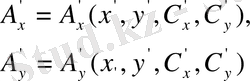(1.9)
(1.6) теңдеуін пайдаланып, 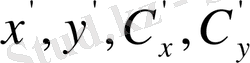координаттарын бұрылмаған
координаталар жүйесі мен бұрышы арқылы сипаттауға болады. Алайда
бұрышқа тәуелділік түсінік кеңістіктің изотроптылығына кайшы келеді.
Сондықтан бағытка тәуелсіз функциялармен шектелейік. Егер болса,
онда .
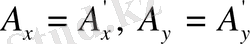Мысалы:
1. Екі шама берілген (-у, х). Екі өлшемді вектор құруға болатынын
көрсетіңдер.
Жүйені бүрышына бұрғанда осы шамалардың түрленуін қарастырайық.
,
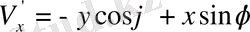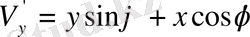
мұндағы 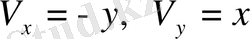(1.6) тендеуін пайдаланып., және 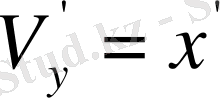екенін
көреміз.
Яғни, (1.7) тендеуін қанағаттандырады. Демек. (-у,х) жұбы вектор
компоненттері.
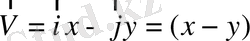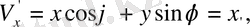
2. қарастырайық (1.7) теңдеуіне байланысты 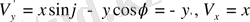және
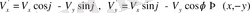, вектор бола алмайды. Осы теңдіктерді басқа түрде жазайық:
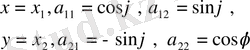(1.10)
(1.9) тендеуі:
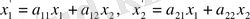(1.11)
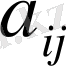коэффициенттерін бағыттаушы косинустар деп қарастыруға
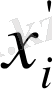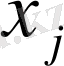болады. ( және , араларындағы бұрыш);

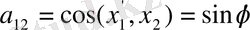
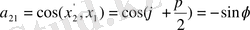
(1.11) теңдеуін қысқаша былай жазуға болады:
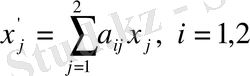(1.12)
Енді осы айтылғандарды 3,4 және одан көп өлшемдер үшін оңай жазуға
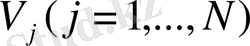болады. -өлшемі векторының компоненттерімен анықталады,
егер осы шамалар басқа (бұрылған) жүйеде мына теңдеумен берілсе:
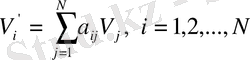(1.13)
мұндағы және араларындағы бұрыш.
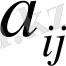коэффициентінің анықтамасынан декарттық координаттарда былай
жазуға болады:
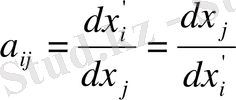(1.14)
Бұл дербес туындылар (1.14) теңдеуін (1.13) теңдеуіне қоялық:
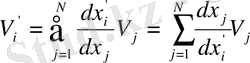(1.15)
Бағыттаушы косинустар 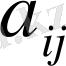ортогональдық шарттарын қанағаттандырады.

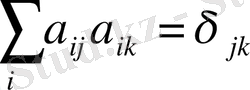(1.16)
немесе
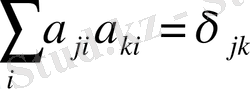(1.17)
Мүндағы - Кронекер символы,
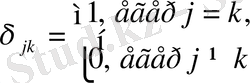(1.18)
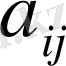мәндерін (1.10) тендеуінен (1.16) және (1.17)
тендеулеріне қойсақ, онда белгілі тендеуді аламыз:

(1.16) теңдеуінің дұрыстығына көз жеткізу үшін (1.14) өрнегін
пайдаланалық:
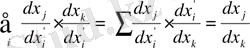(1.19)
Сонымен, вектордың компоненттерін түрлендіру заңдарының жаңа
анықтамасынан 2 жағдай шығады:
Әртүрлі физикалық кұбылыстарды сипаттауға қолайлы;
Математиканың жаңа бөлімі-тензорлық талдауға көшуге мүмкіндік береді.
Осыған байланысты жаттығулар көрсетілген (Қосымша А)
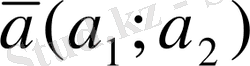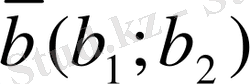Векторлардың скаляр көбейтінді. мен векторларының
скаляр көбейтіндісі деп санын атайды.
Анықтама. Нөлдік емес екі вектордың скалярлык көбейтіндісі деп
олардың ұзындықтары мен арасындағы бұрыштың косинусының көбейтіндісіне тең
сады айтыз.
=**Cos
1 болғандықтан
=* (21)
Егер векторлар координаталарымен берілсе =, =,
онда * және =, =.
Сонымен, * (22)
Үш өлшсмді кеңістіктсгі векторлар үшін
+ * (23)
Векторлардың скаляр көбейтіндісін де, сандарды көбейткендегідей,
жазып орындайды, скаляр кебейтінді деп атайды.[11,20]
Векторлардың математикалық көбейту зандары бір-біріне қайшы келмеуі
керек. Барлық мүмкін болатын анықтамалар ішінен физикаға және математикаға
қатысты қажетті екі анықтаманы тандалық. Үшінші тарауда басқа анықтама
беріледі.
көбейтіндісі физикада жиі кездеседі.
Мүндағы, А,В - екі вектордың абсолют шамалары, Ө - олардың арасындағы
бұрыш.
Мысалы: жұмыс =күш х жол х соsӨ.
Скаляр көбейтіндіні анықтайық ( және - векторы
үшін):
(1.20)
(1.20)
Бірлік векторлар үшін:
(1.20а)
(1.20в)
Егер осьтерді қайта бағыттап, х осін векторы бойынша
бағыттасақ, онда және (1.20)

(1.21)
Егер және болса, онда (1.20) және т.с. Басқаша
айтқанда, және — ортогонал векторлар. және
векторлары да өзара ортогонал.
Ортогоналдық түсінігін жалғастыралық, - бірлік векторы болсын,
ал -нөлдік емес, ху жазықтығында жататын вектор. Егер болса,
онда мұндағы - кез-келген вектор, онда векторы ху жазықтығына
перпендикуляр.
Енді скаляр көбейтіндінің скаляр шама екенін дәлелдейік. Ол үшін
көбейтіңдісін координаталар жүйесін бұру арқылы зерттейік. (1.13)
теңдеуінің арқасында:
(1.22)
және индекстерін пайдаланып, қысқаша жазалық: векторының
өз-өзіне көбейтіндісін қарастырайық:
(1.23), (1.24)
Сонымен (1.25)
Скаляр шама, координаталар жүйесін бұруға инвариантты.
векторының өз-өзіне көбейтіндісін қарастырайық:
(1.26)
(1.27)
(1.28)
А • В -координаталар жүйесін бұруға инвариантты, себебі (1.28)
теңдеуінің оң жағы скаляр шама. (1.26) тендеуін қайта. басқа түрде
жазалық:
(1.29)

8-сурет
Косинустар заңы. (1.26) және (1.29) теңдеуін салыстырып, косинустар
заңының векторлық табиғатын байқаймыз (3-сурет).
Векторлардың векторлық көбейтіндісі. Бұл көбейтіндіде екі вектордың
арасындағы бұрыштың синусын пайдаланады.
(1.30)
мұндағы, , бірақ мұндағы -вектор, және ол және
векторлар жатқан жазықтыққа перпендикуляр. , және
оң координаттар жүйесін құрасын, онда (коммут. емес).
(1.30а)
(1.306)
(1.30в)
Векторлық көбейтіндінің маңызды геометриялық қасиеті бар (4 сурет).

4-сурет
- параллелограмм ауданы.
Сонымен, векторы параллелограмм жазықтығына перпендикуляр, ал
абсолют шамасы осы параллелограмның ауданына тең болады екен.
векторлық көбейтіндінің басқа анықтамасы. -векторының
компоненттері:
(1.31)
және - әртүрлі. — (1.32) индекстерін циклді
өзгерту қажет.
Векторлық көбейтіндіні анықтауыш ретінде жазған ыңғайлы:
(1.33)

(1.30) және (1.31) көбейтіңділердің эквиваленттілігін көрсетейік.
Ол үшін және көбейтінділерін қарастырайық.
(1.34)
(1.35)
=(1.34) және (1.35) теңдеулерінен С векторы А векторына да, В
векторына да перпендиқуляр. А және В векторлары тиісті жазықтыққа
перпендикуляр.
(1.36)
(1.37)
(1.36) теңдеуінде көбейтіндісін (1.31) теңдеуі бойынша
компоненттерге жіктедік, содан кейін (1.20) скаляр көбейтіндісін
пайдаландық. (1.34), (1.35) және (1.37) теңдеулерінен (1.30) және (1.31)
анықтамалары эквивалентті екендігі шығады.
Енді вектор екенін керсетейік (яғни, вектордың түрлендіру
заңына бағынатынын). Бұрылған координаталар жүйесінде:
(1.38)
мұндағы. — циклдік ретте алуға тиіспіз. болғанда
(1.38) теңдеуі нөлге тең.
болсын, онда (циклдік рет):
(1.39)
(1.39) теңдеуін (1.38) теңдеуіне қоялық:
(1.40)
Осылай және үшін табамыз. Олар (1.13) шартын
қанағаттандырады. Яғни, -векторлык шама болып табылады.
Осыған байланысты жеке жаттығу жұмыстары көрсетілген. (Қосымша А)
Үш вектордың аралас және 2-реттік векторлық көбейтінділері
және - мұндай көбейтінділер комбинациясы жиі
кездеседі. Біріншісін аралас көбейтінді деп атайды.
- көбейтіндісінен шығатын векторлар А векторына
көбейтіледі, демек скаляр шама шығады.
- скаляр вектор, ал бүл операция белгісіз. Сондықтан
оны әзірге қарастырмаймыз.
(1.41)
(1.42)
(1.40) теңдігі жоғарғы ретті симметриялы (1.42) тендігінен шығады.
Үш вектордың аралас көбейтіндісінің геометриялық түсініктемесі бар.
Ол:егер, А,В және С векторлары параллелепипедтің "қабырғалары" болса онда
- көбейтіндісінің шамасы осы параллелепипедтің көлеміне тең болады
(әрине, аралас көбейтінді теріс санға да тең болуы мүмкін).
-2 рет векторлық кебейтіндіні қарастырайық. Бұл жолы жақшаны
сақтау керек (1.43)
Демек, бұл көбейтіндіден вектор шығады. Оның бағыты А және
(ВхС) векторлары жататын жазықтыққа перпендикуляр. - векторлары В
және С векторлары тиісті жазықтықта жатады. Себебі, ВС жазықтығы
векторына перпендикуляр. Сондықтан, векторының компоненттері В және С
векторларының сызықты комбинациясына байланысты:
(1.44)
Аралас және 2-реттік векторлық көбейтінділер арқылы одан көп
векторлар көбейтінділерін қысқартуға болады. Мысалы: Аралас көбейтінді
кері кристалл торларын есептеуде пайдаланады. және
(міндетті түрде өзара перпендикуляр емес)- кристалл торларын анықтайтын
векторлар болсын. Онда кез-келген 2 вектордың арақашықтығы
тендеуімен беріледі. Мұндағы, және пс - бүтін сандар.
(1.45)
векторларын жазуға болады. (1.50) = векторы ( және )
жазықтығына перпендикуляр, ал абсолют шамасы - ге пропорционал.
Шынында.
Соңғы тендеулер кері торларды анықтайды. Кері тор толқындардың
кристалдағы әртүрлі жазықтықтарда шашырауын есептеуге қажет. Векторлардың
аралас көбейтіндісіне шығаруға арналған есептер көрсетілген (Қосымша Ә).

1.3 Векторларды жіктеу тәсілдері

1) Векторларды координаттық осьтер бойынша жіктеу.
Егер вектордың абсолют шамасы бірге тең болса, оны бірлік вектор деп
атайды. Бағыты координаттың оң жарты осьтердің бағытындай бірлік векторлар
координаттық векторлар немесе орттар деп аталады. Біз оларды х осі бойында
және у осі бойында деп белгілейміз.
Ал координаттың векторлар нөлдік вектордан өзге және де коллинеар
емес болатындықтан, кез келген векторды осы векторлар бойынша
жіктеуге болады:
(*)
Осы жіктеудің мен коэффициенттерің табамыз. Ол үшін (*)
теңдіктің екі жақ бөлігін де векторына көбейтеміз. Сонда
, ендеше
(*) теңдіктің екі жақ бөлігін де е 2 векторына осылайша кебейтіп,
екенін табамыз.
Сонымен, кез келген векторды былай жіктеуге болады:

Сондықтан, егер болса, онда В нүктесі ОА жарты түзуінде жатады,
ал одан болса, мен векторлары бірдей бағытталады. Егер де
болса, онда В нүктесі толықтауыш жарты түзуде жатады да, мен
векторлары қарама-қарсы бағытталады. векторыньщ абсолют шамасы
мынаған тең:
Теорема дәлелденді.
Есеп. мен нүктелері берілген. Сонда АВ мен ВА
векторларының қарама-қарсы бағытталғанын дәлелдеңдер.
Шешуі. АВ векторының коордннаттары мен болады. ВА
векторының координаттары мен болады. Біз мынаны көріп отырмыз:
. Олай болса, АВ мен ВА векторлары қарама-қарсы бағытталған болып
шығады. .[8,7]
2) Векторды коллинеар емес екі вектор бойынша жіктеу.
Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес
екі вектор коллинеар векторлар деп аталадығ Коллинеар векторлар не бірдей
багытталган болады, не қарама-қарсы бағытталған болады.
Айталық, мен — нолден өзге коллинеар
векторлар болсын. Сонда саны табылып,
теңдігі орындалатынын дәлелдейік.
Айталық, мен векторлары бірдей багытталған болсын.
Сонда және векторлары да бірдей бағытталған және
олардың абсолют шамасы да бірдей болады. Демек. олар тең:

мен векторлары қарама-қарсы бағытталған
болғанда былай тұжырымдаймыз:
дәлелдемекшіміз де осы болатын.
Айталық, мен — нөлден өзге коллинеар емес векторлар
болсын. Енді кез келген векторды
түрінде көрсетуге болатынын дәлелдейік.
Айталық, А мен В - векторының басы мен ұшы болсын. А мен В
нүктелері арқылы және векторларына параллель түзулер
жүргіземіз. Олар қандай да бір С нүктесінде қиылысады. Сонда:
- мен векторлары коллинеар болғандықтан,
болады. мен векторлары коллинеар болгандықтан, болады.
Сонымен, дәлелдемекшіміз де осы болатын.

2 ВЕКТОРЛАРДЫ ЕСЕПТЕР ШЫҒАРУДА ҚОЛДАНУ

2.1 Алгебраның кейбір есептерін шығаруда векторды қолдану

Скалярлық көбейтінді көмегімен алгебралық есептерді шығару.
Векторлардың скалярлық көбейтіндісі геомстрия есептерін шығаруда,
тұжырымдарды дәлелдеуде көптеп қолданылады. Сонымен, қатар нөлдік емес екі
вектордың скалярлық көбейтіндісін теңсіздіктерді дәлелдеу, теңдеулерді,
теңдеулер жүйесін шешу және функцияның ең үлкен ең кіші мәндерін табу
есептерін шығарғанда пайдалануға болады.
1-есеп. -= х теңдеуін шешу керек.
Шешуі. Бірінші түбір астындағы өрнекті түрлендірейік:

Сонда =+6 (4)
Тендеудің мүмкін мәндер облысы [0; +], себебі х0 болу
керек.
=(х;3), ) векторларын енгіземіз, олардың
ұзындықтарын,скалярлык көбейтіндісін табамыз.
= ; = ; * х +6 (4)
теңдеуді
=* түрінде жазуға болады.
Соңғы теңдеу және векторларының арасындағы
бұрышының косинусы 1-ге тең болғанда яғни болса ғана орындалады.
Олай болса, .Олардың координаталары пропорционал х=0 мәні
теңдеуді қанағаттандырады, демек 0 - теңдеу түбірі.
х болғанда =; ; х=
Жауабы: )
2-есеп. 5 =4х+6у-3 теңдеуін шешу керек.
Шешуі. = (х:2у), =(4;3) векторларын қарастырамыз. Сонда
= ; ==5; =4х+6у.
(1) теңсіздікті қолдаисақ
54х+6у
Олай бслса, берілген теңдеудің шешімі жоқ.
3-есеп. Кез-келгсн х, у, z үшін х+у+z = 1 болғанда,
хуz екенін
дәлелдеу керек.
Дәлелдеуі.= , =векторларын еңгіземіз
* ++=(хуz ) =
= ; =
(3) теңсіздік көмегімеy хуz екенін аламыз.
4-есеп. Теңдеулер жүйесін шещу керек.
{++=1
++=4
Шешуі. ; векторларын алайық
= 1; ==
* =4
Берілгеи жүйені төмендегідей етіп жазамыз:

=4
болу керек, бізде 4 . Бұлай болуы мүмкін емес. Демек
теңдеулер жүйесінің шешімдері жоқ.
5-есеп. у=+функциясының ең үлкен мәнін табу керек.
Шешуі. Функция [-4,5; 6.5] кесіндісіінде анықталған.
= ; векторларын қарастырамыз, сонда
; * = + .
Демек, =(1) қасиетке сүйенсек, онда
Бұдан max = 2 . Бұл мәнді = болғанда қабылдайды.
Сонда, х=1 және у(-4,5)=, у(6,5)=
Жауабы:
6-есеп. у=4х+4x функциясы ең үлкен мән қабылдайтын х-тің
мәнін табу керек.
Шешуі. Функция барлық нақты сандар жиынында анықталған.
= 4х; 4x; =(1;1) векторларын еңгіземіз.
=2; =; *=4х+4x.
(1) 4х; 4x
Берілген функция екі өспелі функцияның қосындысы, демек ол да өспелі
болады. Ол максимумын 4х=4x болғанда кабьлдайды.
Бұдан =1, х=, nZ.
Жауабы: х=, nZ.
7-есеп.
теңсіздігі,
онын мағынасы бар барлық х үшін, орындалатындығын дәлелдеу керек.
Дәлелдеуі. Теңсіздіктің сол жағы анықталатын сандық аралықты табайық:
х-
х-1 х
х
=(1;1;2); және =() векторларын қарастырайық.
* =
= = =
(3) теңсіздіктен екені шығады.
8-есеп.
аболғанда а+в+стеңсіздігі орынды екендігін дәлелдеу
керек.
Дәлелдеуі. =() деп алсақ, (3) теңсіздікті пайдаланғанда
теңсіздіктің дұрыс екендігін көреміз.
Кесінділердің ұзындықтарын салыстырумен байланысты болып келген
геометриялық теңсіздіктерді және үшбұрыштың бұрыштарының тригонометриялық
функцияларымен байланысты болып келген теңсіздіктерді векторлық алгебраның
элементтерін пайдаланып дәлелдеуге болады.
Аталған теңсізліктерді векторлық әдісті пайдаланып дәлелдеуге жоғары
сынып окушыларын баулу — олардың математика пәніне деген шзығушылығы мен
ынта-ыкыласын арттырудың, матеыатикаіык білімІн терендетудін, математикалык
ұғышар жөнін-дегі тусініктерін байытудың, сондай-ак математика-лык
мәдениетін калшітастырудың кура^іы болып та-былатындығын ұзақ жылғы
педагогикалык іс-тәжі-рибеміз көрсетіп отыр.
Біз бұл макалада. аталган такырып бойынша жо-ғары сыныптардың
окушыларымен уйірмеде, факуль-тативте, қосымша сабактарда. математикалык
олим-пиада,іарға дайындау сабактарында, сондай-ак коры-тынды — кайталау
сабактарынла карастырып келген падагогикалык және вдістемелік бағыттағьг
зертгеу жұмысымыздын мазмұнына кыскаша токталмакпыз.
Окушыларды жоғарыда сөз болған тенсіздіктерці векторлық әдісті
пайдаланып, дәледлеуге баулуды іс жузіне асыруда, оларға мектеп геометрия
курсынан жаксы таныс келесі тенсіздіктерлі пайдаландык:
1. Кез келген екі және вектйрларының косындысынын
узындығы осы векторлардың ұзындықтарының қосындысынан артық емес, яғни
+ ; (А)
2. Кез келген = векторының скаляр квадраты — теріс емес
шама, яғни
=0; (В)

2.Кез келген екі және векторларының скаляр
көбейтіндісінің абсолют шамасы осы векторлардың ұзындықтарының
көбейтіндісінен артпайды, яғни
* * (С)
Мақалада жиі ұшырасатын кейбір кажетті ұғымдар, қатыстар және
белгілеулерге тоқтала кетейік, олар мыналар:
1. Үшбұрыштың медианалары әрқашан бір нүктеде қиылысады.
Медианалардың қиылысу нүктесі әрқашан үшбұрыштың ішінде жатады. Бұл нүкте
үшбұрыштың ауырлық центрі немесе центроиды деп аталалы.
2. Үшбұрыштың биіктіктері әрқашан бір нүктеде қиылысады.
Биіктіктердің қиылысу нүктесі берілген үшбұрыштың түріне байланысты оның не
ішінде, не сыртында жатады. Бұл нүкте үшбұрыштың орто-центрі деп аталалы.
3. Тетраэдрдың төбесі мен оған қарсы жатқан жататын центроидын
қосатын кесіңді тетраэдрдын медианасы деп аталады.
4. векторының ұзындығы деп оған сәйкес келетін АВ
кесіндісінің ұзындығын айтады, яғни
ав=ав.
5. векторынык скаляр квадраты оның ұзындығының квадратына
тең болады, яғни
Жоғарыда атап көрсетілген түрдегі есептерлі шығаруға кіріспес бұрын,
оқушылармен алдын ала кейбір маңызды да қажетті векторлық теңдіктерді
қарастырып алған пайдалы. Біз мұңдай векторлық теңдіктерді тірек есептері
ретінде қарастырдык және оқушыларға жан-жақты түсіндіре отырып, дәлелдеп
көрсеттік.
Төменде тірек есептері ретінде пайдаланылған векторлық теңдіктердің
негізгілерін (осы мақалаға қатысы барларын) ғана келтіреміз, олар:
1. = , (1)
= , (2)
мұндағы Q нүктесі — АВС үшбұрышының ВС қабырғасының ортасы,
G ңүктесі — NАВС тетраэдрыньң АВС жағының центроиды.
II. * = , (3) мүндағы А, В және С кез келген
үш нүкте. Мүндағы А, В және С кез келге үш нүкте.
III. = + +, (4)
= , (5)
мұндағы О нүктесі — АВС үшбұрышына сырттай сызылған шеңбердің центрі,
Н нүктесі — үшбұрыштың ортоцентрі, М — нүктесі үшбұрыштың цетроиды. Енді
мысалдар қарастыралық.
Векторларды мектептегі алгебра курсында көптеген мәселелерін оқытуда
да пайдалануға болатындығын іс-тәжірибеміз көрсетіп отыр.
Векторлық әдісті ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.