Жазықтықтағы нүктелердің геометриялық орыны

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе

1. Жазықтықтағы нүктелердің геометриялық орыны

1. 1. Нүктелердің геометриялық орыны туралы түсінік1. 2. Қарапайым геометриялық орындарға шолу1. 3. Геометриялық орынды іздеу

Кеңістіктегі нүктелердің геометриялық орыны2. 1. Негізгі геометриялық орындар2. 2. Екінші ретті беттер нүктелердің геометриялық орыны ретінде2. 3. Цилиндрлік бет нүктелердің геометриялық орыны ретінде

2. 4. Геометриялық орын әдісі

3. Аполлония шеңбері

4. Геометриялық орындарды аналитикалық геометрия әдістерімен іздеуге мысалдар

5. Геометриялық орын әдісімен салу есептерін шығару

Практикада қолданылуы

Қорытынды

Қолданылған әдебиеттер тізімі

Қосымша

КІРІСПЕ

Геометриялық орын түсінігі айтарлықтай әдістемелік және білім беру мәніне ие. Оның жазықтықтағы бейнеленуінен кеңістікте кескінделуі дамуындағы орынын бағалау қиын.

Геометриялық орын әдістері қолданылатын есептерді шешуде кеңістікте алдымен жеңілірек, одан кейін қиындау геометриялық денелердің қатынастарын орнату ыңғайлы.

Нүктелердің геометриялық орыны - басқа әр түрлі денелердің қиылысуы, беттесуі немесе олардың тіпті ортақ нүктесі болмауы мүмкін.

Нүктелердің геометриялық орыны деп бірнеше қасиеттерге ие болатын нүктелердің жиынтығын айтамыз.

Жазықтықта тек нүктелердің геометриялық орыны деп қарастырсақ, ал кеңістікте сонымен қатар түзулердің (түзу және қисық) де геометриялық орынын қарастыруға болады.

Сондықтан кеңістікте геометриялық орын дегеніміз - орны бір немесе бірнеше нақты шарттарды қанағаттандыратын көптеген элементтердің жиыны. Бұл жерде «нүкте» сөзінің орынына тек нүкте емес, түзуден де тұратын кең мағыналы «элемент» сөзі қолданылып тұр.

Бұл жұмыста кеңістіктегі нүктелердің геометриялық орнына көбірек тоқталамыз, себебі кеңістіктегі геометриялық орындар -бұл жазықтықтағы геометриялық орындардың жалпы жағдайы болып саналады.

Курстық жұмыстың мақсаты: жазықтықта немесе кеңістікте болсын нүктелердің геометриялық орыны туралы түсіндіре отырып, барлық денелер нүктелердің немесе қандайда бір қисықтардың геометриялық орыны екеніне көз жеткізу, сызбада көрсетіп, дәлелдеу.

Зерттеу объектісі негізінен нүктелер және олардың әртүрлі ортадағы орыны.

1. ЖАЗЫҚТЫҚТАҒЫ НҮКТЕЛЕРДІҢ ГЕОМЕТРИЯЛЫҚ ОРЫНЫ.

1. 1. Нүктелердің геометриялық орыны туралы ұғым.

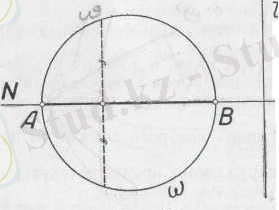Геометриялық денелер әртүрлі тәсілмен берілуі мүмкін. Денелердің қиылысуы немесе бірігуі түрінде, оның қасиеттерін анықтайтын нұсқау арқылы, оның әр нүктелерінің қасиеттері арқылы да тағы басқа түрде берілуі мүмкін.

Мысалы: Кез-келген АВ кесіндісін былай беруге болады(1-сурет) : 1) AM және BN сәулелерінің қиылысуы; 2) шеңберінің диаметрі; 3) l түзуіне параллель шеңберінің барлық хордаларының орталарының жиынтығы, және тағы басқа.

1-сурет.

Егер дене тек қана осы денеге тиісті нүктелердің қасиеттерімен берілген болса, онда бұл дене - нүктелердің геометриялық орыны деп аталады.

Бұдан берілген қасиеттерге ие болатын жазықтықтағы нүктелердің және тек қана осы нүктелерден құралған нүктелердің геометриялық орыны - дене деп аталады.

Біздің мысалда АВ кесіндісі l түзуіне параллель болатын шеңберінің хордаларының орталарының геометриялық орыны болып табылады. Осы немесе басқа да нүктелердің геометриялық орынымінезделетін қасиет осы нүктелердің геометриялық орынының характеристикалык қасиеті деп аталады.

Геометриялық денелер геометрияға жаңадан көбінде тек осы геометриялық орын ретінде енгізіледі.

Мысалға шеңбер - мектептегі геометрия курсында, эллипс, гипербала және парабала - аналитикалық геометрия курсында.

Аналитикалық геометрияда сызықтардың теңдеулерін құруда оларды нүктелердің геометриялық орыны ретінде қарастырады.

Нүктелердің геометриялық орыны тек қана сызық немесе бірнеше сызықтардың бірігуінен ғана емес, сонымен қатар нүктелердің ақырғы жиынтығы, жазықтықтардың ауданы және тағы басқа. Кейде тіпті бірнеше аталған қасиеттерге ие болатын нүктелердің геометриялық орыны мүлде болмайтын жағдай болады. Ф - дене аталған қасиеттерге ие болатын бұл нүктелердің геометриялық орыны екенін дәлелдеу үшін өзара кері мына екі сөйлемді дәлелдеу керек болады:

Ф- дененің әр нүктесі бұл қасиеттерге ие.
Аталған қасиеттерге ие болатын әр нүктеФденеге тиісті.

1. 2. Қарапайым геометриялық орындарға шолу.

Жазықтықтағы өте қарапайым нүктелердің геометриялық орыны мектепте геометрия курсында қарастырылады. Біз осылардың ең қажеттілерін қарастырайық.

1. О нүктесінен r қашықтықта жататын нүктелердің геометриялық орыны- бұл радиусы r , центрі О нүктесі болатын шеңбер болады.

2. Берілген екі нүктеден де бірдей қашықтықта жататын нүктелердің геометриялық орыны - бұл осы екі нүктені қосатын кесіндінің ортасынан өтетін және осы түзуге перпендикуляр болатын екінші бір түзуді береді. Бұл нүктелердің

2-cурет. геометриялық орыны кейде берілген нүктелердің симметриалі немесе медиатриссасы деп аталады(2-сурет) .

3. Берілген түзуден h қашықтықта орналасқан нүктелердің геометриялық орыны - берілген түзуге параллель түзулердің пары болып табылады. Бұл нүктелердің геометриялық орынын салу үшін а түзуінен кез- келген А нүктесін алып, сол нүктеден

3-сурет. болатындай р түзуін жүргіземіз. Енді а түзуінің екі жағынан да бірдей h қашықтықта а түзуіне параллель 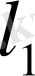және 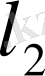түзуін жүргіземіз(3-сурет) .

4. Екі параллель түзуден бірдей арақашықтықтағы нүктелердің геометриялық орыны- бұл берілген екі түзуге параллель түзу болып табылады.

Бұл геометриялық орыны салу үшін а және в параллель түзулерін қиятын с түзуін

4-сурет. жүргіземіз. Осы кесіндінің ортасын тауып, сол нүктеден а және в түзулеріне параллель болатындай l түзуін жүргіземіз. Кейде бұл түзу берілген параллель екі түзудің ортаңғы түзуі деп те аталады(4-сурет) .

5. Қиылысатын екі түзуден бірдей қашықтықтағы нүктелердің геометриялық орыны - өзара перпендикуляр екі түзуді береді. Бұл түзулер берілген екі түзуден жасалған бұрыштардың биссектрисасы болып

5-cурет. табылады(5-сурет) .

1. 3. Геометриялық орынды іздеу.

Қандайда бір қасиетке ие болатын нүктелердің геометриялық орыны табыңыз - деге тапсырмалар практикада жиі кездеседі. Мұндай тапсырмалардың негізгі тоқтамы бірнеше «қарапайым» немесе «элементар» денелер жиынтығы белгіленіп алынғанын ұйғарады. Мұнда жиынтықтағы қай дене өзінен ізделінді геометриялық орынды көрсететінін табу керек. Бұл үшін алдын - ала белгілі, қарапайым, элементар болып есептелетін барлық денелердің тізімін құру қажет. Бұл тізім шартты болып табылады. Элементар планиметрия шарттарында белгілі болғандай элементар денелер қатарына мына денелерді жатқызамыз: барлық жазықтықтар, нүктелер, түзулер, кесінділер, сәулелер, шеңберлер, шеңбер доғалары. егер қандай да бір денелер екі элементар денелердің қиылысуы, бірігуі немесе айырымы болса, онда оларды да элементар денелердің қатарына жатқызамыз. Бұл тізім элементар денелер класын анықтайды. Бұл денелердің қатарына кез-келген нүктелердің жиынтығы, әртүрлі көпбұрыштар, дөңгелек, дөңгелекті сегмент, сектор, екі параллель түзудің арасындағы жолақ, жартылай жазықтықтар да кіреді. Берілген қасиеттерге ие болатын нүктелердің геометриялық орынын табу туралы тапсырманың нақты мағынасы ізделінді нүктелердің геометриялық орыны дәл қай элементар дене екенін көрсету үшін құрылған.

Нүктелердің геометриялық орынын табуға арналған тапсырмаларды шешу әдетте анализ жасауға, дәлелдеуге негізделеді. Бұл геометрияда салу есептеріне ұқсас. Бірақ нүктелердің геометриялық орынын табуды оны салумен алмастыруға болмайды. Кейде нүктелердің геометриялық орыны табылып және берілген құралдармен салыну мүмкін емес болады.

Анализ жасаудың мақсаты - ізделінді нүктелердің геометриялық орыны не болып табылатынына байланысты бірнеше гипотезалар жасау.

Анализ жасау әдетте чертежда берілген денені салады және болжам жасап қандай да бір ізделінді нүктелердің геометриялық орынына тиісті нүктені қарастырудан басталады. Бұл нүкте мен нүктелердің геометриялық орынының анықтамасынан шығатын және оның формасы мен жағдайын анықтауға көмектесетін берілген элементтермен бірнеше байланыстар жасайды. Кейде анализ жасауға қандай да бір жеке жағдайлар немесе ізделінді геометриялық орынға тиісті бірнеше нүктелердің өзіндік салынуы да себеп болады. Анализ қорытындысында есептің шешуіне біз тек қана болжалды жауап береміз. Оны ары қарай айқындап немесе дәлелдеу керек.

Дәлелдеу барысында екі өзара кері сөйлемдерді түсінеміз: 1) Анализ жасауда табылған дененің барлық нүктелері ізделінді нүктелердің геометриялық орынындағы нүктенің характеристикалық қасиеттеріне ие. 2) Характеристикалық қасиеттеріне ие барлық нүктелер анализ жасауда табылған денеге тиісті. (2) сөйлемді дәлелдеу келесі сөйлемді дәлелдеумен алмастырылуы мүмкін екенін де білу керек: ) Егер қандай да бір нүкте табылған денеге тиісті емес болса, онда ол нүкте характеристикалық қасиетке ие бола алмайды. Бұл сөйлемнің бірі анализ жасау барысында-ақ жиі қолданылатынын байқауға болады.

Зерттеу есепті шешу барысында мүмкін пайда болатын, осы немесе басқа да берілгендерді таңдауға байланысты әртүрлі жағдайларды қарастырумен қорытындыланады.

2. КЕҢІСТІКТЕГІ НҮКТЕЛЕРДІҢ ГЕОМЕТРИЯЛЫҚ ОРЫНЫ.

2. 1. Кеңістіктегі негізгі геометриялық орындар.

Қарапайым геометрия курсында және өмірде де кездесетін геометриялық орындарды көрсетейік. Геометриялық орындардың тізімі шексіз көп екеніне көз жеткіземіз.

Енді осы айтылған кеңістіктегі нүктелердің геометриялық орындарының біразын қарастырайық:

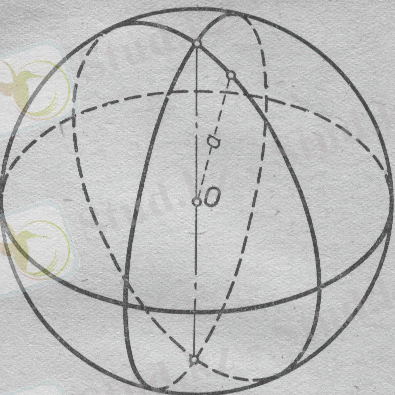
I. О нүктесінен бірдей а қашықтықта жатқан нүктелердің геометриялық орыны- центрі О нүктесі және радиусы а болатын сфера болады(1-сурет) .

II. в түзуінен бірдей а қащықтықта жатқан нүктелердің геометриялық орыны - цилиндрлік бет болады. в түзуі оның осі, ал

бағыттаушы шеңбердің радиусы - а , бұл жазықтық оське перпендикуляр болады.

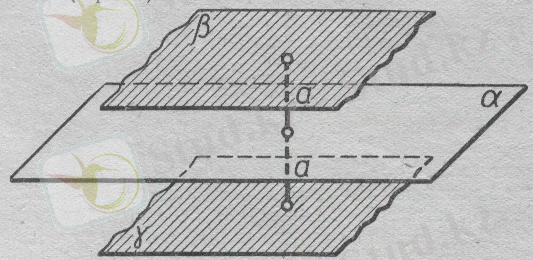
III. жазықтығынан бірдей қашықтықтағы (екі жағынан да) нүктелердің геометриялық орыны - жазықтығынан а қашықтықта жатқан екі параллель жазықтықтар болады(2-сурет) .

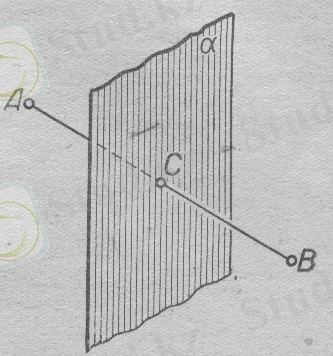IV. А және В нүктелерінен бірдей қашықтықта жатқан нүктелердің геометриялық орыны - АВ кесіндісінің ортасында орналасып және осы кесіндіге перпендикуляр болатын жазықтығы болады(3-сурет) .

V. Екі түзуден бірдей арақашықтықта жатқан нүктелердің геометриялық орыны.

Екі түзу кеңістікте параллель орналасуы, қиылысуы немесе айқасуы мүмкін екенін біз білеміз. Осыған байланысты нүктелердің геометриялық орыны әр жағдайда әртүрлі формаға ие болады.

а) а және в түзулері қиылысады. қиылысатын екі түзуден бірдей қашықтықта жатқан нүктелердің геометриялық орыны - екі өзара перпендикуляр болатын жазықтықтарын құрайды және а, в түзулерімен құралған бұрыштардың биссектрисаларынан өтеді.

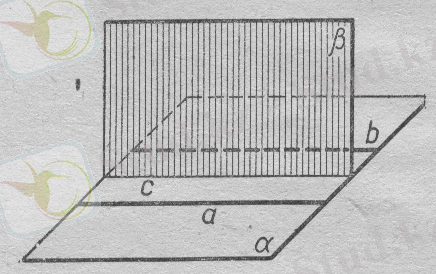
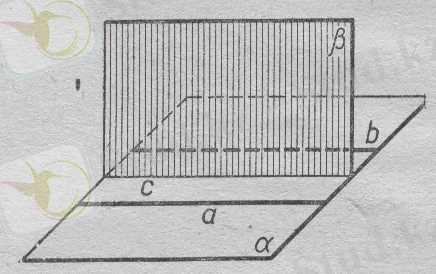б) а және в түзулері параллель. Мұнда түзулерден бірдей арақашықтықта нүктелердің геометриялық орыны - а, в түзулеріне параллель, с ортаңғы түзуінен өтетін және сол жазықтығына перпендикуляр болатын 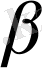жазықтығын

береді(4-сурет) .

в) а және в түзулері айқасады. Мұндай жағдайда нүктелердің геометриялық орыны бір немесе екі жазықтықтар болмайды, онда ол күрделі формаға ие болады.

Бұл геометриялық орындардың қасиеттерін анықтау үшін былай талқылаймыз: а және в түзулері айқасқан түзулерін с түзуімен қиамыз. Сонда а және с қиылысқан түзулерден бірдей арақашықтықта жатқан нүктелердің геометриялық орыны - 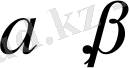екі жазықтығы болады. Ал, в және с түзулерінен бірдей арақашықтықта жатқан нүктелердің геометриялық орыны -басқа бір 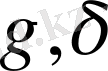екі жазықтығы болады. Біруақытта 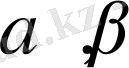жазықтығына және 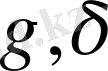жазықтығына да тиісті нүктелер а, в және с түзулерінен бірдей қашықтықта болады, сондықтан 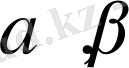жазықтығының 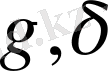жазықтығымен қиылысқандағы төрт түзу ізделінді нүктелердің геометриялық орынын береді.

Енді а және в айқас түзулерін қиятын 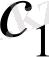түзуін жүргізейік. Жоғарыдағыдай талқылай отырып, біз тағы да ізделінді геометриялық орынға тиісті төрт түзуді аламыз.

Осылайша бірдей қашықтықта жататын шексіз көп түзулерді алуға болады. бұл түзулердің барлығы да бір бетте жатады. Бұл бетті осы түзулердің тұғыры деп қарастыруға болады, сондықтан а және в айқасқан түзулерінен бірдей қашықтықта жататын нүктелердің геометриялық орыны - қандайда бір түзу сызықты бет болады. бұл бет гипербалалық парабалоид деп аталады және ер тәрізді формада болады(5-сурет) . Бұл гипербалалық парабалоид екеніне бұл беттің аналитикалық теңдеуін декарттық координатаға салу арқылы көз жеткізуге болады. Біз барлық геометриялық орынды қарастырмай, тек қана бірнеше жай ғана алынған түзулерден құрылған бөлігін қараймыз және оларды шартты түрде а, в түзулерінен бірдей қашықтықта жатқан нүктелердің геометриялық орыны деп есептеймсіз.

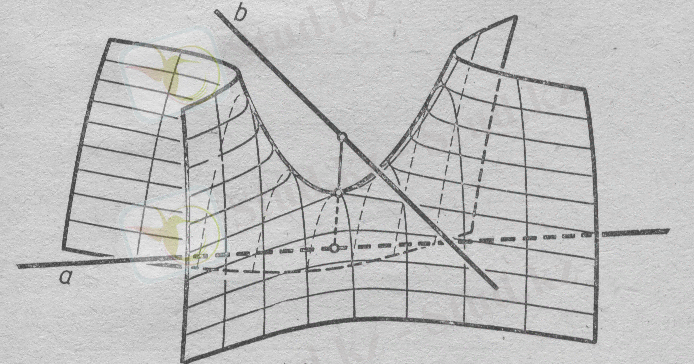
VI . α, β қиылысатын екі жазықтықтан бірдей қашықтықта жататын нүктелердің геометриялық орыны -осы жазықтықтармен жасалған екі жақты бұрыштарды қақ бөлетін екі өзара перпендикуляр γ және δ жазықтықтарын береді(6-сурет) .

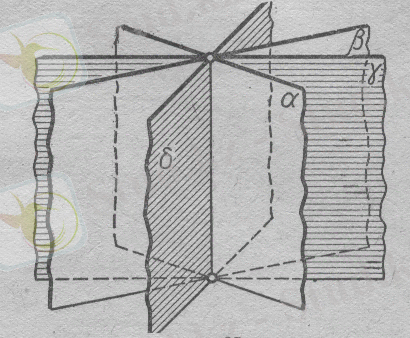
VII. Үш нүктеден бірдей қашықтықта жатқан нүктелердің геометриялық орыны . Мұнда 2 жағдай мүмкін:

а) Берілген А, В және С нүктелері бір түзудің бойында жатпайды. Бұл жағдайда ізделінді геометриялық орын - берілген үш нүктеден анықталған жазықтыққа перпендикуляр болатын АВС үшбұрышының әр қабырғасының ортасына жүргізілген перпендикуляр түзудің қиылысу нүктесі арқылы өтетін а түзуі болып табылады. Бұл түзу АВ, АС, ВС түзулерінің ортасы арқылы өтетін және оларға перпендикуляр орналасқан үш жазықтықтың қиылысу сызығы болады(7-сурет) .

б) Берілген А, В, С нүктелері бір түзудің бойында жатады. Бұл жағдайда геометриялық орын жоқ. Себебі кеңістікте қажетті шартты қанағаттандыратын ешқандай нүкте жоқ, АВ және ВС кесінділерінің ортасынан өтетін және перпендикуляр болатын жазықтықтар өзара параллель болады, яғни қиылыспайды.

VIII. Үш түзуден бірдей қашықтықта жатқан нүктелердің геометриялық орны. Мұнда төмендегі жағдайларды қарастырамыз:

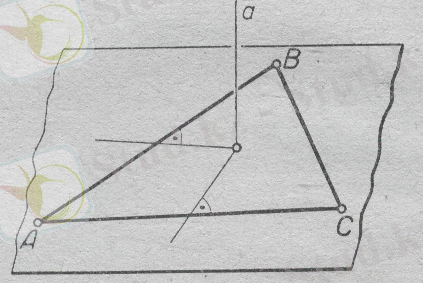
а) Үш түзу (бір α жазықтықта жататын) бір нүктеде қиылысады. Мұнда әр түзуден бірдей арақашықтықта жататын нүктелердің

8-сурет. геометриялық орны - қиылысу нүктесі арқылы өтетін және берілген α жазықтыққа перпендикуляр болатын түзуді береді(8-сурет) .

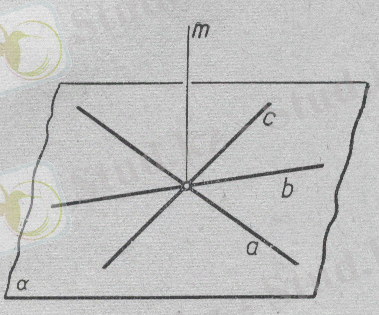
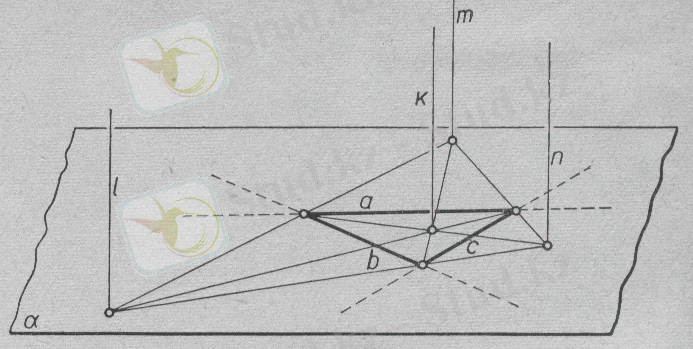
б) Үш түзу α жазықтықта қос-қостан қиылысады. Ізделінді геометриялық орын - осы α жазықтығына перпендикуляр болатын, ішкі

9-сурет. және сыртқы бұрыштардың биссектрисалары

қиылысатын

нүктеден өтетін төрт түзу болады( k, l, m, n ) (9-сурет) .

в) Екі түзу параллель және үшіншісі сол екі түзуді қиып өтеді. Екі паралель а, в және оларды қиып өтетін үшінші с түзуден бірдей қашықтықта жататын нүктелердің геометриялық орны - осы түзулер жататын α жазықтығына 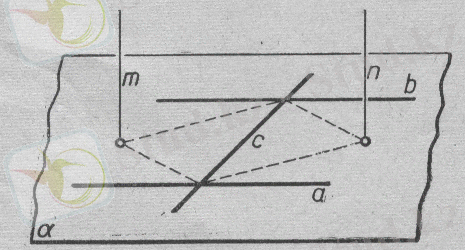перпендикуляр болады және осы түзуден құралған ішкі бұрыштардың бисектриссаларының қиылысу нүктесінен өтетін m және n түзулері болып табылады(10-сурет) .

г) Бір α жазықтықта жататын үш өзара параллель түзулер. Бұл жағдайда үш параллель түзулерден бірдей арақашықтықта жатқан, және бір

түзуде жататын ешқандай нүкте жоқ, яғни нүктелердің геометриялық орны болмайды(11-сурет) .

д) Үш түзу ( а, в, с ) Ѕ нүктеде қиылысады, бірақ әр түрлі жазықтықта жатады.

Мұндай жағдайда, әр түзуден бірдей қашықтықта жататын нүктелердің геометриялық орны - Ѕ қиылысу нүктесінен өтетін төрт түзу болады.

Бұл геометриялық орынды салу үшін а және в түзулерінен бірдей қашықтықта жататын нүктелердің геометриялық орнын қарсатырамыз. Бұл бізге белгілі екі α, β жазықтығы болатыны анық. Сол сияқты в және с түзулерінен бірдей арақашықтықта жататын нүктелердің геометриялық орны - γ, δ жазықтықтары болады, ал с және а тірдей қашықтықта жататын нүктелердің геометриялық орны - ε, ρ жазықтықтары болады. (V, а, г, о)

α және β жазықтықтары γ, σ және ε, ρ жазықтықтарымен ĸ, l, m және n түзулері арқылы қиылысады. Бұл түзулер берілген үш түзудің қиылысу нүктесінен өтеді. Сондықтан берілген үш түзуден бірдей қашықтықта жататын ізделінді нүктелердің геометриялық орны - осы төрт түзу болады.

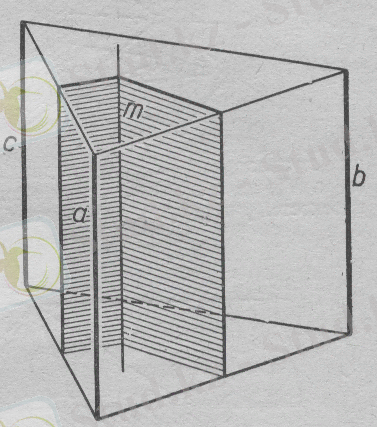е) а, в, с үш түзуі әр түрлі жазықтықта өзара параллель орналасқан. Мұндай жағдайда үш түзуден бірдей арақашықтықта орналасқан. Нүктелердің геометриялық орны - берілген түзуге парллель болатын және үш жазықтықтың қиылысу сызығы болатын m түзуі болып табылады.

Бұл үш жазықтықты алу үшін V, б - геометриялық орынды ең алдымен а және в -ға, одан кейін в және с -ға және а және с -ға қолданамыз(12-сурет) . Әрине m түзуін алу үшін үш жазықтықты бірдей салудың қажеті жоқ, олардың екеуін салса да жеткілікті.

IX. Үш жазықтықтан бірдей қашықтықта жатқан нүктелердің геометриялық орны.

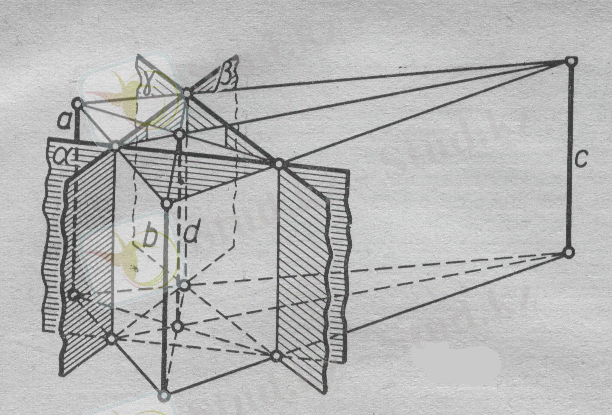а) α, β, γ жазықтықтары бір нүктеде қиылысады. Бір нүктеде қиылысатын жазықтықтардан бірдей арақашықтықта жататын нүктелердің геометриялық орны- бұл осы нүкте арқылы өтетін төрт түзудің негізі болып табылады.

б) α, β және γ жазықтықтары параллель түзулер арқылы қиылысады.

Параллель түзулер арқылы қиылысатын үш жазықтықтан бірдей қашықтықта

орналасқан нүктенің геометриялық орны - қиылысу түзулеріне параллель болатын төрт а, в, с және д түзулері құрайды(13-сурет) .

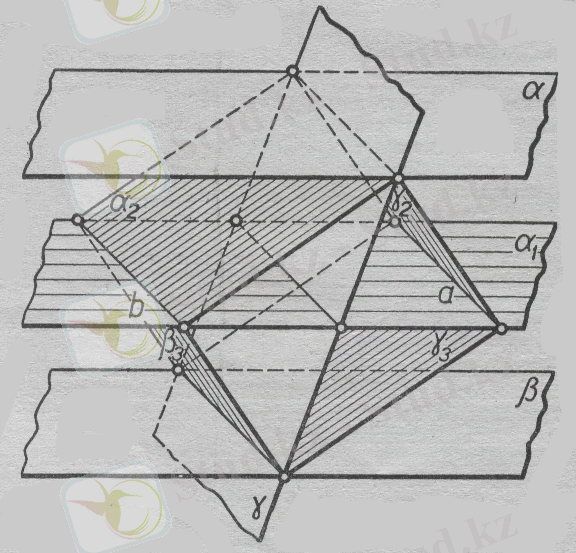
в) Екі α және β жазықтықтары параллель, ал үшінші γ жазықтықтығы оларды қиып өтеді.

Мұндай жағдайда ізделінді геметриялық орын - екі түзу. Расында да, α және β жазықтықтарына бірдей қашықтықта жатқан нүктелердің геометриялық орны - α ₁ жазықтығы

14-сурет. болсын (VI, б -г. о. ) (14-сурет) . α және γ жазықтықтарынан бірдей жазықтықта биссекторлық жатқан нүктелердің геометриялық орны - α ₂ жазықтықтары γ ₂ жазықтықтары болады (VI, а, г. о. ), ал, β және γ жазықтықтарынан бірдей қашықтықта жатқан нүктелердің геометриялық орны - β ₃ және γ ₃ екі биссекторлық жазықтықтары болады (VI, а, г. о. ) .

Енді α _1, γ ₂ және γ ₃ жазықтықтары а түзуі арқылы, ал α ₁ , α ₂ және β ₃ жазықтықтары в түзуі арқылы қиылысатынын және а, в түзулері берілген α, β, γ жазықтықтарына параллель болатынын оңай көрсетуге болады.

г) Үш жазықтық өзара параллель болады.

Мұндай жағдайда үш жазықтықтан біруақытта бірдей арақашықтықта ешқандай нүкте жоқ, яғни нүктенің геометриялық орны болмайды.

д) Үш жазықтық бір түзу арқылы қиылысады. Осындай үш жазықтықтан бірдей арақашықтықта жататын нүктелердің геометриялық орны - берілген жазықтықтықтардың қиылысу сызығы болатын а түзуімен беттеседі, сондықтан барлық нүктелердің геометриялық орнынан үш жазықтыққа дейінгі арақашықтық 0-ге тең.

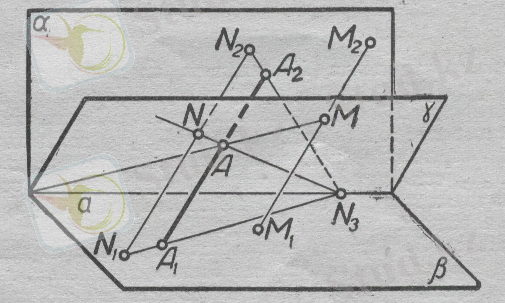
Х. Берілген екі жақты бұрышқа жүргізілген түзулердің параллель кесінділердің әрбіреуі берілген қатыныста бөлетін нүктелердің геометриялық орны - бұл бұрыштық қабырғасы арқылы және осындай бір нүктеден өтетін жазықтық болып табылады(15-сурет) .

α және β жазықтықтары а түзуі арқылы қиылысатын берілген екі жақты бұрышты құрасын. А ₁ , А ₂ түзуі - берілген бұрышқа жүргізілген параллель түзулердің кесіндісі және А нүктесі d нүктесі d ₁ d ₂ түзуін берілген қатынаста бөледі.

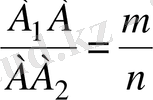_; m және n - берілген сан немесе кесінді. А нүктесі және а түзуі қандайда бір γ жазықтығын анықтайды.

Енді N ₁ N ₂ - кез келген А ₁ А ₂ -ге параллель кесінді болсын және N нүктесі мына қатынасты қанағаттандыратындай етіп алынған ;

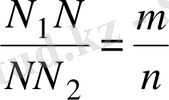Енді N нүктесі γ жазықтығында жататынын дәлелдеу керек.

А ₁ А ₂ және N ₁ N ₂ арқылы өтетін және а түзуін N ₃ нүктесі арқылы жазықтық жүргізейік. Сонда N ₃ А түзуі γ жазықтығында жататын болады.

Бұрыштық N ₁ N ₃ N ₂ -ның қабырғасын қиятын параллель кесінділерді берілген қатынаста бөлетін ( N ₁ А ₁ А ₂ N ₂ ) жазықтығы нүктелердің геометриялық орны- осы бұрыштың төбесінен және осындай нүкте арқылы өтетін түзу болғандықтан, N нүктесі АN ₃ түзуіне тиіс және сондықтан γ жазықтығында жатады.

Салдар:

Екі жақты бұрыштың әрбіреуі қабырғасына дейінгі арақашықтықта жатқан барлық нүктелер берілген қатынаста орналасады, екі жақты бұрыштың қабырғасынан өтетін және осындай бір нүкте арқылы өтетін жазықтықта жатады.

ХI. Берілген кесінді тікбұрышпен көрінетін нүктелердің геометриялық орны - сфера болады. Берілген кесінді осы сфераның диаметрі.

Бұл геометриялық орын жазықтықтағы белгілі геометриялық орының табиғи жалпыланған түрі: берілген түзу тікбұрышпен көрінетін нүктелердің геометриялық орны - берілген түзу диаметр болатын шеңбер.

Егер берілген түзу қандай да бір түзуге тиісті емес нүктеден ϕ бұрышы арқылы көрінсе, онда геометриялық орын күрделірек формаға ие болады. Берілген кесінді ϕ бұрышпен көрінетін нүктелердің геометриялық орыны берілген кесіндіге сырттай сызылған және осы кесіндінің айналасында ϕ бұрышы кірістірілген шеңбер доғасының айналуынан пайда болған бет болып табылады. Бұл бет тор деп аталады.

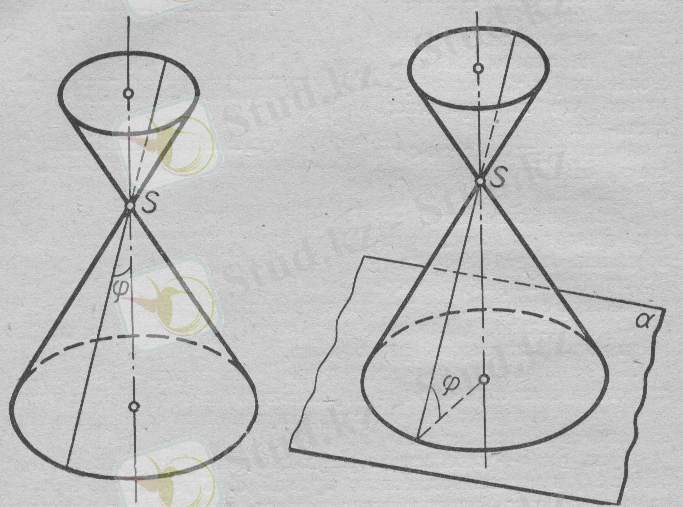ХІІ. а) Берілген түзудегі S нүктесінен өтетін және осы түзумен бірдей ϕ бұрыш жасайтын түзулердің геометриялық орыны - конустық бет болады (16-сурет) .