Турбуленттіктің статистикалық сипаттамалары және пульсациялардың стандарттары мен ықтималдылығы


Реферат
«Турбуленттіліктің негізгі статистикалық сипаттамалары. Турбуленттік пульсациялардың стандарттары мен ықтималдылығы. »
- Турбуленттіліктің негізгі статистикалық сипаттамалары
- Турбуленттік пульсациялардың стандарттары мен ықтималдылығы
1. Турбуленттіліктің негізгі статистикалық сипаттамалары
Турбуленттік ағыстың кездейсоқ сипаттамасы статистикалық түрде тиімдірек сипатталады.
Турбуленттіліктің негізгі статистикалық сипаттамаларының бірі ретінде құйынды құрылымды орташа масштабтар мен турбулентті пульсация жылдамдығының қарқындылығы жатады.
Құйынның сызықты масштабы анализден алынған корреляция функциясымен орындалуы мүмкін.
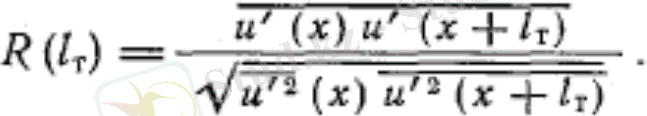 (1)
(1)
Корреляция функциясының мәні бір-бірінен l t қашықтықта орналасқан ағыстың екі нүктесіндегі пульсация жылдамдығының бірмәнді өзгергіштігі дәрежесін сипаттайды.
Корреляция функциясының мәні уақыт бойынша орташаландырылған жағдайда азаяды. Кейбір l t =L үлкен мәндерінде корреляция функциясының мәні нольге қарай жақындайды. Егер корреляция функциясының l t >L мәндерінде мағынасы теріс мәнді болуы мүмкін. Бұл жағдайды бақылау нүктелерінің орналасуы құйынның екі жағында алшақ болуымен түсіндіруге болады. Турбуленттіліктің макромасштабтылығы (немесе интегральды масштаб)
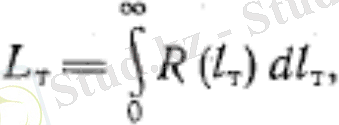 (2)
(2)
ағыста кездесетін ең үлкен құйындылардың орташа өлшемін көрсетеді.
Корреляция пульсацияның бір құрамы үшін, әртүрлі құрамы үшін, және де әртүрлі пульсация сипаттамалары үшін зерттеле береді. Жоғарыда қарастырылған корреляция кеңістіктік екі нүктелі болып саналады. Сонымен қатар, бірнүктелі корреляцияны да (немесе автокорреляцияны) R(t) зерттеуге болады.
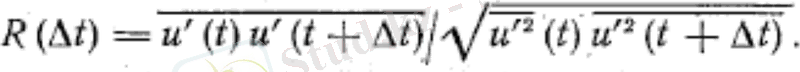 (3)
(3)
Автокорреляция кеңістіктік корреляция сияқты турбуленттіліктің уақытты макромасштабын анықтауға мүмкіндік береді:
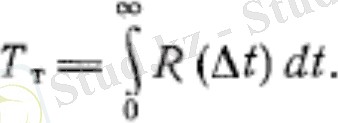 (4)
(4)
Құйындарды u жергілікті ағыс жылдамдығына тең мәнмен салыстырмалы түрде қозғалыссыз бақылау нүктесіндегі жылдамдықпен орын ауыстырады деп санап, уақытты және кеңістікті турбулентілік масштабтарының байланысын орнатуға болады.
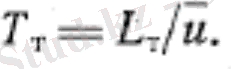 (5)
(5)
Бұл қатынас "мұздатылған турбуленттілік" гипотезасы атымен белгілі. Гипотеза турбуленттіліктің статистикалық теориясының негізін салған Дж. Тейлор арқылы алғышқы рет көрсетілген.
Әртүрлі масштабтағы құйындардың пульсациялық энергиясы да бір-бірінен өзгеше болып келеді. Турбуленттік пульсацияны құрамындағы гармоникаларына қарай бөлшектеп, турбуленттік энергияның шамасын е і және сәйкесінше әрбір гармониканы n i , яғни құйынды өлшеміне арналған.
Пульсацияның типтік жиілік-знергетикалық спектрі (1-сурет) арқылы үш сипаттамалы ауданға бөлуге болады.
1. Үлкен өлшемді құйындар ауданы. Энергияны орташаланған ағыстан алып, және оны кішірек масштабты құйындыларға жібереді. Үлкен құйындар барлық турбуленттіліктің кинетикалық энергиясының 20% -ын ұстайды.
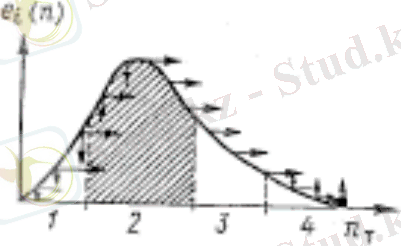 1-сурет. Жиілік-энергетикалық спектр.
1-сурет. Жиілік-энергетикалық спектр.
Горизонтальді нұсқаушалар энергияның бір жердегі спектрлік ауданынан екіншісіне берілуін көрсетеді. Ал вертикальді нұсқаушалар: төмен- турбуленттілік генерациясы, жоғары- энергияның жылуға диссипациясын; 1-үлкен құйындар, 2-энергияжібергіш құйындар, 3-инерциялы интервал, 4-диссипация интервалы.
2. Энергия сақтаушы құйындар ауданы, мұнда турбуленттілік энергиясы спектрінің максимум мағынасына жетеді.
3. Бұл ауданда турбуленттілік статистикалық баланста тұрып, ағыстың интегральдық сипаттамасына тәуелсіз кездесуі. Энергияжібергіш құйындар арқылы турбулентілік энергиясының ағыны келеді.
Өлшемдер және есептік тәуелділіктер анализі нәтижесінде спектральді тығыздық S(n t ) ұғымын жиі қолданады.
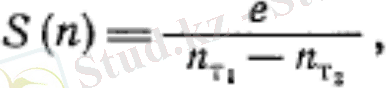 (6)
(6)
мұнда n t1 - n t2 -фильтрдан өтетін жиілік сызығы шекарасы.
Құйын жиілігінің ( яғни өлшемі азаюы) өсуі арқылы тұтқырлық рөлі же өседі. Максималды диссипация интервалында турбуленттілік екі шамамен анықталады: диссипация және тұтқырлық v. осы екі шама арқылы құйындар масштабын білеміз.
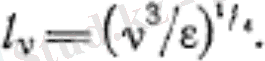 (7)
(7)
Спектральді тығыздық пен орнатылмаған корреляция функциясы кездейсоқ процесстердің бірдей ақпаратын сақтайды. Корреляция функциясы құйынды құрылымдардың масштабының анализі және өлшемдері үшін онайырақ болып келеді. Спектральді тығыздық турбуленттілік энергиясының пульсация жиілігі бойынша үлестірілімі үшін анық көрініс береді. Сондықтан спектральді тығыздық пен корреляция арасындағы байланысқа қызығушылық мол. Кездейсоқ теория функциясы дәлелдегендей, спектральдә функцияны орнатылмаған корреляцияның cos өзгергіштігінен алуға болады:
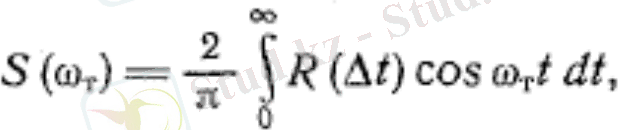 (8)
(8)
мұнда w t =2πn t -дөңгелек жиілік.
Турбулентік пульсацияның уақыт бойынша өзгеруі кездейсоқ сипатта болады. Сондықтан пульсацияның энергиялық және кеңістіктік қана емес және ықтималдылық сипаттамасын бақылау да қызық. Кездейсоқ процесстердің негізгі ықтималдылық сипаттамасы ретінде ықтималдылық үлестірім заңын санаймыз. Ол дифференциалды және интегралды өлшемде болуы мүмкін. Ықтималыдылықтың үлестірім заңы арқылы кездейсоқ процесстер туралы толық мәлңмет алуға болады, бірақ заңның өзін ғана емес және де оның шамаларын есептеу тиімдірек. Осы шамалардың бірә ретінде үлестірім моменттерін атауға болады.
Үлестірім моменттері турбулентіліктің қарқындылығын, симметриялығын және де қарастырылып отырған статистикалық процесстің максималды пульсациясын сипатпайды.
Турбуленттілік пульсациясының ықтималдылығының ең жиі қолданылатын заңы ретінде нормальді үлестірім заңын немесе Гаусс заңын атауға болады. Ықтималдылық үлестірім тығыздығы бұл жағдайда келесі қатынас арқылы анықталады:
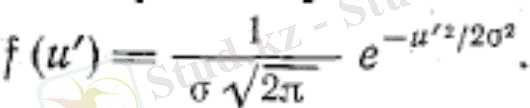 (9)
(9)
Турбуленттіліктің статистикалық сипаттамаларын зерттеу анық ориентациядағы өлшегіш құралдардың векторға орташаланған жылдамдығы мен беттік үйкелу өлшеулерінің нақтылығын қажет етеді. өзен түбінің кішігірім біркелкі еместігіне байланысты бұл өлшем бекітулері қиын. Сондықтан өзен турбуленттілігіне келтірілген лабораториялы зерттеу жұмыстары жүргізіледі.
2. Турбуленттік пульсациялардың стандарттары мен ықтималдылығы
Турбуленттіліктің өзен түбінің шайылуына, тасынды бөлшектерге әсері ең алдымен турбуленттілік қарқындылығына және оның ықтималдылығына байланысты. Турбуленттілік қарқындылығын пульсацияның орташа квадраттық мәні ретінде саналатын пульсация стандартымен сипаттаймыз. Алайда пульсация стандарты турбуленттіліктің ағыс түбәне әсерін толықтай көрсетпейді. Бұл жерде әртүрлі өлшемдегі пульсацияның пайда болу ықтималдылығы да рөл ойнайды. Пцльсация ықтималдылығы артқан сайын грунттағы бөлшектердің тасындыға айналу жиілігі ұлғаяды.
Турбуленттік пульсация ықтималдылығының үлестірім заңы u ' x және u ' z жылдамдықтары Р ықтималдылық мүмкін болатын жылдамдықтағы барлық пульсация құрамы мәнін сипаттайды.
Ықтималдылықтың үлестірім заңын тәжірибелер арқылы зерттеу нормал үлестірім заңына бағынатын кездейсоқ процесстерге турбуленттік пульсация жылдамдығының ұаншалықты жағындығын орнатуға мүмкіндік береді. 2-суретте вертикальді және бойлық бойынша пульсация жылдамдығының интегральді формасы берілген.
Пульсацияның пайда болу ықтималдылығы екі еселік стандарт бойынша 2, 5%-ға дейін азаяды. Ал улкен мәнді пульсацияның ықтималдығы 3 есеге артылу стандарты бойынша 0, 3% болады.
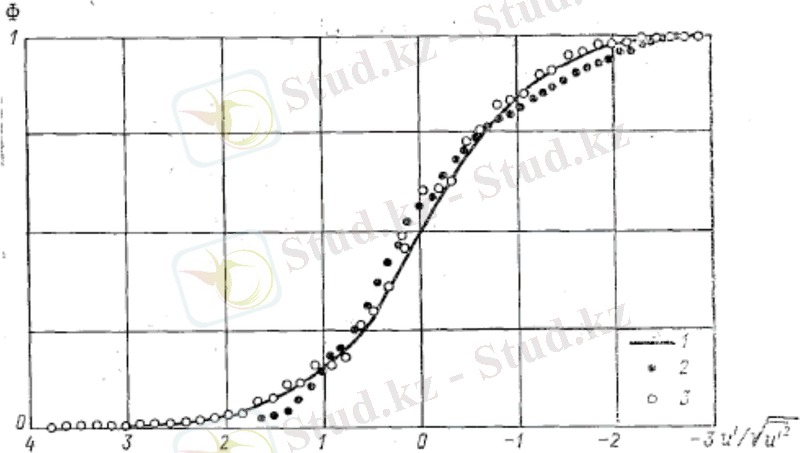
2-сурет. Пульсациялық жылдамдықтың интегральді үлестірім ықтималдылығы
1-нормальді үлестірім, 2-вертикальді пульсация, zh=0. 53. 3-бойлық пульсация, zh=0. 14.
Салыстыру тәжірибе арқылы алынған мәліметтердің ықтималдылығының нормальді үлестірім заңына сәйкестігін көрсетеді. Ықтималдылықтың үлестірім заңын зерттеу көп жағдайда оны анықтайтын сипаттамалары арқылы немесе орталық моменттері арқылы жүргізіледі. Бірінші орталық момент кез келген кездейсоқ шама үшін анықтамасы бойынша нольге тең. Ал екіншісі, кездейсоқ шаманың шашылу дәрежесін анықтайды да, кездейсоқ процесстің маңызды сипатаамасы болып табылады және осы жағдайда пульсациялық жылдамдықтың стандартын анықтайды.
Ашық ағыстың тереңдігі бойынша бойлық пульсация стандартының типтік үлестірілімі u ' x және вертикальді пульсациялық жылдамдықтың стандарты u ' z 3-суретте көрсетілген. Пульсация стандарты мұнда динамикалық жылдамдыққа қатысты алынған , мұндағы һ-ағыс тереңдігі.
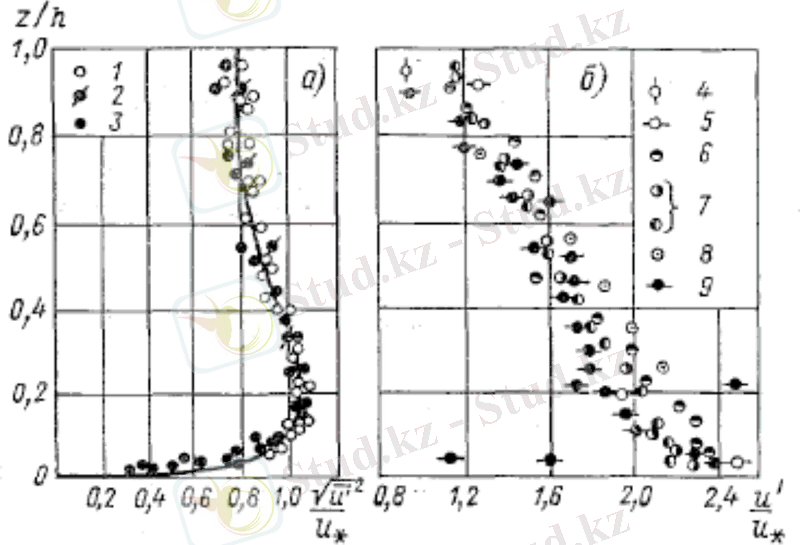
3-сурет. Ағыс тереңдігі бойынша пульсация жылдамдығының стандарттарының типтік үлестірілімі.
а-вертикальді пульсация, б-бойлық пульсация; 1-суландыру каналдарындағы өлшеу, 2-Минск тәжірибесі, 3-Никитин тәжірибесі, 4-Фидман тәжірибесі, 5-Дж. Лоренц тәжірибесі, 6-Ж. Лаври тәжірибесі, 7-К. Элата және А. Т. Иппен тәжірибесі, 8- Никитин тәжірибесі, 9-Минск тәжірибесі.
Осы үлестірімдер арқылы келесі сипаттамалық өзгешеліктерін анықтаймыз: канал түбіне жақын аймақта бойлық пульсация стандарты максималды болады.
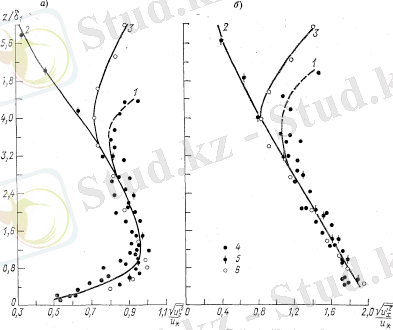
4-сурет. Пульсация жылдамдығы стандарттарының үлестірілімі.
а-вертикальді, б-бойлық; 1-кедір-бұдыр канал, 2-шекаралық қабат, 3-құбырда, 4-автор мәліметтері, 5-С. Коррсин және А. Кистлер бойынша шекаралық қабат пен кедір-бұдыр тақташа мәліметтері, 6-Х. Рейхард бойынша тік құбырдың мәліметтері.
Осы бақылаулар бойынша бойлық пульсация жылдамдығының теріс көп мәндері пульсация симметриялығын санай отырып, оң мәнді пульсациялық жылдамдыөтардың максимумы салынған стандартқа сәйкес деуге болады.
Вертикальді жылдамдық пульсациясы негізгі ағыста аз өзгереді, және ағыс түбіне қарай нольдік мәнде болады, себебі ағыс түбі сұйық бөлшектерінің вертикальді қозғалуына мүмкіндік бермейді. Сондықтан да, айналып ағу мен грунт бөлшектерінің салмағын тексергенде, бойлық жылдамдық пульсацияның әсері басты орында.
Үлестірімнің тақ моменттері жылдамдық пульсациясының ассиметриялы ықтималдылық үлестірілімі сипаттайды. Ішіндегі ең қарапайымы- үшінші орталық момент μ 3 , бұл ассиметрияның өлшемсіз коэффициенті пульсация стандартының кубының үшінші орталық моменттің жеке бөлігін көрсетеді.
Бойлық және вертикаль пульсация үшін түзу және кедір-бұдыр каналдардағы ағыс тереңдігінде әр түрлі орналасқан μ 3 ассиметриялық коэффициент бойынша тәжірибелік мәліметтер 5-суретте көрсетілген. Бойлық және вертикальді пульсацияның ассиметриялығынан алынған мәліметтер ағыс пен арна арасындағы алмасу процессінде ерекше мән ойнайды.
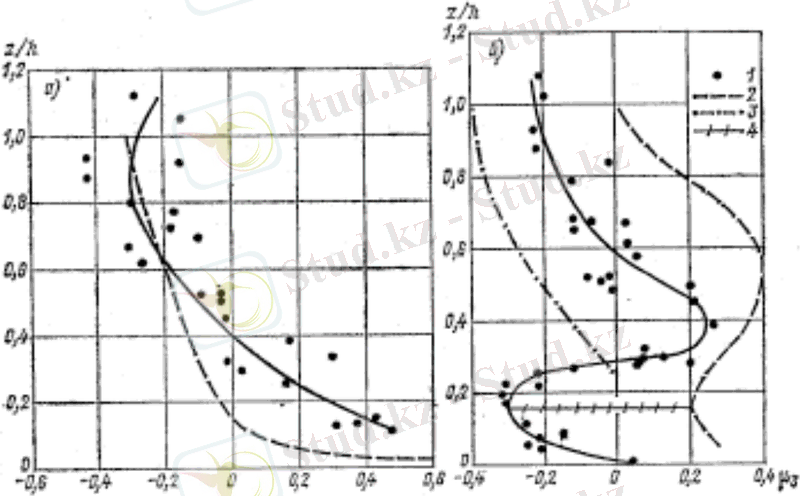
5-сурет. Пульсация ассиметриясының коэффициенті.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz