Дифференциалдық теңдеулер туралы жалпы түсінік

Жоспар
Кіріспе

I. Кіріспе
II. Дифференциалдық теңдеулер туралы жалпы түсінік
1. Бірінші ретті дифференциалдық теңдеулер
1.1 Айнымалылары ажыратылатын теңдеулер
1.2 Біртекті дифференциалдық теңдеулер
1.3 Біртектіге келтірілетін дифференциалдық теңдеулер
1.4 Бірінші ретті сызықтық дифференциалдық теңдеулер.
1.5 Бернулли теңдеуі
1.6 Толық дифференциалды теңдеулер

III. Туындылары арқылы шешілмеген бірінші ретті дифференциалдық теңдеулер
2.1Толымсыз дифференциалдық теңдеулер: y = f(y/) және x = f(y/) түріндегі теңдеулер.
2.2Лагранж және Клеро теңдеулері.
IV. Пайдаланылған әдебиеттер.

Табиғат құбылыстарын зерттегенде, физика жəне техника, химия жəне биология мəселелерін шешкенде, эволюциялық про- цесті анықтайтын шамалар арасындағы тəуелділік, көбіне, шама- лар мен олардың өзгеру жылдамдықтары арасындағы байланыс түрінде, яғни белгісіз функциялар мен туындыларын (дифферен- циалдарын) байланыстыратын теңдеу ретінде алынады. Белгісіз функция жəне оның туындыларын байланыстыратын мұндай теңдеулер дифференциалдық деп аталады. Ізделінді функция бір ғана айнымалыдан тəуелді болса, теңдеу кəдімгі дифференциалдық, ал бірнеше айнымалыдан тəуелді болса, дербес туындылы дифференциалдық деп ата- лады. Мысалы, ең қарапайым кəдімгі дифференциалдық деп, ( ) dy f x dx = теңдеуін айтады, f (x) - белгілі, y = y(x) - ізделініп отырған белгісіз функция. Бұл теңдеудің шешімдерін f (x) фун- кциясының алғашқы функциялары деп атайтындығы белгілі: Жалпы y = ∫ f(x)dx + C шешімдер жиынтығын береді. Массасы m нүктенің F күшінің əсерімен қозғалысы 2 2 , , d r dr m F tr dt dt ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ теңдеуімен беріледі, r - радиус вектор, dr dt - қозғалыс жылдамдығы, 2 2 d r dt - үдеу. Мұндағы ізделінді функция r(t) , ең жоғарғы туындысы - 2. Теңдеу 222 222 4 (, ,) du du du xyz dx dy dz ++= πρ - Пуассон теңдеуі деп аталады, дербес туындылы, ізделінді функция u = u(x, y, z) үш айнымалыдан (x, y, z) тəуелді. 4 Ізделінді функцияның ең жоғарғы туындысы (дифференциа- лы) теңдеудің реті деп аталады. Келтірілген екінші, үшінші мы салдардағы теңдеулер екінші ретті. Теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыра- тын функция теңдеудің шешімі деп аталады. Мысалы, радиоактивтік ыдырау теңдеуінің: ( ) ( ) dx t kx t dt (1) = − шешімі ( ) kt x t Ce − = . (2) С – кез келген тұрақты. Əрине, теңдеу (1) радиоактивті ыды- рау процесін толық анықтамайды. Оны толық анықтау үшін бас- тапқы t0 моментіндегі ыдыраушы заттың х0 мөлшерін білуіміз ке- рек. Егер ( )o o xt x = белгілі болса, радиоактивті ыдырау заңын ( ) kt to o x xe − − = табамыз. Теңдеудің шешімін табуды, дифференциалдық теңдеуді интегралдау деп атайды. Дифференциалдық теңдеуге келтіретін есепті қарастырайық. Массасы m материалдық нүкте салмағының əсерімен құлайды. Ауа кедергісін ескермей, нүктенің қозғалыс заңын табу керек. Шешуі. Нүкте құлайтын О нүктесінен төмен бағытта верти- кал осьті анықтасақ, t - уақытында нүкте y(t) орнында болады. Нүкте салмақ күші əсерімен құлайтындықтан, Ньютонның екінші заңы бойынша ma mg = екендігі белгілі. Мұндағы, үдеу 2 2 , d y a g dt = = онда 2 2 d y m mg dt = теңдеуі нүкте нің қозғалыс заңын анықтайды. Теңдеуді түрлендіріп g, екі рет интегралдау нəтижесінде ше- шімін аламыз. Бұл формула нүктенің қозғалыс заңын береді, бі- рақ екі тұрақты 1 2 C , C бар. Тұрақтыларды 1 2 C , C нүктенің қозғалыс заңын толық анықтау үшін қажетті қосымша шарттардың көмегімен нақтылаймыз. 5 Құлайтын нүктенің, О нүктесіне қарағанда, бастапқы орны 0 y(0) = y жəне бастапқы жылдамдығы 0 ϑ(0) = ϑ белгілі болуы керек. Қозғалыс жылдамдығы ( ) dy t( ) t dt ϑ = болғандықтан C1 = ϑ0 , 2 0 C = y . Сонымен, нүктенің қозғалыс заңын беретін функция 2 0 0 2 gt y ty = ++ ϑ . Бұл, біркелкі үдемелі қозғалыстағы нүктенің жүріп өткен жолы екендігі белгілі. Процестің өтуі туралы толық мағұлмат белгілі болғанда, оның математикалық моделін құруға əрекет жа- салынады. Көп жағдайда, модель дифференциалдық теңдеумен жазылады да, оның бір шешімі процестің функционалдық сипат- таушысы болады. Математикалық ғылым, дифференциалдық теңдеулер теория- сы, процестердің математикалық моделдерін құрып, сипаттаушы функционалдық тəуелділіктерін табумен айналысады.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

Жоспар
I. Кіріспе
II. Дифференциалдық теңдеулер туралы жалпы түсінік
1. Бірінші ретті дифференциалдық теңдеулер
1.1 Айнымалылары ажыратылатын теңдеулер
1.2 Біртекті дифференциалдық теңдеулер
1.3 Біртектіге келтірілетін дифференциалдық теңдеулер
2.4 Бірінші ретті сызықтық дифференциалдық теңдеулер.
2.5 Бернулли теңдеуі
1.6 Толық дифференциалды теңдеулер

III. Туындылары арқылы шешілмеген бірінші ретті дифференциалдық теңдеулер
2.1Толымсыз дифференциалдық теңдеулер: y = f(y) және x = f(y) түріндегі теңдеулер.
2.2Лагранж және Клеро теңдеулері.
IV. Пайдаланылған әдебиеттер.

КІРІСПЕ
Табиғат құбылыстарын зерттегенде, физика жəне техника, химия жəне биология мəселелерін шешкенде, эволюциялық про- цесті анықтайтын шамалар арасындағы тəуелділік, көбіне, шама- лар мен олардың өзгеру жылдамдықтары арасындағы байланыс түрінде, яғни белгісіз функциялар мен туындыларын (дифферен- циалдарын) байланыстыратын теңдеу ретінде алынады. Белгісіз функция жəне оның туындыларын байланыстыратын мұндай теңдеулер дифференциалдық деп аталады. Ізделінді функция бір ғана айнымалыдан тəуелді болса, теңдеу кəдімгі дифференциалдық, ал бірнеше айнымалыдан тəуелді болса, дербес туындылы дифференциалдық деп ата- лады. Мысалы, ең қарапайым кəдімгі дифференциалдық деп, ( ) dy f x dx = теңдеуін айтады, f (x) - белгілі, y = y(x) - ізделініп отырған белгісіз функция. Бұл теңдеудің шешімдерін f (x) фун- кциясының алғашқы функциялары деп атайтындығы белгілі: Жалпы y = ∫ f(x)dx + C шешімдер жиынтығын береді. Массасы m нүктенің F күшінің əсерімен қозғалысы 2 2 , , d r dr m F tr dt dt ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ теңдеуімен беріледі, r - радиус вектор, dr dt - қозғалыс жылдамдығы, 2 2 d r dt - үдеу. Мұндағы ізделінді функция r(t) , ең жоғарғы туындысы - 2. Теңдеу 222 222 4 (, ,) du du du xyz dx dy dz ++= PIρ - Пуассон теңдеуі деп аталады, дербес туындылы, ізделінді функция u = u(x, y, z) үш айнымалыдан (x, y, z) тəуелді. 4 Ізделінді функцияның ең жоғарғы туындысы (дифференциа- лы) теңдеудің реті деп аталады. Келтірілген екінші, үшінші мы салдардағы теңдеулер екінші ретті. Теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыра- тын функция теңдеудің шешімі деп аталады. Мысалы, радиоактивтік ыдырау теңдеуінің: ( ) ( ) dx t kx t dt (1) = − шешімі ( ) kt x t Ce − = . (2) С - кез келген тұрақты. Əрине, теңдеу (1) радиоактивті ыды- рау процесін толық анықтамайды. Оны толық анықтау үшін бас- тапқы t0 моментіндегі ыдыраушы заттың х0 мөлшерін білуіміз ке- рек. Егер ( )o o xt x = белгілі болса, радиоактивті ыдырау заңын ( ) kt to o x xe − − = табамыз. Теңдеудің шешімін табуды, дифференциалдық теңдеуді интегралдау деп атайды. Дифференциалдық теңдеуге келтіретін есепті қарастырайық. Массасы m материалдық нүкте салмағының əсерімен құлайды. Ауа кедергісін ескермей, нүктенің қозғалыс заңын табу керек. Шешуі. Нүкте құлайтын О нүктесінен төмен бағытта верти- кал осьті анықтасақ, t - уақытында нүкте y(t) орнында болады. Нүкте салмақ күші əсерімен құлайтындықтан, Ньютонның екінші заңы бойынша ma mg = екендігі белгілі. Мұндағы, үдеу 2 2 , d y a g dt = = онда 2 2 d y m mg dt = теңдеуі нүкте нің қозғалыс заңын анықтайды. Теңдеуді түрлендіріп g, екі рет интегралдау нəтижесінде ше- шімін аламыз. Бұл формула нүктенің қозғалыс заңын береді, бі- рақ екі тұрақты 1 2 C , C бар. Тұрақтыларды 1 2 C , C нүктенің қозғалыс заңын толық анықтау үшін қажетті қосымша шарттардың көмегімен нақтылаймыз. 5 Құлайтын нүктенің, О нүктесіне қарағанда, бастапқы орны 0 y(0) = y жəне бастапқы жылдамдығы 0 ϑ(0) = ϑ белгілі болуы керек. Қозғалыс жылдамдығы ( ) dy t( ) t dt ϑ = болғандықтан C1 = ϑ0 , 2 0 C = y . Сонымен, нүктенің қозғалыс заңын беретін функция 2 0 0 2 gt y ty = ++ ϑ . Бұл, біркелкі үдемелі қозғалыстағы нүктенің жүріп өткен жолы екендігі белгілі. Процестің өтуі туралы толық мағұлмат белгілі болғанда, оның математикалық моделін құруға əрекет жа- салынады. Көп жағдайда, модель дифференциалдық теңдеумен жазылады да, оның бір шешімі процестің функционалдық сипат- таушысы болады. Математикалық ғылым, дифференциалдық теңдеулер теория- сы, процестердің математикалық моделдерін құрып, сипаттаушы функционалдық тəуелділіктерін табумен айналысады.
Дифференциалдық теңдеулер туралы жалпы түсінік.
y' туындысы интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициенті болады.
Интегралдық қисықтың кез келген А(х, у) нүктесіндегі жанаманың бұрыштық коэффициентін дифференциалдық теңдеуді шешпей-ақ табуға болады.
Жанама интегралдық қисықтың бағытын көрсететін болғандықтан, f(x, y) функциясы үзіліссіз болса А нүктесін үзіліссіз жылжыта отырып, дифференциалдық теңдеуді интегралдау нәтижесінде алынатын қисықтардың бағыттар өрісін көрсетуге болады. Олар теңдеудің жалпы шешімі болады.
Анықтама. Қарастырылып отырған облыстың әрбір нүктесіндегіжанамалар жиынтығы бағыттар өрісі деп аталады.
Жоғарыда айтылғандарды ескере отырып, дифференциалдық теңдеуді геометриялық тұрғыдан талқылайық:
1) Бірінші ретті дифференциалдық теңдеу берілді деген сөз - бағыттар өрісі берілген
2) Дифференциалдық теңдеу шешу не интегралдау дегеніміз - әрбір нүктесіндегі жанамалардың бағыты бағыттар өрісімен беттесетін барлық қисықтарды табу.
Анықтама.Бағыттар өрісінде көлбеулері бірдей қисықтар изоклиндердеп аталады.
Анықтама. Бір немесе бірнеше айнымалы функцияны, тәуелсіз айнымалыларды жəне функцияның туындыларын байланыстыратын теңдеу дифференциалдық теңдеу деп аталады.
Анықтама. Егер ізделінді функция тек бір ғана айнымалыдан тəуелді болса, онда дифференциалдық теңдеу қарапайым деп аталады.
Анықтама.Егер теңдеу бірнеше айнымалыдан тəуелді болып жəне оның осы айнымалылары бойынша алынған дербес туындылардан тұрса, онда дербес туындылы дифференциалдық теңдеу делінеді.
Біз тек қарапайым дифференциалдық теңдеулерді қарастырамыз.
Анықтама. Теңдеудің құрамындағы ең жоғарғы туындының реті дифференциалдық теңдеудің реті деп аталады.
G(x,y,y ′,y′′..., y(п)) = 0 - n-ші ретті дифференциалдық теңдеу десек,
y(п) = F(x,y,y′, y′′,y′′′,...) - бас туындыға қатысты шешілген теңдеу.
Мысалы. у′′+5xу′-x[2]y3= 0 - екінші ретті,
d3ydx3 - xy2 dydx =7 - үшінші ретті,
y′+5xy = cosx - бірінші ретті дифференциалдық теңдеулер.
Анықтама.Дифференциалдық теңдеудің шешімі немесе интегралы деп теңдеуге қойғанда оны тура теңдікке айналдыратын кез келген 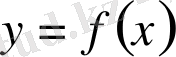функциясын айтады.
Мысал 1. y=sinx функциясы y′′+y=0 теңдеуінің шешімі.
Шынында, берілген теңдеудегі у белгілі, демек у′′-ті анықтайық:
у′ =cosx , у′′= - sinx
Егер y′′, y-ті теңдікке қойсақ: -sinx + sinx =0, яғни 0=0 теңдігіне келдік, демек у= sinx берілген теңдеудің шешімі болады.
Мысал 2. y= x2(1+Ce 1х) функциясы берілсін, мұндағы С - кез келген тұрақты сан. y функциясы х2у′+(1-2х)у= х2 - бірінші ретті дифференциалдық теңдеуінің шешімі болатынын тексерелік.
Ол үшін берілген функцияның бірінші ретті туындысын табайық:

y′= 2x (1+С e 1x) +x[2] (0+С e 1х(- 1x[2]))=2x(1+С e [1]х)-Ce [1х]
у пен у′-ті берілген теңдіктің сол жақ бөлігіне қойсақ:

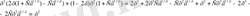
x2=x2тепе-теңдігіне келеміз, яғни берілген функция дифференциалдық теңдеудің шешімі.
Анықтама. Дифференциалдықтеңдеудіңшешімінанық таудифференциалдық теңдеуді интегралдауесебідепаталады.
Анықтама. Егер дифференциалдық теңдеудің шешімі, саны теңдеудің ретіне сəйкес келетін тəуелсіз кез келген тұрақтылардан тұрса, онда ол берілген теңдеудің жалпы шешімі деп аталады.
Мысалы, y= φ (х,С1, С2,..., Сn) n-ші ретті дифференциалдық теңдеудің шешімі.
Жалпы интегралдағы С1, С2,..., Сn тұрақтыларының орнына мəндер қойып дара шешімдер алуға болады.
Мысалы, 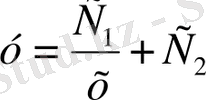функциясы xy'' +2y' =0- екінші ретті дифференциалдық теңдеудің жалпы шешімі болатынын тексерелік.
Шешуі: y ' , y '' - терді тауып теңдікке қоялық:

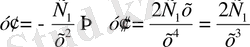
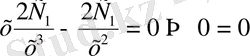, яғнитеңдеуді қанағаттандырады.
Жалпы шешімдегі С1, С2 тұрақтыларға мәндер беріп, дара шешімдер алуға болады: С1=1, С2=0 болғанда ,
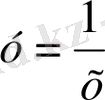С1= -3, С2 =5 болғанда ,
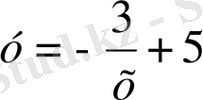С1=0, С2=-1 болғанда .

Анықтама. n-ші ретті дифференциалдық теңдеудің 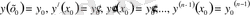- бастапқы деп аталатын шарттарды қанағаттандыратын дара шешімін табу Коши есебі(Огюстен Луи Коши (1789-1857) - француз математигі) деп аталады.
Берілген бастапқы n шартта аргументтің берілген мәніне сәйкес 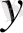функциясының және оның y ' , y '' ,..., y n−1 туындыларының мәні беріледі. Сол шарттардың көмегімен 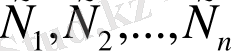тұрақтылардың сәйкес мәндері анықталады.

1 БІРІНШІ РЕТТІ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР
Анықтама.Бірінші ретті дифференциалдық теңдеу дептүріндегі теңдеуді айтады.
Егер бұл теңдік у арқылы шешілсе, яғни 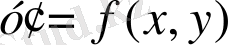түрінде жазылса, онда соңғы теңдеу туындысы арқылы шешілген дифференциалдық теңдеу делінеді.
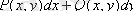- бұл бірінші ретті теңдеудің дифференциалды түрі деп аталады.
Анықтама. Бірінші ретті дифференциалдық теңдеудің жалпы шешімі деп кез-келген бір тұрақты С - дан тәуелді және келесі шарттарды қанағаттандыратын 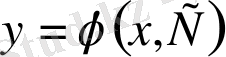функциясын айтады:
а) ол С тұрақтының кез келген мәнінде дифференциалдық теңдеуді қанағаттандырады;
ә) бастапқы шарт х=х0 болғанда у=у0 қандай болмаса да 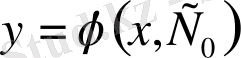функциясы берілген бастапқы шартты қанағаттандыратындай С=С0 мәнін табуға болады ;
Анықтама. Дифференциалдық теңдеудің 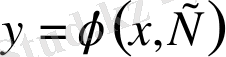жалпы шешіміндегі с тұрақтысына 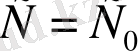мәнін берсеk, онда 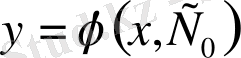- теңдеудің дара шешімі деп аталады.

Дифференциалдық теңдеудің шешімі болатын функция арқылы берілген S қисығы 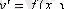теңдеуінің интегралдық қисығы делінеді.

1.1Айнымалылары ажыратылатын теңдеулер

Анықтама. 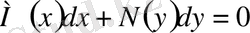- айнымалысы ажыратылған теңдеу, 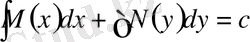- оның жалпы интегралы деп аталады.
Мысалы:

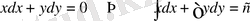
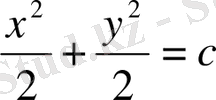
- берілген теңдеудің жалпы интегралы.
Анықтама. 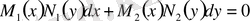- түріндегі теңдеу айнымалысы ажыратылатын теңдеу деп аталады.
Бұл теңдеуді шешу үшін оның екі жағын да 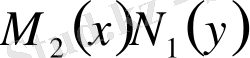көбейтіндісіне бөлеміз. Сөйтіп, айнымалысы ажыратылған теңдеу алуға болады.

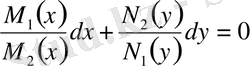
Мысал 1: 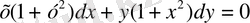теңдеудің интегралын тап:
Шешуі:

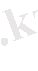
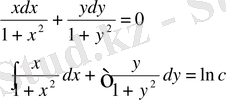
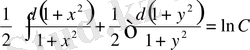
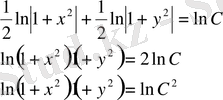
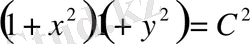- жалпы интеграл.
Мысал 2: 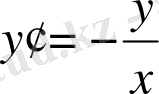дифференциалдық теңдеудің жалпы және дара шешімдерін табайық.

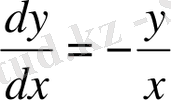
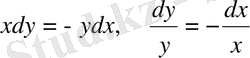
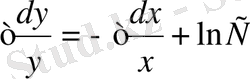
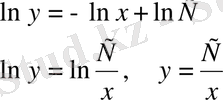
берілген теңдеудің жалпы шешімі. 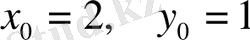болғандағы теңдеудің дара шешімін табатын болсақ: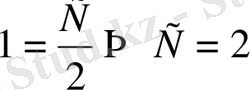. Олай болса, 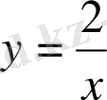берілген теңдеудің дара шешімі.

1.2 Біртекті дифференциалдық теңдеулер
Анықтама. f(x, y) функциясы өзінің х және у аргументтеріне қатысты n-өлшемді біртекті делінеді, егер кез келген t параметрдің (нөлден өзге) мәні үшін келесі тепе-теңдік орындалатын болса: ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.