MATLAB және Maple бағдарламалары: матрицалық есептеулер, дифференциалдық теңдеулер және графиктік визуализацияға кіріспе


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:
Matlab компьютерлік бағдарламасымен танысу.
Matlab - мына сөзден алынған MATrixLABorotory яғни матрицалық лаборатория. Бұл бағдарлама математикалық есептерді электроникалық, радиотехнологиялық және басқа есептерді шығару үшін қолданылады. Оларға матрицалар үшін арналған амалдар қолданылады. Яғни бүкіл математикалық есептер сол матрицалық есептерге арналған. Матловтың негізін өткен ғасырдың 70 жылдары Молер ЭЕМ-ге қолданылады. Ал 80 жылдарға келіп MathWorks, int фирмасының қызметшісі Дж. Литтл РС компьютерлерге жасады.
Матловты орнату үшін кемінде төмендегі конфигурация қажет.
- Pentium 1. 2. 3 IBM 486
- ОЗУ 24 Мбайт
- HDD (қатты диск) 30 Мбайт (кемінде)
- Монитор 256
- Видеокарта
- Adobe Reader немесе Adobe Acrobat
Олар PDF форматтағы файлдарды оқу үшін қолданылады.
Матловтың негізгі операторлары және фукциялары.
Матловта есептер >> мына белгіден басталады.
>> demo демоны жабу немесе [x] >> 2+3 (жауап 5)
>> y=Pi/2
Y 3. 14
>> sin(y)
ans 1
Мысалы: V векторына мән беру керек.
>> V=[273 -1 0. 2] 7
V 273 -1 0. 2
>> W=5*V
W 10 35 +5 -5 3
>> C=
 Equation. 3 (V - векторын квадраттау) .
Equation. 3 (V - векторын квадраттау) .
(V*W.
 Equation. 3 . V*W) дұрыс емес оператор қолдануын қарастырамыз.
Equation. 3 . V*W) дұрыс емес оператор қолдануын қарастырамыз.
- Сондықтан теңдеулер жүйесін шешу.
Мысалы:
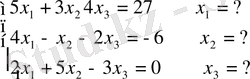
Ах=в Х=В/А
>> A=[5 4 2; 3 -1 5; 4 -2 -3] ;
>> B=[27 -6 0]
B=27
- 6
0
X=B/A
X=1
2
4
Қарапайым дифференциалдық теңдеулер жүйесін шешу.
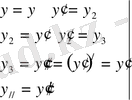
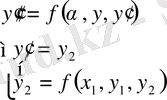
Сөйтіп, к-к дифференциалдық теңдеу төмендегі бірінші реттік дифференциалдық теңдеулер системасына келеді. Бұл алгебралық теңдеудер системасы.
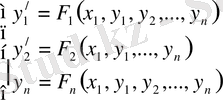
Matlov-та дифференциал теңдеулер жүйесін шешу үшін adl түріндегі командалар қолданылады. Бірақ ол командалар әртүрлі сандық әдебиеттерге негізделген болған үшін олардың әртүрлі варианттары бар. Мысалы:
odl 45. бұл командасы пайдаланған жағдайдағы системаны шешу үшін work папкада Function F=Fn(x, y)
odl 45.
Work (Fn*m)
Function F=Fn(x, y)
F=[F 1 ; F 2 ; …F n ] :
Matlab:
>> [x, y] =abl 45(‘F n ’, [0. 20], [0. 1] )
Y=0
y / =1
мынандай мысалды қарастырамыз
y / 1 =y 2 +0. 02*x 2
y / 2 =-y
Бұл үшін
Function F=F n (x, y)
F=[y(2) +0. 01*
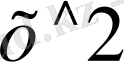 ; -y(1) ] ;
; -y(1) ] ;
Matlab;
>>[x, y] =abl 45(‘F 2 ’[0. 20], [0. 1] ) ;
>>y(:, 1)
Matlab графикасы:
График сызу үшін plat, mesh, surf командасын қолданамыз. Plat - 1 сызық, plat - 3 кеңістігі графигін сызады. мesh - 3 өлшемдік фигура сызады. Мысалы: z=e -x2 -y 2 .
Мұнда фигура тор түрінде болады. Ал, surf командасын пайдаланып алынған фигурада сетка көрінбейді. Ол бүтін беттен тұрады. Ең қарапайым түрде plat (х, у) деп жазылады. Мысалы:
>> x=0: 0. 1:1;
>> y=sin(x) ;
>> plat(x, y)
Графикте әртүрлі түспен және белгілермен сызу үшін.
Plat(x, y, ’z * ’) деп сызуға болады.
Мұндағы: z - графиканың түсін білдіреді.
* - графикалық белгісі.
- сызық * - жұлдызша, + - + сызық, х, нЖ0 - деңгейлік
‘Z * ’ r - қызыл b - көк
C - қара y - сары
g - жасыл.
Дене горизонтал
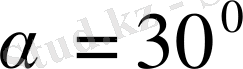 бұрышпен
бұрышпен
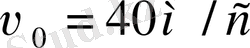 жылдарын лақтырылған, сол дененің ұшу уақытын максимал көтерілу биіктігін және ұшу алыстығын есептеп траекториясын сызу керек.
жылдарын лақтырылған, сол дененің ұшу уақытын максимал көтерілу биіктігін және ұшу алыстығын есептеп траекториясын сызу керек.
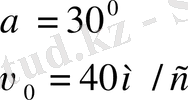

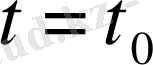 болғанда
болғанда
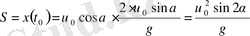
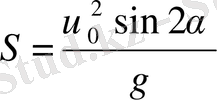
>> V 0 =40; >>g=9. 8
>> alfa=30;
>>alfa = alfa1*Pi/180;
>>tm ==V 0 *sin(alfa) /g
>>t 0 =2*tm
>>h
m
=

>>S=
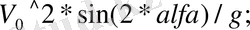
>>t=0:0. 01:t0 >>x =
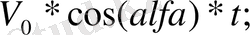
>>Y=
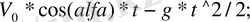
>>Plot (x, y, ’r-’)
x0, hm, ’bo’)
төмендегі қозғалыс теңдеуін шешеміз (тербелмелі қозғалыс)
x // +w 2 x=0 осындай диференциалдық теңдеу болып тербелістің жиілігі W=2.
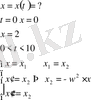
Maple компьютер программасы. Команданың ватерлод (waterloo) жасалған және ол аналитикалық есептерді орындауға арналған. Онда берілген функцияның туындысын есептеу, интеграциялауын есептеу, өрнектерді ықшамдау, теңдеулер, теңсіздіктер, олардың жүйелерін және дифференциалдық теңдеуді шешу графиктер сызу т. б. көптеген амалдарды орындаумен.
Команда және операторлар.
Командамен танысу.
Туынды алу diss(y, x)
>diss(y, x) ;
>y=…
>disf(sin(x) +
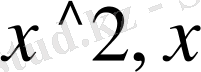 ) ;
) ;
Cos (x) +2x
Келесі операторларды интегралдау.
Int(cos(x) +2x, x) ;
Sin(x) +x 2 анықталмаған интеграл.
Ал анықталған интегралды есептеу үшін
> Int
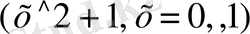
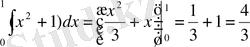
Ықшамдау (берілген өрнекті)
> Simplify (y) ;
Жақшаларды ашып шығу.
> expand (y) ;
Мысалы: > expand ((x+1) *(x-5) ) ;
x 2 -4x-5 нәтижесі
> expand ((x+1) *(x-5), (x+1) ) ) ;
(x+1) x-5(x+1)
Мысалы: >f:=x*y*z+x*y+x*z+y*z;
> simplify (f, {x*z=1}) ;
F; =y+xy+1+yz
Мысалы: >f:=sqrt((x*y)
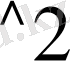 ) ;
) ;
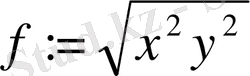
>simplify (f) ;
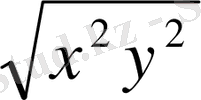
>simplify(s, assume = positive) ;
хy нәтижесі
Көбейткіштерге жіктеу командасы.
> factor(y) ;
Мысалы: > factor (
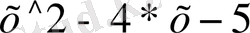 ) ;
) ;
(x+1) (x-5)
Берілген теңдеуді шешу теңсіздіктер, теңдеулер жүйесін шешу.
> solve (y, x) ;
Мысалы: > solve (f=ma, a) ;
 нәтижесі
нәтижесі
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz