Көпөлшемді нормаль үлестірімдер және туынды үлестірімдер: екіөлшемді және n-өлшемді нормаль, оның функциялары, хи-квадрат, Стьюдент, Снедекор-Фишер, Релей, Максвелл және көпномиальді үлестірімдер


Лекция 1.
2 ТАРАУ . КӨПӨЛШЕМДІ ҮЛЕСТІРІМДЕР
Екіөлшемді нормаль үлестірім
Ықтималдықтар теориясы және оның қосымшаларында екіөлшемді нормаль үлестірім үлкен роль атқарады. Екіөлшемді кездейсоқ нормальдың тығыздығы
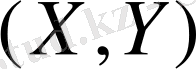 .
.

Бұл үлестірім бес параметрге тәуелді:
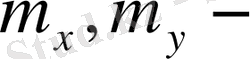 X
және
Y
көлемдерінің математикалық күтімі;
X
және
Y
көлемдерінің математикалық күтімі;
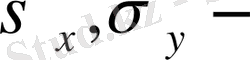 X
және
Y
көлемдерінің орташа квдраттық ауытқуы;
r-
X
және
Y
көлемдерінің орташа квдраттық ауытқуы;
r-
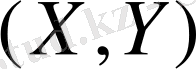 -
X
және
Y
көлемдерінің өзара арақатынас коэфициенті.
-
X
және
Y
көлемдерінің өзара арақатынас коэфициенті.
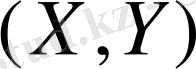 екіөлшемді кездейсоқ нормаль шамалардың компоненттері өзара байланыссыз деп ұйғарайық, сонда
r
=0. Бұдан алатынымыз:
екіөлшемді кездейсоқ нормаль шамалардың компоненттері өзара байланыссыз деп ұйғарайық, сонда
r
=0. Бұдан алатынымыз:
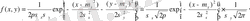
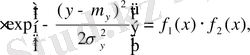
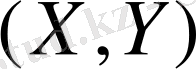 көлемінің тығыздығы
көлемінің тығыздығы
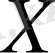 және
және
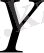 үлестірулерінің тығыздықтарының көбейтіндісіне тең, бұл дегеніміз
үлестірулерінің тығыздықтарының көбейтіндісіне тең, бұл дегеніміз
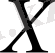 және
және
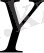 кездейсоқ тәуелсіз көлемдер .
кездейсоқ тәуелсіз көлемдер .
Сонымен келесі теорема дәлелденді:
Кездейсоқ нормальды үлестірім көлемдердің өзара қатыссыздығынан олардың тәуелсіздігі шығады. Сол үшін “ өзара қатыссыз” және “тәуелсіз” терминдері нормальды үлестіруші ушін эквивалентті.
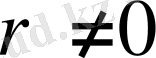 болғанда
болғанда
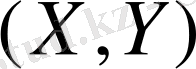 кездейсоқ көлемдері тәуелді.
кездейсоқ көлемдері тәуелді.
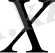 және
және
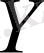 көлемдерінің үлестіруінің шартты заңын былай жазамыз:
көлемдерінің үлестіруінің шартты заңын былай жазамыз:
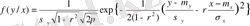 ;
;
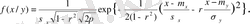
Енді осы екі шартты үлестіру кез келген біреуін талдап көрейік, мысалы
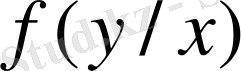 .
.
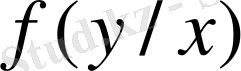 тығыздығының формуласын мына түрде жазамыз.
тығыздығының формуласын мына түрде жазамыз.
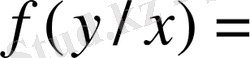
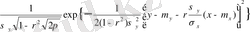 .
.
Сірә, бұл параметрлерімен берілген нормальді үлестіру
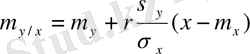
және
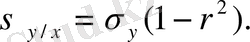
Соңғы екі формула
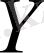 көлемінің шартты заң үлестіруінде X=x тиянақты мәнінде дисперсия тәуелді емес екенін көрсетеді.
көлемінің шартты заң үлестіруінде X=x тиянақты мәнінде дисперсия тәуелді емес екенін көрсетеді.
Көлем
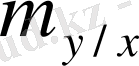 шартты математикалық күтім деп аталады, егер де
шартты математикалық күтім деп аталады, егер де
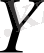 көлемі
көлемі
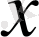 бойынша берілсе.
бойынша берілсе.
Енді нормальды үлестірілген кездейсоқ екіөлшемді көлемнің жазықтықтағы әртүрлі облыстарға түсу ықтималдығының формуласына өтеміз.
Компоненттері тәуелсіз кездейсоқ
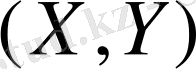 векторы нормальдың заңына бағынышты болсын.
векторы нормальдың заңына бағынышты болсын.
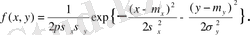
 Енді бізге кездейсоқ
Енді бізге кездейсоқ
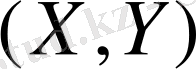 нүктесінің қабырғалары
нүктесінің қабырғалары
 координата осіне параллель болған R тіктөртбұрышына түсу ықтималдығын есептеу шарт.
координата осіне параллель болған R тіктөртбұрышына түсу ықтималдығын есептеу шарт.

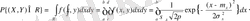
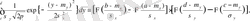
Бұл жерде
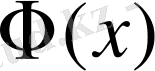 - 0; 1 параметрімен берілген нормальды үлестірім заңының функциясы. Берілген функцияның мәндері тиісті кестеде көрсетілген.
- 0; 1 параметрімен берілген нормальды үлестірім заңының функциясы. Берілген функцияның мәндері тиісті кестеде көрсетілген.
Негізгі түрде есептелуі мүмкін болған түсу ықтималдығы бар кейбір жазық фигуралардың қатарына, тең ықтималды эллипс кіреді.
Жазықтықтағы нормаль заңы үлестірімінің тығыздығы мына түрде берілсін:

Берілген тығыздық эллипсте әрдайым мәндерін сақтап тұрғаны анық:
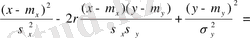

C-тұрақты; осы негізге сүйеніп берілген эллипстер ықтималдықтары тең эллипстер деген атқа ие.
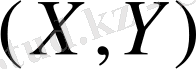 нүктесінің
нүктесінің
 тең ықтималды эллипстің ішіне түсу ықтималдығын табайық.
тең ықтималды эллипстің ішіне түсу ықтималдығын табайық.
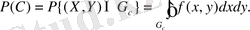
Берілген интегралды есептеу үшін полярлық координаталарды енгіземіз:
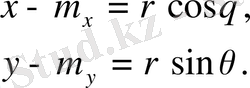
Бұл жағдайда соңғы интеграл мына түрде болады:

Ықшамдап белгілесек
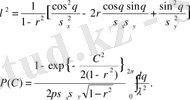
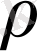 бойынша интегралдағанда жоғарыдағы сөйлем шығады.
бойынша интегралдағанда жоғарыдағы сөйлем шығады.
 бойынша интегралдауды тригонометриялық функцияларды интегралдау ережесімен орындауға болады, бірақ бұл аса қажет емес, себебі ол автоматты түрде ықтималдықтың түсінігі көмегімен көбейтіледі. Шынында да,
бойынша интегралдауды тригонометриялық функцияларды интегралдау ережесімен орындауға болады, бірақ бұл аса қажет емес, себебі ол автоматты түрде ықтималдықтың түсінігі көмегімен көбейтіледі. Шынында да,
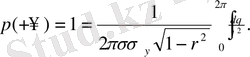
Бұдан
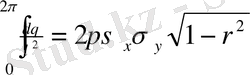
Олай болса
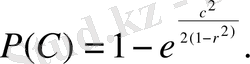
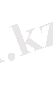
Мысалы. Кездейсоқ
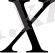 және
және
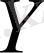 көлемдері тәуелсіз және
көлемдері тәуелсіз және
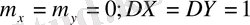
пен нормальді үлестірілсе. Кездейсоқ
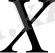 және
және
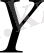 нүктелерінің
нүктелерінің
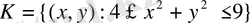 сақинасына түсу ықтималдығын табу керек.
сақинасына түсу ықтималдығын табу керек.
Шешуі.
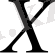 және
және
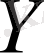 кездейсоқ көлемдері тәуелсіз сондықтан олар өзара қатыссыз, олай болса r=0. Анық болғандай
кездейсоқ көлемдері тәуелсіз сондықтан олар өзара қатыссыз, олай болса r=0. Анық болғандай
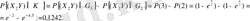
Лекция 2
 2. n-өлшемді нормальді үлестірімнің жалпы жағдайы
2. n-өлшемді нормальді үлестірімнің жалпы жағдайы
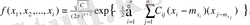
Мұнда
 , өзара қатысты
, өзара қатысты
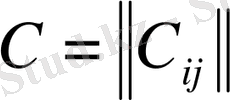 матрицаға кері матрицаның анықтауышы;
матрицаға кері матрицаның анықтауышы;
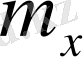 -
-
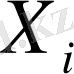 n өлшемді кездейсоқ нормальді вектордың математикалық күтімі.
n өлшемді кездейсоқ нормальді вектордың математикалық күтімі.
Жалпы сөйлемнен, барлық нормаль заңының өлшеудің кезкелген санына және кездейсоқ көлемдер арасындағы кезкелген тәуелділік үшін болған формасы шығады. Сонымен қатар n=2 болғанда өзара қатысты матрица былай
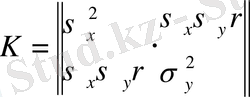 ,
,
r- өзара қатыстық коэфиценті. Бұдан
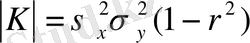 ;
;
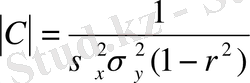
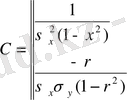

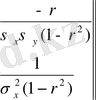
Матрица анықтауышы
 ны және оның мүшелерін жалпы формулаға қою арқылы жазықтықтағы нормаль заңының формуласын аламыз.
ны және оның мүшелерін жалпы формулаға қою арқылы жазықтықтағы нормаль заңының формуласын аламыз.
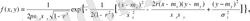
Бұл формула 1 тараудың басында барілген болатын.
Егер де кездейсоқ
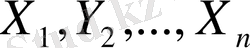 көлемдері тәуелсіз болса, онда көлемдері
көлемдері тәуелсіз болса, онда көлемдері
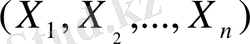 болатын үлестірімнің тығыздығы мынаған тең:
болатын үлестірімнің тығыздығы мынаған тең:
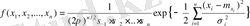
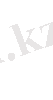 n=1 болғанда бұл формула мына түрге келеді:
n=1 болғанда бұл формула мына түрге келеді:
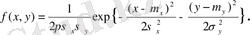
Лекция 3
3 Тарау . Нормальді үлестірілген кездейсоқ көлемдердің функциясы. хи-квадрат, Стьюдент, Снедекор- Фишер үлестірімі.
Ең жай функция бұл -сызықтық функция, сондықтан да алдымен нормаль заңына бағынышты екі кездейсоқ тәуелсіз көлемдерді қарастырамыз.
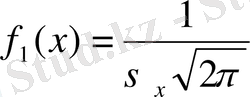
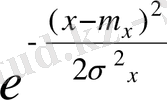 ,
,
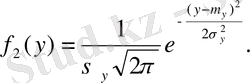
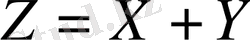 үлестірім қосынысының тығыздығын табамыз. Үлестірім заңының үйлесімділігі үшін жалпы формуланы пайдаланамыз:
үлестірім қосынысының тығыздығын табамыз. Үлестірім заңының үйлесімділігі үшін жалпы формуланы пайдаланамыз:
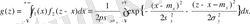
Соңғы интегралды есептеп мынаны аламыз:
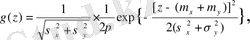
 Ал бұл мынадай параметрлермен алынған нормаль заңынан басқа ештеңе де емес
Ал бұл мынадай параметрлермен алынған нормаль заңынан басқа ештеңе де емес
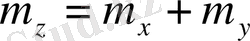
 және
және
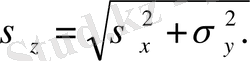
Сопымен біз келесі ережеге тоқталамыз.
Нормальды үлестірімнің құрылысының ережесі: Нормальды үлестірімнің құрылысынан қайтадан нормальды үлестірім пайда болады, әрі математикалық күтім мен дисперсиялар қосындыланады.
Енді бұған кері мақұлдаудың бар екенін байқаймыз.
Крамер теоремасы: егер де кездейсоқ екі тәуелсіз көлемдердің қосындысы нормаль заңы бойынша үлестірілсе, онда әрбір қосылғыш нормаль заңымен үлестіріледі.
Нормальды үлестірімнің ережесі кездейсоқ тәуелсіз көлемнің әйтеуір бір кез келген саны үшін жалпылануы мүмкін.
Егер де
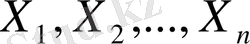 көлемдердің n бар болса, орташа
көлемдердің n бар болса, орташа
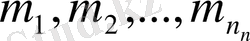 және де
және де
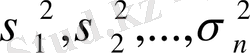 дисперсияларымен, онда
дисперсияларымен, онда
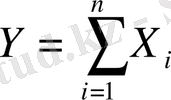 көлемі төмендегі параметрлермен берілген нормаль үлестірімге ие болады
көлемі төмендегі параметрлермен берілген нормаль үлестірімге ие болады
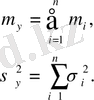
Енді тәуелді қосылғыштардың жағдайына көшеміз.
Егер кездейсоқ
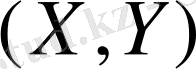 вектор нормаль үлестірімді болса, және оның
X
және
Y
компоненттері тәуелді, онда олардың қосындыларын үлестірудің заңы
Z=X+Y
орташасы бар нормаль заңы болып табылады.
вектор нормаль үлестірімді болса, және оның
X
және
Y
компоненттері тәуелді, онда олардың қосындыларын үлестірудің заңы
Z=X+Y
орташасы бар нормаль заңы болып табылады.
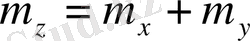
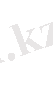
және мына дисперсиялармен
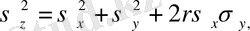
Мұндағы r- көлемдердің корреляция коэффициенті.
Жалпы жағдайды қарастырайық: нормальды үлестірілген аргументтен алынған сызықты функцияны.
n
- өлшемді кездейсоқ
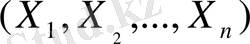 көлемі берілген,
Y
кездейсоқ көлем мына көлемдердің сызықтық функциясын көрсетеді.
көлемі берілген,
Y
кездейсоқ көлем мына көлемдердің сызықтық функциясын көрсетеді.
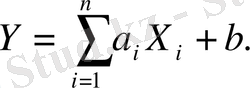
Кездейсоқ Y көлемі тағы да нормальды үлестіріліп тұрғаны анық көрініп тұр.
Математикалық күтім мен дисперсияның қасиеттерін пайдаланып Y кездейсоқ көлемін есептеуге болады:
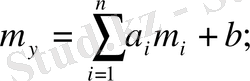
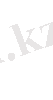
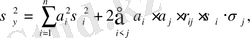
Мұндағы
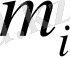 -
-
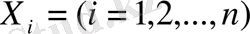 кездейсоқ көлемнің математикалық күтімі.
кездейсоқ көлемнің математикалық күтімі.
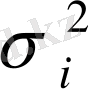 -
-
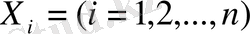 көлемінің дисперпесиясы;
көлемінің дисперпесиясы;
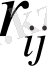 -
-
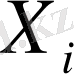 және
және
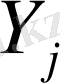 арасындағы корелляция коэффициенті.
арасындағы корелляция коэффициенті.
Лекция 4
n - еркін дәрежелі хи-квадрат үлестірім.
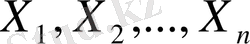 - кездейсоқ тәуелсіз көлемдері параметрлері
- кездейсоқ тәуелсіз көлемдері параметрлері
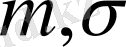 нормаль заңымен үлестірілген.
нормаль заңымен үлестірілген.
Көлемді үлестірудің формуласы
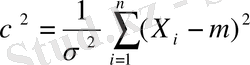
n- дәрежелі хи- квадрат үлестірім деп аталады.
Кездейсоқ көлемнің
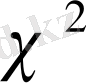 -екі еркін дәрежелі үлестірімі бар тығыздығын табамыз. бұл жерде
-екі еркін дәрежелі үлестірімі бар тығыздығын табамыз. бұл жерде
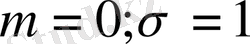 қоямыз.
қоямыз.
Алдымен
 кездейсоқ нормальды үлестірілген үлестірімнің квадрвтын табамыз.
кездейсоқ нормальды үлестірілген үлестірімнің квадрвтын табамыз.
y>0 болғандағы үлестірім функциясынан аламыз .
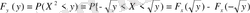
Бұл жерден

Сірә,
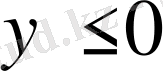 болғанда
болғанда
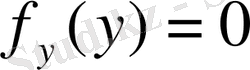 тең.
тең.
Енді үлестірім тығыздығының қосындысын табамыз
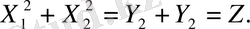 z >0 болғанда аламыз
z >0 болғанда аламыз
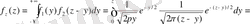
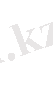


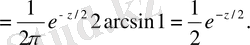
Сонымен
 - үлестірімінің тығыздығы
- үлестірімінің тығыздығы
 еркіндік дәрежесімен мынаған тең:
еркіндік дәрежесімен мынаған тең:
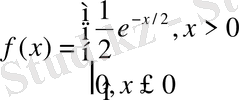
n
еркіндік дәрежесімен берілген
 - үлестірімінің тығыздығы х>0 болғанда мына түрге ие:
- үлестірімінің тығыздығы х>0 болғанда мына түрге ие:
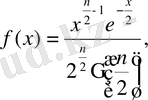 мұндағы
мұндағы
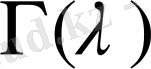 - гамма - функция.
- гамма - функция.
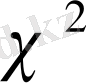 - үлестірімінің мәні таблицада берілген.
- үлестірімінің мәні таблицада берілген.
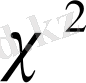 -үлестірімінің
n
еркідік дәрежесімен алынған математикалық күтімі
n
ге тең, ал дисперсиясы 2
n
ге тең.
-үлестірімінің
n
еркідік дәрежесімен алынған математикалық күтімі
n
ге тең, ал дисперсиясы 2
n
ге тең.
Релей және Максвелл үлестірімдері
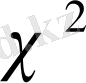 -үлестірімімен өзара тығыз байланысты.
-үлестірімімен өзара тығыз байланысты.
Релей үлестірімі
координаттары жазықтықтағы декарттық координаталар жүйесінде тәуелсіз және 0 және
 параметрлерімен берілген нормаль үлестірімі бар кездейсоқ вектордың ұзындығының үлестірімімен түсіндіріледі десе болады.
параметрлерімен берілген нормаль үлестірімі бар кездейсоқ вектордың ұзындығының үлестірімімен түсіндіріледі десе болады.

 болғандағы Релей үлестірімі екі еркін жәрежесі бар
болғандағы Релей үлестірімі екі еркін жәрежесі бар
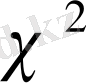 -үлестірімді кездейсоқ көлемнен алынған квадрат түбір үлестірімімімен дәл сәйкес келеді.
-үлестірімді кездейсоқ көлемнен алынған квадрат түбір үлестірімімімен дәл сәйкес келеді.
Релей үлестірімінің тығыздығы :
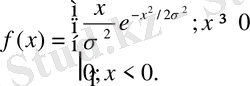 ,
,
Максвелл үлестірімі
координаттары үшөлшемді кеңістіктегі декарттық координаталар жүйесінде тәуелсіз және 0 мен
 параметрлерімен нормальданған кездейсоқ вектор ұзындығының үлестірімімен түсіндіріледі.
параметрлерімен нормальданған кездейсоқ вектор ұзындығының үлестірімімен түсіндіріледі.

 болғандағы Мааксвелл үлестірімі үш еркін жәрежесі бар
болғандағы Мааксвелл үлестірімі үш еркін жәрежесі бар
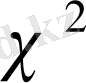 -үлестірімді кездейсоқ көлемнен алынған квадрат түбір үлестірімімімен дәл сәйкес келеді
-үлестірімді кездейсоқ көлемнен алынған квадрат түбір үлестірімімімен дәл сәйкес келеді
Максвелл үлестірімінің тығыздығы мынадай :
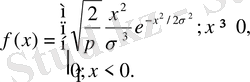
Максвелл үлестірімі статистикалық механикада және физикада бөлшектердің жылдамдығының үлестірімі ретінде кең мәлім.
Стьюдент үлестірімі S t(n) [Стьюдент- ағылшын статистігі Госсеттің лақаб аты, ол бірінші болып осы заңды эмпирикалық жолмен тапқан] .
Стьюдент үлестірімі n еркіндік дәрежесімен төмендегі қатынаспен анықталады:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz