Сызықтық теңдеулер жүйесі: анықтамалар, шешу әдістері (Крамер, кері матрица, Гаусс, Жордан-Гаусс) және Кронекер-Капелли теоремасы


Сызықтық тендеулер жүйесі.
Жоспар:
1. Жалпы ұғымдар және анықтамалар.
2. n белгісізі бар n сызықтық теңдеулер жүйесін Крамер әдісімен шығару.
3. n белгісізі бар n сызықтық теңдеулер жүйесін кері матрица және Жордан-Гаусс әдісімен шешу.
4. n белгісізі бар m сызықтық теңдеулер жүйесін зерттеу Кронекер-Капелли теоремасы.
1. Жалпы ұғымдар мен анықтамалар.
n белгісізі бар n сызықты теңдеулер жүйесі берілсін делік:
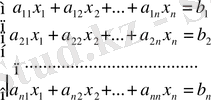
(1)
Мұндағы,
a
ij
- кез келген нақты сандар;
x
i
- белгісіз шамалар; ал
b
i
- бос мүшелер;
i=
(
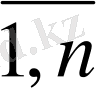 )
; j=
(
)
; j=
(
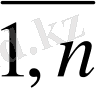 ) .
) .
Берілген жүйедегі a ij - осы жүйенің коэффициенттері, ал b i бос мүшелері деп аталады. Сызықты теңдеулер жүйесіндегі b 1 , b 2 , …, b n бос мүшелерінің кем дегенде біреуі нөлге тең болмаған жағдайда, жүйені біртекті емес сызықты теңдеулер жүйесі деп атайды. b 1 , b 2 , …, b n бос мүшелерінің бәрі нөлге тең болса, онда ол біртекті сызықты теңдеулер жүйесі деп аталады.
Анықтама. Егер x 1 =α 1 , x 2 =α 2 , …, x n =α n - сандар жиыны теңдеулер жүйесіндегі теңдеулердің бәрін қанағаттандырса, онда осы сандар жиыны (1) сызықты теңдеулер жүйесінің шешімі деп аталады.
Егер (1) - сызықты теңдеулер жүйесінің кем дегенде бір шешімі бар болса, онда ол үйлесімді жүйе , ал егер бірде бір шешімі болмаса (жоқ болса), онда ол үйлесімсіз жүйе деп аталады.
Сонымен, үйлесімді жүйенің тек бір ғана шешімі немесе бірден көп шешімі бар. Тек бір ғана шешімі бар жүйе анықталған жүйе деп аталады. Кем дегенде екі шешімі бар жүйе анықталмаған жүйе деп аталады. Егер екі теңдеулер жүйелерінің шешімдері бірдей болса, онда ол теңдеулер жүйелерін тең күшті деп атайды.
2. n белгісізі бар n сызықтық теңдеулер жүйесін Крамер әдісімен шығару.
n белгісізі бар біртекті емес сызықты теңдеулер жүйесін қарастырайық:
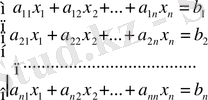
(1)
Бұл жүйенің белгісіздер саны теңдеулер санына тең, жүйенің негізгі матрицасы n жатық, n тік жолдардан тұрады. Сондықтан жүйенің негізгі матрицасы n-ретті квадрат матрица болады.
A=
(2)
А матрицаның анықтауышы берілген сызықты теңдеулер жүйесінің бас анықтауышы деп аталады.
(1) жүйенің анықтауышы нөлге тең болмасын, яғни
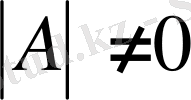 .
.
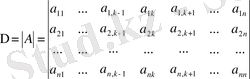 (1) жүйенің бас анықтауышы
(1) жүйенің бас анықтауышы
Берілген жүйенің бас анықтауышының бірінші тік жолының элементтері
x
1
белгісіздің коэффициенттері, ал екінші тік жолдың элементтері
x
2
белгісіздің коэффициенттері т. с. с. Осы анықтауыштың кез келген тік жолының, мысалы
к
-тік жолының элементтерін (
x
к
белгісізінің коэффициенттерін) (1) жүйенің сәйкес бос мүшелерімен орын алмастырғанда алынған анықтауышты
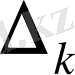 таңбасымен белгілейік:
таңбасымен белгілейік:
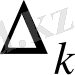 =
=
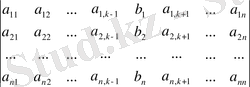 к
=(
к
=(
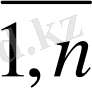 )
)
Крамер теоремасы . Егер (1) біртекті емес сызықты теңдеулер жүйесінің негізгі матрицасының анықтауышы нөлге тең болмаса, онда ол анықталған жүйе. Бұл жүйенің шешімі Крамер формуласымен анықталады:
x
k
=
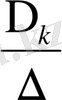 ,
k=(
,
k=(
 )
(3)
)
(3)
(3) - Крамер формулалары деп аталады.
Мысал. Крамер формулаларын қолданып мына жүйені шешіңіз:
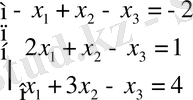
Шешімі:
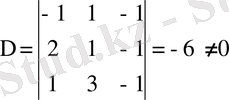
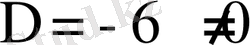 , берілген жүйе - анықталған, оның бір ғана шешуі бар.
, берілген жүйе - анықталған, оның бір ғана шешуі бар.
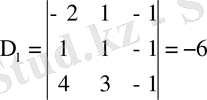 ;
;
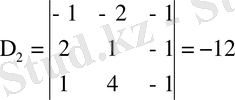 ;
;
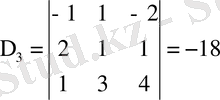
x
1
=
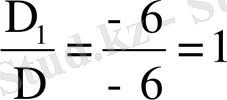 x
2
=
x
2
=
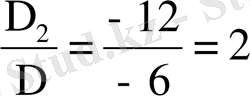 x
3
=
x
3
=
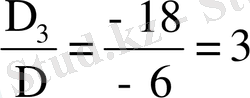 n белгісізі бар n сызықтық теңдеулер жүйесін кері матрица және Жордан-Гаусс әдісімен шешу
n белгісізі бар n сызықтық теңдеулер жүйесін кері матрица және Жордан-Гаусс әдісімен шешу
Жауабы: x 1 = 1; x 2 = 2; x 3 = 3.
3. n белгісізі бар n сызықтық теңдеулер жүйесін кері матрица және Жордан-Гаусс әдісімен шешу .
Кері матрица әдісі .
Берілген (1) жүйені кері матрица әдісімен шешу үшін осы жүйенің төмендегі матрицаларын қарастырайық:
A =
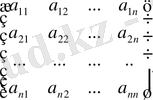 ; Х =
; Х =
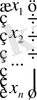 ; B =
; B =
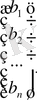 ;
;
Мұндағы
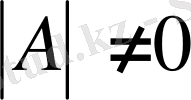 болсын, Х - белгісіз
n
болсын, Х - белгісіз
n
 1 өлшемді матрица.
1 өлшемді матрица.
Матрицаларға қолданылатын амалдарға сүйене отырып, А мен Х матрицаларының көбейтіндісі (1) жүйенің сол жағындағы өрнектен анықталған матрицаға тең деп аламыз. Алдымен А мен Х матрицаларының көбейтіндісін анықтайық:
А*Х =
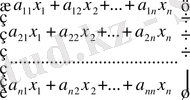
А*Х пен В матрицаларының теңдігінен мына теңдеуді аламыз:
А*Х = В; (4)
Мұндағы, Х - белгісіз
n
 1 матрица және
1 матрица және
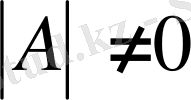 (4) теңдеу (1) жүйенің
матрица түріндегі теңдеуі
деп аталады.
(4) теңдеу (1) жүйенің
матрица түріндегі теңдеуі
деп аталады.
Берілген жүйенің матрицасы ерекше емес матрица, сондықтан оның кері матрицасы бар.
Енді (4) теңдеудің шешімін табу үшін осы теңдеуді солдан оңға қарай А матрицасының кері матрицасына көбейтейік:
А -1 *А*Х=А -1 *В
Мұндағы, А -1 *А=Е және Е*Х=Х. Олай болса
Х=А -1 *В (5)
болады, мұндағы А -1 *В - көбейтіндісі бар.
Мысал. Матрица әдісімен төмендегі жүйені шешіңіз.
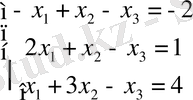 немесе А*Х=В - берілген жүйенің матрицалық түрі.
немесе А*Х=В - берілген жүйенің матрицалық түрі.
Шешімі: Алдымен А, В, Х матрицаларын жазайық:
А=
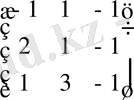 ; В=
; В=
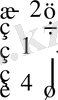 ; Х=
; Х=
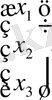
Мұндағы
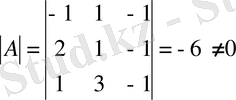 ,
А матрицаның кері А
-1
матрицасы бар.
,
А матрицаның кері А
-1
матрицасы бар.
Енді А матрицасының кері матрицасын анықтайық.
А
11
=
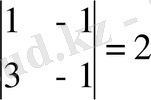 А
21
=
А
21
=
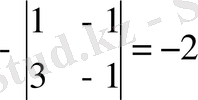 А
31
=
А
31
=
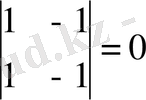
А
12
=
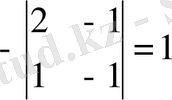 А
22
=
А
22
=
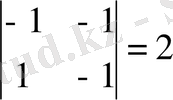 А
32
=
А
32
=
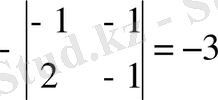
А
13
=
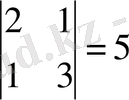 А
23
=
А
23
=
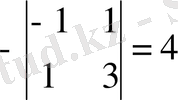 А
33
=
А
33
=
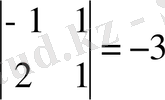
Онда кері матрица А -1 тең болады:
А
-1
=
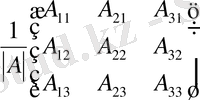 Equation. 3
Equation. 3
А
-1
=
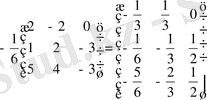 Equation. 3
Equation. 3
Енді (5) формула арқылы Х табамыз:
Х = А -1 *В
Х =
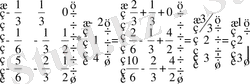 Equation. 3
Equation. 3
Сонымен, Х =
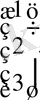 , немесе
, немесе
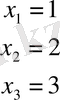
Жауабы: х 1 = 1, х 2 = 2, х 3 = 3.
Белгісіздерді біртіндеп жою әдісі (Гаусс әдісі) .
Сызықты n белгісізді n теңдеулер жүйесін Крамер ережесімен шешкенде n-ші ретті n+1 анықтауышты есептеуге тура келеді. Ол оңай жұмыс емес. Енді белгісіздерді біртіндеп жою әдісі деп аталатын (Гаусс әдісі) әдісті қарастырайық.
Теңдеулер жүйесі берілсін:
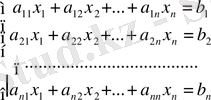
(1)
Белгісіздер x i коэффициенттерінің арасында нөлден өзгешесі бар деп ұйғарайық. Мысалы, ол a 11 коэффициенті болсын делік. Оны шешуші элемент деп атаймыз. Жүйенің бірінші теңдеуін a 11 -ге бөлеміз.
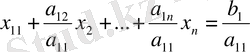
Осы теңдеуді a 21 -ге көбейтіп екінші теңдеуден аламыз. Содан кейін a 31 -ге көбейтіп үшінші теңдеуден аламыз, т. с. с. Осы операциялар көмегімен, екінші теңдеуден бастап, барлық теңдеулерде x 1 -ді жоямыз. Осы сияқты x 2 -ні де жоямыз, т. с. с.
Сонымен (1) теңдеулер жүйесін үшбұрышты түрге келтіреміз:
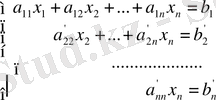
Егер
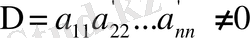 болса, соңғы теңдеуден
болса, соңғы теңдеуден
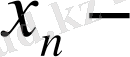 ді табамыз. Одан жоғары теңдеуге қойып
ді табамыз. Одан жоғары теңдеуге қойып
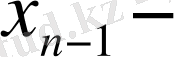 ді табамыз, т. с. с. Ең соңғы
ді табамыз, т. с. с. Ең соңғы
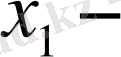 ді табамыз.
ді табамыз.
Егер (1) жүйенің анықтауышы нөлге тең болса, онда жүйе үйлесімді болмайды немесе анықталмаған болады.
Гаусс әдісін қолданғанда түрленген жүйені қайта-қайта көшіріп жазудың қажеті жоқ. (1) -ші жүйенің кеңейтілген матрицасын көшіріп жазып, сол матрицаны түрлендіру керек.
Мысал 1. Теңдеулер жүйесін Гаусс әдісімен шешу керек.
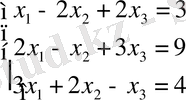
Жүйенің кеңейтілген матрицасын құрайық:
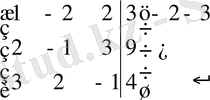 ~
~
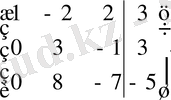 ~
~
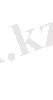
х 1 x 3 x 2 х 1 x 3 x 2
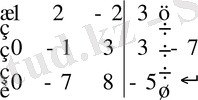 ~
~
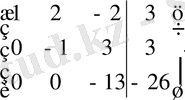
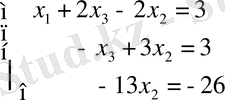
Үшінші теңдеуден:
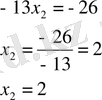
Екінші теңдеуден:
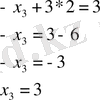
Бірінші теңдеуден:
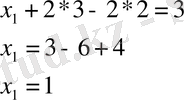
Сонымен жүйенің шешуі:
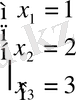
Тексеру:
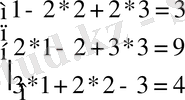
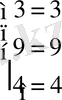
Жауабы:
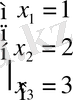
Мысал 2.
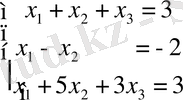
Шешуі:
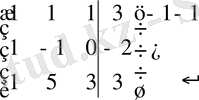 ~
~
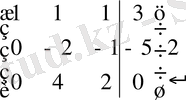 ~
~
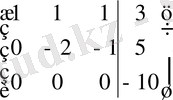
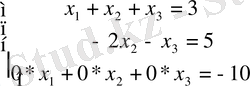 яғни 0 = -10. Сондықтан, берілген теңдеулер жүйесі үйлесімсіз (шешуі жоқ) .
яғни 0 = -10. Сондықтан, берілген теңдеулер жүйесі үйлесімсіз (шешуі жоқ) .
Гаусс әдісінің модификациясы - Жордан-Гаусс әдісі және оның алгоритмі.
Жордан-Гаусс әдісі Гаусс әдісінің модификациясы болып табылады. Бұл әдіс бірнеше қадамдардан тұрады.
1 қадам. Жүйедегі қолайлы бір теңдеуді алып, оны шешуші теңдеу деп атаймыз.
2 қадам. Шешуші теңдеуден алдындағы коэффициентті нөлге тең емес бірге тең болса тіпті қолайлы, айнымалыны таңдап аламыз.
Айнымалының алдында бірге тең коэффициент алу үшін теңдеуді мүшелей айнымалы алдында тұрған санға бөлеміз. Таңдап алынған коэффициентті шешуші элемент деп атаймыз.
3 қадам. Таңдап алынған айнымалыны шешуші теңдеуден басқасынан арылтамыз.
4 қадам. Жүйедегі теңдеулерден біртіндеп айнымалыларды арылту үшін 1 - 3 қадамдарды қайталаймыз да ең соңынан есептің шешуін немесе жүйенің шешуі болмайтындығын көрсетеміз.
Жордан-Гаусс әдісімен сызықтық теңдеулер жүйесін шешуді кестеде орындайды.
- Шешуші жол шешуші элементке бөлінеді.
- Жаңа кестеде шешуші коэффициент бірге тең болып тік жолдағы элементтер нөлге толтырылады.
- Егер шешуші жатық жолда (тік жолда) нөлдер болса, онда оларға сәйкес тік жолдар (жатық жолдар) өзгеріссіз жазылады.
- Басқа элементтері «төртбұрыш» ережесімен есептеледі.
В С
С - шешуші элемент
А Д А
жаңа
=
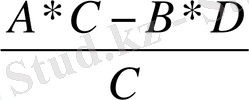 Equation. 3
Equation. 3
Мысал 3. Берілген үшінші ретті жүйені Жордан-Гаусс әдісімен шығарайық.
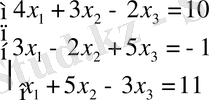
Шешуі: Жүйеде үш белгісіз бар, үш теңдеулер жүйесі бар. Әрбір теңдеу бірақ рет шешу теңдеу болады. Сондықтан жүйені шешу үшін төрт кесте құру керек.
a 31 = 1 - шешуші элемент
1 кесте
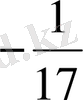 ( )
( )
a 12 = -17 - шешуші элемент
2 кесте
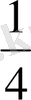
( ) a 23 = 4 - шешуші элемент
3 кесте
4 кесте
Сонымен,
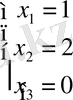
Жауабы:
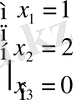
Мысал 4.
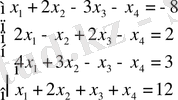
Шешуі: Бұл жүйені шешу үшін бес кесте құрамыз.
a 11 = 1 - шешуші элемент
a 44 = 2 - шешуші элемент
 ( )
( )
 a
33
= 5 - шешуші элемент
a
33
= 5 - шешуші элемент
( )
a 22 = 1 - шешуші элемент
Сонымен, х 1 = 1
х 2 = 2
х 3 = 3
х 4 = 4
Жауабы:
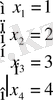
4. n белгісізі бар m сызықтық теңдеулер жүйесін зерттеу Кронекер-Капелли теоремасы.
n белгісізі бар біртекті емес m сызықты теңдеулер жүйесін қарастырайық:
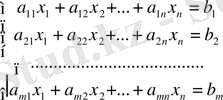
(1)
Берілген жүйенің негізгі матрицасының рангісі мен оның кеңейтілген матрицасының рангісі арасында
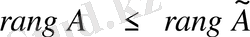
байланыстары бар, мұндағы
 жүйенің негізгі матрицасы, яғни
жүйенің негізгі матрицасы, яғни
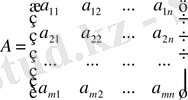 болады, ал
болады, ал
 жүйенің кеңейтілген матрицасы
жүйенің кеңейтілген матрицасы
 болады.
болады.
Берілген жүйені зерттеу немесе үйлесімді немесе үйлесімсіз болатынын айқындайтын Кронекер-Капелли теоремасы.
Теорема. (Кронекер-Капелли)
Біртекті емес (1) сызықты теңдеулер жүйесі үйлесімді болу үшін жүйенің негізгі матрицасының рангісі оның кеңейтілген матрицасының рангісіне тең болуы:
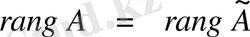 қажетті әрі жеткілікті.
қажетті әрі жеткілікті.
Мұнда екі жағдайды қарастыруға болады:
Бірінші жағдай:
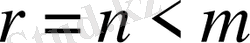
Бұл жағдайда (1) жүйе мына түрде жазылады:
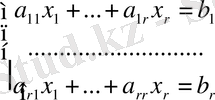 (2)
(2)
Егер де
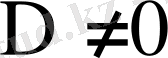 ескерсек, онда жүйенің шешімі
ескерсек, онда жүйенің шешімі
 тек біреу ғана және ол Крамер формуласымен анықталады. Бұл шешу (1) жүйенің қалған
тек біреу ғана және ол Крамер формуласымен анықталады. Бұл шешу (1) жүйенің қалған
 теңдеулерін қанағаттандырады. Сонымен, (1) жүйе
үйлесімді
және
анықталған.
теңдеулерін қанағаттандырады. Сонымен, (1) жүйе
үйлесімді
және
анықталған.
Екінші жағдай:
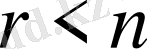 . Бұл жағдайда (1) жүйені мына түрде жазуға болады:
. Бұл жағдайда (1) жүйені мына түрде жазуға болады:
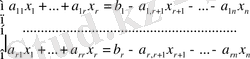 (3)
(3)
Мұндағы,
 белгісіздер бос мүшелер. Олар кез келген тұрақты сандарды қабылдайды. Енді
белгісіздер бос мүшелер. Олар кез келген тұрақты сандарды қабылдайды. Енді
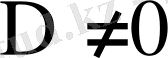 ескеріп, Крамер формуласын пайдаланып, (3) жүйенің де шешімін
ескеріп, Крамер формуласын пайдаланып, (3) жүйенің де шешімін
 анықтаймыз. Сонымен, (1) жүйе
үйлесімді
. Бұл шешім
анықтаймыз. Сонымен, (1) жүйе
үйлесімді
. Бұл шешім
 арқылы өрнектелгендіктен, (1) а
нықталмаған
жүйе, яғни оның шексіз көп шешімі бар. Сонымен, Кронекер-Капелли теоремасы мына төмендегідей қорытындыға келтіреді:
арқылы өрнектелгендіктен, (1) а
нықталмаған
жүйе, яғни оның шексіз көп шешімі бар. Сонымен, Кронекер-Капелли теоремасы мына төмендегідей қорытындыға келтіреді:
- Егер, онда (1) жүйенің тек бір ғана шешімі бар;
- Егерболса, онда (1) жүйенің шексіз көп шешімі бар және ол шешімдер (3) жүйеден анықталады. (3) жүйеден анықталғаншешімі (1) жүйеніңжалпы шешімідеп аталады.
Егер
 айнымалы шамаларға кез келген сандық мәндерді берсек, онда оның жалпы шешімінен жүйенің
дербес шешімін
анықтаймыз. (3) жүйенің
айнымалы шамаларға кез келген сандық мәндерді берсек, онда оның жалпы шешімінен жүйенің
дербес шешімін
анықтаймыз. (3) жүйенің
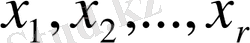 коэффициенттерінен анықталған
коэффициенттерінен анықталған
 (4)
(4)
анықтауыш (3) жүйенің негізгі миноры деп аталады.
Берілген (1) жүйенің шешімін табу үшін мына ережені пайдаланған тиімді:
- Жүйенің үйлесімді не үйлесімсіз болатынын анықтау керек. Ол үшін негізгіматрица мен кеңейтілгенматрицаның рангілерін табу қажет.
- Егер жүйе үйлесімді болса:, ондаретті (4) негізгі минорды қарастырамыз. негізгі минордың коэффициенттері арқылы анықталғантеңдеуді аламыз, ал қалғантеңдеулерді емес, яғни (3) жүйені қарастырамыз, мұндағы- белгісіздер, ал- бос мүшелер.
- Жоғарыда қарастырылған әдістермен (Крамер, Гаусс, Жордан-Гаусс, матрица әдістері) берілгенбелгісізі бар біртекті емессызықты теңдеулер жүйесінің шешімін табамыз.
Мысалдар. Төмендегі жүйелерді зерттеп, олардың шешімдерін табыңдар:
1)
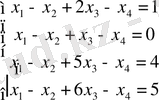 2)
2)
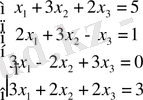
3)
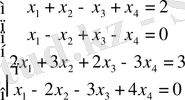
Шешімдері:
1) Берілген жүйенің негізгі
 матрицасы мен кеңейтілген
матрицасы мен кеңейтілген
 матрицасының рангілерін табамыз:
матрицасының рангілерін табамыз:
 ~
~
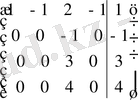 ~
~
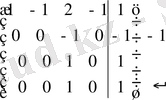
~
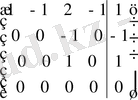 ~
~
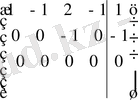 ;
;
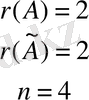
Сонымен,
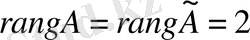 . Олай болса Кронекер-Капелли теоремасы бойынша берілген жүйе үйлесімді, бірақ анықталмаған, оның шексіз көп шешімі бар.
. Олай болса Кронекер-Капелли теоремасы бойынша берілген жүйе үйлесімді, бірақ анықталмаған, оның шексіз көп шешімі бар.
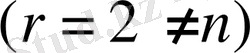 . Осы жүйенің жалпы шешімін табайық.
. Осы жүйенің жалпы шешімін табайық.
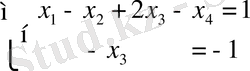
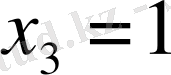
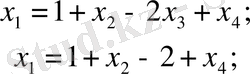
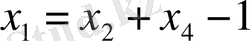
Берілген жүйенің жалпы шешімі:
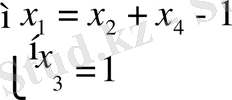
Енді жүйенің кез келген бір дербес шешімін табу үшін
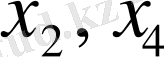 -ке, мысалы,
-ке, мысалы,
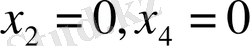 қойамыз:
қойамыз:
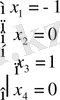 - жүйенің бір дербес шешімі.
- жүйенің бір дербес шешімі.
Осы сияқты, берілген жүйенің басқа да дербес шешімдерін табуға болады.
2) Берілген жүйенің негізгі және кеңейтілген матрицаларының рангілерін табайық:
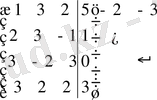 ~
~
 ~
~
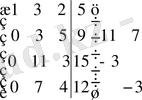 ~
~
 ~
~
 ~
~

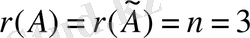 . Бұл жүйе үйлесімді және анықталған. Оның тек бір ғана шешімі бар.
. Бұл жүйе үйлесімді және анықталған. Оның тек бір ғана шешімі бар.
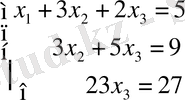
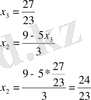
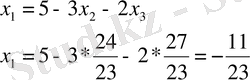
Сонымен, жүйенің шешімі:
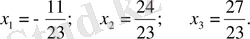
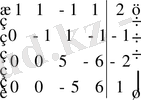
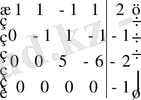
3) Берілген жүйені Кронекер-Капелли теоремасы арқылы зерттейік.
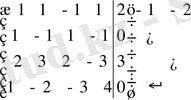 ~
~
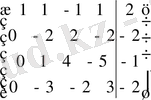 ~
~

 ~
~
 ;
;
Берілген жүйенің
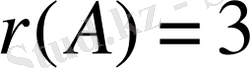 ;
;
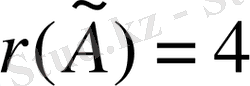 ;
;
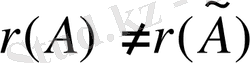 .
.
Сондықтан, берілген жүйе үйлесімсіз (шешімі жоқ) .
Біртекті сызықты теңдеулер жүйесі.
n белгісізі бар біртект і m теңдеулер жүйесі берілсін:
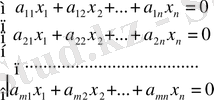
(5)
немесе
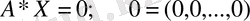
Берілген (5) жүйенің
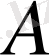 мен
мен
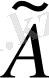 матрицасының рангісі тең, себебі
матрицасының рангісі тең, себебі
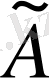 матрицасының соңғы тік жолының барлық элементтері нөлге тең.
матрицасының соңғы тік жолының барлық элементтері нөлге тең.
Сонымен, Кронекер-Капелли теоремасы бойынша берілген (5)
біртекті
жүйе әрқашан да үйлесімді және оның әрқашан да нөлдік шешімі бар:
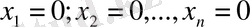 . Ал бізге (5) жүйенің нөлдік шешімнен өзге шешімдерін табу қажет.
. Ал бізге (5) жүйенің нөлдік шешімнен өзге шешімдерін табу қажет.
(5) жүйенің рангісі
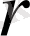 -ге тең болсын деп ұйғарайық:
-ге тең болсын деп ұйғарайық:
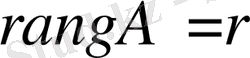 . Анықтық үшін
. Анықтық үшін
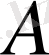 матрицасының алғашқы
матрицасының алғашқы
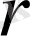 жатық жолы сызықты тәуелсіз болсын.
жатық жолы сызықты тәуелсіз болсын.
Теорема 1.
(5)
біртекті
сызықты теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін
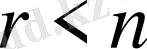 теңсіздігінің орындалуы қажетті әрі жеткілікті.
теңсіздігінің орындалуы қажетті әрі жеткілікті.
Теорема 2.
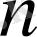 белгісізі бар
белгісізі бар
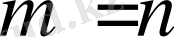 біртекті
сызықты теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін жүйенің анықтауышы нөлге тең болуы:
қажетті әрі жеткілікті.
біртекті
сызықты теңдеулер жүйесінің нөлден өзге шешімдері бар болуы үшін жүйенің анықтауышы нөлге тең болуы:
қажетті әрі жеткілікті.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz