А.А. Фридманның космологиялық модельдеріне сыни және математикалық талдау


« А. А. Фридманның әлем кеңістігінің модуліне сыни көзқарас»
тақырыбындағы
БІТІРУ ЖҰМЫСЫ
ҚЫСҚАРҒАН СӨЗДЕР МЕН ШАРТТЫ БЕЛГІЛЕУЛЕР
АСТ Арнайы салыстырмалылық теориясы
ЖСТ жалпы салыстырмалылық теориясы
СБЕ моделі стационарлы, біртекті, евкллитті моделі
с Жарық жылдамдығы, мәні 2, 998⋅10 10 см/с
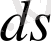 Екі нүктенің ара қашықтығы. (интервал)
Екі нүктенің ара қашықтығы. (интервал)
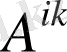 2-рангілі, контравариантты тензор
2-рангілі, контравариантты тензор
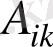 2-рангілі, ковариантты тензор
2-рангілі, ковариантты тензор
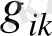 2-рангілі, ковариантты метрикалық тензор
2-рангілі, ковариантты метрикалық тензор
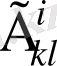 Кристоффель символдары
Кристоффель символдары
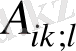 Коварианттық туынды
Коварианттық туынды
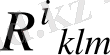 Қисықтық тензоры немесе Риман тензоры
Қисықтық тензоры немесе Риман тензоры
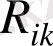 Ричи тензоры
Ричи тензоры
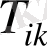 Энергия - импульс тензоры
Энергия - импульс тензоры
РЕФЕРАТ
Бітіру жұмысы 45 бет, 3 бөлім, 3 суреттен тұрады. Қолданылған әдебиеттер саны 20. Қосымшалар саны 1.
Кілт сөздер: Арнайы салыстырмалылық теориясы, жалпы салыстырмалылық теориясы, Фридман моделі, кеңеюші әлем.
МАЗМҰНЫКіріспе5
1 Эйнштейнге дейінгі космологиялық моделдер және олардың қиыншылықтары7
2 Арнайы және жалпы салыстырмалылық теориясы11
2. 1 Арнайы салыстырылмалық теориясы және оның элементтері11
2. 2 Жалпы саыстырмалылық теориясының элементтері16
2. 3 Эйнштейннің космологиялық әлемі24
3 А. А. Фридманның стационарлы емес космологиясы26
3. 1 Фридманның әлем модельдері26
3. 2 Фридманның космологиялық теңдеуі29
3. 3 Жабық изотроптық модель32
3. 4 Ашық изотроптық модель33
Қортынды36
Қолданылған әдебиеттер тізімі37
Қосымша А39
КІРІСПЕҒалам эволюциясы - физика ғылымының теориялық базисіне және көптеген астрофизикалық бақылауларға негізделіп дәлелденген ғылыми факт.
Ғалам эволюциясы жайлы қазіргі заман ғылымының негізін өзінің 1915 ж. Жасаған жалпы салыстырмалылық теориясы негізінде 1917 жылы Альберт Эйнштейн салып кеткен. Ол жұлдыздармен бірқалыпты толтырылған әлем үшін теңдеу құрып, кеңістіктің қисаюы ақырында өзіне өзі тірелетіндігін есептеп шығарды. Осындай “тұйық” ғаламның көлемі шектелген болып, оның шекаралары болған жоқ. Бірақ Эйнштейннің бұл теориясында бір кемшілік болды, яғни осы теория шынайы болған жағдайда жұлдыздар тартылыс күшінің әсерімен бір нүктеге жиналып қалуға тиіс болды. Сол себепті Эйнштейн ғаламды бір-біріне сығылуынан сақтайтын, әлдебір “антигравитациялық” өрісті ойлап табуға мәжбүр болып, теңдеуін осы өріспен толықтырды [1, 2] .
Эйнштейннің моделі сол кездегі жалпы салыстырмалылық теориясының (ЖСТ) негізінде әлемнің уақыт бойынша өзгермейтінін түсіндіретін бірден бір модель сияқты көрінді. Ресей математигі Александр Фридман 1922 - 1924 жылдары жарық көрген еңбектерінде бұл проблеманың жалғыз статикалық емес, сонымен қатар динамикалық та шешімдері бар екендігін дәлелдегенде Эйнштейн бұл көзқарасты жоққа шығаруға тырысып, теріс қабылдады [3, 4, 5, 6] . Фридманның түсіндіруінше қисық қеңістік стационар болуы мүмкін емес, ол ұлғайуы немесе сығылуы керек. Кейінірек Фридманның түсінік берілген жеке хатынан кейін ол кешірім сұрайды. Ғаламның стационарлы еместігі жайлы теория тек 1929 жылы, яғни алдымен астроном В. М. Слайфер, ал одан кейін Э. Хаббл кө птеген бақылаулардың нәтижесінде ғаламның кеңеюі фактісін анықтағанда ғана дәлелденді [7] . Атап айтсақ: Сол кездегі бақылаулар негізінде біздің галактикадан басқа да көптеген галактикалар табылды, олардың бір біріне салыстырмалы қозғалатыны байқалған. Доплер эффектісі арқылы алыс қашықтықтағы жұлдыздардың бізден салыстырғанда радиалды қозғалысы бақылаулар арқылы зерттелді, сосын галактикалардың қозғалысы бақыланды. Сараптау, зерттеу нәтижелері негізінде, егер жұлдыздар бізге қарай қозғалса олардың спектрлік сызықтары күлгін түске ығысатыны, ал керісінше, бізден алыстаса қызыл түске ығысатыны тұрақтандырылған. Бізден алыс галактикаларды зерттеу таңғалдырарлық нәтижелер берді. Барлық галактикалардың спектрлері қызы түске қарай ығысқан. Бұл дегеніміз, бізден барлық галактикалар алыстап бара жатыр дегенді білдіреді. Ал қызыл ығысудың шамасы мен галактикалардың қашықтау жылдамдығы алыс галактикаларда үлкен болған, басқаша айтқанда, галактика қанша алыс орналасса, соншалықты тез алыстап бара жатыр. Қарапайым мысал айтсақ, біз ауа толтырылған шарды алайық, оның беті біртекті қара дақтармен толтырылсын, бақылаушы бір қара дақта тұр десек, онда ең алыс қашықтықта орналасқан қара дақ сол бақылаушы қара даққа жақын орналасқан дақтардың алыстау жылдамдығына қарағанда тез болады. Бұндай нәтиже басқа дақтарда тұрып бақыласа да байқалады. Сонымен біртекті ұлғаю барысында барлық қара дақтардың арақашықтығы ұлғаяды. Сол себепті қызыл ығысуды өлшеу әлемнің кеңейіп бара жатқандығының дәлелі бола алады. Ал ұлғаю жан-жаққа бірдей болып, әлемнің қақ ортасын белгілеу мүмкін емес. Әрине осыдан кейін әлем не үшін кеңейеді? Әлем жалғасты ұлғая бере ма? Галактика қалай және неден түзілген деген сұрақтардың болары анық. Хаббл ғаламның кеңеюін дәлелдегенде ғана, Г. Гамовтың айтысуынша, Эйнштейн өзінің көзқарасының теріс екендігі мойындап “бұл менің өмірімдегі ең үлкен қателік” деп жариялаған [8] .
Бұл бітіру жұмысында, әлемyнің кеңеюі теориясының бастауы болған Фридманның моделін және ол туралы сынды көзқарастар қарастырылады. бүгінгі әлем турлы түсініктің қалай екендігін сараптаймыз, математикалық тұрғыдан maple 18 программасы арқылы ЖСТ аясында осы моделдік есептерді қарастырамыз.
1 эйнштейнге дейінгі космологиялық моделдер және олардың қиыншылықтарыБүкіл әлем және оның қашан, қалай пайда болғандығы туралы мәселелер ежелден бері адамзатты толғандырып келе жатқан маңызды мәселелер болып табылады.
Әлемнің әр түрлі космологиялық моделдері осындай сұрақтардың негізінде пайда болған еді. Бұл арада әлем туралы анықтаманы бере кеткен жөн. Әлем дегеніміз - адамзат эмпирикалық бақылау жасай алатын, адамзат мекендеген кеңістік. Ал әлемнің дамуын зерттеу астрономияның бір бөлігі болып саналатын космология ғылымының негізгі мақсаттарының бірі. Яғни космология әлемнің қалай пайда болғанын ғана емес келешекте қалай дамитындығына да жауап беру керек. Сондықтан космология қазығы заманғы жаратылыстану ғылымдарының ең маңыздыларының бірі болып саналады.
Жалпы космология ғылымы әлемді ұлкен масштаптарда зерттеумен айналысады. Қазырғы космологиялық қашақтақ пен уақыт шамамен10 28 см және 3 10 17 с.
Космологилық зерттеулер нәтижесінде әлем дамуының және пайда болуының көптеген моделдері жарыққа шықты. Бырақ нақтылы касмологиялық моделді құрастыру тек 1916 жылы Альберт Эйнштейн жалпы салыстырмалылық теориясын ашқаннан кейін ғана мүмкін болды.
Егер тарихқа көз жіберер болсақ, космология ерте заманның өзінде ақ астрономияның маңызды болігі болғанын көре аламыз. Бәрінен гөрі Демокриттің, Пифагордың, Аристотельдің (б. з. б. 5-4 ғ-ларда) ежелгі дәуірдегі философия мектептерінің Космологиялық көзқарастары қатаң логикалық талаптарды қанағаттандырды. Астрономия, т. б. жаратылыстану білімдерінің жинақталуы нәтижесінде және Ғалам туралы әр түрлі философия пайымдаулардың негізінде дүние құрылымын тұтас алып қарастырудың ең алғашқы әрекеті - дүниенің геоцентрлік жүйесі (Птолемей) жасалды. Бұл жүйенің негізгі Космологиялық идеялары: Жер қозғалмайды әрі ол Ғаламның кіндігі, Ғалам кеңістік бойынша шектелген, «аспан» мен «жердің» табиғаты бір-бірінен мүлдем алшақ. Кейінірек (16 ғ-да) астрономия мен жаратылыстану ғылымында төңкеріс болған дүниенің гелиоцентрлік жүйесі (Н. Коперник) жасалды.
Птоломей мен Коперниктің «әлемдік жүйесі» ілімі сол кездегі космологиялық жұйенің әлем туралы көрінісі болып табылады. Тіпті Кеплер 1618-1622 ж. ж шыққан «Коперник астрономиясының қысқаруы » атты кітабында күнді жұлдыздар сферасының ( жүлдызды сфера мұз бен кристалдан тұрады) ортасына орналастырған. Кеплер алемнің шегарасы деп санаған осы сфераға дейінгі ара қашықтықты 60млн жер радиусына тең деп есептеген [9] .
Қазырғы кезде арине мұндай арақашықтықтың бізге ең жақын орналасқан жұлдыздың арақащықтығынан жұз есеге аз екні белгілі. Шындығында Джордано Бруно 1600 жылдың өзінде ақ әлемнің шексіздігі және жұлдыздардың санының шексіздігі туралы идея ұсынған еді. Әрине сол кезде мұндай идея ешкімнен қолдау таппаған, тіпті сол кездің ұлы астрономы Кеплер де бұл идеяны терістеген.
1609 ж . Галилейден бастау алатын телескопиялық астрономияның дамуы, әлемнің шексіздігі туралы моделді дәлелдеді деуге болады. Ең кемінде сол кездегі астрономия әлемнің мұндай моделіне қарсы келмеді. XIX ғасырдың алғаш рет В. Гершельдің (1738-1822) жұлдыздарды және тұмандықтарды зерттеуі нәтижесінде біздің жұлдыздық жүйемізбен (галактикамызбен) басқада жұлдыздық жұиелер (галактикалар ) туралы тұсініктер тереңдей түсті.
Жалпы космологиялық мәселелер физиканың гравитациялық құбылысымен, оны зерттейтін тарауымен тығыз байланысты, үйткені дүниежүзілік әлемді құрастырып тұрған заттардың, физикалық объектілердің бәрі өзара бірін-бірі гравитациялық күштердің әсерімен тартады. Бұл - табиғи құбылыс. Осы құбылыстың, басқаша айтқанда, гравитациялық құбылыстың ғылыми теориясын ең алғаш соны құрастырып, негізгі заңдарын аналитикалық формулаларын тағайындап берген ағылшын ғалымы - физигі Иссак Ньютон.
Оның 1687 жылы жарық көрген Табиғат философияның математикалық бастамалары (латынша: «Philosophiæ Naturalis Principia Mathematica») деген кітабы ғылым тарихындағы ең ықпалды шығарма болып саналады. Осы еңбегінде Ньютон бүкіләлемдік тартылыс заңын және қозғалыс заңдарын тұжырымдап, содан кейінгі үш ғасырда үстемдік еткен және қазіргі заманғы инженерлік ғылымның негізі болып табылатын классикалық механиканың негізін қалады. Ньютон өзінің тартылыс заңы мен Кеплердің ғаламшарлар қозғалысының заңдарының арасындағы сәйкестікті дәлелдеп, жер бетіндегі заттардың қозғалысы мен аспан денелерінің қозғалысы бірдей заңдарға бағынатынын көрсетті. Осылайша ол гелиоцентризм туралы соңғы күмәнды сейілтіп, ғылыми революцияның басын бастап берді.
Бұл құбылыстар математикалық тұрғыдан үш өлшемді жазып евклид кеңістігінде баяндалады. Осы көзқарас бойынша, кеңістік дегеніміз ішінде Ньютонның бүкіл әлемдік тартылыс күштерінің әсерімен механикалық қозғалыстар өтіп жататын сыртқы жай ғана үш өлшемді евклид кеңістігін еске түсіреді, оның заттардың таралуына, тығыздығына, қозғалыс күйіне ешқандай қатысы жоқ ыдысты елестеді, ал уақытша еш нәрсеге тәуелсіз өз бетімен өтіп жатқан процестің ұзақтығын елестетеді. Заттардың қозғалыс заңдылықтары Ньютонның классикалық механикасына бағынады.
Галактикадан сыртқы астрономия, яғни басқада галактикаларды зерттеу, тек біздің ғасырда ғана дами бастады.
Ал XIX ғасырдағы әлемнің нақтылы моделін айтар болсақ, ол кеңестік бойынша шексіз және біртекті, уақыт бойынша өзгермейтін космологиялық модель болып табылады. Бұл модельдің кеңестігі әрине евклитті болып саналады. Өйткені сол кездегі космологияда оның қасиеттерін зерттеуде Ньютонның бүкіләлемдік тартылыс күшін ғана негізге алған. Ньютонның бүкіл әлемдік тартылыс күші - стационарлы, уақытша тәуелсіз, кеңістік евклид геометриясына қанағаттандырады, олардың ішінде ерекше қасиеті бар арнайы нүкте жоқ деп есептелінеді. Сол себепті кеңістік қасиеттері біртекті. Бізді қорғаушы бүкіл әлемдік кеңістікті басқаша елестетуге ғалымдарда басқа негіз жоқ еді.
Деседе бұл космологиялық модельдің бір қанша қиындықтары болды.
Солардың біріншісі (Ольберс парадоксы деп аталады) стационарлы, біртекті, евкллитті моделге (СБЕ моделі) сәйкес, бүкіл аспан күн сияқта жарық сәуле шығаруы керек.
Біздің біртекті кеңістігіміз қаптаған саны шексіз жұлдыздарға толы. Сол кеңістікте жұлдыздар бір қалыпты (тығыздылығы «n» тұрақты) орналасқан екен десек, онда ені Δr қабаттағы жұлдыздар саны
 - ға тең.
r
- сақинасының радиусы.
- ға тең.
r
- сақинасының радиусы.
Содан келетін жарықтың күші
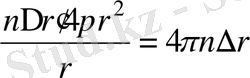
Олай болса кеңістіктегі барлық жұлдыздардан келетін жарық күші,
, басқаша айтқанда, әлем жап-жарық болып тұру керек. Шынында олай еместігі мәлім. бұны фотомейрлік (оптикалық) парадокс деп атайды.
Бұл қиындық жұлдыздардың әлемге біртекті таралмағанын немесе керісінше кеңестіктің шексіз еместігін көрсетеді.
Екінші қиындық СБЕ моделіне термодинамика заңдарын қолдануға байланысты туындады. Егер әлем стационарлы және шексіз өмір сүрсе, онда әлемдегі денелердің бәрі әлде қашан «тыныштықта» яғни өзінің тепе теңдіктегі күйіне келген болар еді. Бұл парадоксты ашқан неміс физигі К. Нейман (1874 ж. )
Үшінші қиындық Зеелигер парадоксы деп аталады. Бұл қиындық СБЕ моделіне Ньютонның бұкіл әлемдік тартылыс заңын қолдануға байланысты.
Яғыни кез келген дененің (М 1 ) екінші денемен (М 2 ) Ньютонның бүкіл әлемдік теориясы бойынша
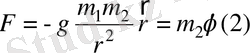 , (1. 1)
, (1. 1)
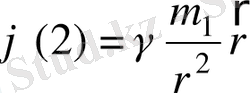 .
.
Бірінші дененің екінші дене орналасқан жердегі потенциалы. Ол нақты анықталмаған ал денелер орналасқан әлемдегі жалпы гравитациялық потенциалдың нақты шамасы (мәні) белгісіз. Бұл гравитациялық парадокс деп аталады.
Осы жерде мынадай өте маңызды жағдайға көңіл бөлелік: біз қарастырып жатқан теория Ньютонның гравитациялық теориясы деп аталады. Ол дұрыс, үйткені оны ашқан, жасаған адам ол- Ньютон. Оның негізінде Ньютонның бүкіләлемдік тартылыс күші жатыр,
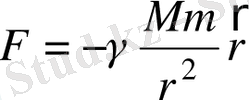 , (1. 2)
, (1. 2)
мұнда М - гравтация өрісін туғызатын орталық дененің массасы, ол гравитация өрісінің көзі, m -сынақ денесінің массасы, γ- Ньютондық тартылыс тұрақтысы . Гравитациялық күштің шамасы, мәні өзара әсерлесетін денелердің арақашықтығының квадратына кері пропорция. Ол электродинамикадағы Кулон күшіне ұқсас.
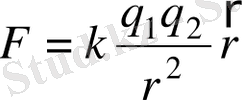 (1. 3)
(1. 3)
Кулон күші электро статика өрістік туғызатыны мәлім. Ньютон күші, олай болса грави статика өрісін туғызады. Ньютонның гравитатциялық теориясы тек қана гравистатика.
Әрі қарай бұл теорияны электродинамика пәнімен салыстырайық. Электродинамикада электростатикадан кейін Джеймс Клерк Максвелл 1831 жылы М. Фарадей ашқан индукция заңына сүйене отырып, басқаша айтқанда, айнымалы магнит өрісі айнымалы құйынды электр өрісін туғызады, содан түпкісінде табиғатта біріккен айнымалы электромагниттік өріс реальды түрде орын алады. Осыған сай келетін теорияны, оның дифференциалды теідеулерін 1861 - 1883 ж. ж. Дж. Максвелл тауып берді, көптеген электро магниттік құбылыстар түсіндірілді. Ол теорияны әрі қарай дамытқан нидерланд ғалымы Х. Лоренц болды. Ол өзінің заттардың электрондық теориясы арқылы, ең бастысы, жарықтың еркін электромагниттік толқын екендігін, жарықтың заттармен әсерлесу құбылыстарын толық түсіндіріп берді.
Енді өзіміз қарастырып жатқан СБЕ моделіне қайта оралайық. Жоғарыда айтып өткен парадокстардан кейін СБЕ моделі тығырыққа тірелді деуге болады. Қалай болмасын, Эйнштейін космологиясына дейін бұл қиыншылықтарды шешіу мүмкін болмады.
ХХ ғасырдың басында жалпы салыстырмалылық теориясының ашылыу космологияның дамуы мен жаңа космологиялық моделдің пайда болуына түрткі болды.
Жалпы салыстырмалылық теориясын космологияға қолдану 1917 ж. Эйнштейіннен бастау алған еді. Біз төменде Эйнштейіннің космологиялық моделін қарастырмас бұрын салыстырмалық теориясы турылы кейбір түсініктерді қарастырамыз.
2 арнайы және жалпы салыстырмалылық теориясыЖалпы салыстырмалылық теориясы космостық масштабтарда қарастырылатын әлем қасиеттеріне байланысты мәселелерді шешу жолындағы жаңа мүмкіндіктерді ашты. Мұнда пайда болатын тамаша мүмкіндіктер кеңістік-уақыттың галилейлік еместігімен байланысты
Жалпы салыстырмалылық теориясы аясындағы әлемнің моделі Эйнштейн теңдеулерімен түсіндірілетіндіктен, Эйнштейн теңдеулеріндегі тенорлық шамалардың қасиеттерін қарастыруға тура келеді.
Жалпы салыстырмалылық теориясы уақыт пен кеңістіктің және гравитацияның теориясы, бұл теорияны 1915 ж. өзінің арнайы салыстырмалылық теориясы негізінде (АСТ) Эйнштейні құрастырды.
2. 1 Арнайы салыстырылмалық теориясы және оның элементтеріКез-келген дененің қозғалысы жөнінде оны басқа денелермен салыстыра отырып ғана айтуға болады. Әдетте бұл басқа денелермен қандай да бiр санақ жүйесiн байланыстырады да, қозғалысты осы санақ жүйесiне қатысты қарастырады. Механикадағы Ньютонның заңдары орынды болатын санақ жүйелерiн инерциалды санақ жүйелерi деп атайды. Берiлген инерциалды санақ жүйесiне қатысты бiрқалыпты түзусызықты қозғалып бара жатқан кез-келген басқа санақ жүйесi де инерциалды болады, яғни ол жүйелерде де Ньютон заңдары орынды. Барлық инерциалдық жүйелерiнде механикалық құбылыстар бiрдей болып өтедi. Бұл тұжырым Галилейдiң салыстырмалылық принципi деп аталады. Математикалық тұрғыдан алғанда бұл принцип механика заңдарының кез-келген инерциалды санақ жүйесiнде бiрдей теңдеумен сипатталатынын көрсетедi
Ендi мынадай заңды сұрақ туындылайды: салыстырмалылық принципі тек механикалық процесстер үшін ғана орынды ма, жоқ әлде басқа құбылыстар үшін де орындала ма? Басқаша айтқанда, мысалы, электромагниттік құбылыстар әртүрлi инерциалды санақ жүйелерiнде бiрдей өте ме? Бұл сұрақтың жауабы бiз ойлағандай тым оңай емес.
Бұл жердегi негiзгi мәселе жарық жылдамдығымен байланысты
Екi физикалық дерек: бiр жағынан жарық жылдамдығының тұрақтылығы, екiншi жағынан жылдамдықтарды қосудың классикалық заңы бiр- бiрiмен үйлеспейтiндей көрiнетiн. Бiрақ қалыптасқан тығырықтан шығудың жолын алғаш рет 1905 жылы Альберт Эйнштейн тапты. Ол осы қиыншылықтан шығуда өзiнiң ойлап тапқан арнайы салыстырмалылық теориясының негiзiне мынадай екi постулатты алды:
1. Салыстырмалылық принципi: Барлық инерциалды санақ жүйелерi физикалық тұрғыдан тең құқылы. Бастапқы шарт бiрдей болғанда барлық физикалық процесстер мұндай жүйелерде бiрдей болып өтедi. Эйнштейннiң салыстырмалылық принципi деп аталатын бұл принцип Галилейдiң механикадағы салыстырмалылық принципiн барлық, (соның iшiнде электромагниттiк те) процесстер үшiн жалпылайды.
2. Жарық жылдамдығының тұрақтылық принципi: Жарықты көзiнiң, не болмаса жарықты тiркеушiлердiң қозғалғанына, иә қозғалмағанына қарамастан, барлық инерциалды санақ жүйелерiнде, жарықтың жылдамдығы тұрақты шама болып қалады.
Өзара әрекеттесудің таралу жылдамдығы.
Табиғатта өтіп жатқан процестерді сипаттау үшін санақ системасы болу керек. Санақ системасы деп бөлшектердің кеңістіктегі орнын көрсетуге қажет координаттар системасы мен осы системамен байланысқан, уақытты көрсетуге қажет сағатты түсінеді.
Денелердің еркін қозғалысы, яғни сыртқы күштер әсер етпейтін денелердің қозғалысы тұрақты жылдамдықпен өтетін санақ системалары болады. Мұндай санақ системалары инерциалдық санақ системалары деп аталады.
Егер екі санақ системасы бір біріне қатысты бірқалыпты және түзу сызықты қозғалатын болса және олардың біреуі инерциалдық болатын болса, онда оның екіншісінің де инерциалдық болатындығы анық (кезкелген еркін қозғалыс бұл системада да түзу сызықты және бірқалыпты болады) . Сонымен, бір-біріне қатысты бірқалыпты ілгерілемелі қозғалатын кезкелген санды инерциалдық санақ системалары болады екен [10] .
Бір бөлшектен екінші бөлшекке таралатын өзара әрекеттесу жайлы, көбіне, бірінші бөлшектен шығып, екінші бөлшекке бірінші бөлшекте болған өзгерістерді "жеткізетін" сигнал ретінде сөз етеді. Сондай кезде өзара әрекеттесулердің таралу жылдамдығы жайлы "сигналдың жылдамдығы" деп айтады.
Салыстырмалылық принцибінен өзара әрекеттесулердің таралу жылдамдығының барлық инерциалдық санақ системаларында бірдей болатындығы да шығады. Сонымен, өзара әрекеттесулердің таралу жылдамдығы универсал тұрақты болып табылады екен.
Осы тұрақты жылдамдық, сонымен қатар жарықтың бостықта таралу жылдамдығы да болып табылады екен; сондықтан оны жарық жылдамдығы деп атайды. Ол с әрпімен белгіленеді және оның сан мәні
с = 2, 998⋅10 10 см/с (2. 1. 1)
Практика жүзінде көптеген жағдайларда классикалық механиканың жеткілікті дәл болып шығуы міне осы жылдамдықтың шамасының үлкен болуына байланысты түсіндіріледі. Өзіміз істес болатын жылдамдықтардың басым көпшілігі жарық жылдамдығымен салыстырғанда соншалықты аз, сондықтан оны шексіз үлкен деп алу нәтижелердің дәлдігіне еш әсерін тигізбейді.
Өзара әрекеттесулердің таралу жылдамдығының шексіздігінен шығатын Галилейдің салыстырмалылық принципі болса, салыстырмалылық принципін өзара әрекеттесулердің таралу жылдамдығының шектелгендігімен біріктіретін принцип Эйнштейннің салыстырмалылық принципі деп аталады (оны 1905 жылы А. Эйнштейн тұжырымдаған) .
Эйнштейннің салыстырмалылық принципіне негізделген механика релятивистік деп аталады. Қозғалыстағы денелердің жылдамдықтары жарық жылдамдығымен салыстырғанда аз болатын шектік жағдайда өзара әрекеттесулердің таралу жылдамдығының шектелгендігінің қозғалысқа әсерін ескермеуге болады. Сонда релятивистік механика, өзара әрекеттесудің лезде таралатындығы жайлы болжамға сүйенетін байырғы механикаға өтеді; бұл механиканы ньютондық немесе классикалық деп атайды. Релятивистік механикадан классикалық механикаға шектік өтуді формальды түрде релятивистік механика өрнектерінде с → ∞ шегіне өту түрінде атқаруға болады.
Классикалық механиканың өзінде кеңістік салыстырмалы, яғни түрліше оқиғалардың арасындағы кеңістіктік қатынастар олардың қандай санақ системасына қатысты сипатталып отырғандығына тәуелді болады. Түрліше уақыттарда өтетін екі оқиға кеңістіктің бір жерінде немесе жалпы алғанда бір-бірінен белгілі қашықтықта өтеді деген тоқтамның тек оның қай санақ системасына қатысты анықталғандығы көрсетілсе ғана мағынасы болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz