Сандық құрылғылардың математикалық негіздері: логика алгебрасы, логикалық функциялар және типтік комбинациялық құрылғылар


КІРІСПЕ3
1. САНДЫҚ ҚҰРЫЛҒЫЛАРДЫҢ МАТЕМАТИКАЛЫҚ НЕГІЗДЕРІ4
1. 1 Логика алгебрасы4
1. 2 Логикалық функцияларды тапсырма ретінде беру тәсілдері10
1. 3 Қарапайым логикалық функциялар11
1. 4 Логикалық функцияларды таныстыру тәсілдері14
2. ТИПТІ КОМБИНАЦИЯЛЫ ҚҰРЫЛҒЫ20
2. 1 Шифраторлар. Дешифраторлар20
2. 2 Мультиплексорлар, демультиплексорлар және цифрлық компараторлар26
ҚОРЫТЫНДЫ30
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР31
КІРІСПЕБүгінгі таңда күллі әлемде 130 млн-нан аса компьютерлер бар, олардың 80 %-дан артығы әр түрлі ақпараттық-есептеу желілеріне біріктірілген. Мәліметтерді тасымалдаудың компьютерлік желілері болашақта коммуникацияның негізгі құралы болады. Желілерде ақпаратты тасымал-дау жылдамдығы жоғары, жұмыс орнында отырып-ақ хабарлама алу/жөнелту, жер шарының кез келген нүктесінен керекті ақпаратты жылдам алу мүмкіндігі, әр түрлі компьютерлер арасында және әр түрлі программалар арасында мәлімет алмасу, тағы да сол сияқты әрекеттер орындала береді.
Қазіргі заманғы компьютерлердің микроэлектронды схемаларының ақпараттық, арифметикалық және логикалық негіздерін қарастыру адам өмірінде елеулі роль алып отыр. Логикалық және сақтаушы элементтердің, типтік функционалдық түйіндердің, электронды жадының, интерфейстік контроллерлердің құрылу принциптерін меңгеру схемотехника негіздерінің басты қағидаларының бірі болып табылады.
Еліміздегі телекоммуникация саласының тез дамуы жаңа жоғары технологиялық қызметттер - мәліметтерді жіберу, ұялы байланыс және Интернет желісіне қатынауды ұсыну бойынша қызметтер сегментінің туындауымен негізделген. Дәстүрлі дыбыстық байланыс қызметтері интерактивті қызметтермен ығыстырыла бастады. Компьютерлік инфрақұрылымдағы компьютеризация және информатизация жетекші орындардың біріне шығады. Ақпараттық технологияларға сұраныс, қазіргі заманғы компьютерлер және желілік жабдық соңғы жылдары әлемдік экономиканың динамикасына және құрылымына елеулі әсер етеді. Ақпаратты технологиялар саласындағы нағыз төңкеріс үшінші мың жылдықта әлемдік экономиканың жетекші саласына қалыптасқан интернет жүйесінің пайда болуы және қарқынды дамуы болды.
1. САНДЫҚ ҚҰРЫЛҒЫЛАРДЫҢ МАТЕМАТИКАЛЫҚ НЕГІЗДЕРІ 1. 1 Логика алгебрасыСандық құрылғылардың іс әрекетін бейнелейтін математикалық аппарат логика алгебрасында немесе оның басқа атауы ағылшын математигі Джордж Булдің атында бульді алгебра деп атайды.
Математикалық логиканың негізін салған неміс математигі Готфрид Вильгельм Лейбниц (1646 - 1716 жж. ) . Ол универсалды тіл салуға қадам жасаған, соның көмегімен адамдар арасындағы бәсекелесті есеппен шешуге болушы еді. Лейбниц салған негізде ирлан математигі Джордж Буль (1815-1864 жж. ) математикалық логиканың- жаңа ғылым мекемесін салған, ол жай алгебрадан айырмашылығы санмен емес сараптамамен оперирлейді.
Сараптама - бұл қандайда бір тұжырым, соған қатыст немесе жалған, сондай-ақ шындыққа сай ма екенін айтуға болады.
Осымен, сараптама бойынша екілік объект болып табылады, сондықтан сараптаманың шындық мәніне - 1-ге сай, ал жалған мәніне - 0 қояды.
Сараптамалар жай және күрделі болады. Жай сараптамалар алгебраикалық айнымалыларға сай, ал күрделілер алгебраикалық функцияның аналогы болып табылады. Функцияларды айнымалыларды қосу жолымен логикалық іс әрекет көмегімен алуға болады.
Техникалық жүйелерді анализдеу үшінлогика алгебрасын қолдануды көсеткен П. С. Эренфест (1910 ж. ), ал 1938 ж. К. Шеннон Буль алгебрасын релелі сұлбаларын есептеуге қолданған. Осы уақытта логика алгебрасының математикалық аппарат сандық құрылғыларды жобалаудың негізі болып табылады.
Логика алгебрасы екілік айнымалымен оперирлейді, олар шартты белгіленеді, 0 және 1 сияқты. Айнымалыларды белгілеу үшін латын алфавитінің әріптері қолданылады. Алдымызда айнымалыларды белгілеу үшін Х әрпі индексімен, 1ден бастап айнымалының белгіленген нөмірі қолданылады. Функция үшін f (ν) мәні алынған, мұнда ν = (Х n , …, Х 1 ) айнымалылар жиынтығы. Айнымалылар шексіз көп болуы мүмкін, бірақ айнымалы комбинациялар саныжиынтықта үнемі 2 n ге тең
n айнымалыларының функциялары жиын айнымалыларының (Х n , …, Х 1 ) бәріне тәуелді емес, оларды туынды деп атайды. Барлық айнымалылар жиын (Х n , …, Х 1 ) комбинациялары мәні берілген n айнымалыларының функциясытолық анықталған деп аталады. Егер де бір айнымалы жиынының е функция мәні берілмесе, онда ол толық анықталмаған функция болып табылады. Толық анықталмаған функцияны керегінше анықтап, бұл жағдайда оған керек мән беру қажет.
Логика алгебрасының негізінде келесі аксиомалар бар:
Х = 0, если Х ≠ 1
Х = 1, если Х ≠ 0,
аксиома айнымалымен функция тек екі мән қабылдай алатынын анықтайды; _
0 = 1
аксиома терістеу операциясын (инверсия) анықтайды;
0 ∙ 0 = 0
0 ∙ 1 = 0
1 ∙ 0 = 0
1 ∙ 1 = 1,
аксиома коньюнкция операциясын (логикалық көбейту) анықтайды;
0 ∨ 0 = 0
0 ∨ 1 = 1
1 ∨ 0 = 1
1 ∨ 1 = 1,
аксиома дизьюнкция операциясын (логикалық қосу) анықтайды;
Сандық құрылғыны жобалайық, шығысында логикалық 1 болатын, егер үш кiрiс сигналының екеуi бiрлiк мәндi қабылдаса. Ақиқат таблицасында F шығыс функциясы үшiн, үш кiрiс айнымалы А, В және С кiрiс сигналының сегiз мүмкiн болатын терiмi нөлден жетiге дейiн нөмiрленген. (1-сурет)
1 -сурет.
1
2
3
4
5
6
7
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
0
1
0
1
1
1
Әр бiр терiм үшразрядты екiлiк код терiм нөмiрiне сәйкес. Оң жақ бағанада әр бiр терiмге F логикалық функциясының мәндерi көрсетiлген. Ақиқат таблицасы бойынша логикалық функцияға ЖДҚФ (жетiлдiрiлген дизъюнктивтi қалыпты форма) түрiнде теңдiк құруға болады, яғни функцияның бiрлiк терiмiне сай логикалық көбейтiндiлер қосындысы түрiнде:
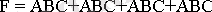 (1)
(1)
(1) Теңдiгi қарапайым логикалық элементтер орындайтын логикалық қосу (дизъюнкция), көбейту (конъюнкция), терiстеу (инверсия) операцияларының көмегiмен жазылған. (2-сурет) .
“Ерекше НЕМЕСЕ” операциясы ЖДҚФ - да мына түрде жазылады
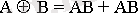 (2)
(2)

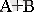
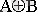
1
2
3
0
1
1
1
0
1
0
0
1
1
1
0
1
1
1
0
0
0
1
1
0

Белгiленуi

ЛИ
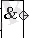
ЛА

ЛЛ

ЛЕ
НЕМЕСЕ
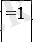
ЛП
2-сурет.
Логикалық функцияны түрлендiру үшiн келесi Буль алгебрасының заңдары қолданылады:
1) Орын ауыстыру А+В=В+А, АВ=ВА;
2) Жиынтықты (А+В) +С=А+(В+С), (АВ) С=А(ВС) ;
3) Тарату А(В+С) =АВ+АС;
4) Екi жақты

5) Екi жақты терiстеу
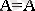
ЖДҚФ-да бұрын жазылған үш айнымалының логикалық функциясы мына түрде берiлуi мүмкiн
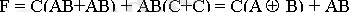 (3)
(3)
(3) теңдiгi бойынша құрылғының функционалдық сұлбасы құрылды (3-сурет) .
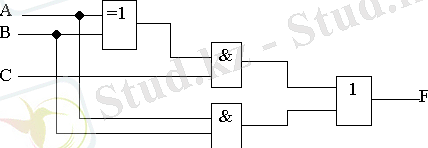
3- сурет.
Логикалық функцияны Венна диаграммасында кескiндеуге болады (4-сурет) . Шеңбердiң iшiндегi аймақ айнымалының тура мәнiне сәйкес, сыртындағы - терiстеуге сәйкес. Венна диаграммасы екi және үш айнымалы бульдiк функцияны минимизациялау үшiн, логикалық теңдiк пен теңсiздiктi дәлелдеу үшiн

4-сурет.
Үш және төрт айнымалы логикалық функцияны минимизациялау үшiн Карно картасын қоолданған ыңғайлы (5-сурет, а және в) . Карно картасы әр бiр тор көздерiнде ақиқат кестесiнiң белгiлi бiр терiмiне сәйкес тiкбұрышты кесте (5-сурет, б және г) . Картада айнымалының тура мәнiнiң аймағы және әр бiр терiмге логикалық функцияның мәнi тiркейдi (0, 1 немесе Х, егер функция берiлген терiмде анықталмаса) .

5 - сурет.
Карно картасы бойынша логикалық функция үшiн минимизацияланған теңдеудiң жазылу ережесi:
1) Бiрлiкпен толтырылған блоктар бөлiнедi;
2) блок тiкбұрышты болу керек және 1, 2, 4, 8 тор көздерiнен тұру керек;
3) блоктар мүмкiндiгiнше үлкен болу керек, ал олардың сандары азболуы керек;
4) Сол және оң, сол сияқты үстiңгi және астыңғы карта жолдары көршiлес болып саналады;
5) Бiр тор көз бiрнеше блокқа кiруi мүмкiн;
6) Кесек блокты алу үшiн, функция кез-келген түрде анықталуы мүмкiн (Х тұрған терiмде) ;
7) Бөлiнiп алынған блокты көрсететiн функция логикалық көбейтiндiлер ЛК түрiнде жазылады;
8) Егер оның нақты мәндерiнiң облыстрының блогы теңбе - тең бөлiнбесе, айнымалы ЛК құрамына кiрмейдi;
9) Егер қарастырылып отырған блок оның инверстiк мән облысында жатса, айнымалы инверсиялы ЛК құрамына кiредi;
10) Блоктағы нөлмен толтырылған тор көздерiн топтау кезiнде, сол ереже бойынша логикалық функцияның инверсиялық мәнiн аламыз.
Карно картасы бойынша (5-сурет, а) V төрт айнымалы логикалық функциясы мына түрде жазылады
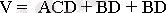
Құрылғыға сай тарату варианты (6-сурет, а) түрлендiрудi ескередi
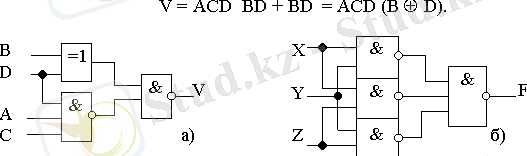
6 -сурет.
Карно картасына сәйкес келетiн (5-сурет, в), үш айнымалы F логикалық функция (оның ақиқат таблицасы 1-суретте бiрдей), жоғарыдағы ереже бойынша мына түрде жазылады:
F = XY + XZ + YZ .
Екi жақтылық формуласын қолданып, ЖӘНЕ -НЕ элементтерiне таратуға ыңғайлы, мына түрге түрлендiруге болады (6-сурет, б) :

Логикалық элементтерде комбинационды сандық құрылғыны жобалау кезiнде, келесi тәртiптi ұсынуға болады:
1) Есеп шарты анықталады (жетiлдiрiлiп отырған құрылғы нақты не iстеу керек екендiгi анықталады, оның жұмыс алгоритмi нақтыланады) ;
2) Берiлген құрылғыға логикалық функция үшiн ақиқат кестесi құрылады;
3) Карно картсының көмегiмен логикалық функцияны минимизациялау жүргiзiледi;
4) Функция берiлген элементтiк базада тарату үшiн ыңғайлы түрге түрленедi;
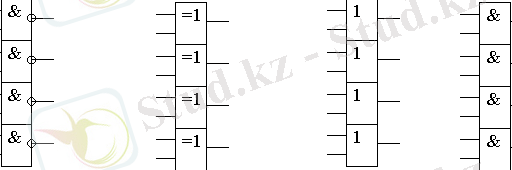
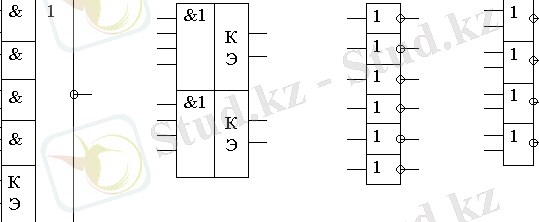
5) Интегралды микросұлбалардың таңдалынған сериялы, логикалық элементтерде сандық құрылғының принципиалды сұлбасы жетiлдiрiледi (7-сурет) .
К155ЛА3
К55ЛА3
КР1533ЛА3
КР531ЛА3
К155ЛП5
К555ЛП5
КР1533ЛП5
КР531ЛП5
К155ЛЛ1
К555ЛЛ1
К531ЛЛ1
К155ЛИ1
К555ЛИ1
КР1533ЛИ1
КР531ЛИ1
Рорт, мВт
tз. орт, нс
I o кiрiс, мА
I 1 кiрiс, мА
I о шығ, мА
I 1 шығ, мА
N
10
20
1, 6
0, 04
16
0, 4
10
2
18
0, 4
0, 02
8
0, 4
20
1, 2
14
0, 2
0, 01
8
0, 4
40
19
5
2
0, 05
20
1
10
7-сурет. ТТЛ және ТТТЛШ логикалық элементтер микросұлбалар мысалдары Рорт. - орташа пайдалану қуаты; tз. орт - таратылудың орташа бөгелуi; I кiрiс және I шығ - кiрiс және шығыс тоқтар токтар; N - жүктемелiк қабiлеттiлiк (қосылатын элементтердiң максималды кiрiс саны) .
Логикалық элемент К155ЛР3, логикалық кеңейткiшке қосылу үшiн К және Э кiрiстерi бар, мысалы, К155ЛД1.
1. 2 Логикалық функцияларды тапсырма ретінде беру тәсілдеріЛогикалық функцияларды әр түрлі тәсілдермен беруге болады: ауызша, ақиқат кестесімен, аналитикалық өрнекпен, шартты графикалық белгілер қолдана отырып. Әрбір нақты жағдайда ең ыңғайлы тәсіл қолданады.
Логикалық функцияны базалық тәсілмен беру ақиқат кестесі болып табылады. Ақиқат кестесінде айнымалы мәндерінің комбинациялары және оларға сай функция мәндері беріледі.
Ақиқат кестесі өзіне жолақ нөмірімен бір қатар қосады (ол міндетті түрде қажет емес, болмауыда болады), қатарлар айнымалылармен (олардың саны айнымалылардың санына тең), қатарлар функциялармен (олардың саны логикалық функциялардың шығысына тең) . Толық ақиқат кестесінің құрамында 2 n жолақтары болады, мұнда n айнымалылар саны. Ақиқат кестесінде жолақтар нөлден бастап нөмірленеді.
Айнымалылар комбинацияларын ақиқат кестесінде қалаған ретте орналастыруға болады, бірақ келесі жүйеге сүйенген жөн. Үлкен айнымалы үлкен индекспен белгіленіп, сол жақ шеткі қатарда орналасады, қалғандары үлкеннен бастап азаю ретімен орналасады. Айнымалы мәндерінің комбинациясы жолақта екілік кодта жол нөмірін өрнектеу керек. Кестеде жолақтар монотонды өсу ретімен орналастырады, нөлден бастап. Мұндай ережелер ақиқат кестесін қатесіз толтырып және онымен жұмыс істеуді жеңілдетеді. Осы ережелермен толтырылған үш айнымалы үшін произволды функцияның ақиқат кестесі 1. 1суретінде көсетілген.
8 - сурет Үш айнымалы үшін ақиқат кестесі
Келтірілген кесте бойынша жай, жылдам қатесіз айнымалылардың мәндерімен толтыру: бірінші қатарда айнымалылар бірден кейін кезектесіп отырады (0-1-0-1 т. с. с. ), екінші қатарда екі реттен кейін (00-11-00 т. с. с. ), үшіншіде төрттен кейін (-- т. с. с. ), төртіншіде сегізден кейін кезектесіп отырады. Келесі үлкен айнымалыға кезектесу дәрежесі екі еселенеді.
Функцияны сөзбен бейнелеуде қандай жағдайда функция 1- ге тең болғанын өрнектеу керек.
1. 3 Қарапайым логикалық функцияларБір немесе екі айнымалылардың функцияларын қарапайым логикалық функциясы деп атайды. Функцияның әр түрлі мәндерінің саны 2 m ге тең, мұнда m 2 n ге тең (n -айнымалылар саны) . Сонымен, бір айнымалы үшін функция саны- 4, ал екі айнымалы үшін - 16. Олардың бәрінде атауы бар және 1 пен 2 кестесінде көрсетілген.
1 кесте - Бір айнымалының функциялары
2 кесте - Екі айнымалының функциялары
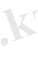 Х
2
Х
1
Х
2
Х
1
Тәжірибеде бір немесе екі айнымалы функцияларының бәрі қолданылмайды. Күрделі сызбаны іске асыру үшін бір екеуі ғана жеткілікті.
Одан басқа, бір функцияларды басқа функция арқылы тепе- теңдік және логика алгебрасының теорема ережелерін қолданып өрнектеуге болады. Интегралды орындауда іске асырылған және микропроцессормен микроконтроллерді бағдарламалау тілінде бар қарапайым функцияларды қарастырайық.
Терістеу ( инверсия, НЕ функциясы) . Айнымалылардың үстіне сызықша белгіленеді. Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 2 суретінде көрсетілген.
9- сурет
Сөзбен бейнелеу: функция инверсті (қарама- қарсы) айнымалы мәнін қабылдайды.
Конъюнкция ( логикалық көбейту, И функциясы) . Айнымалылар арасында ∙ символымен белгіленеді ( сондай да & және ∧ символдары қолданылады ) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 10 суретінде көрсетілген.
f (ν) = Х 2 ∙ Х 1
10- сурет
Сөзбен бейнелеу: функция бірлік мәнді егер барлық айнымалылар бірге тең болса қабылдайды.
Дизъюнкция ( логикалық қосу, ИЛИ функциясы) . Айнымалылар арасында ∨ символымен белгіленеді ( сондай да + символы қолданылады) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 1. 4суретінде көрсетілген.
f (ν) = Х 2 ∨ Х 1
11- сурет
Сөзбен бейнелеу: функция бірлік мәнді бір айнымалы бірге тең болса қабылдайды.
Конъюнкция терістеумен ( логикалық көбейту терістеумен, И- НЕ функциясы Айнымалылар арасында ∙ символымен белгіленеді, өрнек үстіне сызықша қойылады (сондай да & және ∧ символдары қолданылады Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 12 суретінде көрсетілген.
f (ν) = Х 2 ∙ Х 1
12 - сурет
Сөзбен бейнелеу: функция бірлік мәнді, егер бір айнымалы нөлге тең болса қабылдайды.
Дизъюнкция терістеумен (логикалық қосу терістеумен, ИЛИ-НЕ функциясы) . Айнымалылар арасында ∨ символымен белгіленеді, өрнек үстіне сызықша қойылады ( сондай да + символы қолданылады) . Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 13 суретінде көрсетілген.
f (ν) = Х 2 ∨ Х 1
13- сурет
Теңсіздік ( исключающее ИЛИ ) . Айнымалылар арасында ⊕ символымен белгіленеді. Ақиқат кестесі, аналитикалық өрнекпен шартты графиклық бейнелеу 14 суретінде көрсетілген.
f (ν) = Х 2 ⊕ Х 1
14- сурет
Сөзбен бейнелеу: функция бірлік мәнді тек бір айнымалы бірге тең болғанда қабылдайды. Екі айнымалы үшін (бірақ екеуі үшін) осы функция модуль бойынша сомма екі математикалық операциясын көрсетеді.
1. 4 Логикалық функцияларды таныстыру тәсілдеріФункцияның аналитикалық өрнегін ақиқат кестесінен құрауға болады. Осы процессті формальдау үшін кейбір ұғымдарды енгізү керек.
Элементар (қарапайым) конъюнкция ондағы әрбір терістеумен айнымалы немесе терістеусіз бірден көп емес кезігетін болып табылады. Айнымалылар тобының терістеуі болмайды.
Мысалы:
Элементар (қарапайым) дизъюнкция ондағы әрбір терістеумен айнымалы немесе терістеусіз бірден көп емес кезігетін болып табылады. Айнымалылар тобының терістеуі болмайды.
Мысалы:
Минтерм (бірліктің конституенттісі) дегеніміз осы жағдайда барлық қолданылатын айнымалыларды қамтитын элементар конъюнкция.
Мысалы, егер үш айнымалы қолданса, онда конъюнкция минтерм болып табылады
бірақ конъюнкциялар
минтермдер болып табылмайды.
Минтерм 1-ге тең тек айнымалылардың бір комбинациялары үшін.
Минтерм К i символымен белгіленеді, мұндағы i - индекс, ол бірмәнде минтермнің (конъюнкциямен) аналитикалық өрнегімен тепе- тең болады. Минтерм индексін біле отырып, оның аналитикалық өрнегін анықтауға немесе керісінше болады.
Егер минтерм индексі берілсе, онда ол екілік кодта жазылады. Сонан соң әрбір разрядында 1 инверсиясыз айнымалымен, ал 0 инверсиясы бар айнымалылармен ауыстырылады. Ауыстырғанда айнымалылардың үлкендігі екілік код разрядтарының үлкендігіне (позицияларға) сай болуы керек.
Мысалы, үш айнымалы үшін К 6 минтермінің аналитикалық өренгін алуымыз қажет. Айнымалыларда Х 3 , Х 2 , Х 1 мәндері бар. . Нөмірі неғұрлым көп болса, соғұрлым айнымалы да үлкен болады.
Берілген минтерм индексі - 6. 6 санының екілік кодтағы түрі 110. Үлкен разряд солжақтағы біріншісі. Минтерм аналитикалық өренгінде Х 3 және Х 2 айнымалылар инверсиясыз болады, ал Х 1 айнымалысы инверсиямен болады.
Минтерм аналитикалық өрнекті анықтау үшін келесі алгоритмді қолдануға болады. Айнымалылар үлкендік ретімен жазылады, ал олардың астына 6 санының екілі коды үлкен позициясын сақтаумен жазылады:
Х 3 Х 2 Х 1
1 1 0
Астында 0 тұрған айнымалылар инверсиясы бар минтермнің аналитикалық өрнегіне кіреді. Сонымен минтерм аналитикалық өрнегі 6 индексімен үш айнымалы үшін:
К 6 =
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz