Комбинациялық микросхемалар: қосындылағыштар мен санағыштардың теориясы мен құрылымы


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:
КІРІСПЕ3
1. КОМБИНАЦИЯЛЫҚ МИКРОСХЕМАЛАРДЫҢ ҚОЛДАНЫЛУЫ4
1. 1 Қосындылағыш4
1. 2 Екілік қосындылағыштардың қолдануы9
2. САНАҒЫШТАР14
2. 1 Жалпы түсініктеме14
2. 2 Санағыштарды құру сызбасы17
2. 3 Есептеу модулі ерікті санауыштар25
ҚОРЫТЫНДЫ26
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР27
Қазіргі заманғы компьютерлердің микроэлектронды схемаларының ақпараттық, арифметикалық және логикалық негіздерін қарастыру адам өмірінде елеулі роль алып отыр. Логикалық және сақтаушы элементтердің, типтік функционалдық түйіндердің, электронды жадының, интерфейстік контроллерлердің құрылу принциптерін меңгеру схемотехника негіздерінің басты қағидаларының бірі болып табылады.
Еліміздегі телекоммуникация саласының тез дамуы жаңа жоғары технологиялық қызметттер - мәліметтерді жіберу, ұялы байланыс және Интернет желісіне қатынауды ұсыну бойынша қызметтер сегментінің туындауымен негізделген. Дәстүрлі дыбыстық байланыс қызметтері интерактивті қызметтермен ығыстырыла бастады. Компьютерлік инфрақұрылымдағы компьютеризация және информатизация жетекші орындардың біріне шығады. Ақпараттық технологияларға сұраныс, қазіргі заманғы компьютерлер және желілік жабдық соңғы жылдары әлемдік экономиканың динамикасына және құрылымына елеулі әсер етеді. Ақпаратты технологиялар саласындағы нағыз төңкеріс үшінші мың жылдықта әлемдік экономиканың жетекші саласына қалыптасқан интернет жүйесінің пайда болуы және қарқынды дамуы болды.
Бұл курстық жобада жалпы сумматорлар жайында және санауыштардың орындалуы және қызметі қарастырылады.
Сумматор деп - екілік код түрінде берілген, сандардың арифметикалық операцияларын орындауға арналған комбинациялық-логикалық құрылғы.
Сумматорлар арифметика-логикалық құрылғыларының негізгі торабы болып табылады. Сумматор термині кең көлемді құрылғыларды қамтиды, қарапайым логикалық схемалардан бастап, күрделі цифрлық түйіндерге дейін. Осы барлық құрылғыларға ортақ болып табылатыны - берілген сандардың арифметикалық қосындысы
Қосындылағыш - ЭЕМ-нің функционалды түйініғ үш екілік санды қосуға (қосылатын сандар және алдыңғы разрядтан тасымал) және шығысында қосынды сигналы мен тасымалдарды қалыптастыру үшін арналған.
Жіктелуі :
1. Кірістер саны бойынша:
- жартылайқосындылағыш;
- бірразрядты қосындылағыш;
- Көпразрядты қосындылағыштар:
* тізбекті;
* параллельді;
2. Разрядаралық тасымалдарды ұйымдастыру тәсілі бойынша:
- тізбекті тасымалды;
- параллель тасымалды;
- топтық құрылымды;
3. Логикалық құрылымы бойынша:
- комбинационды қосындылағыштар;
- жинақтаушы қосындылағыштар;
4. Тактілеу тәсілі бойынша:
- асинхронды;
- синхронды;
5. Санау жүйесіне байланысты:
- екілік;
- Екілік-ондық;
- басқа да.
Базалық сұлбасы :
1. Бірразрядты екілік комбинациондық қосындылағыш:
Жылдамдығы жоғары , дегенмен S i және P i сигналдары тек кіріс сигналдарының әсері кезінде ғана жұмыс істейді (сақтау жоқ) .
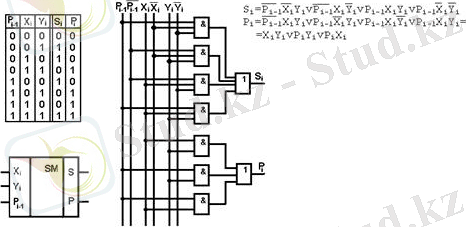
1 - сурет. Бірразрядты екілік комбинациялық қосындылағыш
2. Бір разрядты жинақтауышты екілік қосындылағыш:
Жұп санауыш триггерлер негізінде құрылады. Комбинациялықпен салыстырғанда жылдамдығы төмен (кіріс сигналдары тізбектей келіп түседі) .
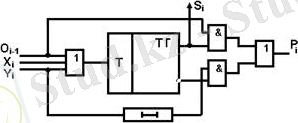
2 - сурет. Бірразрядты жинақтаушы екілік қосындылағыш
3. Көп разрядты тізбекті қосындылағыш:
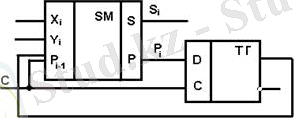
3 - сурет. Көпразрядты тізбекті қосындылағыш
4. Тізбекті тасымалды көпразрядты параллель қосындылағыш:
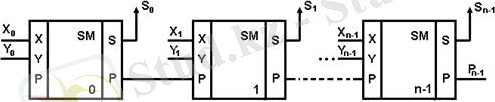
4 - сурет. Тізбекті тасымалды көпразрядты параллель қосындылағы
Қосындылағыштар сандардың арифметикалық (логикалыққа қарсы) қосу мен алуын орындайды. Олардың өз дербес мағынасы бар және олар әртүрлі операциялар қатарын жүзеге асыратын және барлық процессорлардың өте қажет бөлігі болып келетін арифметикалық логикалық құрылғының (АЛҚ) сұлбасының ядросы болып табылады.
Жартылай қосындылағыш (HS) екі қос сандардың кіші разрядтарының биттарын қосуға қызмет етеді. Ақиқат кестесі бойынша жүзеге асыруға болады. S-қосынды сан, Р - келесі разрядқа тасымалдайтын шығу.
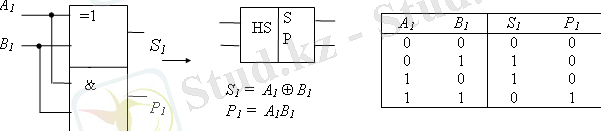
5 - сурет. Жартылай қосындылағыш
Толық бірразрядты қосындылағыш екі екілік санның сәйкес разрядтарының биттарын қосады, алдындағы разрядтан тасымалды есепке алып, келесі разрядқа тасымалды өңдіреді. Оны екі HS жартылай қосындылағыш мен НЕМЕСЕ логикалық элементтен құрастыруға болады. Толық бірразрядтты қосындылағыш 4. 17 суретінде көрсетілген.
Қосындылағыш үлгісі ретінде ИМС К555ИМ5 (4. 18 сурет) көрсетілген, оған екі толық бірразрядтты қосындылағыштар кіреді. Ол кіші разрядтан аға(бас) разрядқа тасымалдауды есепке ала отыра, екілік кодтағы үш бірразрядты сандардың қосу операциясын орындайды.
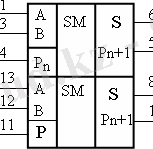
7 - сурет. ИМС К555ИМ5
Сандық (цифрлік) техникада қосындылағыштар (соммалаушы) көмегімен барлық арифметикалық операциялар орындалады. Берілген жұмыста төртразрядты қосындылағыш микросызбасын зерттеу және іске қосылуы орындалады. Қосындылағышдың қызметін сипаттау үшін ең алдымен, қарапайым сандық сызба техникасының элементтерін, яғни, жартылай соммалаушыларды қарастыру болып табылады.
Жартылай соммалаушы - бұл екі бір разрядты екілік сандарды соммалаушы орындайтын ЭЕМ түйіні. Бұл сандар екі көпразрядты екілік кқдтардың разрядтары болып табылады. Соммалау екілік арифметика ережелері бойынша орындалады:
0+0=0; (1)
0+1=1; (2)
1+0=1; (3)
1+1=10. (4)
Егер екі санды қосқан кезде, оның біреуі нөлге тең болса онда нәтиже бірразрядты (алғашқы үш есептеу) екені есептеуде көрсетілген. егер екі сан бірге тең болса (төртінші есептеу), онда нәтижесінде екінші разряд шығады. Бұл разряд екі келесі сомасы үшін аудару белгісі болып табылады, яғни көпразрядты екілік сандардың қосындысының үлкен разрядтары болып табылады.
Бірразрядты комбинациялық соммалаушы - бұл күрделі комбинациялық сызба болып табылады. Бұл сызбада үш бірразрядты сандарды соммалау іске асырылады. екі бірразрядты сандардың қосындысынан басқа, сомада алдыңғы разряд соммаларының аудару белгісі қатысыды. Екілік сандардың арифметикалық ережелеріне сәйкес және соммалаушы үшін нақтылық кестесін құруға болады. (Кесте 2) .
2 Кесте. Соммалаушы үшін қосындылағыша
Кестедегі алынған есептеулер келесі түрде болады:
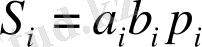 +
+
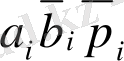 +
+
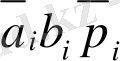 +
+
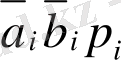 ;
;
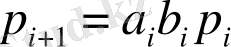 +
+
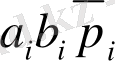 +
+
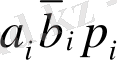 +
+
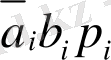 ;
;
Сонымен қатар, осы есептеулер бойынша комбинациялық соммалаушының қызметтік сызбасын құрастыруға болады, логикалық элементтерге сәйкес қолдану арқылы. Есептеулер қысқармайтындықтан, оны S i және p i+1 формуласында ұқсас мүшелер, мүмкіндігінше, болсын деп мақсаткерлі өрнектеген, ол қолданатын элементтердің санын қысқартады. Өрнектеудің бір нұсқасы мына есептеуді береді:
S=ABP+(A+B+P) *P
P = AB+AP+BP
2 суретте қызметтік сызба көрсетілген, осы есептеулерді және талапты графикалық соммалаушының белгіленуін іске асырады.
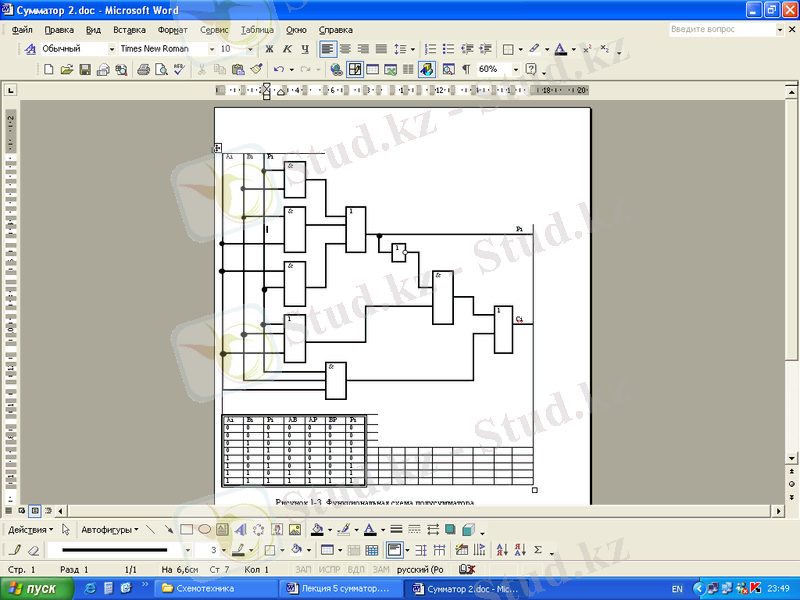
Сандық сызба техникасында тетрадтарды қосу есебі бар, яғни төртразрядты екілік кодтарды өзара қосу. Мұндай операцияны көпразрядты комбинациялық қосындылағыш орындайды. Бұл сызбалар бірразрядты комбинациялық қосындылағыштар негізінде құрылған, яғни оларды каскадты қосу жолымен құрған. Олар біртізбекті және параллелді болуы мүмкін.
Олардың сомасын біртізбекті кодқа екі ондық тетрадтарды тізбектей қайта түрлендіру және оларды ондық тетрад түрінде ұсыну, қосындылағыштардың каскадты қосуын қолданудан қарағанда өте күрделі болып табылады. Бірразрядты комбинациялық қосындылағыштардың каскадтық қосылуы параллелді қосындылағыш түрінде келеді. Бұл қосындылағыштар тізбектей, параллель және топтық ауыстырулар болып келеді. Қосындылағыштарды ауыстыру әдістері ең алдымен микросызбалардың жылдам әрекет етуін анықтайды.
Қосындылағыштардың жұмыс істеу логикасын қарастыруда жылдам әрекет ету берілген міндетпен анықталмаған, сондықтан бірразрядты комбинациялық қосындылағыштардың қарапайым қосылу сұлбасы ұсынылған (3 сурет) . Бұл сұлбада қосылушы сандарды, алдыңғы тетрадтар соммасының ауыстыру белгісі және келесі тетрадтар соммасының ауыстыру белгісі кіші әріптермен көрсетілген. Үлкен әріптермен белгілер локальді көрсетілген, яғни әр бірразрядты қосындылағыш үшін.
Бұл сұлбада тізбектелген ауыстыру орындалған. Екі көпразрядты екілік сандарды қосу ең кіші разрядтан басталады және разрядтар бойынша төрт тактылы осы сұлба бойынша тізбектей орындалады. ы.
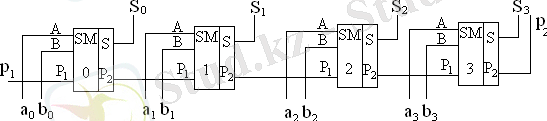
9 - сурет. Тізбектелген ауыстырумен параллельді комбинациялық қосындылағыш
1. 2 Екілік қосындылағыштардың қолдануы
Екілік қосындылағыш(сур. 10, а) А және В n-разрядты екілік сандарының арифметикалық суммасын түзу үшін қызмет етеді (сур. 10, б) .
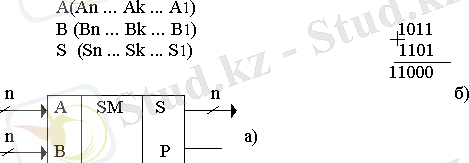
10 -сурет
Қосу нәтижесі болып қосындының бесінші разряды деп қарастыруға болатын S төртразрядты қосындысы және Р ауысу болып табылады. Кіші разрядты биттерді өңдеу кезінде жарты қосындылағыштар қолданылады.
Жартылай қосындылағыштарды ЖӘНЕ және “Ерекше НЕМЕСЕ” логикалық элементтерінде жүзеге асыруға болады (сур. 11) .
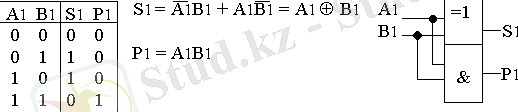
11 - сурет

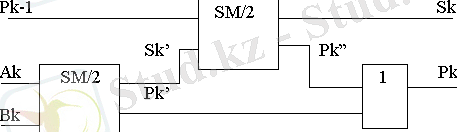
12 - сурет.
Екі жартылай қосындылағышдан және НЕМЕСЕ логикалық элементінен толық бірразрядты қосындылағыш құруға болады (сур. 12) .
К155ИМ3 микросұлбасының корпусында төрт толық бірразрядты қосындылағыш, төртразрядты қосындылағыш сұлбасына біріктірілген (сур. 12) .
Микросұлбаның қосымша полесінде қосындылағышдың кіріс және шығысының салмақтық коэфициенттері көрсетілген.
Ұяшықтар қоймасында сандық индикаторда санның (0-ден 9-ға дейін) детальдарын көрсететін құрылғыны жобалайық.
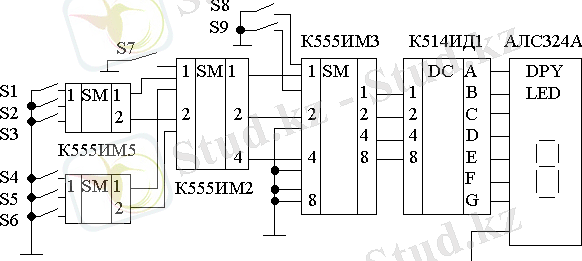
13 -сурет.
Есеп қосындылағыш көмегімен жеңіл шешіледі (сур. 13) . Бір разрядты (К555ИМ5), екіразрядты (К555ИМ2) және төрт разрядты (К555ИМ3) қосындылағыштар микросұлбалары іске қосылған, S1-S9 ажыратып қосқышының тең салмақпен тоғыз сигналын қосындылау керек. К514ИД1 дешифраторы арқылы қосынды сан жерлендірілген АЛС324А сандық жарықдиодты индикаторына беріледі .
Кәдімгі қосындылағыш қосымша код белгісімен берілген сандарды қосу үшін қолданылады. Шығысында қосымша қосынды коды пайда болады. Осылай сегізразрядты қосындылағыш көмегімен байттық қосындылардың алгебралық қосындысын жүргізуге болады. Бірдей белгісі бар санды қосу кезінде, модуль қосындысы 127 ден аспауы керек.
Қосындылағышдың кірісіне +100 және -16 сандарының қосымша кодтары берілсін. Шығысында аламыз

Сандардың n-разрядты екілік және екілік-ондық кодын салыстыру нәтижесін тіркейтін құрылғы сандық компаратор деп аталады (сур. 14) . А> белгісімен шығысында логикалық бірлік түзіледі, егер А>B және A=<B кезінде логикалық 0. A< белгісімен шығысында логикалық бірлік түзіледі, егер A<B және A>=B кезінде логикалық 0. А= шығысында логикалық бірлік, кодтар сәйкес болғанда түзіледі.
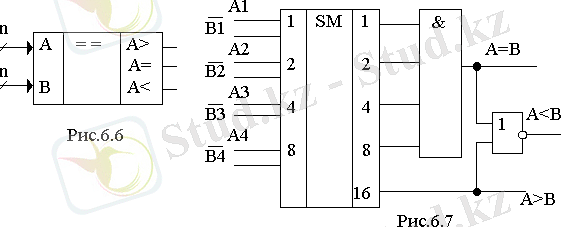
14-сурет,
Сандық компараторды қосындылағышда салуға болады, бір кірісінде А түзу сан кодын береді, келесі В инверсті сан коды (сур. 14) . Сандық мысалдарда, А=В үшін кіші төрт разрядты логикалық бірге тең, ал A>B үшін ауысу шығысында бірге ауысады.
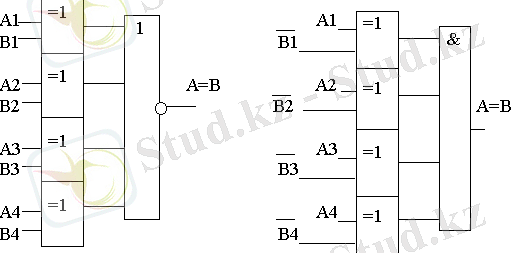
15- сурет
Тең белгілі код сұлбасын логикалық элементтерде құруға болады (сур. 15) . Интегралды микросұлбалардың кейбір сұлбаларында сандық компараторлар болады (мысалға, К555СП1) .
Логикалық схемаларда қолданылатын екілік сандарды қосу, көбейту амалдары жиі қарастырылады. Екілік санды қосу тасымалдау есебімен сәйкес разрядтарды қосуға әкеледі.
Екі екілік санды қосуды жүзеге асыратын логикалық элементтердің шартты графикалық бейнеленуімен шындық кестесін (3. 8-кесте) қарастыралық.
2-кесте. Жартылай қосындылағыш шындық кестесі
мұндағы, А, В - кіріс сигналдары, Σ - қосынды, С0 - шығыс тасымал дегенді білдіреді.
Бұл кестеден С 0 =А*В екенін көреміз. Мұндай талап етілетін логикалық деңгейді алу үшін ЖӘНЕ элементін пайдалануға болады. Ал, енді қосынды шығысындағы күйді бульдік өрнекпен сипаттауға тырысалық. Сонда Σ=А*В+В*А бұл өрнек үшін 2 ЖӘНЕ-ЕМЕС 1 НЕМЕСЕ логикалық элементтері пайдаланылады, яғни, шектеулі НЕМЕСЕ пайдаланылады. Σ=АВ.
Сонымен, шектеулі НЕМЕСЕ салыстыру схемасы ғана емес, оның басқа маңыздылығы да бар. Ол оның шындық кестесін екілік сандарды қосу кестесімен салыстырудан шығады. Мұнда тек жоғары разрядқа көшу қарастырылмайды, оны қалыптастыру үшін салыстыру схемасына (шектеулі немесе) сәйкестендіру схемасын (және) қосу керек. Соңғысы А және В аргументтерінің екеуінің де мәндері бір мезгілде 1 болғанда ғана логикалық бірлікті туғызады. Шыққан схема жартылай қосындылағыш деп аталады.
Толық қосындылағыш үш кіріске ие. Көп разрядты екілік сандарды қосу үшін бірнеше жартылай және толық қосындылағыштар қажет. Мысалы, үш разрядты параллель қосындылағыш. Мысал ретінде тізбектелген әрекеттер қосындылағышын қарастырамыз.
16-сурет. Қосындылағыш
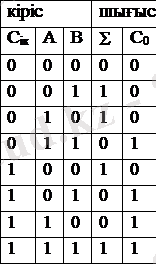
Мұның барлық мүмкін екілік разрядты А, В, С ік (cаrry input) қосылғыштары комбинациясы үшін шындық кестесі:
3-кесте. Қосындылағыш шындық кестесі
Санағыш дегеніміз - бұл функционалды тізбектес құрылғы. Оның шығысындағы сигналдар комбинациясы С санау кірісіне импульстің активті ауысуы келіп түскенде белгілі бір заңдылықпен өзгереді. Шығыс сигналдарының өзгеру заңдылығы санағыштың ішкі күйін кодтаудың таңдалған әдісімен анықталады. Басқалардан қарағанда екілік, екілік-ондық, унитарлы кодтар жиі қолданылады. Осы кодтарды қолданатын санағыштар интегралды орындауда шығарылады және, сәйкесінше, екілік, екілік-ондық, сақиналық деп аталады. Санау кірісінен басқа санағышта оның мүмкіндіктерін кеңейтетін басқа да кірістері болуы мүмкін (бастапқы күйге құру, жұмысты шешу және т. б. ) .
Конструкторлық документацияның бірыңғай жүйесі (ЕСКД) С санау кірісін белгілеудің (және жалпы динамикалық ИМС кірістерін) бірнеше нұсқаларын ұсынады. Бұл нұсқалар 17-суретте көрсетілген : а) 0-ден 1-ге ауысу бойынша басқару (оң ауысу бойынша, фронт бойынша), және 17 б) суретінде- 1-ден 0-ге ауысу бойынша басқару теріс ауысу бойынша (қайту (спад) бойынша ) . Форма 1 суреті ең қолайлы болып табылады.
Санағыштың бастапқы күйін және пайдаланатын кодты біле тұра, шығыс сигналдарының комбинациясы бойынша оның санау кірісіне дәл сол мезетте келіп түскен импульстердің санын анықтауға болады. Сондықтан санағыштарды импульстерді санау үшін де қолдануға болады.
Санағыштың тұрақты күйінің (шығыстағы сигналдар комбинациясы) саны санаудың модулі немесе коэффициенті деп аталады. Санау модулі М деп белгіленеді және ол М модулі бойынша санағыш деп аталады. Санағышпен есептелуі мүмкін импульстердің максимал саны ( санағыш сыйымдылығы ) М-1 - ге тең. Санау кірісіне кезекті М-1 - ден кейінгі импульстің активті ауысуы келіп түскенде, санағыш бастапқы күйге ауысады. Мұндай жағдай санағыштың толып кетуі деп аталады.
Санағыштың модулі қолданатын кодқа және санағыш шығысының санына байланысты. Шығыс саны «n» болғанда, санаудың максимал модулі екілік үшін « 2 n », ал сақиналық санағыш үшін «n» (шығыс саны разряд санына тең) тең. Екілік-ондық санағышта бір ондық разряд үшін төрт шығыс (декадалар) қажет және мұндай декадалардың максимал санау модулі - 10.
Егер санағыштың кірісіне f жиілікті импульстар тізімі берілсе, санағыштың толып кетуіне периодты түрде f/M жиілігімен пайда болады. Бұл қасиет жиілікті бөлу үшін қолданылады. Мұндай жағдайда шығыс сигналы соңғы разрядтан немесе толып кетуден қалыптасатын импульсі бар арнайы шығыстан түсіндіріледі. Сондықтан тек қана жиілікті бөлу үшін арналған санағыштарда бір негізгі шығысы болады және олар санағыш-бөлгіштер немесе сандық таймерлер деп аталады.
Қалпының өзгеру тәртібіне байланысты санағыштар қосып жинақтау (өспелі тәртіпте) және азайту (кемімелі тәртіпте) болады. Мысалы, қосып жинақтайтын екілік санағышта импульстің санау кірісіндегі әрбір активті ауысу осы санағышта жазылған санға бірді қосады, ал азайтатында бірге азайтады. Егер санағыш екі режимде де жұмыс істей алатын болса, онда ол реверсивті деп аталады. Интегралдық орындауда қосып жинақтайтын және реверсивті санағыштар шығарылады. Олардың қосып жинақтау режиміндегі бастапқы комбинациясы нөлдік, азайту режимінде М-1 .
Санағыштар триггерлерден құралады және түрлілігіне байланысты синхронды және асинхронды болып бөлінеді. Құрылымы бойынша асинхронды санағыштар тізбектес неесе параллель ауысуымен болуы мүмкін. Синхрондық санағыштар ең күрделі және жылдам әсер еткіш.
Жылдам әсер еткіштігі маңызды параметр болып табылады. жұмыс кезінде әлі жаңылу болмайтын екі активті ауысу арасындағы минималды уақытпен және активті ауысу пайда болып, жаңа күйдің (құру уақыты) құрау арасындағы уақытпен анықталады. Санаудың максималды жиілігі анықталады.
Көптеген санағыштардың бастапқы күйін қалауымызша өзгертуге болады. Бұл үшін оларда бастапқы күйді құрудың арнайы кірісі бар. Осы кіріске керекті бастапқы күйге сәйкес код комбинациясы және загрузканы басқару кірісі жіберіледі.
Асинхронды загрузкеасы бар санағыштарда ақпарат бастапқы күйді құру кірісінен загрузканы басқару кірісінде сигналдың активті деңгейі пайда бола салысымен-ақ шығысына көшіріледі.
Айтарлықтай барлық санағыштарда нөлдік күйге түсіру кірісі бар. Ол басқа кірістерге қарағанда басты басымдылыққа ие.
Санағыштар, өздік элементтер сияқты, әр түрлі сигналдардың санын есептеуге, жиілікті азайтуға, сондай-ақ түрлі құрылғыларды (сандық фазаайналдырғыштар, жиілік синтезаторы, т. б. ) құру кезінде қолданылады. Қазіргі уақытта интегралдық орындауда шығарылатын санағыштар: тікелей байланысы бар асинхронды, параллелдік ауысуы бар асинхронды және синхронды.
Санағыш - ЭЕМ функционалды түйіні, кірісіне келіп түскен сигналдар санын санауға және оны n-разрядты екілік код түрінде беруге арналған.
Санағыш санайтын максимальды сан N=2 n санау коэффициентін түзеді, мұндағы N - санағыш разрядтылы. Санағыштар біртактылы екісатылы Т-триггерлерінде құрылады.
Жіктелуі :
1. санау бағыты бойынша
- қосындылаушы;
- азайтушы;
- реверсивті;
2. санау жүйесі бойынша :
- екілік;
- екілік емес:
* екілік-ондық;
* еркін коэффициентті;
3. сигналдардың келіп түсу уақыты бойынша :
- асинхронды;
- синхронды;
4. разрядты тасымалды ұйымдастыру тәсілі бойынша :
- тізбекті тасымалды;
- параллель тасымалды;
- аралас тасымалды (топтап) ;
Базалық сұлбасы:
1. Тізбекті тасымалды қосындылаушы асинхронды екілік санағыш.
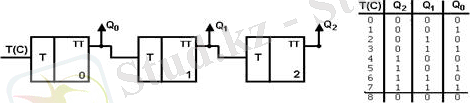
18 - сурет. Тізбекті тасымалды қосындылаушы асинхронды екілік санағыш
2. Параллель тасымалды қосындылаушы синхронды екілік санағыш.
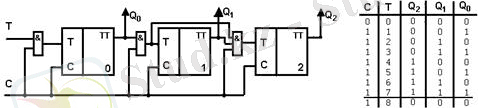
19 - сурет. Параллель тасымалды қосындылаушы синхронды екілік санағыш
Ауыстырып қосу (кіріс сигналдарын санау) тек С синхросигналы бар болғанда ғана мүмкін болмақ.
3. Параллель тасымалды азайтушы синхронды екілік санағыш.
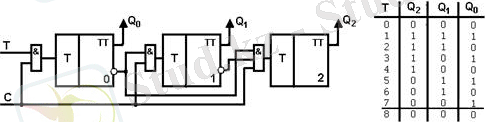
20 - сурет. Параллель тасымалды азайтушы синхронды екілік санағыш
4. Параллель тасымалды қосындылаушы синхронды ондық санағыш
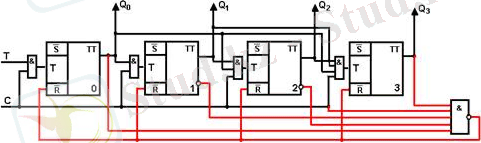
21 - сурет. Параллель тасымалды қосындылаушы синхронды ондық санағыш.
2. 2 Санағыштарды құру сызбасы
Құрылымы бойынша ең қарапайым асинхронды екілік санағыштар болып табылады. Ол 22-суретінде көрсетілгендей, бір-біріне тізбектей жалғанған асинхронды Т-триггерлерден тұрады.
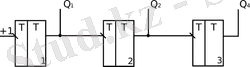 Бір триггердің шығысы екінші триггердің кірісіне жалғанған бұл сызба тікелей байланысы бар сызба деп аталады. Екілік санағыштарда қолданбалы триггерлердің саны разряд санына тең болады.
Бір триггердің шығысы екінші триггердің кірісіне жалғанған бұл сызба тікелей байланысы бар сызба деп аталады. Екілік санағыштарда қолданбалы триггерлердің саны разряд санына тең болады.
22-сурет. Тікелей байланысы бар санағыш.
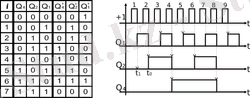 Санағыштың жұмысын уақыттық диаграммамен түсіндірген ыңғайлы. Қарастырылып отырған санағыш үшін мұндай диаграмма 23 -суретте келтірілген. Санағыштың бастапқы күйі нөлдік. Бірінші триггердің
Санағыштың жұмысын уақыттық диаграммамен түсіндірген ыңғайлы. Қарастырылып отырған санағыш үшін мұндай диаграмма 23 -суретте келтірілген. Санағыштың бастапқы күйі нөлдік. Бірінші триггердің
23 - сурет
кірісінде 1-ден 0-ге ауысу пайда болғанда ол нөлден бірге аусысады (t 1 ) . Бірінші триггердің кірісінде екінші 1-ден 0-ге ауысу пайда болғанда ол
бірден нөлге ауысады, ол екінші триггердің кірісінде 1-ден 0-ге ауысуды тудырады, ол нөлден бірге ауысады (t 2 ) . Үшінші 1-ден 0-ге ауысу пайда болғанан кейін бірінші триггер қайтадан ауысады және т. с. с. Диаграммадан байқайтынымыздай, сегізінші импульстан кейін толып кету жүреді де, санағыш қайтадан алдыңғы қалпына құрылады.
Санағыштың кезектес жұмысын сондай-ақ күй кестесінен де (ауысу функциялары) көруге болады. Қарастырылып отырған сызба үшін бұл кесте 23 -суретте келтірілген. Бірінші бағанда күйдің нөмірі көрсетілген, екіншіде шығыстың импульстің активті ауысуы келіп түскенге дейінгі мәні, үшіншіде - келіп түскеннен кейінгі мәні келтірілген.
Сызбада 22-суретте триггерлер бірінші триггердің кірісіндегі активті ауысуға қатысты t=n*t 3 уақыт ішінде тізбектей ауысады. Мұндағы n - триггерлер саны, t 3 - бір триггердің қайта қосылу уақыты. Бұндай сандардың жылдам әсер етуі разрядтар санына тәуелді және олардың саны ұлғайса, жылдам әсер еткіштігі төмендейді.
Бұл кемшілікке қарамастан, өзінің қарапайымдылығының және жеңіл өсімшілдігінің арқасында мұндай санағыштар кеңінен қолданыста жүреді.
Тікелей байланысты К1533 екілік санағыштың ШГБ-уі және оның құрылым сызбасы 24-суретте келтірілген. Санағышта екі С0 мен С1 санау кірісі бар және екі құру R 1 , R 2 кірісі бар. Триггерлерден құрылған (DD2-DD4) құрылған тізбек сегізге санағыш-бөлгішті құрайды, DD1 триггері жекеленген екіге бөлгіш сияқты жұмыс істейді. Егерр барлық триггерлерді тізбектей қосатын болсақ, Q 0 шығысы С1 кірісіне қосылғанда, санау модулі 16 болатын санағыш пайда болады.
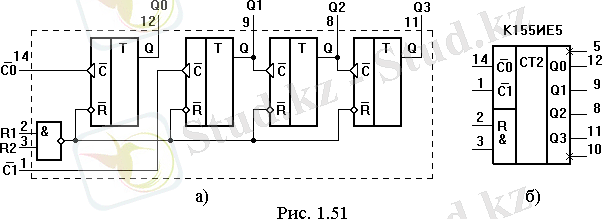
24 - сурет а) ШГБ және б) К1533ИЕ5 санауыштың структуралық сызбасы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz