7-8-9 сыныптардан геометриядан таңдау курстарын оқыту

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 97 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . 3

НЕГІЗГІ БӨЛІМ

1 . Бейіндік оқыту . . . 5

2. Қарапайым геометриялық фигуралардың негізгі қасиеттері (7-8 сынып оқу бағдарламасы негізінде)

2. 1. Геометрия. Геометрияның шығу тарихы . . . 8

2. 2. Қазақстанда геометрия ғылымының зерттеу жұмыстар. Геометрияның түрлері. Геомертия философияда және өнерде. ……13

2. 4. Нүкте. Түзу. Бұрыш. . 15

2. 5. Үшбұрыш. Төртбұрыш . . . 18

3. Төртбұрыштарды оқыту әдістемесі мен классификациясы(8-сынып оқу бағдарламасы негізінде)

3. 1 Классификация және әдістемелік нұсқаулар . . . 22

3. 2 Параллелограмм қасиеттерін қолданып есептерді шешу

әдістемесі . . . 26

3. 3 Тікбұрыш, ромб, квадрат қасиеттерін қолданып есептерді шешу

әдістемесі . . . 28

3. 4 Фалес теоремасы . . . 31

3. 5 Трапеция және оның қасиеттері . . . 33

3. 6 Үшбұрыш және трапеция орта сызықтары . . . 36

3. 7 Үшбұрыштың тамаша нүктелері . . . 39

4. Тікбұрышты үшбұрыштарды оқыту әдістемесі(8-9 сынып оқу бағдарламасы негізінде)

4. 1 Тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының

арасындағы байланыстар . . . 43

4. 2 Тікбұрышты үшбұрыштың (сүйір бұрышының) синусы,

косинусы, тангенсі және котангенсі . . . 44

4. 3 Пифагор теоремасы . . . 46

4. 4 Негізгі тригонометриялық тепе-теңдіктер әдістемесі . . . 48

4. 5 Жиі кездесетін бұрыштар үшін синустың, косинустың, тангенстің

және котангенсінің мәндері . . . 49

4. 6 Тікбұрышты үшбұрыштарды шешу әдістемесі . . . 51

4. 7 Есеп шығару үлгілері . . . 53

5. Тікбұрышты координаталар жүйесі және оның қысқаша

тарихы мен әдістемесі (9-сынып оқу бағдарламасы негізінде

5. 1 Геометриядағы координаталық әдіс . . . 56

5. 2 Жазықтықтағы нүктелердің және кесіндінің орта нүктесінің

координаталары . . . 58

5. 3 Екі нүктенің арақашықтығы . . . 60

5. 4 Шеңбердің теңдеуі . . . 62

5. 5 Түзудің теңдеуі . . . 67

5. 6. Есептерді шығару үлгілері . . . 72

6. Төртбұрыш ауданы және оны оқыту әдістемесі(9-сынып оқу бағдарламасы негізінде)

6. 1 Негізгі түсініктер . . . 74

6. 2 Фигураның ауданы туралы оқыту әдістемесі . . . 80

6. 2. 1 Тік төртбұрыштың ауданы . . . 80

6. 2. 2 Параллелограмм ауданы . . . 81

6. 2. 3 Үшбұрыш ауданы . . . 82

6. 2. 4 Трапеция ауданы . . . 83

6. 3 Есептерді шығару үлгілері . . . 84

Қосымша . . . 89

Қорытынды . . . 94

Пайдаланған әдебиеттер . . . 96

КІРІСПЕ

Дипломдық жұмыстың тақырыбын «7-8-9 сыныптардан геометриядан таңдау курстарын оқыту» деп таңдап алдым, өйткені:

1. Алғашқы геометриялық мағлұматтар 1-4 сыныптарда алынады, демек арада аз ғана жыл өтіп ол мағлұматтар не ұмтылады, немесе әр оқушыда толыққанды түрде есте сақталмайды.

2. Әр тақырыпты бастағанда нені білу қажет, қандай білім, дағды алынады және ол білім не үшін керек, және қайда қолданысқа ие болды деген сұрақтарға жауап берілмесе, онда оқушының ынтасы жойылады.

3. Геометриядағы теоремалар есептерді шығаруға пайдаланылады, ал есептер өмірде кездесетін мәселелермен байланысты.

4. Осы айтылған есептер мынандай түрлерге бөлінеді:

- есептеуге арналған есептер;

- дәлелдеуге арналған есептер;

- салу есептері.

5. Есептеу, дәлелдеу, салу үшін оқушы анықтамаларды, аксиомаларды, теоремаларды білуі және қолдана алуы қажет.

Дипломдық жұмыстың өзектілігі мен көкейтестілігі:

Оқушылар осы айтылғандарды сәтті түрде игеруі үшін пәнді оқытуға арналған әдістемелік нұсқаулар қажет, демек таңдалған тақырыбым актуалды және ғылыми тұрғыдан қарағанда жаңа әрі практикалық маңызы бар деп айтуға болады.

Әзіргі кезде бұл тақырып бойынша оқулықтарда, монографияларда және ғылыми мақалаларда біраз мәселелер көтерілген [1, 2, 3, 4, 5, 6, 7] .

Біріншісінде жалпы түрде геометрия пәнін мектептерде 1900 жылға дейін Англияда, Францияда, Италияда және Германияда оқыту үрдісі талданған (бірақ мәтін ескіріп құндылығын жойған), екіншісінде және үшіншісінде 1990-2008 жылға дейінгі 7-11 сыныптарда геометрия пәнін оқыту әдістемесі қамтылған (бірақ бағдарламасы бізге сай келмейді), төртіншісінде планиметриядан есептерді шығару әдістері қарастырылған (бірақ олар нәтиже беретіндей түрде емес), бесіншісінде үшбұрыштардың теңдік белгілеріне есеп шығару әдістері талданған (бірақ ол біздің бағдарламамызда жоқ), алтыншысында тек тікбұрышты үшбұрыштар қамтылған, жетіншісінде ұқсас үшбұрыштар мәселесі көтерілген (менің түсінігім бойынша оқулықтан асып тұрған жері шамалы) .

Керекті материал табамын деп, «Математика в школе» журналдарын 1936 жылдан бастап 2005 жылға дейінгі номерлерін шалып шықтым. Бірақ іздегенім мына кітаптардан табылды [8, 9, 10] .

Бұл кітаптардың бір ерекшелігі - пайдаланған әдебиеттерге сілтеме жасалмаған. [7] мен [8], [9] оқулықтарында материалды өз бетімен игеру үшін ұсыныстар берілген, және әр тақырып басталарда тірек ұғымдар, оқу барысында нені үйренетіндігін сонан соң анықтама әрі қарай тақырып мәтіні, сұрақтар, жаттығулар беріліпті. Кейде есептер шешу үлгісі келтіріліпті. Тура осы үрдіс [10] -да байқалады. Ал [9] -да 7-8-9-шы сынып геометрия пәнін оқытуға арналған әдістемелік нұсқаулар берілген.

Мен үшін ең үлкен ықпал етуші мәтіндер [11] кітаптан табылды. Онда 5, 6-шы тарауларда «дәлелдеуге үйрету» және «математикалық есептер» әдістемелері жалпы түрде талданған.

Дипломдық жұмыстың мақсаттарымен мәселелері:

1) Жасалған әдебиеттер шолуындағы ғалымдардың жұмыстарын 8-сыныптағы геометрия пәнін оқытуға жалпылау.

2) Жалпылау нәтижесінде 7, 8, 9 сыныпта геометрия пәнін оқытуға арналған әдістемелік нұсқауларды жазу.

3) Ол нұсқауларды практикада қолданыс табатындай ғылыми тиянақты түрге келтіру.

Дипломдық жұмыс кіріспеден, 4 тараудан, қорытындыдан және пайда-ланған әдебиеттер тізімінен тұрады. Кіріспеде жұмыстың өзектілігі, мақсаты, жаңалығы және қолдану құндылықтары ашылып айтылған.

Бейіндік оқыту.

Мемлекет басшысы республика халқына арналған «Әлеуметтік-экономикалық жаңғырту - Қазақстан дамуының басты бағыты» атты биылғы дәстүрлі Жолдауында елімізде адами капиталдың сапалы өсуіне ерекше мән беріп, «Білім беру жүйесін жаңғырту барысында біз үшін келесі іс-шараларды жүзеге асырудың маңызы зор» деп, педагогтар қауымының алдына аса маңызды және жауапкершілігі үлкен міндеттер белгіледі.

Бүгінгі таңда орта білім беру жүйесінде сапалы білім алудың қажеттілігі үдемелі артуда. Уақыт талабына сай өмір сүру үшін бәсекелестік күшейген кезде басқаша болуы мүмкін де емес. Оқыту үдерісіне қазіргі заман талабына сай технологиялар мен әдістемелерді енгізу, ғылым мен техника жетістіктерін пайдалану, этнопедагогиканың озық үлгілерін қайта жаңғыртып, қолдану, педагог мамандардың сапасын көтеру, оқушылардың функцияналдық сауаттылығын көтерумен қатар, тәрбие жұмысын жақсарту - күн тәртібінен түспейтін мәселелерге айналды. Қоғамда үлкен қозғалыс туғызған Жолдауда өскелең ұрпаққа тек білім беру ісімен шектелмей, жеткіншектеріміз игерген білімін одан әрі әлеуметтік бейімделуге ұластыруға қабілетті болуға, бұл үшін оқушылардың функционалдық сауаттылығын дамыту мақсатымен Ұлттық жұмыс жоспарын қабылдау қажеттілігі айтылған. Мерзімі - 5 жыл. Ал функционалдық сауаттылық дегеніміз - адамның өзін қоршаған ортамен қарым-қатынасқа түсе алу қабілеті және сол ортаға мүмкіндігінше жылдам бейімделе білуі мен әрекеттесе алу деңгейінің көрсеткіші. «Жақсыда жаттық жоқ», «Өзі жақсы жігітке екі адамдық орын бар», «Жақсы - Ай мен Күндей, әмбеге бірдей» деп даналық байлам жасаған бабаларымыз ұлан-ғайыр даланы мұраға алған ұрпағы кез келген ортаға бейімделе білуіне, қандай да бір жұмысты қиналмай атқаруына ерекше ден қойған. Адамзаттың данышпаны Абай да: «Зарарынан қашық болуға, пайдасына ортақ болуға тілін, оқуын, ғылымын білмек керек. Оның үшін олар дүниенің тілін білді, мұндай болды. Сен оның тілін білсең, көкірек көзің ашылады. Әрбіреудің тілін, өнерін білген кісі соныменен бірдейлік дағуасына кіреді, аса арсыздана жалынбайды», - демей ме. Сондықтан да, бүгін жаңалық ретінде ұсынылып отырған батыстық озық технологиялар мен әдіс-тәсілдердің көпшілігі қазақтың ұлттық педагогикасымен, ойшыл ағартушыларының пікірлерімен үндесіп, ұштасып жатқанын мойындағанымыз жөн.

Бүгінгі педагогика талаптары бойынша, мұғалім мен оқушы біліктілік таразысының екі басында тұрса да, тұлға ретінде «салмақтары» тең біртұтас жүйе құруға тиісті. Екі жақтың да оқу-тәрбие үдерісіне бірдей қатысып, бірдей жауапты, бірдей міндетті, бірдей ынталы болуы - ғанибет. Біз қарастырып отырған тақырып - оқушылардың өз орнын анықтауы және еркіндікке бағдарлауы дегеніміз осы. Тағы да сол хакім Абайдың: «Білімдіден шыққан сөз - талаптыға болсын кез» дейтін тұжырымына ой жүгіртсек, оның ұстаз бен шәкірт тұлғасын тең дәрежелі биіктікке көтеріп, біліктілік пен мәдениеттің тұрақтап, тіпті, дамып, береке мен бақыт көзіне айналуы екі жақтың ынта-ықыласына бірдей қатысты екенін айтып отырғанын аңғарамыз.

Қазіргі Қазақстан мектептері - кеңестік білім беру жүйесінің тікелей мұрагері. Ол дәуірде мұғалім - басқарушы, оқушы - бағынушы сипатын алып, оқу-тәрбие үдерісі баланың таңдауымен, бейімімен санаспағаны ересек буын өкілдеріне аян. Тәуелсіздіктің жиырма жылында сол кеңестік басқару әдісінің қатаң қағидалары түбірімен жойылып кетпегені де белгілі. Бұл тәртіптің салқыны мен салдарлары әлі де ұзақ уақыт сақталатыны аян. Мәселен, Қазақстан мектептерінде физика, математика, химия, геометрия сияқты күрделі пәндерді оқыту үдерісіне сыныптағы оқушылардың бәрі қатысуы міндетті дегенді естігенде АҚШ мұғалімдерінің көзі атыздай болыпты. Өйткені, өркениетті елдерде мектеп баланы оқуға мәжбүрлеу әрекетінен әлдеқашан тыйылып, оның ынтасын оятып, адамдық болмысын қалыптастыруға көшкен. Сондықтан, Нью-Йоркте физика пәні сабағына сыныптағы 20 оқушының 4-5-і ғана қатысса, мұғалім оған ренжімейді. Мұғалімнің сабақ беру әдістемесін қаласаң да, қаламасаң да, өтіп жатқан тақырып миыңа қонса да, қонбаса да сабаққа қатысуға міндеттісің деген принцип баланың болмысына үлкен нұқсан келтіретінін психолог ғалымдар нақты мысалдармен дәлелдеп отыр.

Жоғарыда аталған, Батыста кеңінен өріс алған таңдамалы оқу жүйесі, яғни, оқушының пәнді қалауы бойынша іріктеп оқуына мүмкіндік беру, олардың қарым-қабілетін ашуға ықпал ету - озық үлгі екені даусыз. Мұндай «ынтымақтастық педагогика» кең қанат жайған жерде шәкірттің ұстазға деген құрметі артады. Оқушы өзін еркін ұстайды, мұғалімге басқарушы ретінде бағыныштылықпен қарамайды, білімі озық, тәжірибесі мол, сенімді дос, әріптес ретінде қарайды. Әрине, бұл оқушы дәстүрлі пәндердің арасынан екі-үшеуін ғана таңдап оқып, басқасынан мақұрым қалсын деген сөз емес. Тұлға бастауыш мектепті тәмамдағанда 42 қаріпті танып, сөзді оқып, сөйлем құрастырып, арифметиканың төрт амалын орындай білуі қандай қажеттілік болса, дүниені тануы, өзін қоршаған табиғаттың түрлі сырлары мен құбылыстарын, өмір сүріп отырған қоғамның ерекшеліктерін, адамға, басқа да тіршілік иесіне тән қасиеттерді білуі сондай қажеттілік. Мәселен, жаңа өзіміз айтып отырған физика ғылымының әліппесін оқып, міндетті білім жүйесін меңгермесе ғарыш кеңістігі, жауын-шашынның, желдің пайда болу сырын, электр қуатының, жарықтың табиғатын, найзағайдың жарқылын, қозғалыс пен тартылыс заңдылығын, атом қуатын, т. б. жағдайларды мүлдем білмейді. Бұл - оның өмір сүру мүмкіндігін шектейді. Сондықтан, елімізде міндетті орта білім берудің мемлекеттік стандарты қабылданып, онда оқушы игеруге тиісті жалпыға ортақ талап жүйесі белгіленген. Қазақстан Республикасының «Білім туралы» заңында көрсетілгендей, тоғыз жылдық міндетті негізгі мектептің базистік оқу бағдарламасы өмірге енген-ді. Қазір республикада балалардың қабілеті мен талабына орай жұмыс істейтін түрлі бағдарлы мектептер, лицейлер мен гимназиялар көптеп саналады. Жасөспірімдерді бейіндік ыңғайына қарай оқытатын бұл мектептерде оқу үдерісі жақсы жолға қойылғаны, білім мен тәрбие сапасы жоғарылығы, Ұлттық бірыңғай тестілеуде жылма жыл үлкен нәтижеге иеленіп жүргені баршаға аян. Олардың шәкірттері облысты былай қойғанда, республикалық, халықаралық деңгейлерде өтетін пән олимпиадалары мен конкурстарда жеңімпаз атанып, мәртебеге бөленеді. Аталған мектептердің түлектері жоғары оқу орындарына да қиналмай түседі: мемлекеттік грантқа ие болатындардың басым көпшілігі солар. Яғни, алдында өзіміз озық үлгі ретінде атаған шет елдік білім ошақтарынан қазіргі кейбір мектептеріміздің ешбір кемдігі жоқ. Онда оқығандар экономикамызды жаңа сатыға көтеретін білікті маман болумен қатар қоғамды алға жылжытатын салауатты, жоғары талғамды, адамгершілік парасат-танымымен ерекшеленетін зиялы топ, ой қызметінің адамдары қатарын құрайтыны қуантады. Таяу жылдарда мектептердің 12 жылдық білім беру үдерісіне көшуі балалардың өз еркімен таңдап оқитын пәндері мен арнайы курстары білім алуға бөлінетін бүкіл уақытының тең жарымына дейін жеткізетін тағы бір батыл қадам болатыны анық. Бір өкініштісі, аталған мектептер негізінен үлкен өнеркәсіпті, әкімшілік орталықтарда шоғырланған. Ауылдардағы, әсіресе, шалғай өңірлердегі мектептер жайлы бұлай айта алмаймыз. Еліміздің Ата заңына жүгінсек, ел азаматтары, тіпті, қоғамның ең жас мүшесіне дейін, тең құқылы. Қала баласына туғызылған жағдай ауыл балдырғандарына да жасалуы керек.

Әрине, Елбасының «Қазақстан - 2030» стратегиялық бағдарламасында қамтылған бұл игілікті шаралар жүзеге асырылатыны күмәнсіз. Қазір қол жетіп отырған игілік соның алғы шарты. Дегенмен, адамдардың ғұмыры шексіз емес қой. «Көрінген таудың алыстығы жоқ» деген қағида бұл арада жүрмейді. Еліміз ауылдан шығатын келешек ұрпақтың ғана емес, бүгінгі жеткіншектердің де қабілет-қарымын, талантын толығымен пайдалануға ұмтылуы керек. Сол үшін мектеп оқушыларының функциялық сауаттылығын дамыту жөнінен үкімет тарапынан қабылданатын бесжылдық Ұлттық іс-қимылдар жоспары ауыл мектептерін де қамтуы тиісті. Сонымен бірге, бейінді оқытудың жаңа технологиясы мен әдіс-тәсілдерін білім беру үдерісіне тереңдете енгізу үшін пән мамандарының біліктілігін жетілдіруді кеңінен дамыту керек. Қазір мектепте етек алған қағазбастылықты шектеп, педагог жұмысының нәтижесін тап-тұйнақтай етіп тапсырған есебіне қарап емес, оқытқан шәкіртінің білімі мен тәрбиесіне орай бағалаған ләзім.

«Мұғалім - мектептің жүрегі» деген қанатты сөз шынайы мәніне ие болсын десек, педагог беделін көтеру және оның әлеуметтік жағдайын жақсарту бағытында нақты жұмыстар атқарылғаны жөн. Сонда ғана мектептің «ұстаз - шәкірт» жүйесіндегі өзара ықпалдастығы оңды нәтижелер береді.

2. Қарапайым геометриялық фигуралардың негізгі қасиеттері (7-8 сынып оқу бағдарламасы негізінде)

2. 1. Геомерия. Геомерияның шығу тарихы

Геометрия (көне грекше: γεωμετρία; көнегрекше: γῆ жер и көнегрекше:

μετρέω - «өлшеу») - математиканың кеңістіктік пішіндер (формалар) мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін саласы. Ғылым ретінде Ежелгі Грекияда математиканың бір бөлігі болып қалыптасқан, оның алғашқы аксиомалары Эвклидтың «Бастама» кітабында сипатталған.

Геометрия табиғатты зерттеуде, техниканы дамытуда қуатты құрал болып табылады. Ол математикалық анализге, механикаға, физикаға, астрономияға, геодезияға, картографияға, кристаллографияға, тағыда басқа ғылымдарға елеулі ықпал етеді.

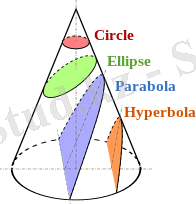
Конустың қималары: шар, эллипс, парабола, гипербола

Фигуралар - кеңістіктік пішіндер болып есептеледі. Геометрия тұрғысынан сызық - “сым” емес, шар - “домалақ дене” емес, олардың барлығы да - кеңістіктік пішіндер. Ал кеңістіктік қатынастар - фигуралардың мөлшері мен орналасуын анықтайды. Мысалы, центрлері ортақ, радиустары 3 см және 5 см шеңберлер қиылыспайды, “біріншісі екіншісінің ішінде жатады” дегенде - шеңберлердің мөлшері мен орналасуы жөнінде айтылып тұр. Мұнда бірінші шеңбер - кішісі, екіншісі - үлкені, біріншісі екіншісінің ішінде орналасқан. Осыған орай кеңістіктік қатынастар “үлкен”, “кіші”, “ішінде”, “сыртында” сөздері арқылы анықталған. “Тең”, “параллель”, тағыда басқа сөздер де кеңістіктік қатынастарды сипаттайды.

Дененің шекарасы - бет. Ол денені қаптап, қоршап, шектеп, кеңістіктен бөліп тұрады. Бет шектеусіз жұқа болып есептеледі. Жіңішке жіп, бір тал қыл, сәуле, сым, тағыда басқа негізінде шектеусіз жіңішке сызық ұғымы шыққан. Геометриялық денелерді ойша топшылап, шектеусіз кішірейте беруге болады. Осыдан нүкте ұғымы шығады. Нүкте дененің әбден кішірейіп, тоқтаған шектік жағдайы деп есептеледі. Геометрия тұрғысынан алғанда нүктені одан әрі кішірейтуге болмайды. Геометриялық денелердің, беттердің, сызықтардың және нүктелердің кез келген жиыны фигура деп аталады. Айтылып отырған негізгі ұғымдар - нүкте, сызық, бет, дене дүниедегі заттардан (яғни, материядан) алынған. Бірақ материяның физикалық қасиеттерінен абстракцияланған. Мысалы, призма жөніндегі теоремаларды ағаштан, тастан, металдан жасалған призмалардың бәріне де және әрдайым қолдана беруге болады. Геометрия алғашқы кезде фигуралардың мөлшерлерін, өзара орналасу тәртібін, бір түрден екінші түрге көшу жолдарын зерттейтін ғылым болды. Онда фигуралардың түрлендірілуі берілген фигура мен кейін пайда болған фигураның арасындағы белгілі бір қатынастар ретінде түсіндірілді. Мұндай түсінік осы күнгі геометрияда да бар. Алайда қазіргі геометрия байырғы түсініктер шебінен ұзап шығып кетті. Соңғы ғасырларда геометрияның үйреншікті ұғымдары мен қағидаларын талдау, жалпылау, жартылай өзгерту және одан әрі абстракциялау нәтижесінде математиканың бірталай жемісті теориялары шықты. Геометрияның жаңа салаларының көпшілігі ертеде қалыптасқан дәстүрлі салаларына мүлдем ұқсамайды. Мысалы, Георг Фридрих Бернхард Риман кеңістігіндегі “ара қашықтық”, Гильберт кеңістігіндегі “призма” ұғымдарын, жалпы түрде алғанда, ешқандай сурет, модель бойынша сипаттауға болмайды. Оларды дүниеде кездесетін нақты нәрселердің пішіндері мен қатынастары арқылы түсіндіру өте қиын. Сөйтсе де, Геометрияның байырғы салалары жаңа салаларының қарапайым дербес көріністері болып табылады. Сөз болып отырған жаңа теориялардың қайшылықсыздығы мұқият дәлелденген және олар күмәнсіз. Соңғы салалар да, тарихи жағынан геометрия шаңырағының астында туғандықтан және олардың заңдары бұрынғы геометрияның заңдарына сырттай ұқсас болғандықтан, геометрияға жатқызылады. Сөйтіп, геометрияның өрісі мүлдем кеңейіп кетті. Оның жоғарыда келтірілген анықтамасына “сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін” деген сөздер сондықтан қосылған. Осылай кең мағынада түсінген жағдайда ғана геометрия математиканың көптеген саласымен астасып жатады.

Геометрияның шығу тарихы

Геометрия - ерте замандарда шыққан ғылымдардың бірі, оның тарихы да әріректен басталады. Сапалық өзгерістерге ұшырап, жаңа сатыларға көтерілу дәрежесіне қарай Геометрияның даму жолын 4 дәуірге бөлуге болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.