Дирихле және локалды емес шеттік шарттардағы Коши-Риман операторының спектрлік есебі: сингулярлық интегралдық теңдеулерге редукция, индекс есептеу және Фредгольмдік редукция


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:
Мазмұны
Коши-Риман дифференциалдық амалынан туындайтын
операторлар туралы мәліметтер . . .
Спектральдық есептің бір сингулярлық интегралдық
тендеуге редукциялануы . . .
Сингулярлық интегралдық теңдеудің индексін
есептеу . . .
Сингулярлық интегралдық теңдеудің 2-текті интегралдық
Фредгольм теңдеуіне редукциялануы . . .
Локалды емес шеттік шарттарымен Коши - Риман
операторының спектральды есептерімен байланысқан
квазисингулярлы интегралды теңдеулер
Фредгольмнің интегралдық теңдеулеріне
мәлімет . . .
Кіріспе
Соңғы уақыттарда математиктердің назарын дербес туындылы теңдеулермен берілген есептердің қосымша шекаралық шарттарының ізделінді функциямен байланысы туралы мәліметтер алаңдатуда. Ізделінді функциялар қарастырылған аймақтың және шекарада жатқан әртүрлі айнымалы нүктелердің есептелуінен тәуелді болатындығына күмән келтірілмейді. Алынатын және алынған нәтижелердің теориялық мағынасы келесі түрдегі қолданылуларға байланысты қызықтыра бастады.
Мысалы: шекаралық шарттар динамикасының есептерін математикалық модельдегенде, сондай-ақ плазма, жылу өткізгіштік теориясында, лазер зерттегенде, өсімдіктің тамырындағы ылғалдылыққа болжам жасағанда, бактериялардың даму процесін зерттегенде, жасушалардың көбею процесін
зерттегенде пайда болады. Кейбір жағдайларда (жоғары өткізгіштер физикасында, радиациялық көшіру, судың биосферадағы ластануының таралу процесі, популяциялық генетика және көптеген биологиялық проблемаларда) шекаралық шарттар интегралдық формада болады және айтылып отырған мәселелерге келтіріледі. Ең қарапайым шекаралық шарттардың мысалдары жылу өткізгіштік проблемасынан пайда болғандығын 1922 жылы В. А. Стеклов көрсетті, ал газдар динамикасындағы шекаралық шарттарды 1956 жылы Ф. И. Франкль көрсетті. 1969 жылы А. М. Нахушев осы түрдегі бірнеше есепті қойды. Ол үшін «Ығыстырылған » термині қолданылды. Осы 1969 жылы алғаш рет А. В. Бицадзе және А. А. Самарскийдің «аймақ ішінде ығыстырылған» есебі қойылды. Соңғы публикациялардың мазмұны дербес туындылы дифференциалдық теңдеу теориясы үшін ығыстырылған шектік есеп жаңалығын ашты. Бұл публикацияларда барлық жағдай жеткілікті түрде қарастырылған. Мұнда аз қарастырылғанмен дербестік туралы, меншікті мән туралы есеп немесе оның аналитикалық бейнесі туралы маңызды сұрақтар қарастырылған. Қазірде қолданылып жүрген функционалдық анализ және модельді теңдеуде интегралдық түрлендіру әдісі жоғарыдағыдай құнды мәлімет алуға жеткіліксіз. Басқаша айтқанда, дербес туындылы дифференциалдық теңдеудің меншікті мәндері есебінің шешімін қарапайым дифференциалдық теңдеу жағдайына ұқсас алуға болатынына үміттенуге болады.Дербес туындылы теңдеу үшін жоғарыдағы сұрақтар өте қатаң шектелген операторларды зерттеуге алып келді. Есептің қойылыуының дұрыстығын анықтағанда және «классикалық емес» теңдеу үшін өзіндік қасиетін зерттегенде идеалды модельді талқылаудан, мысалы, тұрақты коэффициентті теңдеуді талқылаудан бастаған қолайлы.
1. 1 Коши-Риман дифференциалдық амалынан туындайтын
операторлар туралы мәліметтер
Жалпы біз комплекс жазықтықта жұмыс істейміз.
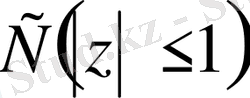 бірлік дөңгелектің бойындағы бүкіл үзіліссіз функциялар кеңістігінде берілген Коши - Риман дифференциалдық амалынан туындайтын К операторын қарастырамыз:
бірлік дөңгелектің бойындағы бүкіл үзіліссіз функциялар кеңістігінде берілген Коши - Риман дифференциалдық амалынан туындайтын К операторын қарастырамыз:
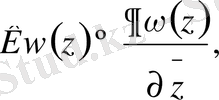
 (1. 1. 1)
(1. 1. 1)
мұндағы z-комплекс айнымалы, яғни
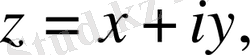
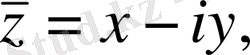
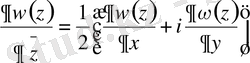 - Коши - Риман дифференциалдық амалы. Бұлар бізге комплекс айнымалы функциялар теориясынан белгілі.
- Коши - Риман дифференциалдық амалы. Бұлар бізге комплекс айнымалы функциялар теориясынан белгілі.
Енді Коши - Риман дифференциалдық амалынан туындайтын К операторы
 функциясына әсер етсіни делік. Сонда
функциясына әсер етсіни делік. Сонда
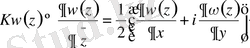
Жалпы, кез келген оператор өзінің анықталу аймағымен қоса беріледі, яғни
Алдын ала К операторының резольвенттік жиыны
 бос жиын емес деп, ұйғарсақ
бос жиын емес деп, ұйғарсақ
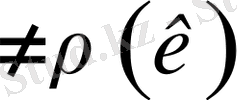
Олай болса ол резольвенттік жиында ең болмағанда бір элемент жатады

 кері операторы (1. 1. 2)
кері операторы (1. 1. 2)
Ал, енді біздің қарастырып отырғанымыз осы Коши - Риман дифференциалдық амалынан туындайтын операторлардың меншікті мәндерін, яғни спектрлерін табуға арналған есебін қарастырайық
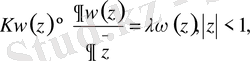 (1. 1. 3)
(1. 1. 3)
Мұндағы К - Коши - Риман дифференциалдық операторы. К операторының мұндағы
 функциясына әсері. Коши - Риман дифференциалдық есебінің тарихы 1922 жылы В. А. Стекловтан басталады.
функциясына әсері. Коши - Риман дифференциалдық есебінің тарихы 1922 жылы В. А. Стекловтан басталады.
Сонымен, 1969 жылы А. М. Нахушев локальді емес шекаралық шаттардың қойылуын талап етті. Сол кезде «Қандай жағдайда (3) теңдеуінің нөлдік емес шешімі бар және ол жалғыз болады?» - деген мәселелерді қойды. Міне, сол жылы, яғни 1969 жылы тағы да мынадай шекаралық шарт пайда болды. Оны тапқан А. В. Бицадзе, А. А. Самарский. Коши - Риман дифференциалдық амалынан туындайтын көптеген әр түрлі есептер бар. Олар: Риман - Гильберт есебі, түйіндесу есебі, тағы басқа. Мұндай есептермен И. Н. Векуа және оның шәкірттері; ал Қазақстанда М. Өтелбаев, Блиев Н. К, Тұңғаратов А. Б., Бияров, Б. Кангужин, Т. Ш. Кальменов және тағы басқа осы ғалымдардың шәкірттері айналысқан.
Ал біздің қарастыратынымыз Коши - Риман дифференциалдық операторының меншікті мәндерге арналған есебі. «
 - ға байланысты (1. 1. 3) теңдеуінің қай кезде нөлдік емес жалғыз шешімі болады?» - деген сұрақты алғаш рет Мұхтарбай Өтелбаев және оның шәкірті А. Н. Шыныбеков, 1982 жылы жариялады [4] . Осы жұмыста [4] М. Өтелбаевтың мынадай теоремасы бар:
- ға байланысты (1. 1. 3) теңдеуінің қай кезде нөлдік емес жалғыз шешімі болады?» - деген сұрақты алғаш рет Мұхтарбай Өтелбаев және оның шәкірті А. Н. Шыныбеков, 1982 жылы жариялады [4] . Осы жұмыста [4] М. Өтелбаевтың мынадай теоремасы бар:
Теорема 1 (М. Өтелбаев) . К операторы үшін мынадай теңдеу қарастырамыз:
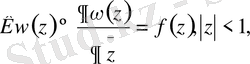 (1. 1. 4)
(1. 1. 4)
(1. 1. 4) теңдеуінің шешімі бар және ол жалғыз болуы үшін К операторының анықталу аймағы келесі түрде берілу керек:
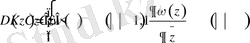
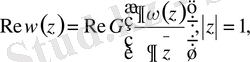
 (1. 1. 5)
(1. 1. 5)
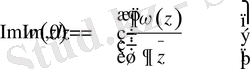
 (1. 1. 6)
(1. 1. 6)
Мұндағы
 операторы:
операторы:
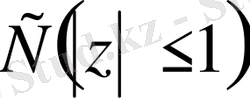 бірлік дөңгелектегі бүкіл үзіліссіз функциялар кеңістігін, Н-голоморфты функциялар кеңістігіне бейнелейтін, сызықты, шенелген оператор.
бірлік дөңгелектегі бүкіл үзіліссіз функциялар кеңістігін, Н-голоморфты функциялар кеңістігіне бейнелейтін, сызықты, шенелген оператор.

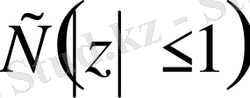

Ал,
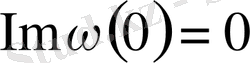 яғни
яғни
 нүктесіндегі жорамал бөліктерінің мәні нөлге тең болатын функцияларды комплекс сандар жиынына бейнелейтін, сызықты, шенелген
нүктесіндегі жорамал бөліктерінің мәні нөлге тең болатын функцияларды комплекс сандар жиынына бейнелейтін, сызықты, шенелген
 -функционалы. Яғни, осы табылған
-функционалы. Яғни, осы табылған
 -операторы мен
-операторы мен
 -функционалы арқылы К операторының анықталу аймағы көрсетіледі екен.
-функционалы арқылы К операторының анықталу аймағы көрсетіледі екен.
 -шекаралық оператор,
-шекаралық оператор,
 - шекаралық функционал.
- шекаралық функционал.
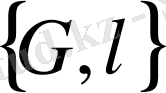 шекаралық жұптар деп аталады.
шекаралық жұптар деп аталады.
Әрбір К сызықты операторы үшін сәйкес
шекаралық жұптары табылып отырады. Керісінше, әрбір
шекаралық жұптары үшін, сәйкес К операторы табылып отырады.
Бұл (4) теңдеуінің шешімінің бар екенін және оның жалғыздығын қамтамасыз ететін шекаралық шарт болып табылады. Яғни, міне осындай шекаралық шарттар қойылғанда ғана (4) операторлық теңдеуі үшін қойылған есептің корректілігі қамтамасыз етіледі.
М. Өтелбаев мағынасында мұндай шартты корректі сығылу шарты деп атайды. Коши-Риман операторының меншікті мәндері туралы тереңірек мәліметтерге Степанец, В. А. Михайлец сияқты Украин математиктері қол жеткізді. 1989 жылы В. А. Михайлецтің докторлық диссертациясында [7] шекаралық
операторының спектрінің қасиетіне байланысты К операторының спектрі туралы мәлімет алынған. Ол былай :
Егер
операторының спектрі дискретті болса, онда К операторының спектрі де дискретті болады. Ал, егер
операторының спектрі үзіліссіз болса, онда К операторының спектрі де үзіліссіз болады.
Дегенмен, бұл нәтижелер жалпы түрдегі мәліметтер болады. Ал, біздің қарастырып отырғанымыз
және
түрін нақты етіп алу. "Нақты түрін қайдан алдың?"-деген сұраққа былайша жауап берейік. Айтып өткеніміздей 1982 жылғы М. Өтелбаевтың және А. Н. Шыныбековтың [4] жұмысында осындай шекаралық шарттардың бірнеше мысалдары келтірілген. Ең қарапайым түрі біртекті шекаралық шарттарымен берілген Дирихле есебі үшін Коши-Риман дифференциалдық операторының меншікті мәндерін зерттеу болып табылады.
1. 2 Спектралдық есептің бір сингулярлық интегралдық теңдеуге редукциялануы
Бұл жұмыста біртекті шекаралық шарттарымен берілген Дирихле есебі үшін Коши-Риман дифференциалдық операторының меншікті мәндерін зерттеу есебі қарастырылған, яғни
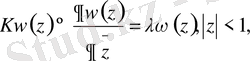
 (1. 2. 1)
(1. 2. 1)
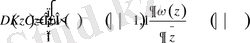
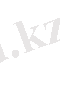
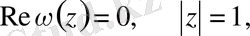 (1. 2. 2)
(1. 2. 2)
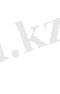
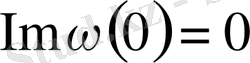 ,
,
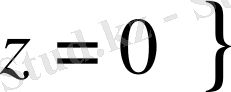 (1. 2. 3)
(1. 2. 3)
мұндағы
 спектральдық параметр
спектральдық параметр
Есептің қойылымы
:
 С-ның қандай мәндерінде (1. 2. 1) операторлық теңдеуінің нөлден өзгеше шешімдері бар болады?
С-ның қандай мәндерінде (1. 2. 1) операторлық теңдеуінің нөлден өзгеше шешімдері бар болады?
Шешуі
: Кез келген дербес туындылы дифференциалдық теңдеудің жалпы шешімі шекарада, яғни
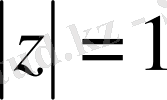 шеңбердің бойында, өзінің нақты бөлігі және нөл нүктесіндегі жорамал бөлігі арқылы Шварц формуласымен өрнектеледі
шеңбердің бойында, өзінің нақты бөлігі және нөл нүктесіндегі жорамал бөлігі арқылы Шварц формуласымен өрнектеледі
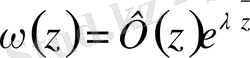 (1. 2. 4)
(1. 2. 4)
мұнда
дөңгелектегі функция. Біздің есебіміздің голоморфтығына көз жеткізу үшін (1. 2. 1 ) -теңдіктің екі жағын да
ға көбейтеміз. Сонда
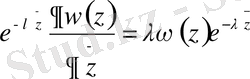
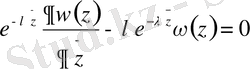
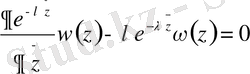
Ал, мұндағы
болғандықтан, оны орнына апарып қойсақ келесі теңдікті аламыз.
,
,
.
Бұл жерден
көбейтіндісі
дөңгелекте голоморфты функция болатындығын көреміз.
Теорема 2 : Кез келген голоморфты функцияны - өзінің шекарадағы нақты бөлігі және ішкі нүктедегі жорамал бөлігі арқылы Шварц интегралдық формуласы бойынша жіктеуге болады.
Олай болса, Ф(
 ) голоморфты функциясын Шварц интегралдық формуласы бойынша былай жазамыз:
) голоморфты функциясын Шварц интегралдық формуласы бойынша былай жазамыз:
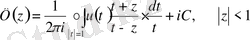
мұндағы
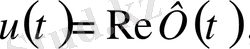
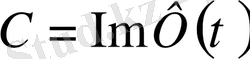 .
.
Сондықтан (1. 2. 4) - формула келесі түрге енеді:
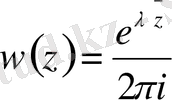
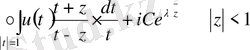
Шварц формуласы дөңгелектің ішіне арналған формула, ал бізге керегі шекарада, яғни
 шеңбердің бойында: демек, бұл жерде Сохоцкий - Племель [5] түрлендіру формуласын пайдаланамыз.
шеңбердің бойында: демек, бұл жерде Сохоцкий - Племель [5] түрлендіру формуласын пайдаланамыз.
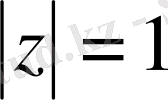 шеңбердің бойында Шварц формуласын аламыз.
шеңбердің бойында Шварц формуласын аламыз.
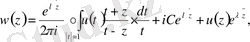
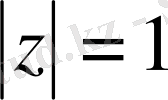
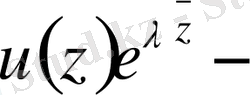
 функциясының шекарадағы секірісі.
функциясының шекарадағы секірісі.
Дәлелдеу . Соңғы формула (1. 2. 1) теңдеуінің жалпы шешімі, енді оны (1. 2. 2) шекаралық шартқа қоямыз. Сонда шығатыны
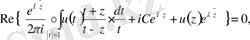
Комплекс санның нақты бөлігін
 болған жағдайда комплекс санның және оның түйіндесінің жарты қосындысы түрінде ашып жазып көрсетуге болады.
болған жағдайда комплекс санның және оның түйіндесінің жарты қосындысы түрінде ашып жазып көрсетуге болады.
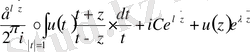

Бұдан шығатыны
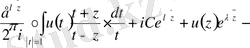
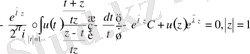
Соңғы теңдеуді былай түрлендіреміз:
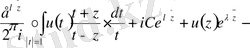
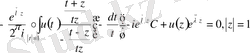
Яғни
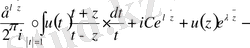
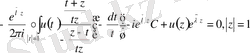
Бұдан
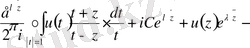
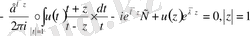
Немесе
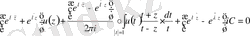 ,
,
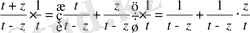
екендігін ескеріп және сингулярлы бөлігін белгілеп, канондық формада жазамыз.

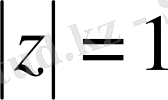 (1. 2. 5)
(1. 2. 5)
Енді (1. 2. 3) шартты пайдаланып, С тұрақтыны табамыз. Сонда
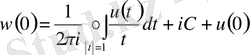

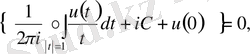
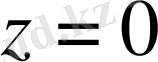
Бізге комплекс айнымалы функциялар теориясынан мынадай формула белгілі
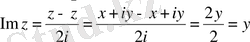
Осы формуланы пайдаланып, соңғы теңдікті ашып жазып көрсететін болсақ
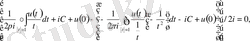
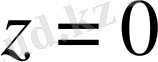
Ал бұдан шығатыны
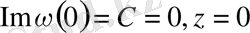 (1. 2. 6)
(1. 2. 6)
Осы табылған С - ның мәнін (1. 2. 5) - теңдікке қоятын болсақ

немесе

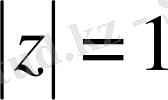
Бұдан
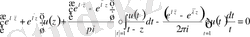 ,
,
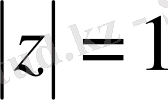
Немесе
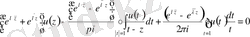 ,
,
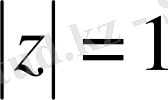
Егер соңғы теңдікте мынадай белгілеулер енгізетін болсақ

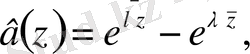
Онда
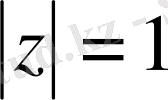 шеңбердің бойында анықталған нақты мәнді
шеңбердің бойында анықталған нақты мәнді
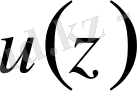 функциясы үшін келесі сингулярлық интегралдық теңдеуге келеді екенбіз
функциясы үшін келесі сингулярлық интегралдық теңдеуге келеді екенбіз

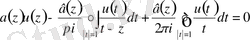 (1. 2. 7)
(1. 2. 7)
Осы дәлелдеген фактіні бекітейік.
Теорема 3 : (1. 2. 2), (1. 2. 3) - біртекті шекаралық шарттарымен берілген (1. 2. 1) -Коши - Риман дифференциалдық операторының спектрлерін зерттеуге арналған Дирихле есебі келесі түрдегі сингулярлық интегралдық теңдеуге редукцияланады.
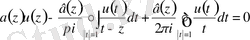
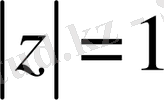
мұндағы
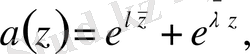
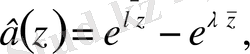
Осы (1. 2. 7) сингулярлық интегралдық теңдеудің спектрлері туралы мәлімет алу (1. 2. 1), (1. 2. 2), (1. 2. 3) - Коши - Риман дифференциалдық операторының спектрлерін табумен эквивалентті.

(1. 2. 7) теңдеуде - сингулярлық интегралдық теңдеудің бас бөлігі, ал
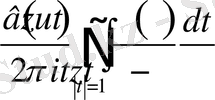 - сингулярлық интегралдық теңдеудің ядролық бөлігі деп аталады.
- сингулярлық интегралдық теңдеудің ядролық бөлігі деп аталады.
1. 3 Сингулярлық интегралдық теңдеудің индексін есептеу
 келесі формуламен (1. 2. 7) теңдеуінің индексі есептеледі.
келесі формуламен (1. 2. 7) теңдеуінің индексі есептеледі.
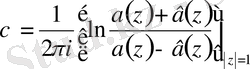 ,
,
мұндағы
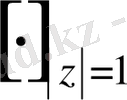 квадрат жақшаға алынған функцияның бірлік шеңбер бойымен оң бағытта жүру кезіндегі өсімшесі. Осы формулаға
квадрат жақшаға алынған функцияның бірлік шеңбер бойымен оң бағытта жүру кезіндегі өсімшесі. Осы формулаға
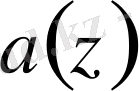 пен
пен
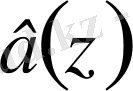 - мәндерін қойсақ
- мәндерін қойсақ
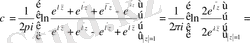
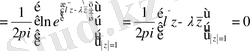
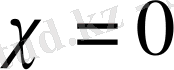 екендігіне көз жеткізу үшін
екендігіне көз жеткізу үшін
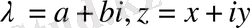 десек
десек
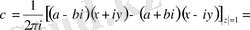
=

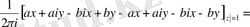
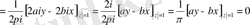
немесе
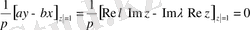
Сингулярлық интегралдық теңдеудің индексі
 нөлге тең.
нөлге тең.
1. 4 Сингулярлық интегралдық теңдеудің 2-текті Фредгольм теңдеуіне редукциялануы
Индекс
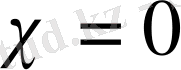 болғандықтан, (1. 2. 7) сингулярлық интегралдық теңдеуі 2 - текті Фредгольм теңдеуіне эквивалентті болады
болғандықтан, (1. 2. 7) сингулярлық интегралдық теңдеуі 2 - текті Фредгольм теңдеуіне эквивалентті болады
 .
.
 арқылы (1. 2. 7) теңдеудің сол жағын белгілеп алайық. Егер
арқылы (1. 2. 7) теңдеудің сол жағын белгілеп алайық. Егер
 (1. 2. 7) -сингулярлық интегралдық теңдеудің шешімі болса, бірлік шеңберде нолге теңбе - тең келесі өрнекті қарастырамыз
(1. 2. 7) -сингулярлық интегралдық теңдеудің шешімі болса, бірлік шеңберде нолге теңбе - тең келесі өрнекті қарастырамыз
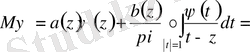
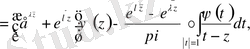
 өрнегін түрлендіріп, Пуанкаре - Бертран
өрнегін түрлендіріп, Пуанкаре - Бертран
 орын ауыстыру формуласын пайдалансақ
орын ауыстыру формуласын пайдалансақ


Нәтижеде
 болғанда алатынымыз
болғанда алатынымыз
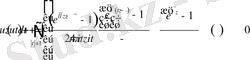 (1. 4. 1)
(1. 4. 1)
Ал, бұл 2 - текті интегралдық Фредгольм теңдеуі
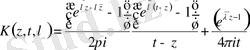
деп, белгілесек, ол
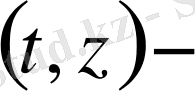 дан тәуелді үзіліссіз ядро екенін көреміз.
дан тәуелді үзіліссіз ядро екенін көреміз.
Сонымен, (1. 2. 1), (1. 2. 2), (1. 2. 3) спектральдық есебі 2 - текті Фредгольм теңдеуіне редукциаланды.

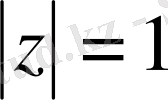
Яғни (1. 2. 1), (1. 2. 2), (1. 2. 3) есебі Фредгольмді болып табылады.
2 Локалды емес шеттік шарттарымен берілген Коши - Риман
операторының спектральды есептерімен байланысқан
квазисингулярлы интегралдық теңдеулер
2. 1 Квазисингулярлы интегралдық теңдеуге локалды емес шеттік шарттармен берілген Коши - Риман дифференциалдық
операторының меншікті мәндерін зерттеу есебін редукциялау
Локалды емес шеттік шарттарымен берілген Коши -Риман дифференциалдық операторының меншікті мәндерін зерттеуге арналған есепті қарастырайық.
1 бөлімдегі нәтижелерді ескере отырып операторлық теңдеуді
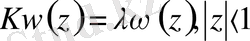
мына
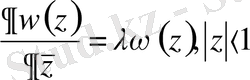
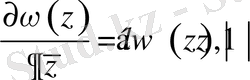 (2. 1. 1)
(2. 1. 1)
түрінде жазамыз.
Локалды емес шеттік шарттарымен берілген
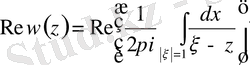
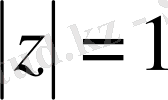 (2. 1. 2)
(2. 1. 2)
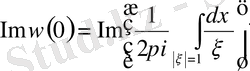 (2. 1. 3)
(2. 1. 3)
мұнда
 - спектральді параметр.
- спектральді параметр.
Мұндағы есепті (2. 1. 1) операторлық теңдеуде нөлдік емес шешімдерге ие болып
 комплекс санын табумен аяқталады.
комплекс санын табумен аяқталады.
Дербес туындылы дифференциалдық теңдеудің жалпы
 шешімі келесі түрде болады.
шешімі келесі түрде болады.

 (2. 1. 4)
(2. 1. 4)
Мұнда

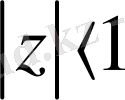 шеңберіндегі голоморфты функция.
шеңберіндегі голоморфты функция.
Шындығында, (2. 1. 1) теңдеудің екі жағында
 - ке көбейтсек
- ке көбейтсек

аламыз. Демек

мына

теңдікке ие болады.
Бұдан
 көбейтіндісі
көбейтіндісі
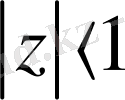 шеңберіндегі голоморфты функция болатындығы туындайды. Голоморфты функция Шварц интегралды формуласы бойынша өзінің шекаралық нақты бөлігі арқылы және өзінің жорамал бөлігі арқылы ішкі нүктесі нөл болып келесі түрде өрнектеледі:
шеңберіндегі голоморфты функция болатындығы туындайды. Голоморфты функция Шварц интегралды формуласы бойынша өзінің шекаралық нақты бөлігі арқылы және өзінің жорамал бөлігі арқылы ішкі нүктесі нөл болып келесі түрде өрнектеледі:

мұнда
(2. 1. 4) формула салдарынан

түрде болады.
Соңғы формула (2. 1. 1) теңдеудің жалпы шешімі болады, яғни (2. 1. 2) -ге шеттік шарттарды қоямыз. ([5], 55 бет) . Сохоцкий-Племеля формуласын қолдана отырып,
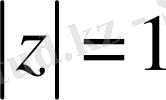 болғанда шеттік шарттар мәнінің шешімін табамыз
болғанда шеттік шарттар мәнінің шешімін табамыз

мұнда
 - шекарадағы секіру функциясы.
- шекарадағы секіру функциясы.
Сонда келесі қатынасқа ие боламыз
Пуанкаре-Бертран формуласынан пайдаланып ([5], 102 бет) интегралдау кезегін алмастырсақ, соңғы теңдікті
(2. 1. 5)
 (2. 1. 6)
(2. 1. 6)
Демек
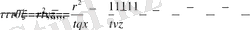 ,
,
болса, онда қалындылар көмегімен (2. 1. 6) интегралда есептеуге болады,
 белгісіз функция құрамында жоқ. Бұдан келесі салардың бар болуы орын алады.
белгісіз функция құрамында жоқ. Бұдан келесі салардың бар болуы орын алады.
Салдар
.
 ерекше нүктеде қалынды
ерекше нүктеде қалынды
 ден интеграл
ден интеграл
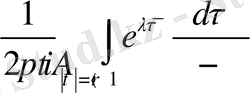
формуласы бойынша есептеледі.

Осы салдарды негізге ала отырып интеграл астындағы функциядан қалындыны есептейміз, яғни
 нүктесінде ерекшеге ие болатын. Басқа да ерекше нүктелерде интеграл астындағы функциядан қалындығын оңай есептеуге болады, сонымен бірінші ретті полюстің ерекше түріне ие болады.
нүктесінде ерекшеге ие болатын. Басқа да ерекше нүктелерде интеграл астындағы функциядан қалындығын оңай есептеуге болады, сонымен бірінші ретті полюстің ерекше түріне ие болады.




Сонымен (2. 1. 6) теңдікті келесі түрде
 (2. 1. 7)
(2. 1. 7)
Комплекс санының нақты бөлігін комплекс санының жарты қосынды және оның түйіндесі түрінде жазамыз, сонда
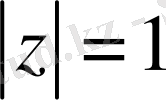 келесі қатынасқа көшеміз
келесі қатынасқа көшеміз

Соңғы қатынасты келесі түрде түрлендіреміз
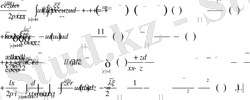
Сингулярлы бөлігін бөле отырып, алынған қатынастың канондық түрін жазамыз
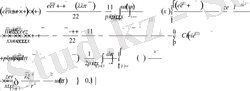
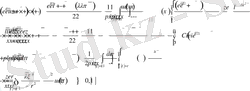 (2. 1. 8)
(2. 1. 8)
(2. 1. 8) дегі С-ты жою үшін (2. 1. 3) -гі шеттік шарттарды қолданамыз. Құрамында белгісіз
 функция болмайтын және (2. 1. 3) -ге шеттік шарттарды қолданғаннан соң алынған теңдіктен интеграл есептейміз.
функция болмайтын және (2. 1. 3) -ге шеттік шарттарды қолданғаннан соң алынған теңдіктен интеграл есептейміз.
Сондай-ақ алынған интеграл мәнін қоя отырып және ұқсас мүшелерді топтай отырып, нақты тұрақтылар үшін формуланы аламыз.
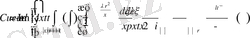
Бұдан (2. 1. 8) қатынастан С тұрақтыны жоюға болады. Жорамал бөлікті комплекс санмен оның түйіндесінің айырымы түрінде жаза отырып, интегралдық теңдеуді аламыз.

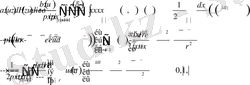
 (2. 1. 9)
(2. 1. 9)
Демек, (2. 1. 1), (2. 1. 2), (2. 1. 3) есептері Н. С. Иманбаевтың [13] (2. 1. 9) квазисингулярлы интегралдық теңеулерінде көрсетілген. Бұл факт келесі теоремада тұжырымдалады.
Теорема 2. 1 [7] . (2. 1. 1), (2. 1. 2), (2. 1. 3) есептерінің шешімі келесі формуламен анықталады.

демек
 нақты функция үшін
нақты функция үшін
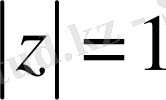 шеңберінде келесі сингулярлы интегралдық теңдеулер дұрыс.
шеңберінде келесі сингулярлы интегралдық теңдеулер дұрыс.
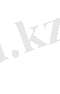 (2. 1. 10)
(2. 1. 10)
мұнда
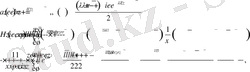
 - үзіліссіз ядро.
- үзіліссіз ядро.
Жалпы теңдеудегі С тұрақтыны келесі түрде көреміз.
2. 2 Квазисингулярлы интегралды теңдеулердің нетерлігі және индексті есептеу
 функционалдық кеңістікте Коши-Риман операторлық теңдеуін қарастырайық.
функционалдық кеңістікте Коши-Риман операторлық теңдеуін қарастырайық.
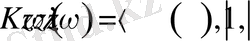
мұнда
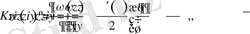
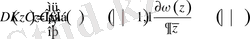
анықталу облысымен локалды емес шекаралық шарттармен
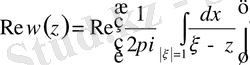
 (2. 1. 2)
(2. 1. 2)
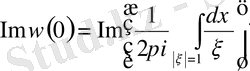 (2. 1. 3)
(2. 1. 3)
мұндағы
 - спектралдық параметр.
- спектралдық параметр.
2. 1. 1 бөлімше (2. 1. 1), (2. 1. 2), (2. 1. 3) есептер

мұнда
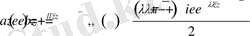

 -үзіліссіз ядро.
-үзіліссіз ядро.
[2] және [3] - н белгілі болғандай сингулярлы интегралды теңдеуді индексі бүтін сан деп аталады

мұнда
 квадратты жақшамен біткен бірлік шеңберде оң бағытпен сағат тіліне қарсы айналғандағы функция өсімшесі немесе
квадратты жақшамен біткен бірлік шеңберде оң бағытпен сағат тіліне қарсы айналғандағы функция өсімшесі немесе

 (2. 2. 1)
(2. 2. 1)
Квазисингулярлы интегралдық теңдеуде (2. 1. 10)
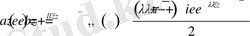
теңдеудің нетерлігі
 теңсіздігімен немесе
теңсіздігімен немесе
 үшін анықталады. Бұл схема бойынша нетерлікті және квасингулярлы интегралдық теңдеулердің индексін есептейміз (2. 1. 10) .
үшін анықталады. Бұл схема бойынша нетерлікті және квасингулярлы интегралдық теңдеулердің индексін есептейміз (2. 1. 10) .
Сонымен
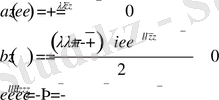
орындалғандағы нетерлік бұзылады немесе
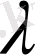 спектральды параметрі келесі бағалаудан орын алады
спектральды параметрі келесі бағалаудан орын алады
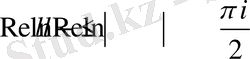
Сонда бұдан
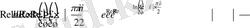
туындайды.
Демек
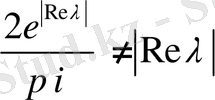 . Сонымен
. Сонымен
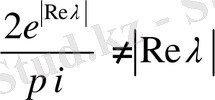
болғанда нетерлік кепіл береді.
Енді (2. 1. 10) квазисингулярлы интегралдық теңдеудін индексін есептеуге көшейік (2. 2. 1)
 шамасы
шамасы
 z- тен тәуелсіз болса, өсімшесі нөль болады.
z- тен тәуелсіз болса, өсімшесі нөль болады.

квазисингулярлы интегралдық теңдеудің (2. 1. 10)
 индекс нөлге тең.
индекс нөлге тең.
Енді келесі тұжырымдарда орын орын болады.
Тұжырым 1.
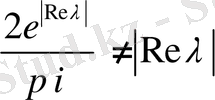
шарты орындалғанда (2. 1. 10) квазисингулярлы интегралдық теңдеулер нетерлі болып, оның индекс
 нөлге тең болады.
нөлге тең болады.
2. 3 Фредгольмның интегралдық теңдеулеріне мәлімет
æ=0 индексі нөлге тең болса, онда осыдан шығатын сингулярлы интегралдық теңдеу Фредгольмның интегралдық теңдеуіне эквивалентті [6] . Бұл параграфта 4 параграфтің нәтижесіне сәйкес сингулярлы интегралдық теңдеуді Фредгольм теңдеуіне келтіреміз. 3 параграфтегі 1 теоремада
 болғанда келесі функциялар енгізілген.
болғанда келесі функциялар енгізілген.
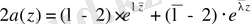 ,
,
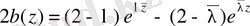 ,
,
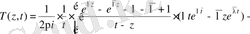
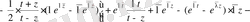

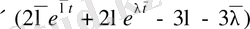 .
.
Белгілеу енгіземіз
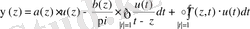
Егер
 сингулярлы интегралдық теңдеудің 3 параграфтегі 1 теоремадан келіп шығатын шешімі болса, бірлік шеңберде нөлге тең болатын өрнекті қарастырамыз.
сингулярлы интегралдық теңдеудің 3 параграфтегі 1 теоремадан келіп шығатын шешімі болса, бірлік шеңберде нөлге тең болатын өрнекті қарастырамыз.
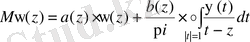
Пуанкаре-Бертрана Пуанкаре-Бертран формуласын қолданып
 өрнегін түрлендіреміз
өрнегін түрлендіреміз
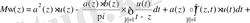
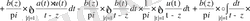
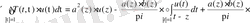
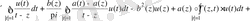
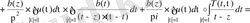
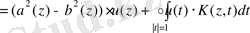 ,
,
Мұндағы
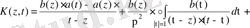
 .
.
Келесі екі лемма тікелей есептеу арқылы алынады.
♦ Лемма 1.
 болғанда мына формула орынды:
болғанда мына формула орынды:
 ,
,
Дәлелдеу. 1 лемманы дәлелдеу үшін екі интегралды есептейміз.
Интегралды есептейік

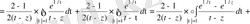
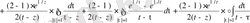 .
.
Функция ерекше нүктеге
 ие және
ие және
 ,
,
 болғанда ерекшеліктері ескеріледі.
болғанда ерекшеліктері ескеріледі.
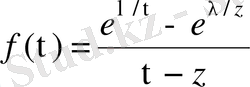 ,
,
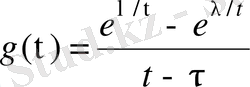
Сондықтан осы функциялардың интегралы алу теоремасы бойынша есептелінеді.
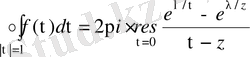 ,
,
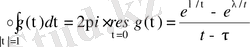 .
.
Мыналар белгілі
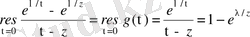 .
.
Екінші жағынан Сохоцки-Племел формуласын пайдаланып, бастапқы тағайындалған мағынасы бойынша интегралды есептейміз.
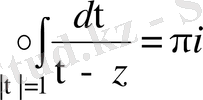 ,
,
мұндағы
 .
.
Ізделінді интеграл мына түрге енеді
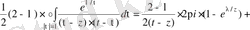
 .
.
Енді басқа интегралды есептейміз
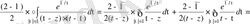
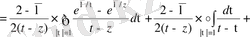
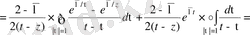
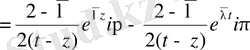 .
.
♦ Лемма 2.
 болғанда мына қатыстар орынды
болғанда мына қатыстар орынды
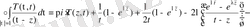
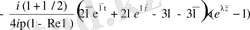
1 және 2 леммаларды ескеріп, теореманы аламыз.
▼ Теорема 1.
 ,
,
 . болсын. Онда 2. 1 теоремадан
. болсын. Онда 2. 1 теоремадан
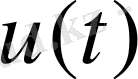 үшін сингулярлы интегралдық теңдеу Фредгольмның интегралдық теңдеуіне эквивалентті болады.
үшін сингулярлы интегралдық теңдеу Фредгольмның интегралдық теңдеуіне эквивалентті болады.
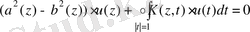
 (2. 3. 1)
(2. 3. 1)
мұндағы
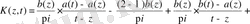
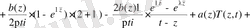
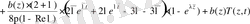 .
.
 ядро құрылымы туралы бірнеше ескерту. Алдымен
ядро құрылымы туралы бірнеше ескерту. Алдымен
 және
және
 болғанда
болғанда
 екендігін ескереміз. Екінші жағынан интегралдық теңдеудің
екендігін ескереміз. Екінші жағынан интегралдық теңдеудің
 ядросын былай жазуға болады.
ядросын былай жазуға болады.
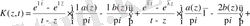
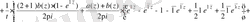
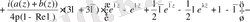

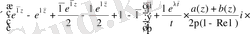
 .
.
Сонымен, ядро
 мына түрге келеді:
мына түрге келеді:
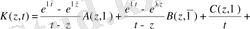

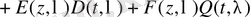
(2. 3. 2)
мұндағы Е, A, B, C, D, F, Q -t және z-ке тәуелді. Е, A, B, C, D, F, Q нақты түрін
 үшін жазылған алдынғы формулалардан қайта алуға болады.
үшін жазылған алдынғы формулалардан қайта алуға болады.
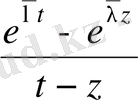 бөлшегі
бөлшегі
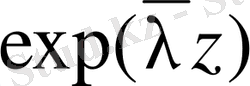 көбейткішіне дейінгі дәлдікпен (t-z) айырмасына дейін тәуелді екенін(дәрежелік қатарлар түрінде ) байқаймыз. Аналогиялы түрде алынған ұйғарым
көбейткішіне дейінгі дәлдікпен (t-z) айырмасына дейін тәуелді екенін(дәрежелік қатарлар түрінде ) байқаймыз. Аналогиялы түрде алынған ұйғарым
 болғанда
болғанда
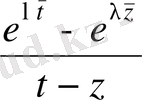 үшін
үшін
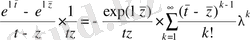 жіктеуі дұрыс.
жіктеуі дұрыс.
Соңғы (2. 3. 2) оң жағындағы үш қосылғыш сәйкесінше туындалған ядроның қосындысын береді. Осылайша (2. 3. 2) ядро туындалған бөлігінен, ал кейінгі бөлігі айырмаға тәуелді қосындыдан тұрады. Туындалған ядро [7] . монографияда көрсетілген. Айырмадан тәуелді интегралдық операторлар [8, 9] жұмыста көрсетілген. Бірақ осы жұмыстардың тікелей нәтижесін қолдану тиімсіз. [7] . монографияның IV тарауының нәтижесіне сәйкес интегралдық теңдеудің нолден өзгеше шешімі бар екендігінің қажетті және жеткілікті шарты нолге ұмтылғанадағы Фредгольм анықтауышын береді. Фредгольм анықтауышын мына формула бойынша жазылады.
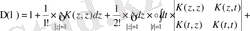
 ,
,
мұндағы
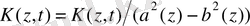 .
.
Келтірілген қатардың жинақтылығы келесі Адамар теңсіздігінен шығады. Егер D -комплекс элементтерден тұратын анықтауышы
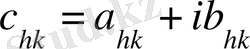 ,
,
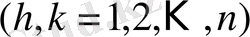 ,
,
болса, онда
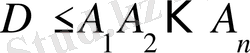 , где
, где
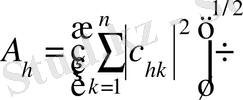 . теңсіздігі дұрыс.
. теңсіздігі дұрыс.
Шынындада λ тіркеу кезінде
 ,
,
 шарттарын қанағаттандыратын
шарттарын қанағаттандыратын
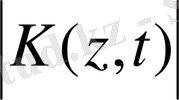 ядро модулы
ядро модулы
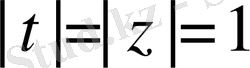 болғанда кейбір М саны үшін шектелген. Онда жоғарыдағы Адамар теңсіздігінен элементтері модулы бойынша М санынан асып кетпейтін, модулы
болғанда кейбір М саны үшін шектелген. Онда жоғарыдағы Адамар теңсіздігінен элементтері модулы бойынша М санынан асып кетпейтін, модулы
 үлкен емес n ретті анықтауыш келіп шығады. Онда Тогда
үлкен емес n ретті анықтауыш келіп шығады. Онда Тогда
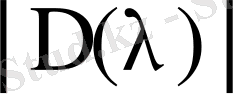 келесі жинақты қатарға мажорланады:
келесі жинақты қатарға мажорланады:
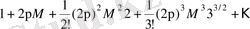 .
.
Сонымен барлық λ үшін
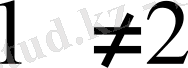 ,
,
 . шартын қанағаттандыратын Фредгольмның
. шартын қанағаттандыратын Фредгольмның
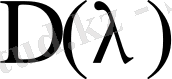 детерминанты анықталған. Бірақ,
детерминанты анықталған. Бірақ,
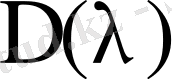 анықтауышының нолдерін табу жоғарыда келтірілген түрде жазу тиімсіз, өйткені
анықтауышының нолдерін табу жоғарыда келтірілген түрде жазу тиімсіз, өйткені
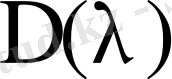 λ бойынша алынған бүтін функция болмайды және оның осы детерменанттың ең басты бөлігі ажыратылмаған
λ бойынша алынған бүтін функция болмайды және оның осы детерменанттың ең басты бөлігі ажыратылмаған
2. 4 Фредгольмның интегралдық теңдеулерін жуықтап шешу және И. А. Акбергеновтың бағалауын қолдану туралы.
Алдынғы параграфта дәл есептелінбеген Фредгольмның интегралдық теңдеулері қарастырылды. Бұл параграфта оның жуық шешімі үшін И. А. Акбергеновтың жұмысының нәтижесін қолданамыз [1, 14] . Бұл жұмыстарда 1935жылы Ленинград ғылыми-зерттеу математика, А. С. Бубнова атындағы мемлекеттік университет жанындағы механика институтында орындалған И. А. Акбергеновтың диссертациясының негізгі нәтижелері келтірілген. Бұл туралы Л. В. Канторовичпен В. И. Крыловтардың [1] монографияларында жазылған. Нақты айтқанда, И. А. Акбергенов өзінің нәтижелерін 1934 жылы Ленинград қаласында өткен екінші Бүкілодақтық математиктер съездінде баяндағаны көрсетілген [1] . И. А. Акбергеновтың [1] жұмысы библиографиялық сирек кездесетін жұмыс болғандықтан оның негізгі нәтижелерін қарастырамыз.
Бізге Фредгольмның 2-текті интегралдық теңдеуі берілсін.
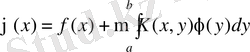 ,
,
 (2. 4. 1)
(2. 4. 1)
Берілген
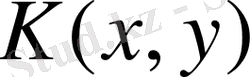 ядроны оған жақын
ядроны оған жақын
 ядросымен алмастырамыз және интегралдық теңдеуді
ядросымен алмастырамыз және интегралдық теңдеуді
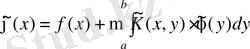 (2. 4. 2)
(2. 4. 2)
қарастырамыз
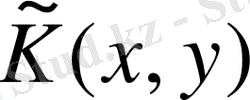 ядросының
ядросының
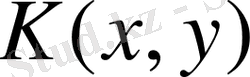 ядросына жақындығы (2. 4. 3) . қатыспен анықталған h өте аз шамамен сипаталады. μ (2. 4. 2) нің меншікті мәні болмасын.
ядросына жақындығы (2. 4. 3) . қатыспен анықталған h өте аз шамамен сипаталады. μ (2. 4. 2) нің меншікті мәні болмасын.
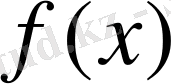 және
және
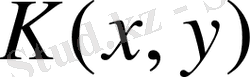 функциялары негізгі квадратта
функциялары негізгі квадратта
 ,
,
 .
.
үзіліссіз деп алынсын.
Онда келесі теорема орын алады.
▼ Теорема 1
(И. А. Акбергенов) . Егер
 ,
,
 барлық негізгі квадратта төмендегі шарттар орындалса:
барлық негізгі квадратта төмендегі шарттар орындалса:
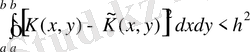 (2. 4. 3)
(2. 4. 3)
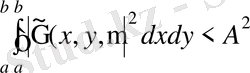 (2. 4. 4)
(2. 4. 4)
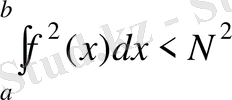 (2. 4. 5)
(2. 4. 5)
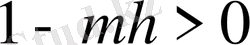 (2. 4. 6)
(2. 4. 6)
Мұндағы h және N - тұрақтылар, ал А μ-ден тәуелді
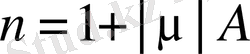 ,
,

 (2. 4. 7)
(2. 4. 7)
және
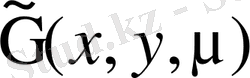 - (2. 4. 2) теңдеуінің
- (2. 4. 2) теңдеуінің
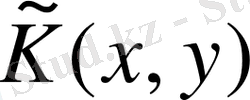 резольвентасы, онда (2. 4. 1) интегралдық теңдеудің
резольвентасы, онда (2. 4. 1) интегралдық теңдеудің
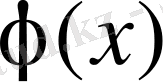 жалғыз шешімге ие болып,
жалғыз шешімге ие болып,

 (2. 4. 8)
(2. 4. 8)
орындалады.
 - (2. 4. 2) теңдеуінің шешімі.
- (2. 4. 2) теңдеуінің шешімі.
Дәлелдеу.
(2. 4. 1) теңдеуінің ядросынан
 қосып және азайтып, оны былай жазуға болады:
қосып және азайтып, оны былай жазуға болады:
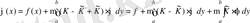 ,
,
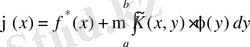
 (2. 4. 9)
(2. 4. 9)
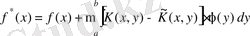 (2. 4. 10)
(2. 4. 10)
Шварц теңсіздігін пайдаланып,
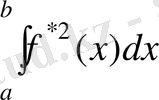 бағалаймыз.
бағалаймыз.
(2. 4. 10) қатысы бізге мынаны береді
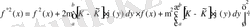 ,
,
Осыдан
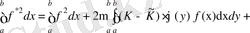
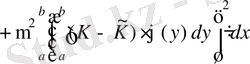 .
.
 (2. 4. 11)
(2. 4. 11)
Әрі қарай Шварц теңсіздігін екінші, үшінші қосылғыштарға қолдану соңғы теңсіздікті береді .
 ,
,
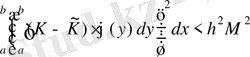 ,
,
(2. 4. 3), (2. 4. 5) -ді есепке алғанда және мұндағы

 (2. 4. 12)
(2. 4. 12)
Табылған бағалауды (2. 4. 11) теңсіздігінің оң жағына қойсақ және (2. 4. 5) ті ескеріп алатынымыз

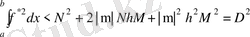 (2. 4. 13)
(2. 4. 13)
Әріқарай (2. 4. 9) интегралдық теңдеудің шешімі
 (2. 4. 14)
(2. 4. 14)
Шварц теңсіздігін пайдаланып
 бағалаймыз:
бағалаймыз:
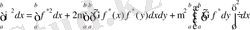
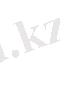 (2. 4. 15)
(2. 4. 15)
Бірақ,
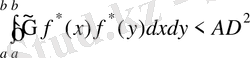 ,
,
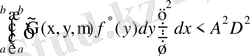
(2. 4. 4) және (2. 4. 13) қатыстары өз күшінде қалады.
Табылған бағалауды (2. 4. 15) -ке қойып және (2. 4. 13) ті ескеріп,
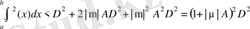 .
.
Аламыз. D -ны оның мәнімен алмастырып, (2. 4. 13) келісіп, (2. 4. 12) ескеріп, соңғы қатынасты мына түрде қайта жазамыз. согласно (2. 4. 13),
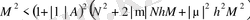
 (2. 4. 16)
(2. 4. 16)
немесе (2. 4. 7) сәйкес
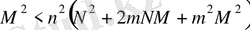 ,
,
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz