Мектепте теңдеулер мен теңдеулер жүйелерінің логикалық құрылымдарын түсіндіру әдістемесі


МАЗМҰНЫ
КІРІСПЕ . . . 3
1 МЕКТЕПТЕ ТЕҢДЕУЛЕР МЕН ТЕҢДЕУЛЕР ЖҮЙЕЛЕРІН ОҚЫТУДЫҢ ЛОГИКАЛЫҚ ҚҰРЛЫМДАРЫН ТҮСІНДІРУ 1. 1 Сызықтық теңдеу және шешудің танымдық маңызы . . . 5 1. 2 Көрсеткіштік теңдеу және көрсеткіштік теңдеулер жүйесі . . . 6 2 ТЕҢДЕУЛЕР МЕН ТЕҢДЕУЛЕР ЖҮЙЕЛЕРІНІҢ ЛОГИКАЛЫҚ ҚҰРЛЫМДАРЫН ТҮСІНДІРУ ТӘЖІРИБЕСІ 2. 1 Сызықтық теңдеулер жүйесін түсіндіру тәжірибесінен . . . 8 2. 2 Квадрат теңдеу және квадрат теңдеулер жүйесінің логикалық құрлымын түсіндіру тәжірибесінен . . . 13ҚОРЫТЫНДЫ . . . 24
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 26
КІРІСПЕ
Тақырыптың өзектілігі. Математиканы оқыту әдістемесін толық қарастыру арқылы математиканы оқытудың өзекті мәселелерін, тереңдете оқыту мәселелерін, оқыту әдістерін, жаңа технологияны меңгеру әдістерін нақты ашып түсіндіруі.
Курстық жұмыстың мақсаты. Математиканы оқыту әдістемесінің жалпы мәселелерімен таныстыру. Математиканы оқытудың әдістері, ғылыми таным әдістері, математиканың оқыту әдістемесінің маңызы, міндеттері және мақсаты, пәнаралық байланыс. Математиканы оқыту әдістемесінің өзекті мәселелерімен таныстыру. Жаңа технологиялардың қолдану мүмкіндігі, тереңдетіп оқыту мәселелері, математиканы оқытуда есептің рөлі, оқушылардың шығармашылық қабілеттерін дамыту. Жоғары сынып оқушыларына алгебралық теңдеулер мен теңсіздіктерді логикалық шешу жолдарын теориялық негізінде ашу және тиімді әдістерін күрделі есептер шығару барысында игертуге, күрделі есептер шығару барысында логикалық байланыстармен әдістерді практикалық жұмыстарда қолдана білуі арқылы біліктілігін дамытуға жағдай жасау. Оқушылардың ойлау, пікірлеу қабілеттерін арттыру, математикалық білімдерін дамыту және математика пәніне болған қызығушылығын арттыру.
Курстық жұмыстың міндеті:
-Әлемдік білім теңсіздігіне шығуда техникалық бағыттағы ғылым салаларын дамыту, әсіресе математиканың оқыту сапасын көтеру кезек күттірмейтін міндет болып табылады.
-Математиканы оқытуда оқушылардың шығармашылық қабілетін қалыптастырып, ізденімпаздыққа баулу.
-Математиканы оқытуда оқушыларды жан-жақты дамыту тұрғысынан қалыптастыру.
-Математиканы оқыту әдістерін айқындау.
-Математика сабағында жаңа технологияларды меңгеру жолдарын көрсету.
-Оқушылардың инновациялық технологияларды қолдануы.
-Сабақ уақытын тиімді пайдалану.
-Мұғалім мен оқушылардың еңбегін ғылыми тұрғыда ұйымдастыру.
Дерек көзі. Математиканы оқыту әдістемесі пәнінен әдебиеттер (Әбілқасымова А. Е., Көбесов А. К. Математиканы оқытудың теориясы мен әдістемесі. -А, 1995., Сәулебекова М. Мектеп оқушысының іс-әрекетін белсендіру-оның тұлғалық дамуының негізі. А:2011ж) және т. б. Математикалық сайттар (math. kz., itest. kz., sabaktar. kz., alphamath. kz., iqmath. kz) .
Зерттелу деңгейі. Теңдеу тақырыбының маңыздылығы және ауқымының кеңдігіне байланысты оны осы заманда үйретудің мазмұнды - әдістемелік бағыты - теңдеу және теңдеулер жүйесі. Бұл арада теңдеулер мен теңдеулер жүйелері ұғымын қалыптастыру үшін оларды шешудің жалпы және дербес әдістері, мектеп математикасының курсында санды, функционалдық бағыттар бойынша теңдеулер мен теңдеулер жүйелерін үйренудің тығыз байланыстылығы қарастырылады. Теңдеудің пайда болу облысы және теңдеу ұғымының алгебрадағы атқаратын міндетіне сәйкес мектеп математикасындағы теңдеулер мен теңдеулер жүйелерін үш бағытқа бөлеміз:
а) Қолданбалы бағыт. Теңдеулер мен олардың жүйелерін мазмұнды есептерді шешуге қолдану. Математиканың басқа ғылымда қолданылуын оқытудағы әдістер мен тәсілдер көбінесе теңдеулерге сүйенеді.
Қазіргі математиканың басқа тарауларда қолданылуы көбінесе математикалық модельдеуге байланысты. Осы ұғымды пайдаланып теңдеулер мен олардың жүйелері математикалық модельдеудегі негізгі құрал ретінде аңықталады.
б) Теңдеу мен теңдеулер жүйелерін үйренудегі теориялық - математикалық бағыт екі аспектіден тұрады:
1. аса маңызды теңдеулер және олардың жүйелерінің сыныпын оқу,
2. бір бағытқа жататын жалпыланған ұғымдармен әдістерді бүтіндей үйрену. Осы екі аспекті де мектеп математикасында аса қажет.
Теңдеулердің негізгі сыныптары жай және әрі аса маңызды математикалық модельдермен тығыз байланысты.
Курстық жұмыстың құрылымы. Курстық жұмыс кіріспеден және екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады. Көлемі-26 бет.
1 МЕКТЕПТЕ ТЕҢДЕУЛЕР МЕН ТЕҢДЕУЛЕР ЖҮЙЕЛЕРІН ОҚЫТУДЫҢ ЛОГИКАЛЫҚ ҚҰРЛЫМДАРЫН ТҮСІНДІРУ1. 1 Сызықтық теңдеу және шешудің танымдық маңызы
Сызықтық теңдеу - белгісіздері (айнымалы шамалары) 1-дәрежелі болып келетін және белгісіздердің көбейтінділері қатыспайтын теңдеу.
Мысалы,
а 1 х 1 + а 2 х 2 +…+ + а n х n = b (1)
түріндегі теңдеу n белгісізі ( аі≤0, і=1, 2, …, n ) бар сызықтық теңдеуге жатады. Егер (1) теңдеудегі а i =0 (і=2, 3, …, n ) болып, бірақ а1≤0 болса, онда ол
а 1 х = b немесе ах = b ( а 1 = а ) түріндегі бір белгісізі бар сызықтық теңдеуге айналады.
ах=в сызықтық теңдеуінің шешімі болуы үшін, біріншіден а коэффициенті нөлден өзгеше, сол сияқты, в бос мүше нөлден өзгеше болуы керек. ξ1-та баяндалған теңдеудің ғылыми теориялық мазмұнына сүйеніп, сызықтық теңдеудің қасиеттерін қиналмай тағайындауға болады.
1. Сызықтық теңдеудің 2 жағына бірдей шаманы қосқаннан теңдеу өзгермейді.
ах=в теңдеуінің екі жағына т санын қосайық, сонда ах+т=в+т. Яғни теңдеудің оң жағындағы шама т санына өзгерсе, сол жағындағы шама да дәл сондай санға өзгереді. Мысалы, айтарлық 3х=18 теңдеуі үшін т=5 десек, 3х+5=18+5.
2. Теңдеудің екі жағын бірдей шамаға кеміткеннен теңдеу өзгермейді:
ах-т=в-т
10х-7=20-7
3. Сызықтық теңдеудің екі жағын бірдей шамаға көбейткеннен теңдеу өзермейді. Теңдеудің сол жағын т бірлікке өсетін болса, оң жағы да т бірлікке өседін болса, оң жағы да т бірлікке өседі. ах=в теңдеуі үшін, т * ах=т * в Мысалы. 3*8х=3*24
4. Теңдеудің екі жағын нөлден өзгеше санға бөлгеннен, теңдеу өзгермейді. Егер т≠0 болса, онда ах=в сызықтық теңдеуі үшін ах/т=в/т орындалады.
Мысалы, 15х=200 теңдеуі т=1, 5 үшін, 15х/1, 5=200/1, 5 болады.
5. Теңдеудің бір жағындағы мүшіні теңдеудің екінші жағына қарама - қарсы таңбамен көшіруге болады. ах=в сызықтық теңдеуіндегі в санын теңдеудің сол жағына көшіру керек болсын. Ол үшін теңдеудің екі жағына -в санын қосамыз.
Теориялық мазмұны кеңінен баяндалған бағдарламалық мәселелерді оқушылардың түсіну деңгейін, олардың қырларымен сырларына ой тоқтату, күнделікті тұрмыстық мәселелерге қолдана білу қабілетін дамыту мақсатымен жеке тақырыптардың мазмұндарын танымдық жағынан дәйектеуге арналған арнайы тәжірибелерге тоқталамыз.
Мысалы. 1 піскен нан 22 теңге тұрады, яғни бір нан 22 теңге.
Бір нан сөзін х белгісізімен ауыстырайық. Өйткені, 22 теңге тұратын басқада түрліше заттар болуы мүмкін. Сонда х = 22 болады. Егер, дүкеннен бір нанның орнына 5 нан алу керек болса, онда 5х = 5* 22 яғни 5х = 110. Осы теңдеуден бастапқы теңдеуге оңай көшуге болады[1] .
Демек, соңғы теңдеуден бірінші теңдеуге көшу үшін, теңдеудің екі жағын 5- ке бөлеміз. Басқаша айтқанда, теңдеудің екі жағын бірдей санға (нөлден өзгеше) бөлгеннен теңдеу өзгермейді. Бұл сөйлем теңдеудің қасиетін анықтайды.
Демек, теңдеудің бір қасиетін анықтадық, яғни бұл сөйлем сызықтық теңдеудің өзіндік ерекшелігін сипаттайды. Сонымен, = бұдан х=22. Ал енді сызықтық теңдеудегі х- тің мәнін табу үшін, теңдеудің екі жағын белгісіз х-тің алдындағы санға бөлеміз.
Сызықтық теңдеулерге мысалдар.
- 12х = 186, 2) -3х = 24,
1) теңдеудегі х-тің мәнін табу үшін, теңдеудің екі жағын да белгісіз х-тің алдындағы сан 12-ге бөлеміз. Сонда = ; х = .
2) -3х = 24. х = = -8. Теңдеудің екі жағын да -3 санына бөлеміз.
Мысалдар. х = 22 және 5х = 110 теңдеуі берілсін. Бұған x = 22 теңдеуінің екі жағын 5 санына көбейтеміз. Теңдеудің екі жағын бірдей санға көбеткеннен, теңдеу өзгермейді.
х-15=0. Cызықтық теңдеудің екі жағына бірдей санды қосқаннан, теңдеудің мағынасы өзгермейді.
х - 15= 0 теңдеуінің екі жағына да 2 санын қосайық.
Сонда, x-15+2=0+2
Сызықтық теңдеулерді түсінудің және шешудің қыры мен сырларын меңгеру барысында олардың күнделікті тұрмыста, өмірмізде жиі қолданылатындығын оқушылар санасына орнықтырудың маңызына ерекше мән береміз.
1. 2 Көрсеткіштік теңдеу және көрсеткіштік теңдеулер жүйесі
Мысалы, егер 3
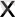 =27 болса, онда 27-ні 27=3
=27 болса, онда 27-ні 27=3
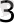 деп, былай жазамыз:3
деп, былай жазамыз:3
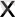 =3
=3
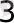 бұдан x=3. Кей жағдайда жаңадан белгісіз шама енгізу арқылы көрсеткіштік теңдеу алгебралық теңдеуге келтіріледі. Айталық, мысалы мына теңдеуді шешу керек болсын:4
бұдан x=3. Кей жағдайда жаңадан белгісіз шама енгізу арқылы көрсеткіштік теңдеу алгебралық теңдеуге келтіріледі. Айталық, мысалы мына теңдеуді шешу керек болсын:4
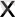 +2
+2
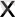 -6=0. 2
-6=0. 2
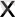 -нi y арқылы белгілейік. Сонда 4
-нi y арқылы белгілейік. Сонда 4
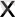 =(2
=(2
 )
)
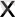 =2
=2
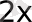 =(2
=(2
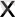 )
2
=y
)
2
=y
 болады. Сондықтан, берілген теңдеу мына квадрат теңдеуге келтіріледі:
болады. Сондықтан, берілген теңдеу мына квадрат теңдеуге келтіріледі:
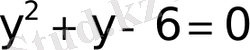 Бұдан,
Бұдан,
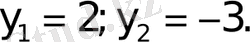 ал y=2
ал y=2
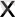 Демек, егер тек берілген теңдеудің түбірі болатын болса, онда олар не 2
Демек, егер тек берілген теңдеудің түбірі болатын болса, онда олар не 2
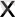 =2 Теңдеуін, не 2
=2 Теңдеуін, не 2
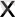 =-3 теңдеуін қанағаттандыруы тиіс. Бұл теңдеудің біріншісінің х = 1 түбірі болады, ал екіншісінің түбірі болмайды, ойткені 2
=-3 теңдеуін қанағаттандыруы тиіс. Бұл теңдеудің біріншісінің х = 1 түбірі болады, ал екіншісінің түбірі болмайды, ойткені 2
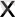 өрнегі теріс және тең болуы мүмкін емес. Сонымен шығатыны: х = 1 .
өрнегі теріс және тең болуы мүмкін емес. Сонымен шығатыны: х = 1 .
Тексеру : х = 1 болғанда, 4
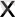 +2
+2
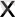 -6=4
-6=4
 +2
+2
 -6=0
-6=0
Олай болса, х = 1 - берілген теңдеудің түбірі. Жауабы: х = 1.
Мына теңдеуді шешу керек: 2
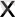 =3
=3
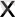 Теңдеудің екі жақ бөлігін де 3
Теңдеудің екі жақ бөлігін де 3
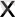 -ке бөліп
-ке бөліп
( оған бөлуге болады, өйткені х - тің кез келген мәнінде 3
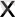 >0), табатынымыз
>0), табатынымыз
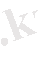
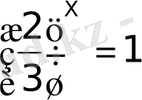 Алайда, 1=
Алайда, 1=
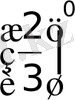 сондықтан, х = 0 болады [2] . Тексеріп қарасақ, мұның шынында да берілген теңдеудің түбірі екенін көреміз. Жауабы: х = 0
сондықтан, х = 0 болады [2] . Тексеріп қарасақ, мұның шынында да берілген теңдеудің түбірі екенін көреміз. Жауабы: х = 0
Енді көрсеткіштік теңдеулер жүйесіне есептер қарастырайық:
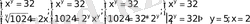
2
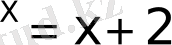 Теңдеуін графиктік тәсіл бойынша шешіп көрейік. Оң жағы корсеткіштік теңдеу, сол жағы сызықтық теңдеу. Графиктерін салайық.
Теңдеуін графиктік тәсіл бойынша шешіп көрейік. Оң жағы корсеткіштік теңдеу, сол жағы сызықтық теңдеу. Графиктерін салайық.
y=2
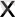 (1)
(1)
y=x+2 (2)
x=0; y=2
x=2; y=4
x
 =-1. 7; x
=-1. 7; x
 =2
=2
Тексерейiк:2
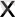 =x+2
=x+2
2
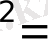 2+2-1. 7 cаны тендеудi канағаттандырмайды
2+2-1. 7 cаны тендеудi канағаттандырмайды
(Сурет 1) -де көрсетілген. Жауабы: 2.
Сурет 1. 2
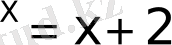 теңдеуінің графигі.
теңдеуінің графигі.
2. 1 Сызықтық теңдеулер жүйесін түсіндіру тәжірибесінен
Сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді үйренейік.
Екі белгісіз бар бірінші дәрежелі теңдеулер жүйесін графиктік тәсілмен шешкенде кездесетін мына үш түрлі жағдайды қарастырып, талдайық.
а) Екі түзі бір нүкте қиылысады. Жүйенің бір ғана шешімі болады. Мұнда салынған график бойынша түзулердің қиылысу нүктенің координаталарын тауып және х пен у-тің табылған мәндерін берілген теңдеулерге қойып, олардың екі теңдеуді де , сондықтан сол қиылысу нүктесінің координаталары берілген жүйенің шешімі болады.
ә) Екі түзу өзара дел келеді, яғни беттеседі. Бұл жүйенің көп шешімі болады.
б) Екі түзу параллель болып келсе, жүйенің ешбір шешімі болмайды.
Мысалы.
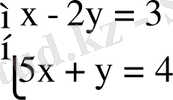 теңдеулер жүйесін берілсін.
теңдеулер жүйесін берілсін.
Ал, енді бұл есепті теңдеулер жүйесін графиктік тәсіл бойынша шешейік. Ол үшін бірінші х-2у=3 теңдеуіне мән бере отырып, у-тің мәнін табайық.
х=0, у= . х=3, у=0
Енді, екінші теңдеудегі х-ке мән бере отырып, у-ті мәнін табу керек.
х=0, у=4. х= , у=0.
Графиктерін салсақ, екі түзу А(1; -1) нүктесінде қиылысады.
Жауабы: х=1, у=0.
Есеп: Екі тік төртбұрыш берілген, біреуінің табаны 5 см, екіншісінікі 4 см, ал екеуінің аудандарының қосындысы 42 см 2 . Егер әрбір тік төртбұрыштың биіктігін өзгертпей, біріншісінің биіктігін өзгертпей, біріншісінің табанын екі еселеп, ал екіншісінің табанын 1 см арттырсақ, онда бұдан шыққан тік төртбұрыштардың аудандарының қосындысынан 33 см 2 артық болады. Әрбір тік төртбұрыштың биіктігін анықтау керек. Бұл есептің белгілеуін кесте бойынша көрсетейік. (Кесте 1) -де көрсетілген.
Кесте 1. Тіктөртбұрыш ауданы
I. Тiктөртбұрыш
II. тiктөртбұрыш
X
y
10
15
Сонда. Біздің ізделінді жүйеміз:
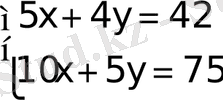 , 5x=42-4y; x=
, 5x=42-4y; x=
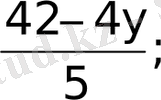
Бірінші теңдеуден х-ті у арқылы өрнектеп, екінші теңдеудегі х -тің орнына қойып, бір белгісізді сызықтық теңдеуді шешу, яғни ауыстыру тәсілін қолданып шешеміз. Сонда
10
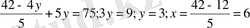 болады. Жауабы:x=6; y=3
болады. Жауабы:x=6; y=3
Мысалы.
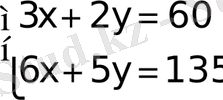 теңдеулер жүйесін шешейік. Крамер әдісі арқылы:
теңдеулер жүйесін шешейік. Крамер әдісі арқылы:
Жауабы: x 1 =10, x 2 =15.
Сызықтық теңдеулер жүйелеріКөп жағдайда есеп құрамында екі немесе одан көп заттарға (құбылыстарға) байланысты мәселелерді қатар қарастыруа тура келеді. Өкінішке орай мұндай мәселелерді сызықтық теңдеудің ауқымана симайды. Осы мақсатта сызықтық теңдеулер жүйелерін енгіземіз[3] .
x+y=6 теңдеуін де, y-x-1=0 теңдеуін де дәл (ақиқат) теңдікке айналдыратын х және у айнымалылардың мәндерінің барлық парларын табу керек болсын, яғни осы теңдеудің шешімдерінің жиындарының қиылысуын табу керек болсын.
Осыдай жағдайларда х+у=6 және у-х-1=0 теңдеулер жүйесін шешу керек. Теңдеулер жүйесін фигуралы жақшамен жазу қабылдаған. Мысалы, қарастырылып отырған теңдеулер жүйелерін былайша жазуға болады.
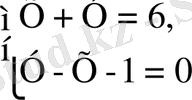 (1)
(1)
Екі айнымалысы бар теңдеулер жүйелерінің шешімі деп жүйенің әрбір теңдеуін дәл теңдікке айналдыратын айнымалылардың пар мәндерін атайды. Теңдеулер жүйесін шешу дегеніміз - оның барлық шешімдерін табу немесе оның шешімдерінің болмайтынын дәлелдеу.
- жүйені шешу үшін бір координаттық жазықтыққа х+у=6 және
у-х-1=0 теңдеулерінің графиктерін саламыз. Графиктердің қиылысу нүктелерінің әрқайсысының координаталары жүйенің бірінші теңдеуін де және сол сияқты екінші теңдеуін де қанағаттандырады, яғни теңдеулер жүйесін қанағаттандыратыны айқын (Сурет 2) .
Сурет 2. у-х-1=0 теңдеуінің графигі.
Демек, жүйенің шешімі (2, 5; 3, 5) . Теңдеулер жүйесін біз пайдаланған тәсілі графиктік тәсіл деп аталады.
Сызықтық теңдеулер жүйесінің жалпы түрі:
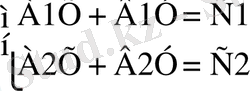
Мұндай жүйенің әр кезде де шешімі болама, ал шешімі болса, ол нешеу болады. Егер ол түзулер қиылысатын болса, онда жүйенің бір ғана шешімі болады, егер түзулер паралель болса, онда жүйенің шешімі болмайды, егер
түзулер беттесетін болса, онда шешімдері шексіз көп болады
1. Төмендегі теңдеулер жүйесі берілсін
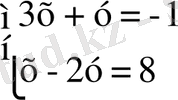
Теңдеудің әрқайсысындағы у -ті х арқылы өрнектеп, жазайық.
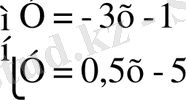
Теңдеулер жүйесінің графиктері болып табылатын түзулердің бұрыштық коэффициенттері ( -3 және 0, 5 ) әр түрлі, демек, түзулер қиылысады. Олардың қиылысу нүктелерінің координаталары осы жүйенің шешімі және бір ғана шешімі болып табылады[4] .
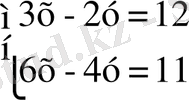 (1) теңдеулер жүйесі берілсін.
(1) теңдеулер жүйесі берілсін.
Теңдеудің әрқайсысындағы у - ті х ақылы өрнектеп, жазамыз.
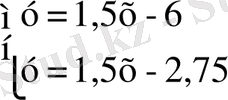 (2)
(2)
у = 1, 5х - 6 және у = 1, 5 - 2, 75 түзулерінің бұрыштық коэффиценттері бірдей, демек, бұл түзулер параллель және у = 1, 5х - 6 түзуі у осін (0; -6) нүктесінде, ал у = 1, 5х - 2, 75 түзуі (0; - 2, 75 ) нүктесін қиып өтеді, олай болса, түзулердің ортақ нүктесі жоқ (Сурет 3) . Сондықтан, (1) теңдеулер жүйесінің шешімі жоқ.
Сурет 3. у = 1, 5х - 6 және у = 1, 5 - 2, 75 функцияларының графигі.
(1) жүйесінің шешімі болмайтынына төмендегідей қарапайым пайымдау арқылы да көз жеткізуге болады.
Жүйенің бірінші теңдеуінің барлық мүшелерін 2-ге көбейтсек, 6х - 4у = 24 теңдеуі шығады, Бұл теңдеуді жүйенің екінші теңдеумен салыстырып, теңдеулердің сол жақ бөліктерінің бірдей екенін байқамыз,
сондықтан х пен у-тің бірдей бір мәнінде әр түрлі екі мән (24 және 11) қабылдай алмайды.
Сондықтан,
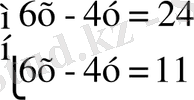 жүйесінің шешімі жоқ, демек, (1) жүйенің де шешімі жоқ.
жүйесінің шешімі жоқ, демек, (1) жүйенің де шешімі жоқ.
2. Мына жүйені қарастырайық:
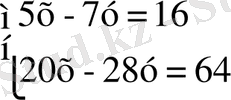
Екінші теңдеудің әрбір мүшесін 4-ке белсек, бірдей екі теңдеуден тұратын жүйе шығады.
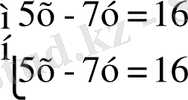
Бұл теңдеудің графиктері дәлме - дәл келеді, сол себепті графиктің кез - келген нүктесінің координаталары теңдеулер жүйесінің әрқайсысын қанағаттандырады, яғни жүйенің шешімі болады. Демек, берілген жүйенің шексіз көп шешімі бар.
Енді екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің негізгі бір тәсілі қосу тәсілімен танысайық[5] .
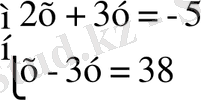
Бұл жүйенің теңдеулеріндегі у - тің коэффиценттері қарама - қарсы сандар. Теңдеулердің сол және оң бөліктерін мүшелеп қосып, бір айнымалысы бар теңдеу шығарып аламыз:
3х = 33 (1) жүйенің бір теңдеуін, мысалы біріншісін, 3х = 33 теңдеумен алмастырайық. Сонда мынадай жүйе шығады.
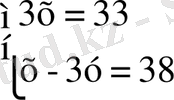 (2)
(2)
(2) жүйе (1) жүйеге мәндес болады. (2) жүйені шешейік.
3х = 33 теңдеуінен х = 11 табамыз. х - тің бұл мәнін х - 3у = 38 теңдеуіне қойсақ, онда у айнымалылы теңдеуін шығады.
11 - 3у = 38, Бұл теңдеуді шешсек:
-3у = 38 - 11; -3y = 27; y = - 9 (11; -9) пары (2) жүйенің шешімі олай болса, ол (1) жүйеніңде шешімі болады.
(1) жүйе теңдеулеріндей у-тің коэффицинттері қарама - қарсы екендігін пайдаланып, біз оның шешуін оған мәндес және бір теңдеуіне тек бір ғана айнымалы енетін (2) жүйенің шешуіне әкеп соқтырдық[6] .
2-ші мысал.
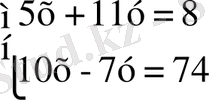 теңдеулер жүйесі берілсін.
теңдеулер жүйесі берілсін.
Егер жүйенің теңдеулерін мүшелеп қоссақ, ол ықшамдалмайды, себебі айнымалылардың ешқайсысы жойылмайды. Бірақта, егер бірінші теңдеудің барлық мүшелерін алдын - ала -2-ге көбейтсек ( ал екінші теңдеуді өзгеріссіз қалдырсақ), онда бұл екі теңдеудегі х-тің коэффицинттері қарама-қарсы сандар болады.
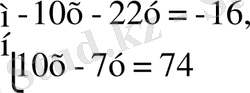
Мұны мүшелер қосудан х-тің коэффицинттері 0-ге тең болатын -29у = 58 теңдеуі шығады. Жүйенің бірінші теңдеуін -29у = 58 теңдеуі мен алмастырып, жаңа жүйені аламыз :
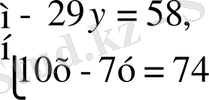 -29у = 58 теңдеуіне у = -2 мәнін табамыз.
-29у = 58 теңдеуіне у = -2 мәнін табамыз.
Жауабы: { (6; -2) }
Жалпы, екі айнымалысы бар екі сызықтық теңдеулер жүйесін қосу тәсілімен шешкенде былай істейді:
- айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болып, шығатындай етіп көбейткішті лайықтап таңдап алады да жүйенің теңдеулерін сол көбейткішке көбейтеді;
(2) жүйе теңдеулерінің сол және оң мүшелеп қосады;
(3) шыққан бір айнымалылы теңдеуді шешеді;
(4) екінші айнымалының сәйкес мәнін табады.
Енді екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің ауыстыру тәсілі деп аталатын тәсілін қарастырайық.
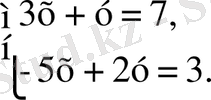 (1)
(1)
теңдеулер жүйесін қарастырайық. Бірінші теңдеудегі у-ті х арқылы өрнектейік.
у = 7 -3х. Екінші теңдеудегі у-тің орнына 7-3х өрнегін қойып, мына
жүйені шығарып аламыз:
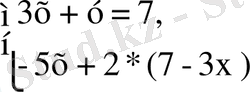 (2)
(2)
- және (2) жүйелердің шешімдері бірдей болады[7] .
- - ші жүйедегі екінші теңдеудегі тек бір ғана айнымалы енген мәнін табамыз.
У = 7 - 3х = 7 - 3 *1 =4
3. (1; 4) пары (2) жүйенің шешімі, олай болса, берілген (1) теңдеуді шешейік.
-5х + 14 - 6х = 3, -11х = -11, х= 1.
у = 7 - 3х теңдеудегі х тің орнына бір санын қойып, у тің сәйкес біз (2) жүйені шешуге желіп соқтырдық. Мұнда біз (1) және (2) жүйелердің шешімдерінің бірдей болатындығын пайдаландық.
Демек, шешімдері бірдей екі айнымалысы бар теңдеулер жүйелері мәндес деп аталады. Шешімдері болмайтын жүйелер де мәндес деп саналады. Екі айнымалысы бар екі сызықтық теңдеулер жүйесін ауыстыру тәсілімен шешкенде былай істейді:
1) қандай да бір теңдеуден бір айнымалыны екіншісі арқылы өрнектейді.
2) бұл табылған мәнді екінші теңдеудегі осы айнымалылардың орнына апарып қояды.
3) бұдан шыққан бір айнымалысы бар теңдеуді шешеді.
4) екінші айнымалының сәйкес мәнін табады.
Теңдеулер жүйесі бойынша тұрмыстағы түрліше проблемаларды шешуге болады. Оған төмендегі есептер мысал бола алады[8] .
1-мысал. Қорадағы тауықтар мен қояндар 19, ал аяқтарының саны 40,
қорада неше тауық, неше қоян бар. Тауық саны - х, қоян саны - у
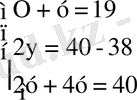 =>
=>
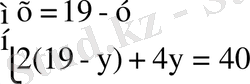 , 38 - 2y+4y=40, x=19-1=18
, 38 - 2y+4y=40, x=19-1=18
Жауабы:18 тауық, 1 қоян.
2-мысал. Бір кесе қымыз бен бір килограмм бауырсаққа 24 теңге ақша төленді. Жарты кесе қымызбен бір килограмм бауырсаққа 18 теңге ақша төленсе, бір кесе қымыз және бір килограмм бауырсақ қанша тұрады?
Бір кесе қымыз х теңге. Бір килограмм бауырсақ у теңге.
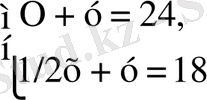 ⇒
⇒
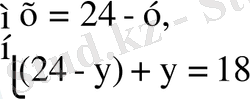 , 12 - 1/2y + =18, y - 1/2y=18-12
, 12 - 1/2y + =18, y - 1/2y=18-12
1/2y=6; y=12; x=24-12=12 Жауабы: бір кесе қымыз 12 теңге, бір килограмм бауырсақ 12 теңге тұрады.
Осы түрде өрнектелген теңдеулер жүйесі практикалық және теориялық мағыналары түрліше болып келетін сан-алуан ( мыңдаған және он мындаған) .
Сызықтық теңдеулер жүйесінің маңызы орасан зор.
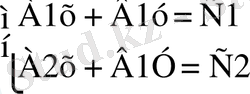 формуласындағы
формуласындағы
А, В, С, мәндерін тиянақтау арқылы тұрмыстық түрліше проблемаларды шешуге болады. Оған жоғарыда келтірілген есептер мысал бола алады.
2. 2 Квадрат теңдеу және квадрат теңдеулер жүйесінің логикалық құрлымын түсіндіру тәжірибесінен
8 сынып оқушылары “ Квадрат теңдеулер ” тақырыбын оқуға кіріскенде бірқатар білім қоры болады. Олар сызықтық теңдеулерді шеше алады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz