Орта мектепте бөлшек-рационал теңдеулер мен теңсіздіктерді шешуді оқыту әдістемесі


Мазмұны
1. 2 Теңдеулерді шешу тәсілдері . . .
1. 3 Теңсіздіктердің жалпы теориясы . . .
1. 4 Теңсіздіктерді шешу тәсілдері . . .
7
8
10
2-тарау Бөлшек-рационал теңдеулер мен теңсіздіктерді шешуге үйрету әдістемесі . . .
2. 1 Теңдеулер мен теңсіздіктерді оқыту әдістемесі . . .
12
12
Кіріспе
Жұмыстың өзектілігі. Қоғамымыздың қазіргі даму қарқыны елімізде барлық салада түбегейлі өзгерістер енгізуді қажет етеді, ал бұл өзгерістерді енгізу мамандардың кәсіби даярлығының сапасының жоғары болуын талап етуде.
Педагогикалық ғылымның басты міндеті - студенттерді кәсіби даярлау жүйесін жасау, оны жетілдіру құралдарын негіздеу.
Жоғары оқу орнында мұғалімді кәсіби даярлау жүйесі қоғамдық-саяси, арнайы, психологиялық-педагогикалық және әдістемелік дайындығын қамтиды.
«Мұғалім - әртүрлі типтегі жалпы білім беретін мектептерде оқушылармен оқу және тәрбие жұмысын жүргізетін маман». Мұғалім оқушыларды оқыту сапасына, олардың білім және тәрбие деңгейіне жауапты екендігі белгілі. Мұғалімнің жұмысы оның жеке тұлғасының негізгі сапаларының кәсіби іс-әрекетінің сипатына сай келген жағдайда ғана табысты болады. Мұғалім мектеп оқушысының негізгі құзырлылығын қалыптастыруға бағытталған оқу-тәрбие іс-әрекеттерін орындайды.
Қазақстан Республикасының 12 жылдық білім беру жүйесі бойынша құжаттарда білім беру саясатының басым бағыттарының бірі ретінде қоғам мен мемлекет, жеке тұлғаның болашақтағы қажеттіліктеріне білім берудің барлық компоненттерін сәйкестендіру және заманауи білім сапасымен қамтамасыз ету керек екендігі көрсетілген.
Мектеп математика курсында оқушылар үшін игерілуі қиын тақырыптардың бірі - бөлшек-рационал теңдеулер мен теңсіздіктер және оларды шешу. Бұл тақырыпты мұғалім жетік біліп қана қоймай, оқушыларға түсінікті, жүйелі тапсырмалар ретімен ұсынуы керек.
Осы мақсатта курстық жұмыста орта мектепте өтілетін бөлшек-рационал теңдеулер мен теңсіздіктер жан-жақты қарастырып, оны бір жүйеге келтіру мәселесін, әсіресе теориялық материалды толық меңгере отырып, берік практикалық дағды қалыптастыру мәселелерін қарастырдық.
Бөлшек-рационал теңдеулер мен теңсіздіктер теориясы оқушылардың ойлау қабілетін дамыта алатындай өз алдына ғылыми - педагогикалық маңызы бар орта мектептегі негізгі оқу материалы болып есептеледі. Ол оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Курстық жұмыстың ғылыми жаңалығы - мектеп математикасындағы бөлшек-рационал теңдеулер мен теңсіздіктерді шешу тақырыбын тереңдете оқыту мақсатында оларды шешу әдістерін көрсету, тақырыпқа қатысты материалдарды беру ретін тізбектей жүйелеу жұмыстарын, есептер топтамасын жасау.
Жұмыстың практикалық құндылығы - бөлшек-рационал теңдеулер мен теңсіздіктерді шешуге арналып дайындалған практикум тапсырмалары мен дидактикалық материалдары орта мектептің оқушыларының рационал теңдеулер мен теңсіздіктерді оқып-үйренуіне, математика пәні мұғалімдерінің оқу үдерісінде қолдануына болатындығында.
Ғылыми мәселенің қазіргі кездегі шешу жағдайында бағалауға тоқталар болсақ, мектеп бағдарламасындағы алгебра және анализ бастамалары курсының, ҰБТ-ды орта мектептерде Жоғары оқу орындарына түсуге арналған емтихан сұрақтарында бөлшек-рационал теңдеулер мен теңсіздіктер көптеп кездеседі. Осы мәселені шешу жолында бұл жұмыстың берері мол деп ойлаймыз.
Жұмыстың мақсаты - мектеп математика курсындағы «Бөлшек-рационал теңдеулер мен теңсіздіктерді шешуді оқып үйрету әдістемесі» атты тақырыпты терең меңгеру, толық қарастыру, бір жүйеге келтіру, математика сабағының танымдық деңгейін көтеру, оқушылардың математика пәніне деген қызығушылығын арттыру, дамыту.
Курстық жұмысты орындау барысында мынадай негізгі алға қойған зерттеу міндеттері қойылды:
- теңдеулердің жалпы теориясы;
- теңдеулерді шешу тәсілдері;
- теңсіздіктердің жалпы теориясы;
- теңсіздіктерді шешу тәсілдері;
- теңдеулер мен теңсіздіктерді оқыту әдістемесі;
- бөлшек-рационал теңдеулерді шешуге берілген есептерді шығару;
- бөлшек-рационал теңсіздіктерді шешуге берілген есептерді шығару.
Зерттеу нысаны: орта мектепте математиканы оқыту үдерісі.
Курстық жұмыстың теориялық және методологиялық негіздеріне Бөлшек-рационал теңдеулер мен теңсіздіктерді және оларды шешуге берілген есептерді шығарудың әдістемелік ұсыныстарын құрастыру жатады.
1 Теңдеулер мен теңсіздіктер шешудің теориялық негіздері
1. 1Теңдеулердің жалпы теориясы
Айнымалысы бар
Егер
Анықтама
Мектеп математика курсында негізінен элементар теңдеулер қарастырылады, яғни сол және оң жақтары сандар мен белгісіз функцияларға саны шектеулі элементар амалдар қолдану арқылы (қосу, алу, көбейту, бөлу, кез келген дәрежеге дәрежелеу, модуль табу, логарифмдеу) пайда болатын теңдеулер қарастырылады. Әдетте мектеп математика курсындағы элементар теңдеулер рационал, иррационал және трасценденттік деп бірнеше бөлікке бөлінді.
Рационал теңдеулерге бүтін рационал және бөлшекті-рационал теңдеулер жатады.
Анықтама
Анықтама
Енді осы анықтамаларға мысалдар келтірейік.
а)
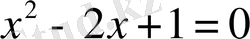 ,
,
б)
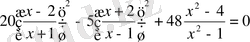 Equation. 3,
Equation. 3,
Анықтама Теңдеудің анықталу облысы деп немесе берілген теңдеудің мүмкін мәндерінің облысы деп, осы теңдеудің екі жағының да мағынасы болатын, теңдеуге еніп тұрған аргументтердің барлық мәндерінің жиынын айтады. Белгіленуі:
Осы анықтамадан көрініп тұрғанындай, теңдеудің әрбір түбірі оның анықталу облысына тиісті, бірақ теңдеудің анықталу облысына жататын кез келген сан оның түбірі бола бермейді. Ал теңдеудің мүмкін мәндерінің облысына жатпайтын сан, оның түбірі бола алмайды. Яғни, санның теңдеудің анықталу облысына тиісті болуы қажетті шарт, бірақ ол жеткілікті шарт емес. Мысалдар келтірейік.
1.
теңдеуінің анықталу облысы
Сонымен:
Мәндес теңдеулер ұғымы.
Анықтама Егер екі теңдеудің біреуінің әрбір түбірі екіншісінің де түбірі болса және керісінше болса, онда бұл теңдеулерді мәндес теңдеулер (эквивалентті теңдеулер) деп атайды.
Мәндес (бара - бар) көшуді “
 ” логикалық мәндестік (эквиваленттілік) белгісі.
” логикалық мәндестік (эквиваленттілік) белгісі.
Екі теңдеудің мәндестігі белгілі бір облыста қарастырылады. Екі теңдеу қандай-да бір облыста мәндес болып, басқа бір облыста мәндес болмауы мүмкін.
Енді мәндес теңдеулердің кейбір қасиеттерін қарастырып өтейік.
Теорема-1 (Рефлексивтілік қасиет) . Егер екі теңдеудің біреуі екіншісіне мәндес болса, онда екіншісіде біріншісіне мәндес болады.
Теорема-2 (Транзитивтілік қасиет) . Егер үш теңдеудің біріншісі екіншісіне мәндес болса, ал екіншісі үшіншісіне мәндес болса, онда біріншісі үшіншісіне мәндес болады.
Теорема-3 Егер
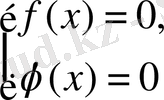 теңдеулер жиынтығына мәндес болады.
теңдеулер жиынтығына мәндес болады.
Теорема-4 Егер
Теорема-5 Егер
Теорема-6
Теорема-7
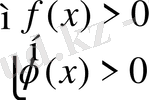
теңсіздіктер жүйесін қанағаттандыратын барлық
теңдеуіне мәндес [1], [2], [3] .
1. 2 Теңдеулерді шешу тәсілдері
Анықтама
Анықтама
Жалпы жағдайда
Теңдеулерді шешудің көбейткіштерге жіктеу әдісі
Көбейткіштерге жіктеу әдісі мынаған негізделген: егер
теңдеулер жиынтығының да шешімі болады.
Теңдеулерді шешудің жаңа айнымалы енгізу әдісі
f(x) = 0 теңдеуін р(g(x) ) = 0 түріндегі теңдеуге түрлендіру мүмкін болса, онда u = g(x) айнымалысын енгізіп, p(u) = 0 теңдеуін шешеді . Егер p(u) = 0 теңдеуінің түбірлері
Жаңа айнымалыны енгізу теңдеуді шешуді әлдеқайда оңайлатады. Сондықтан теңдеуді шешу үшін жаңа айнымалыны дұрыс таңдай алу, есепті неғұрлым оңай шығаруға алып келеді.
Оқушыларды теңдеуді шешу үшін оны бірден түрлендіруге асықпастан, қандай жаңа айнымалы енгізсек есептің шығарылуы оңайлауы мүмкін деп ойлануға үйрету керек. Егер теңдеудің шартынан жаңа айнымалыны енгізу бірден белгілі бола қоймаса, онда қандай түрлендірулер жасасақ жаңа айнымалыны енгізу мүмкіндігі бар деп ойлану керек.
Сондықтан жаңа айнымалыны енгізу бірден теңдеуді шешуге кірісу кезінде, немесе біршама түрлендірулерден кейін көрінуі де мүмкін, кейде бір емес, екі жаңа айнымалы енгізуге тура келетін жағдайлар да кездеседі.
Теңдеулерді шешудің функционалды-грфиктік әдісі
1. y=
2. Графиктер қиылысса, қиылысу нүктесін табады.
Графиктердің қиылысу нүктесінің абссицасы теңдеудің түбірі болады.
y=
Бұл әдіс теңдеудің түбірлерінің санын және теңдеудің түбірлерін дәл немесе жуықтап анықтауға мүмкіндік береді.
Егер х аралығында y=
1. 3 Теңсіздіктердің жалпы теориясы
Теңсіздіктер туралы жалпы түсінік.
Заттарды санауға байланысты және әр түрлі шамаларды салыстыру қажеттілігінен теңдік ұғымымен қатар «артық» және «кем» ұғымы шыққан. Салыстырылатын екі санның арасына > (үлкен), < (кіші) немесе = (тең) белгілерінің біреуі қойылатынын білеміз.
> және < белгілері - қарама-қарсы теңсіздік белгілері. > мен > және < мен < белгілері - бірдей теңсіздік белгілері.
Мысалы, 6>0 және -1<0 қарама-қарсы теңсіздік белгілері бар санды тенсіздіктер. 2>0 және 9>0 бірдей теңсіздік белгілері бар санды теңсіздіктер.
Теңсіздік белгісінің сол жағындағы өрнек теңсіздіктің сол жақ бөлігі деп аталса, оң жағындағы өрнек теңсіздіктің оң жақ бөлігі деп аталады.
Теңсіздіктің сол жақ бөлігіндегі және оң жак бөлігіндегі қосылғыштар оның мүшелері деп аталады.
Мысалы, 7, 5+3>5, 1+2 теңсіздігіндегі 7, 5+3 - теңсіздіктің сол жақ бөлігі, ал 5, 1+2 - теңсіздіктің оң жақ бөлігі; 7, 5; 3; 5, 1 және 2 - теңсіздіктің мүшелері.
Теңсіздік мағынасына қарай тура теңсіздік және тура емес теңсіздік болып бөлінеді.
Мысалы: 7, 5>7, 3 - тура теңсіздік; 6, 2<4 - тура емес теңсіздік.
Есептеулерде тура теңсіздіктер қолданылады, сондықтан «теңсіздік» сөзін ғана пайдаланамыз.
Санды теңсіздікте сандарды әріппен белгілесек, теңсіздік a>b; c<d түрінде жазылады. Мұндағы а, b, с және d - кез келген сандар (санды өрнектер) .
Сандарды салыстыруда үш түрлі жағдай кездеседі.
Олар: 1) а>b; 2) а<b; 3) а=b.
Берілген екі санды (санды өрнекті) салыстырғанда аталған үш жағдайдың біреуі ғана орын алады.
Анықтама Теңсіздік деп өзара бір-бірімен > (үлкен) немесе < (кіші) белгілерімен жалғасқан екі аналитикалық өрнекті айтады.
Анықтама Егер а-b айырымы, мұндағы
Анықтама Егер а-b айырымы, мұндағы
Анықтама а саны a>b немесе a<b теңсіздігінің сол жақ бөлігі, b саны оң жақ бөлігі деп аталады.
Анықтама a>b және c>d немесе a<b және c<d екі теңсіздіктері бірдей мағыналы теңсіздіктер деп аталады.
Анықтама a>b және c<d немесе a<b және c>d екі теңсіздіктері қарама-қарсы мағыналы теңсіздіктер деп аталады.
Анықтама > немесе < белгілерімен жалғасқан теңсіздіктерді қатаң теңсіздіктер, ал
Анықтама Бір белгісізді теңсіздік деп
Анықтама
Анықтама
Анықтама Теңсіздік белгісіздерінің барлық мүмкін мәндер жиынын оның анықталу облысы деп атайды. Белгіленуі:
Мәндес теңсіздіктер жөніндегі негізгі тұжырымдар.
Анықтама Егер
Теорема-1
Теорема-2
Теорема-3
Теорема-4 Егер
Теорема-5 Егер
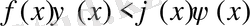 теңсіздігі шығады.
теңсіздігі шығады.
Теорема-6
Теорема-7
 және
және
Теорема-8
Теорема-9 Егер А жиынында
Теорема-10
Теорема-11
Теорема-12
Теорема-13 (0; 1) аралығындағы кез келген а үшін және А жиынында оң
1. 4 Теңсіздіктерді шешу тәсілдері
Теңсіздіктерді шешуде түрлі тәсілдерді қолданып шешу тәсілі нәтиженің көрінісінде көркемдей түседі, әсіресе оқушылардың логикалық ойлау қабілетінің, ойлау мәдениетінің қалыптасып дами түсуіне ықпал етуі анық.
Берілген есептердің әрқайсысын бірнеше тәсілдермен шығара алған оқушы есептерді шешудің ең тиімді жолын оңай тауып, әсемдік көріністі көре алады.
Теңсіздіктерді шешуде келесі тәсілдер қолданылады:
1) Теңсіздікті шешудің аналитикалық тәсілі;
2) Теңсіздікті шешудің графиктік тәсілі;
3) Теңсіздікті шешудің интервалдар әдісі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz