Гамильтон-Якоби әдісі негізінде екі қозғалмайтын нүктенің бейстационарлық моделін интегралдау


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:
КІРІСПЕ
Екі қозғалмайтын нүктенің модельдік есебі тақырыбына ұқсас жақын арада жарық көрген бірнеше жұмыстар белгілі, оларда гравитациялық өрістегі материалдық нүкте қозғалысының есептері қарастырылған. Жердің гравитациялық өрісіне жуық, мұндай қойылған есептер қозғалыстың дифференциялдық теңдеулерінің шешімдері болуы мүмкін [1, 2, 5, 29-35] .
Жұмыстың негізгі нәтижелері төмендегі конференцияларда мақала ретінде дайындалып, талқыланды:
1. Усовские чтения «Методология и методика формирования научных понятий у учащихся школ и студентов вузов» тақырыындағы ХХ халықаралық ғылыми - тәжіриелік конференцияның материалдары, І бөлім. Челяинск, 4-5 сәуір, 2013ж.
2. Төлегенов оқулары «Қазақстанның білім беру жүйесін дамытудағы инновациялық бағыттар» тақырыбындағы республикалық ғылыми-тәжірибелік конференциясының І бөлімі. Ы. Алтынсарин атындағы АрқМПИ, Арқалық, 12 сәуір, 2013ж.
3. «Шоқан тағылымы - 17» Халықаралық ғылыми - практикалық конференция бағдарламасы Көкшетау, 25-26 сәуір, 2013ж.
4. «ХІІ - Халықаралық Байқоңыр оқулары» ғылыми - практикалық конференция бағдарламасы Жезқазған, 15-16 қараша, 2013 ж.
5. Төлегенов оқулары «Заманауи білім беру жүйесі: тәжірибеден - болашаққа» тақырыбындағы республикалық ғылыми - тәжірибелік конференцияның материалдары. Ы. Алтынсарин атындағы АрқМПИ, Арқалық, 11 сәуір, 2014ж.
Тағайындалған жұмыста алынған нәтижелер зерттеу зерзаты - «Екі қозғалмайтын нүктенің модельдік есебі» мәселесін әрі қарай дамыту іргетасын қалайды.
Дипломдық жұмыстың толық көлемі 63 бет. Ол жоспары, кіріспе, үш тараудан тұратын негізгі бөлім, қорытынды, пайдаланылған 34 әдебиеттен тұрады.
Жұмыстың өзектілігі. Гамильтон-Якоби әдісі канондық теңдеулердің интегралдауының жемісті және икемді әдістерінің бірі болып табылады. Осы мақсатта Гамильтон-Якоби теңдеуі құрастырылғаннан кейін оның табылған толық интегралынан бастапқы есептері шығарылуы мүмкін. Гамильтон-Якоби теңдеуінің толық инегралын табудың жалпы әдісі жоқ, бірақ Гамильтон-Якоби теңдеуінің жеке интегралдау әдістері бар. Сондықтан Гамильтон-Якоби теңдеуінің интегралдау мәселесі классикалық механикада өзекті болып қала береді.
Жұмыстың ғылыми жаңалықтары:
- жұмыста Гамильтон - Якобидің интегралданған бейстационарлы теңдеуінің дара шешімдері анықталған;
- екі қозғалмайтын нүктелердің тартылуы яғни біз білетіндей эллипстік квадратта интегралдануы;
- орталық сфералық емес дененің тартылуының әсерінен материалдық нүкте қозғалыс есептеріне жуық есептерінің шешімдері үлкен планеталар спутниктерінің қозғалыс теориясында бұл есеп маңызды рөл атқарады;
- Жердің күштік функцияларының кейбір сыртқы нүктелерде (геоцентрлік және экваторлық) бөлінуі;
Жұмыстың практикалық маңызы. Дипломдық жұмыстағы табылған жаңа нәтижелердің теориялық маңызы - оларды басқа да екі дене мәселесінің әртүрлі күрделі қойылымдарын зерттеуде алғашқы жуық қозғалыс ретінде қарастыруға болады. Ал, ғылыми практикалық маңызы - табылған жаңа шешімдерді аспан денелерінің жасанды және табиғи серігінің динамикалық эволюциясындағы екінші дененің гравитациялық әсерін есептеуде пайдалануға болады.
Жұмыстың мақсаты. Теориялық механикаға қатысы бар массасы айнымалы денелердің есептерін интегралданған Гамильтон - Якобидің бейстационарлық теңдеулері арқылы шешу. Екі қозғалмайтын нүктенің жинақталған есептерінің күштік функциясының өзгешеліктерін зерттеу.
Зерттеу объектісінің теориялық және әдіснамалық негіздері. Дипломдық жұмыста Гамильтон-Якоби теңдеуінің бейстационарлық интегралдау жағдайы және динамикалық жүйенің бір класы үшін Гамильтон-Якоби теңдеуі қарастырылады. Денелерді материялық нүкте деп қабылдап олардың өзара Ньютон заңымен әсерлесетіндігі салыстырмалы қозғалысы қарастырылады. Жазық беттегі қозғалмайтын екі дененің орта есебі мәселесін қарастырамыз. Ал жұмыста осы мәселелерде есептерді құру және қозғалыстың бейстационарлық теңдеулері көрсетілген. Гамильтондық жүйеде толық интегралын көрсетуге болатын бір класс ұсынады. Бұны бейстационарлық жүйелерге қарай В. Г. Деминнің нәтижелерін жалпылайтын және Г. Дарбу интегралдау жағдайларын енгізетін келесі теорема дәлелденеді [3] .
Т е о р е м а . Нөлге тең емес
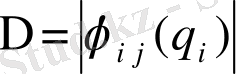 анықтауыш үшін
анықтауыш үшін
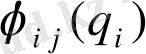 ,
,
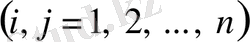 n
2
кез келген функциясы, және (2n+1) кез келген функция
n
2
кез келген функциясы, және (2n+1) кез келген функция
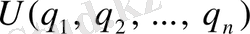 ,
,
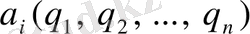 ,
,
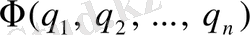 координаттарын және
координаттарын және
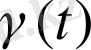 уақытты жалпылайтын болсын.
уақытты жалпылайтын болсын.
- екі дене квадратурасы астрономия есептері болашақта қолданылуы мүмкін. Ал, қазірше математика немесе теориялық механика жағынан қолданылады.
- екі қозғалмайтын нүктелердің бейстационарлық есебінің бір нұсқасы базасында қосымша күш болғандағы, серіктің жылдамдығы пропорционал және массаның өзгеруіндегі салыстырмалы жылдамдығы болған кездегі Жердің жасанды серігінің қозғалысы туралы есепті қарастырамыз. Серіктің ұйытқу қозғалысы элементтерін оскулирлеу үшін дифференциалды теңдеуді шығарамыз. Алынған нәтижелер Жердің жасанды серігінің орбиталық қозғалысында гравитациялық айнымалы эффекті талдау кезінде, сонымен қатар, массасы айнымалы аспан денесі механикасы есебінде одан әрі пайдалану үшін қолданыла алады.
1 БЕЙСТАЦИОНАРЛЫҚ МЕХАНИКА ЕСЕБІНДЕГІ ГАМИЛЬТОН-ЯКОБИ ӘДІСІ
1. 1 Гамильтон-Якоби теңдеуінің дифференциалдық жүйесі
Гамильтон - Якоби теңдеуінің интегралдау механикада өзекті мәселелердің бірі болу үстінде, себебі Гамильтон-Якоби әдісі канондық теңдеулердің интегралдауының жемісті және икемді әдістерінің бірі болып табылады. Осы мақсатта Гамильтон-Якоби теңдеуі құрастырылған, кейін оның табылған толық интегралынан бастапқы есептің шығарылуы келтірілген. Гамильтон-Якоби теңдеуінің толық инегралын табудың жалпы әдісі жоқ, бірақ Гамильтон-Якоби теңдеуінің жеке интегралдау әдістері бар.
Гамильтон зерттеуі 1834 жылы бастау алды, ал ол идеяны кейін Якоби 1936 жылы дамытты. Гамильтон-Якоби интегралдау теңдеуіне апаратын, канондық жүйенің теңдеуін интегралдау әдісі осылай пайда болды. 1849 жылы Лиувилль Гамильтон - Якоби теңдеуін айнымалы бөліну әдісімен интегралдаудың жеткілікті жалпы шарт ойлап тапты. 1881 жылы Штеккель осы теңдеудің біршама жалпы интегралдау шартын келтірді.
1887 жылы Моррера (H) Гамильтон функциясы үшін екі еркін дәрежесі бар, (H) функциясына салыстырмалы екінші тәртіпте жеке туындыдағы дифференциалды теңдеуімен көрсетілетін және (H) функциясын қанағаттандыруда осы шартқа Гамильтон-Якоби теңдеуінің сәйкес толық интеграл жағдайында айнымалыны бөлудің толық интеграл шартын орнататын механикалық жүйені тапты.
1904 жылы Леви-Чивита n саны еркіндік дәрежесі склеромды механикалық жүйенің еркін жағдайына Моррера шартын қорытындылады, ал 1944 жылы Моррера-Леви-Чивита шарты Форбаттың реономдық жүйесі жағдайында қорытындыланды.
Бұл шарттарды келесі жеке туындыда дифференциалды теңдеу жүйесінде көрсетуге болады:
(1. 1)
(1. 2)
мұндағы Н - Гамильтон функциясы,
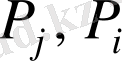 - жалпылама импульс,
- жалпылама импульс,
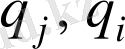 - жалпылама координаттар,
- жалпылама координаттар,
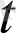 - уақыт.
- уақыт.
Егер (
 ) сөзсіз уақытқа тәуелді болмаса, онда (1. 2) шарт тепе-тең қанағаттандырылады, және Леви-Чивита шығарған шарт болады [1-2] .
) сөзсіз уақытқа тәуелді болмаса, онда (1. 2) шарт тепе-тең қанағаттандырылады, және Леви-Чивита шығарған шарт болады [1-2] .
Егер Гамильтон функциясында
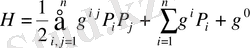 (1. 3)
(1. 3)
(1. 1) және (1. 2) шартына алмастырса, онда олар
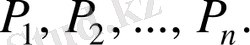 импульсі жөніндегі үшінші және төртінші дәрежеге сәйкес полиномаға өтеді.
импульсі жөніндегі үшінші және төртінші дәрежеге сәйкес полиномаға өтеді.
Сонда
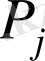 туындысында тәуелсіз тұрақтылық, онда (1. 1) және (1. 2) шарттары осы полиномдардың коэффиценттері нөлге тең келгенде және
туындысында тәуелсіз тұрақтылық, онда (1. 1) және (1. 2) шарттары осы полиномдардың коэффиценттері нөлге тең келгенде және
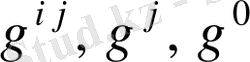 функциясы, олардың бірінші және екінші реттегі жеке туындысы болып келген жағдайда ғана қанағаттандырылады.
функциясы, олардың бірінші және екінші реттегі жеке туындысы болып келген жағдайда ғана қанағаттандырылады.
Сөйтіп, Моррера есебі
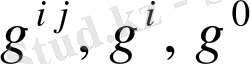 функциясы жөніндегі екінші реттік жеке туындыда дифференциалды теңдеудің интегралдау жүйесі есебіне апарады.
функциясы жөніндегі екінші реттік жеке туындыда дифференциалды теңдеудің интегралдау жүйесі есебіне апарады.
1963 жылы М. С. Яров-Яровой реономды механикалық жүйеде Гамильтон функциясының толық түрін, айнымалы бөліну әдісімен табуға болатын Гамильтон-Якоби теңдеуінің толық интегралын орнатты және Гамильтон-Якоби теңдеуіне тиісті толық интегралын құрды [3-5] .
Механикалық жүйенің біршама кең класын көрсетті. М. С. Яров-Яровоймен алынған нәтижелер Бургатти склерономдық жүйесі үшін алынған интегралдау жағдайының туралығын дәлелдеді [6, 7] .
М. С. Яров-Яровой нәтижелерінен, сондай-ақ, Гамильтон-Якоби теңдеуінің толық интервалы айнымалыны бөлу әдісімен тек салыстырмалы импульстің бірінші және екінші ретті болып табылатын механикалық жүйенің бастапқы интегралы болған жағдайда ғана табылуы мүмкіндігі қорытындыланды. Осы себеппен айнымалы бөлінулер әдісімен шешуге болатын сан есебі бойынша Гамильтон-Якоби теңдеуі интегралын толық құру мәселесі бұрынғыша ашық күйінде қалды.
Гамильтон-Якоби әдісі канондық теңдеулер жүйесін интегралдаудың біршама қуатты әдістердің бірі болып табылады және қазіргі уақытта голономдық жүйе механикасы есебін шешуде Гамильтон-Якоби әдісін қолдану арқылы көптеген маңызды жетістіктерге қол жеткізілді.
Гамильтон-Якоби әдісімен интегралдау мәселесі аспан механикасында көп орын алатынын және де қазіргі кезде кең дамығанын айта кету керек [8-14] . Гамильтон-Якоби әдісі бейстационарлы жүйені зерттеуді біршама дәрежеде жеңілдетуімен қатар, соңғы кездері оған зор қызығушылық туып отыр. Сонымен бірге, Гамильтон-Якоби теңдеуін интегралдаудың жаңа жағдайын орнататын А. А. Беков пен Т. Б. Омаровтың зерттеу нәтижелері де үлкен қызығушылық тудырды [15-20] . Оларда В. Г. Деминнің, Лиувилль және Штеккельдің интегралдау жағдайы бар, сонымен бірге қарастырылатын Гамильтон-Якоби теңдеуін қолдана отырып, М. С. Яров-Яровойдың нәтижелерін қорытындылайды [21-29]
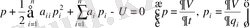 (1. 4)
(1. 4)
Мұндағы,
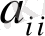 -
-
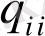 координат функциясы,
координат функциясы,
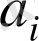 -
-
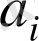 координат функциясы,
координат функциясы,
 - күш функциясы,
- күш функциясы,
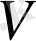 - Гамильтон-Якоби теңдеуінің толық интегралы.
- Гамильтон-Якоби теңдеуінің толық интегралы.
1. 2 Интегралдаудағы Гамильтон-Якоби теңдеуінің қолданылуы
Соңғы уақыттары астрономия мен космологияның дамуына байланысты аспан механикасы бейстационарлы моделдік есебін зерттеуге үлкен назар аударылып отыр. Сондай-ақ осы бейстационарлы жүйені сипаттайтын, қозғалыстың дифференциалды теңдеуін интегралдау мәселесі маңызды қызығушылық тудырды.
Бейстационарлы динамикалық жүйелер үшін қосымша ретінде келесі теоремаларды қарастырамыз.
Т е о р е м а . Егер Гамильтон функциясы
 (1. 5)
(1. 5)
формуламен анықталса, онда
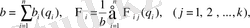 (1. 6)
(1. 6)
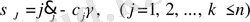 , (1. 7)
, (1. 7)
болады.
мұндағы,
 - еркін үзіліссіз функциялар,
- еркін үзіліссіз функциялар,
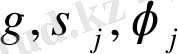 - уақыттың үзіліссіз функциялары,
- уақыттың үзіліссіз функциялары,
 - еркін тұрақты,
- еркін тұрақты,
онда Гамильтон-Якоби теңдеуі толық интегралды игеріледі
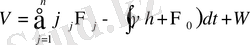 (1. 8)
(1. 8)
мұнда
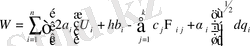 , (1. 9)
, (1. 9)
мұндағы
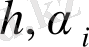 - еркін тұрақты, және де
- еркін тұрақты, және де
 . (1. 10)
. (1. 10)
Д ә л е л д е у. Тиісті теңдеу үшін
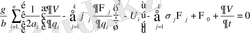
шешімі (1. 9) түрінде, мұндағы
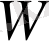 - белгісіз функция
- белгісіз функция
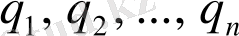 .
.
(1. 7), (1. 8) күште
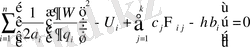 ,
,
шартын қанағаттандыратын
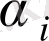 (1. 10) шешімі бар теңдеу аламыз.
(1. 10) шешімі бар теңдеу аламыз.
Енді тек шартты тексеру ғана қалады
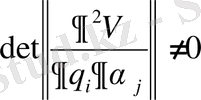 .
.
бар
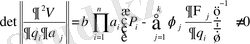 ,
,
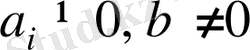 . Шарты бойынша
. Шарты бойынша
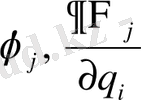 функциясы секілді үзіліссіз Теорема дәлелденді.
функциясы секілді үзіліссіз Теорема дәлелденді.
Т е р г е у . 1
0
. Егер (1. 8)
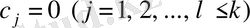 , яғни
, яғни
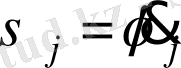 , а
, а
 - еркін үзіліссіз функция болса, онда (1. 10) формуласында j бойынша жинақтау
- еркін үзіліссіз функция болса, онда (1. 10) формуласында j бойынша жинақтау
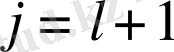 ден
ден
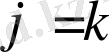 ге дейін жүреді.
ге дейін жүреді.
2
0
. Егер (1. 8)
 болса, онда А. А. Бековтың интегралдау жағдайын аламыз [10] .
болса, онда А. А. Бековтың интегралдау жағдайын аламыз [10] .
3
0
. Егер
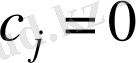 және
және
 кезінде А. А. Беков пен Т. Б. Омаровтың интегралдау жағдайын аламыз [27] .
кезінде А. А. Беков пен Т. Б. Омаровтың интегралдау жағдайын аламыз [27] .
4
0
. (1. 6) жорамалдасақ, барлық
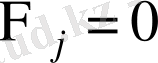 М. С. Яров-Яровойдың интегралдау жағдайын аламыз [14] .
М. С. Яров-Яровойдың интегралдау жағдайын аламыз [14] .
Егер
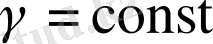 және
және
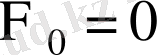 болса, онда Лиувиллдің теоремасына келеміз [25] .
болса, онда Лиувиллдің теоремасына келеміз [25] .
1. 3 Гамильтон-Якоби теңдеуінің бейстационарлық интегралдау жағдайы
Бейстационарлық жүйелерге қарай В. Г. Деминнің нәтижелерін жалпылайтын және Г. Дарбу интегралдау жағдайларын енгізетін теорема дәлелдейді. Ол Гамильтондық жүйеде толық интегралын көрсетуге болатын бір класс ұсынады [23-25] .
Т е о р е м а . Нөлге тең емес
 анықтауыш үшін
анықтауыш үшін
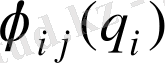 ,
,
 n
2
кез келген функциясы, және (2n+1) кез келген функция
n
2
кез келген функциясы, және (2n+1) кез келген функция
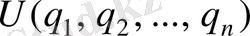 ,
,
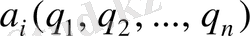 ,
,
 координаттарын және
координаттарын және
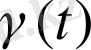 уақытты жалпылайтын болсын.
уақытты жалпылайтын болсын.
Онда, гамельтониан бейстационарлық жүйесі мына формуламен анықталады:
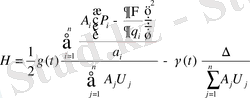 , (1. 11)
, (1. 11)
Мұнда
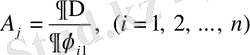 , (1. 12)
, (1. 12)
Онда Гамильтон-Якоби теңдеуінің тиісті интегралы
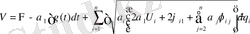 , (1. 13)
, (1. 13)
болады.
мұндағы
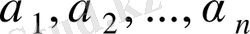 - кез келген тұрақты.
- кез келген тұрақты.
Д ә л е л д е у . Кез келген теңдеуді шешу
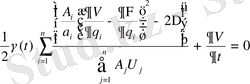 (1. 14)
(1. 14)
түрінде қарастырамыз
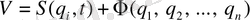 (1. 15)
(1. 15)
онда
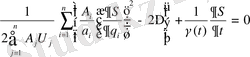 . (1. 16)
. (1. 16)
шығады.
S функциясын түрінде
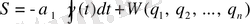 (1. 17)
(1. 17)
алып, өзгертеміз (1. 16) :
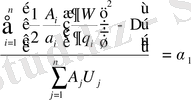 (1. 18)
(1. 18)
Енді, ұсына отырып
 (1. 19)
(1. 19)
және (1. 12) өрнегі (1. 18) теңдеуінде, болатынын
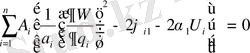 . (1. 20)
. (1. 20)
W сома түрінде ұсынылған болсын
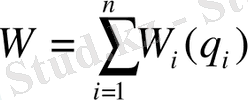 , (1. 21)
, (1. 21)
онда (1. 20) теңдеуі
 . (1. 22)
. (1. 22)
қанағаттандырады .
Шындығында, (1. 20) сол бөлігіне (1. 22) ұсына отырып,
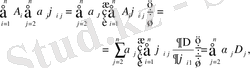 (1. 23)
(1. 23)
аламыз.
Мұнда
 .
.
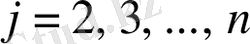 үшін
үшін
 белгілі анықтауыш қасиет күшінде екенін аңғарамыз.
белгілі анықтауыш қасиет күшінде екенін аңғарамыз.
Әрі қарай, (1. 22) интегралдау арқылы және (1. 21), (1. 17) мен (1. 15) формулаларын ескере отырып, (1. 11) теңдеуінің (1. 13) толық инегралын табамыз, сонымен теореманы дәлелдеуді аяқтаймыз.
Егер (1. 11) гамильтонианына
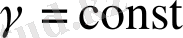 салсақ, онда В. Г. Деминнің теоремасын аламыз [22] . Егер
салсақ, онда В. Г. Деминнің теоремасын аламыз [22] . Егер
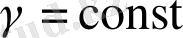 шартына қосымша ретінде
шартына қосымша ретінде
 қойсақ, онда Г. Дарбудың интегралдау жағдайына келеміз [19] .
қойсақ, онда Г. Дарбудың интегралдау жағдайына келеміз [19] .
1. 4 Динамикалық жүйенің бір класы үшін Гамильтон-Якоби теңдеуі
Динамика жүйесінің тағы бір классын белгілеуге мүмкіндік беретін Гамильтон - Якоби теңдеуінің толық интегралын көрсететін теореманы дәлелдейік.
Бұл теорема М. С. Яров-Яровтың нәтижесін жалпылайды және бейстационарлы жүйеге сәйкес В. Г. Деминнің интегралдау жағдайын енгізеді [17, 21] .
Т е о р е м а .
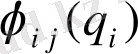 ,
,
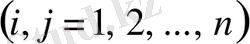 еркін функция n
2
болсын делік, яғни бірдей нөлге тепе-тең емес
еркін функция n
2
болсын делік, яғни бірдей нөлге тепе-тең емес
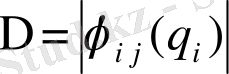 анықтауыш үшін,
анықтауыш үшін,
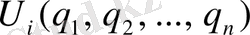 ,
,
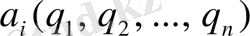 ,
,
 жалпылама координаттың және
жалпылама координаттың және
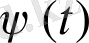 ,
,
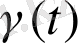 уақыттың n(2n+1) еркін функциясы.
уақыттың n(2n+1) еркін функциясы.
Онда, егер гамильтиониан бейстационарлы жүйесі
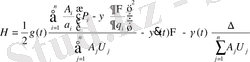 (1. 24)
(1. 24)
функциясымен анықталады.
Мұндағы
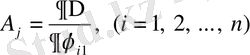 , (1. 25)
, (1. 25)
Немесе Гамтльтон-Якоби теңдеуінің сәйкестігі үшін толық инеграл мына түрде болады.
 , (1. 26)
, (1. 26)
Мұндағы
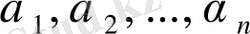 - еркін тұрақты.
- еркін тұрақты.
Д ә л е л д е н д і. Сәйкесінше теңдеуді шешімі
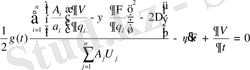 (1. 27)
(1. 27)
түрінде іздейміз
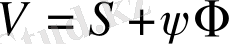 . (1. 28)
. (1. 28)
бар
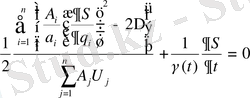 . (1. 29)
. (1. 29)
S функциясын
 , (1. 30)
, (1. 30)
түрінде ұсына отырып, (1. 29) -дан
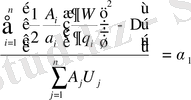 (1. 31)
(1. 31)
аламыз.
Енді
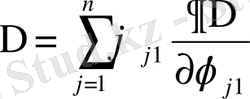 (1. 32)
(1. 32)
ұсына отырып, (1. 31) теңдеуінде (1. 25) формуласы
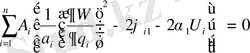 (1. 33)
(1. 33)
болады.
Егер
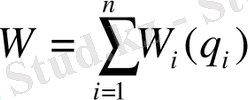 , (1. 34)
, (1. 34)
қойсақ, онда (1. 33) теңдеуі
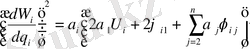 (1. 35)
(1. 35)
қанағаттандырылады.
Кейін, (1. 35) интегралдау арқылы (1. 26) формуласына келеміз. Теорема дәлелденді.
Егер гамильтонианда (1. 24)
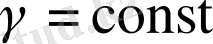 ,
,
 , онда В. Г. Деминнің теоремасына келеміз [16] .
, онда В. Г. Деминнің теоремасына келеміз [16] .
1. 5 Гравитацияланатын ортадағы тартылыстың бейстационарлық өрістегі материалдық нүктенің қозғалысы
Соңғы кездері аспан механикасының көптеген мәселелерінің ішіне квадратурадағы интегралдауға қызығушылық танылып жүр, оған екі қозғалмайтын центрдің есебі жатады. Жасанды жер серіктердің қозғалыс теориясын құруда гравитациялық өрісте, Жердің, Айдың және т. б. гравитациялық өрісіне жақындауы, сонымен қоса галактика тартылыс өрісінде жұлдыз-нүкте қозғалысын қарастыруда қозғалыстың дифференциалды теңдеуі квадратурада интегралданатын есепті құруға болады [13-16, 19-22, 27] .
Екі қозғалмайтын центрдің классикалық мәселесінен А. А. Кочиев консервативті күштің күш өрісінің бірінші класы үшін қозғалыс нүктесі есебін шешуді келтірді және аспан механикасы есебіне оның ұсынысын көрсетті [28] .
А. А. Беков және Т. Б. Омаровтың еңбектерінде үстемелі күш болған кездегі, сынақ дененің пропорционал жылдамдығымен және G жылдамдығының салыстырмалы өзгеруінде, G тұрақты тартылыс уақытпен айнымалы болғандағы екі қозғалмайтын центр есебін жалпылайтын бейстационарлы схемасын қарастырды. Жердің жасанды серіктерінің орбиталық қозғалысында айнымалы гравитация эффектіні талдауда аралық қозғалысты түсіндіру үшін есептердің мүмкін ұсыныстары көрсетілді [27] .
Т. Б. Омаров стациоанрлық есеп интегралды болса
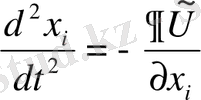 (1. 36)
(1. 36)
Мұндағы
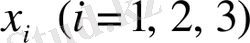 - тікбұрышты координаталар,
- тікбұрышты координаталар,
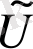 - жүйе потенциалы, онда бейстационарлы есеп те интегралды болатынын көрсетті.
- жүйе потенциалы, онда бейстационарлы есеп те интегралды болатынын көрсетті.
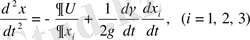 (1. 37)
(1. 37)
мұндағы
 - уақыттың үзіліссіз дифференциалды функциясы,
- уақыттың үзіліссіз дифференциалды функциясы,
 - бейстационарлы динамика жүйесінің потенциалы:
- бейстационарлы динамика жүйесінің потенциалы:
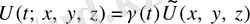 . (1. 38)
. (1. 38)
Гравитациялық өрістегі (1. 38) шаманың баяу өзгеруі кезінде жүйені шешуді (1. 37) сәйкес бейстационарлы есептегі аралық қозғалыс ретінде қарастыруға болады. Біз төменде осы идеяны жүзеге асырудың нақты мысалын келтіреміз. Сондай-ақ сәйкес теңдеу түрін (1. 37) интегралдауда Гамильтон-Якоби әдісі жүргізіледі.
Бейстационарлы гравитациялық өрістегі материалдық нүкте қозғалысы туралы есепті қарастырамыз
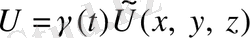 , (1. 39)
, (1. 39)
Мұндағы
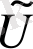 - көріністің күштік функциясы [6]
- көріністің күштік функциясы [6]
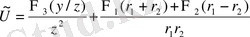 , (1. 40)
, (1. 40)
Мұндағы
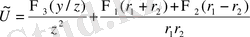 - өз аргументтерінің комплексті функциялары, мұндай
- өз аргументтерінің комплексті функциялары, мұндай
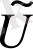 - шындық;
- шындық;
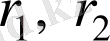 - екі қозғалмайтын центр нүктелерінің радиус-векторлары, яғни Ох остеріне симметриялы салыстырмалы координат басы орналасқан және тең
- екі қозғалмайтын центр нүктелерінің радиус-векторлары, яғни Ох остеріне симметриялы салыстырмалы координат басы орналасқан және тең
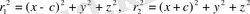 , (1. 41)
, (1. 41)
мұндағы c - ұзындық өлшемі бар параметр,
x, y, z - нүктенің тікбұрышты координаттары.
А. А. Кочиев [5] көрсеткендей, екі денелер есебінің потенциалы және қозғалмайтын центрлі екі денелер есебінің потенциалы (1. 40) потенциалдың жеке жағдайы ретінде алынуы мүмкін.
(1. 39) түрінің бейстационарлытігі тұрақты гравитациялық өзгеру мысалына негізделуі мүмкін.
Гамильтон формализмі көмегімен сәйкес дифференциалды теңдеуді интегралдау бұдан әрі ұйытқудың жақсы жасалған канондық теориясына көшуге мүмкіндік береді. Oxyz координаттары қозғалмайтын жүйеде бейстационарлы гравитациялық жүйеде болатын, нүкте қозғалысының диференциалды теңдеуі (1. 39) түрінде болады
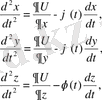 (1. 42)
(1. 42)
Мұндағы
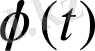 -уақыттың кейбір үзіліссіз функциясы.
-уақыттың кейбір үзіліссіз функциясы.
Енді формула бойынша
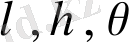 эллопсоидальды координаттарға көшеміз,
эллопсоидальды координаттарға көшеміз,
 (1. 43)
(1. 43)
мұндағы
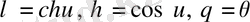 .
.
Енді жаңа айнымалы күш функциясын айтамыз (1. 39) .
Алдымен аңғаратынымыз, (1. 41) формуласы мына түрде болады
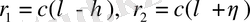 (1. 44)
(1. 44)
Енді, (1. 43) және (1. 44) формулаларын қолдана отырып,
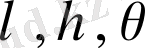 жаңа айнымалыда (1. 39) формуласын анықтайтын U күш функциясы үшін формула аламыз.
жаңа айнымалыда (1. 39) формуласын анықтайтын U күш функциясы үшін формула аламыз.
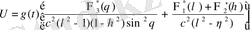 . (1. 45)
. (1. 45)
Кинетикалық энергия
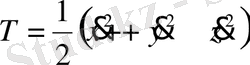 (1. 46)
(1. 46)
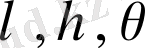 жаңа айнымалыда
жаңа айнымалыда
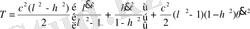 . (1. 47)
. (1. 47)
Әдеттегі түрдегі
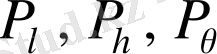 жалпылама импульсті жүргіземіз.
жалпылама импульсті жүргіземіз.
 (1. 48)
(1. 48)
Онда кинетикалық функция
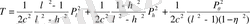 . (1. 49)
. (1. 49)
түрінде болады.
Гамильтон функциясы
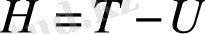 (1. 50)
(1. 50)
формуласымен анықталады. Және (1. 42) теңдеу жүйесі жартылай канондық түрді қабылдайды.
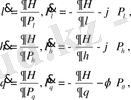 (1. 51)
(1. 51)
(1. 51) теңдеуін тікелей интегралдау мүмкін емес. Бірақ егер
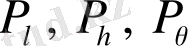 бірге
бірге
 жаңа айнымалыны келтірсе, онда теңдеу өрнігінің жалпы интегралы квадратура көмегімен табылады.
жаңа айнымалыны келтірсе, онда теңдеу өрнігінің жалпы интегралы квадратура көмегімен табылады.
Келесі айнымалыны ауыстыруды жасаймыз
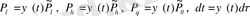 , (1. 52)
, (1. 52)
мұндағы
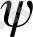 функциясы қатыспен қанағаттандырылады
функциясы қатыспен қанағаттандырылады
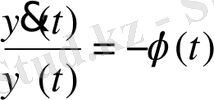 . (1. 53)
. (1. 53)
Онда (1. 51) теңдеуі жүйесін канондық формада жазуға болады
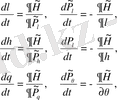 (1. 54)
(1. 54)
Яғни
 гамильтониан келесі түрде болады
гамильтониан келесі түрде болады
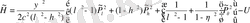 . (1. 55)
. (1. 55)
(1. 54) жүйесін интегралдауды Гамильтон-Якоби теңдеуінің толық интегралы арқылы жасаймыз.
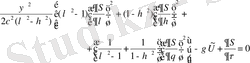 (1. 56)
(1. 56)
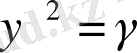 , (1. 57)
, (1. 57)
болсын делік, онда
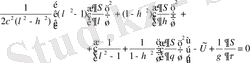 (1. 58)
(1. 58)
(1. 56) теңдеуінің толық инегралын мына түрде іздейміз
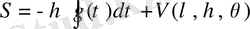 , (1. 59)
, (1. 59)
Мұндағы
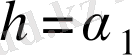 - еркін тұрақты,
- еркін тұрақты,
V - функция, мына түрге келтірілген
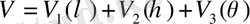 . (1. 60)
. (1. 60)
Шын мәнінде, (1. 56) теңдеуі (1. 60) формуласын қанағаттандыратын болады, егер
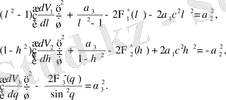 (1. 61)
(1. 61)
қойсақ.
Әрбір (1. 61) теңдеуінен бір ғана айнымалыны бөлуді интегралдау және тәуелсіз айнымалы болады. (1. 61) теңдеуін интегралдау арқылы келесі түрдегі (1. 60) теңдеуінің толық интегралын аламыз
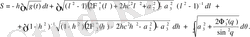 (1. 62)
(1. 62)
Енді Гамильтон-Якоби теоремасын қолдана отырып, формула бойынша
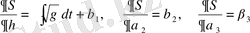 , (1. 63)
, (1. 63)
(1. 56) жүйесінің жалпы интегралын табамыз.
Мұндағы
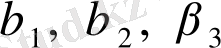 - жаңа еркін тұрақтылар.
- жаңа еркін тұрақтылар.
Жеке еркінді есептей отырып, есебіміздің жалпы интегралын келесі түрде жазамыз
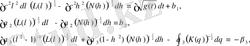 (1. 64)
(1. 64)
және
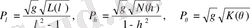 , (1. 65)
, (1. 65)
мұнда белгілер көрсетілген
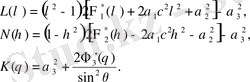 (1. 66)
(1. 66)
(1. 64) және (1. 65) теңдеулері (1. 57) және (1. 53) шарттарында қарастырып отырған бейстационарлы есептердің толық шешімін береді.
Уақыт функциясы ретінде эллопсоидалды координатты табу үшін (1. 51) жүйесінің (1. 65) және (1. 48) формуласынан алынатын бірінші интегралын пайдаланамыз.
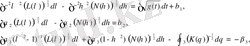 (1. 67)
(1. 67)
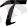 жаңа тәуелсіз айнымалыны
жаңа тәуелсіз айнымалыны
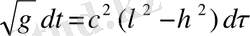 , (1. 68)
, (1. 68)
құрылғысы арқылы шығарамыз.
(1. 67) теңдеуін келесі түрде қайта жазамыз
 (1. 69)
(1. 69)
(1. 69) жүйенің бірінші екі теңдеуін интегралдау арқылы
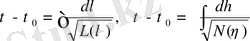 . (1. 70)
. (1. 70)
аламыз.
Эллиптикалық итегралмен айнымалыны табамыз
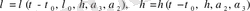 (1. 71)
(1. 71)
Содан кейін
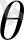 және t аралығындағы байланысты аламыз,
және t аралығындағы байланысты аламыз,
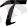 функциясы ретінде
функциясы ретінде
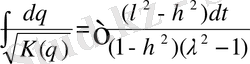 (1. 72)
(1. 72)
Онда,
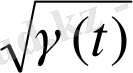 үшін өрнектеу ретінде
үшін өрнектеу ретінде
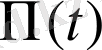 қолдана отырып,
қолдана отырып,
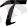 және t аралығындағы келесі түрдегі тәуелділікті аламыз.
және t аралығындағы келесі түрдегі тәуелділікті аламыз.
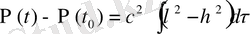 (1. 73)
(1. 73)
Енді классикалық мехканикадағы кейбір бейстационарлы есептер көрсетілген есептің жеке жағдайы ретінде алынуы мүмкін екенін көрсетеміз.
1. Мейлі функция
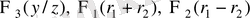 түрінде болсын
түрінде болсын
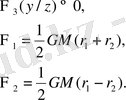
онда күш функциясы келесі түрде жазылады
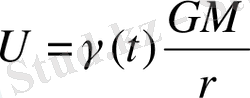 ,
,
Сонымен, біз қосымша күш (тартылыс күші) болған кездегі жалпы шешуі көрсетілген, екі денелердің бейстационарлы есебін алдық [27] .
2. Мына жағдайды қарастырайық, функция
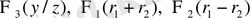 болғанда, мына түрде болады
болғанда, мына түрде болады
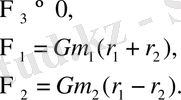
Онда, (1. 39) және (1. 40) формулаларына сәйкес
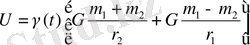
болады, және екі қозғалмайтын центр есебінің бейстационарлытігін аламыз.
Егер
 , а
, а
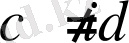 - нақты сан болса, онда жалпы шешімі алынған, екі қозғалмайтын центрлі жалпылама бейстационарлы есепті аламыз [8] .
- нақты сан болса, онда жалпы шешімі алынған, екі қозғалмайтын центрлі жалпылама бейстационарлы есепті аламыз [8] .
2 ЕКІ ҚОЗҒАЛМАЙТЫН НҮКТЕНІҢ МОДЕЛЬДІК ЕСЕБІ
2. 1 Гравитациялық өрістегі материалдық нүкте қозғалысының есептері
Гравитациялық өрістегі материалдық нүкте қозғалысының есептері қарастырылған, екі қозғалмайтын нүктенің модельдік есебі тақырыбына ұқсас жақын арада жарық көрген бірнеше жұмыстармен танысып шықтым [1, 2, 5, 29-33] . Жердің гравитациялық өрісіне жуық, мұндай қойылған есептер қозғалыстың дифференциялдық теңдеуінде квадраттық интегралдануы мүмкін.
Бұдан жаңа аспан механикасы есептерінің интегралдық жағдайларының табылғанын ойлауға болады. Бұрын белгісіздер жаңалық ашуға мүмкіндік беретіндей сенім туғызған және басқа жағдайларда аналитикалық қозғалыс есептері интегралданады (бұрыннан белгілі есептерден басқа, мұндағы күштің орталық өрісіндегі қозғалыс есептері және қозғалмайтын нүкте есептері) .
Бірақ ол үміт қазіргі кезде ақталмады. Себебі: Москвалық ғалымдар Е. А. Гребеников, В. Г. Демин және Е. П. Аксенов дәлелдеп көрсетті. Жоғарыда айтылған жағдайлардың интегралдануы тек материалдық нүкте қозғалысының жалпы әр түрлі дербес жағдайлардың жалпы есептерін ұсынады, екі қозғалмайтын центрлердің тартылуы яғни біз білетіндей эллипстік квадратта интегралданады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz