Техникалық жылудинамикасының әдістері

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 95 бет
Таңдаулыға:

Мазмұны

Әдебиеттер

1 Термодинамиканың бірінші заңы

1. 1 Жылу динамикасының негізгі заңдары

1. 1. 1 Техникалық жылудинамикасының әдістері

1. 1. 2 Жұмыстық дене күйінің көрсеткіші

1. 1. 3Біртекті идеалды газдарға арналған күй теңдеулер

1. 1. 4 Идеалды газдар қоспасы

1. 1. 5 Идеалды газдар және олардың қоспаларының жылусыйымдылығы

1. 2. 1 Жылулык пен жұмыстың эквивалентті принципі

1. 2. 2Қайтымды және қайтымсыз процесстер

1. 3Жылудинамикасыньщ бірінші заңын талдау формулалары

1. 4Жылу мөлшері

1. 5 Заңдар

1. 5. 1 Газ заңдары

1. 5. 2 Зат мөлшері және Авогадро тұрақтысы

1. 5. 3 Идеал газ күйінің теңдеуі

2 Термодинамиканың екінші заңы. Карно циклі

2. 1Айналмалы және циклдік процестер

2. 2Карно циклі

2. 3 Энтропия туралы ұғым

2. 4 Қайтымсыз процесс кезіндегі энтропияның өзгеруі

2. 5Тs - диаграмма

3 Сығымдағыш машинамен сығу процессі

3. 1Бірсатылы сығымдағыштар

3. 2Газдарды көпсатылы қондыргылармен сығу

3. 3Турбосығымдаушыдағы сығу процессі

4 Жылу маңыз алмасу

4. 1Конвективті жылуалмасу

4. 2Сәлелік жылу алмасу

5 Қазандық агрегаттар

5. 1Қазандық агрегаттардың топтасуы

5. 2 Қазандық қондырғы

5. 3 Іштен жанатын піспекті қозғалтқыштардың циклдары

5. 4 Газды турбина

5. 5 Регенеративті цикл

6 Ауыл шаруашылықта жылуды қолдану

6. 1 Отындар

6. 2 Жағушы құралдардың топтасуы

6. 3 Тоңазытқышты қолдану

6. 4 Пеш жағу

6. 5Кептіру технологиясы

6. 5. 1Кебудің мағынасы және кебу түрлері

6. 5. 2Материалдардың ылғалдылығы

Глоссарий

Жұмысшы дене . Механикалы және термиялық жұмысшы денесі ( газдың ) - негізгі параметрлер ( p, V, T) уақыттардың әрбір кезегіне көлемі барлық жерде бірдейді айтады.

Жылу техникасы - энергияны алу және қолдану ғылымын айтады.

Термодинамика - физиканың бір бөлімі, онда энергия механикалық жұмысқа немесе керісінше ауысуды айтады.

Температура (Т) - газдың орташа кинетикалық энергиясы.

Ішкі энергия - кез-келген денедегі барлық энергия.

Термодинамиканың бірінші заңы - энергияның сақталу немесе алмасу заңы.

Изохоралық процесс - көлем тұрақты жағдайдағы газдың өзгерісі.

Изобаралық процесс - қысым тұрақты жағдайдағы газдың өзгерісі.

Изотермиялық процесс - температура тұрақты жағдайдағы газдың өзгерісі.

Техникалық жылудинамикасының әдістері

«Жылудинамикасы» - грек сөзінен шыққан: «терме» - жылу, ыстьқ, от деген ceздepдi білдіреді, «динамикос» - күш, козғалыс, ал барлығы бipre - жылу (от) қозғалтушы күш. Сонымен, жылудинамикасы - жылу қозғалтқышының теориясы пайда болды. Техникалық жылудинамикасы - жылу мен өзара алмасуының заңдылығын зерттейді, ал, сонымен катар, осыған қатнасатын алмасуындағы дененің касиетінде зерттейді. Жылуалмасу теориясымен бipre, ол жылутехникасының теориялық негізі болады.

Денелердің жиынтығын, өзара әрекетте болуын, жүйелер деп атайды. Осы денелердің арасында, жұмыстық, дене, ерекше белгілерді, ол жылу мен жұмыстың өзара алмасу процессін жүргізеді. Қалғаны - коршаған орта кездері (немесе жылу сіңіргіштер) .

Жұмыстық, дене есебіне газдар мен булар жатады. Сұйыктармен салыстырғанда, газдар және булар, кыздыру және салкындату кезінде, кысымымен көлемі едәуір езгертіледі.

Техникалық жылудинамикасының әдістері үшін негізгі өзгешелігі жылудинамиканың процесстері мен жүйелерінің идеализацияда болуынан, процесстегі жұмыс жүйелерінің кебеюіне келтіреді. Мысалы, теңсалмақты жүйелер деп аталуын, оның уақыт аралығындағы өзгермеу касиетін немесе оның күйін зерттейді. Мұндай жүйелер, қоршаған ортадан бөлектендіріледі және сонымен катар, сыртқы күштің әсерінсіз, оның күйі сонша ұзақ, сакталуы мумкн. Мұндай жүйелерде, температураның барлықнүктелерінде бірдей, яғни жүйелердің жылу тепе-теңдігі орын алады. Егер жүйенің жеке бөлшектері бip - біріне қарағандағы алмасуы болмаса, онда, ол кезде кысымы мен тығыздығы жүйенің әр нүктелерінде бірдей болып механикалық тепе-теңдігі болады.

Сонымен қатар, тепе-теңдік жағдайының үздіксіз кезектілігінің түсініктілігі арқылы, оның күйінің өзгіруі кезіндігі, қаралып отырған жүйенің өтуінің тепе-теңдік процессі зерттеледі. Жеке жағдайда жорамалдау жолымен дәріптелінеді.

Процесстерді дәріптеу, жылудинамикасын зерттеуді оңайлатады. Сонымен бipгe, идеалды процесс -үлгі ретінде есептелінеді, оған практикалық, түрінде жетуге тырысу керек. Нақтылы процессте жүргізілетін жұмыстың істелуін, идеалды процесске сәйкес, жұмысты салыстырумен, сол процесстің мүлтіксіздігінше мүмкіндік береді. Техникалық, жылудинамикасына, нақтылы жағдайында, негізгі процесстерінің өтуінің каралуы eнгізіледі де, жылу техникасы курсының теориялық және практикалық бөлігі арасын байланыстырушы болып, шешуші рөл атқарады.

Жылудинамикасының негізін тәжірибемен анықталған екі заңы кұрайды - жылудинамикасының бірінші және екінші заңдары, олар техникалық жылудинамикасында жылу мен жұмыстың жеке күшінде колданылады.

Жұмыстық дене күйінің көрсеткіші

Біртекті жұмыстық дененің тепе-теңдікте тұрғандағы физикалық күйімен анықталатын, жиынтықты жылудинамикалың көрсеткіштерің негізіне - қысым Р, температура Т және меншікті көлемі V жатады. Олардың арасында байланыстары бар, оны аныктау үшін, әрбір жұмыстық денені тәжірибе жолымен немесе материяның кинетикальқ теориясы негізіндегі дененің салыстырмалы ішкі кұрылымын, кейбір жорамал түрінде анықтайды. Жалпы турінде көрсетілген керсеткіштердің аральқ қатынасы немесе теңдеу күйі мына түрінде болуы мумін:

f(P, V, T) = 0. (1. 1)

Тецдеу (1, 1) мына түрінде жазылады:

Р = f , ( V, T), V=f 2(P, T ), T= f 3(P, V ) . (1. 2)

Теңдеудің (1. 2) шығуы, бip мағыналы күйін анықтау үшін, барлық көрсеткіштері кажет емес. Оның үш шамасының Р, V, Т берілген екеуімен аныктауға болады. Осыған қарағанда, жұмыстық дене екі өстікординат жүйесімен бейнеленуі мүмкін, жиі Р ордината өсі бойынша және V өсі бойынша салынады; диаграммадағы әрбір нүктеге, оның бір белгілі күйіне сәйкес келеді. Қысым Р Паскалмен (Па) белгіленеді. Паскаль - қысым, 1м2 аудан бетіне нормаланған, бір қалыпты бөлінген 1 Н (Ньютон) күштің түсуін айтады немесе Па = Н/м2, мұндағы Н = 1 кг-м/с2. Қысым бірлігіне паскалдың еселі және бөлшекті сандарының жазылуы:

1 кПа (килопаскаль) = 103 Па;

1 МПа (мегапаскаль) = 106 Па;

1 мПа (миллипаскаль) = ІСГ3 Па және басқалар.

Бұрын қолданылған кейбір теңдіктерді, ал қазіргі кездегі қолданылатын қысымдардың және СИ бірліктері:

1 кгс/м2 = 1мм су бағанасы = 9, 8066 Па ~ 10 Па;

1 кгс/м2 = 98, 0665 кПа ~ 100 кПа = 0, 1 МПа;

1 атм = 101, 325 кПа = 760 мм сынап бағанасы (сын. бағ) ;

1 мм сын. бағ = 133, 322 Па ~ 133 Па;

1 бар. = 0, 1 МПа; ІМбар = 100 Па.

Қазіргі кездегі өлшеу техникаларындағы, сұйық қысымы мен газдар саласында қолданылатын өлшеу диапазоны өте кең - 1 пПа (пикопаскаль = 10~12 Па) дан 1ГПа (гигапаскаль = 109 Па) дейін.

Абсолютты қысым саласы - нөлден (абсалютты вакуум) және артық қысымға бөлінеді, яғни сұйық қысымы немесе газдардың қоршаған орта қысымының Ратм аралық айырмасы.

Практикалық жағдай нәтижелері бойынша, манометрдің көмегімен қысымды өлшеу мына формуламен анықталады;

р = р + р

мұндағы Рарт - атмосфера қысымынан артығы, манометрмен өлшенеді; Ратм - қоршаған орта қысымы (атмосфералық) Егер қысым Р атмосфералық қысымнан төмен болса:

р = р + р

мүлдағы Рвак - ауаның сиретілуі, вакуумметрмен өлшенеді.

Есте сақтау керек, атмосфералық қысым - ауыспалы шама, сондықтан техника саласында нормалы қысымды қолданады:

Р0=0, 101325 МПа.

Егер заттың көлемі V (м3), ал массасы m (кг), онда теңдеу:

V/m= (1. 3)

оны, заттардың меншікті көлемі деп атайды, (дене), оны м3/кг белгілейді. Дене (заттың) тығыздығы р деп, оның массасының m, көлеміне V қатынасы арқылы анықталу шамасын:

р=m/V. (1. 4)

Формуладағы т, кг; V - м3, р - кг/ м3. Формулалардағы (1. 3) және (1. 4) меншікті көлем мен тығыздығы арасында кері байланыс бар, яғни:

=1/р, немесе р=1. (1. 5)

Бұл шамалардың мәндері жылудинамикасының жағдайына байланысты. Жылудинамикалық температура Т, негізгі температуралық шама Кельвин (К) бойынша өлшенеді.

Сонымен қатар, жылудинамикалық температураны 1968 ж. Халықаралық практикалық температуралық шкала бойынша өлшейді де және оны Цельси (°С) градусы t белгілейді.

Жылудинамикасындағы жылудинамикасының көрсеткіштерінің күйін Т, жылудинамикасының температурасымен қабыл-дайды, және де әртүрлі нүктедегі есептеліну байланыстығын мына теңдеумен шешеді:

T=t + 273, 16. Практикалық есептеулер үшін T=t + 273 қабылдайды.

Біртекті идеалды газдарға арналған күй теңдеулер

Газдарды қолдану практикасын шартына қарай, техникалық жылудинамикасында нақтылы идеалды газдар үшін, тәжірибелік заңдылықты кеңінен қолданады. Сонымен, идеалды газ-шартты түрде газ болып есептелінеді де, олардың молекулаларының арасында, әрекеттестік күштер болмайды, ал молекулаларды көлемсіз ретінде қарастырады, дегенмен олар материалды бөлшектер. «Идеалды газ» ұғымы, жылудинамикалық зерттеулерді оңайлатады және төменгі қысымда (алмағайып қысыммен салыстырғанда) және жоғарғы температурада (алмағайып температурамен салыстырғанда), практикалық нәтижелердің тиімді дәлелдігін қамтамасыздандырады.

Одан кейінгі қарастырылатын, газдардың жылудинамикасы заңдылығына негізделгенде, нақтылы идеалды газдарға арналған.

Біртекті идеалды газдарға арналған теңдеулер, мына түрінде:

P /Т =Р2 /Т2 = Р /Т= const = R, (1. 6)

мұндағы R - меншікті газ түрақтылығы. Мұндағы шамалар мына бірлікте: Р - Н/м2, - м3/кг; Г-К, R- Дж/(кг-К) .

Теңдеу (1. 6) біртекті газдардың қалай болса солай алынған санына m арналғанын, басқа түріндегі (1. 3) теңдеуін пайдалана отырып жазуға бодады:

PV=mRT. (1. 7)

Бүл теңдеу, идеалды газдарға арналған Клайперон-Менделеев теңдеуі деп аталады. Мейлі, М газдың молярлы массасы, кг/моль, өлшенеді.

Авогадро заңы бойынша, идеалды газдың 10 3 көлемі - қандай да химиялық қүрамындағы р және tбірдей кезінде, дәл өзі болады. Белгілі, қысым кезінде = 101, 33 Па (760 мм. сын. бағ. ) және темпе-ратурадаT0=273, 16К (нормалы физикалық куйде), газ көлемі 10" моль кезінде, Vm = 22. 4116 м3. р^ Vm, Т0 жәнеМ=т мәндерін (1. 7) теңдеуіне ауыстырып қойып табамыз:

R* = MR =101, 33-22, 41 16/273, 16 = 8, 825- 103Дж/(моль-К) . (1. 8)

Мұндағы R барлық газдар үшін бірдей және оны, әмбебапты газ тұрақтылығы деп атайды. Сонымен:

R =R*/m. (1. 9)

Идеалды газдар қоспасы.

Жылулықты қолданатын машиналардьң жүмыстық денесі ретінде, әртүрлі газдардың қоспасын қолданады. Олар үшін, Rқос болуы қажет. Әрбір құрамды бөлікке кіретін қоспалар, қоспаның толық көлемімен толады, бірақ, онда олар өзінің парциалды қысымында болады:

Далътон заңы бойынша

P= P

Газды қоспаның т массасы үшін, дұрысында дәл осындай түріндегі теңдеу түрі (1. 7) :

PV = mRT.

Бірақта, меншікті газ түрақтылығы R, мұндағы қоспалар құрамына байланысты және бір және сол газдар қоспалары, олардың құрамдары өзгерген кезде, әртүрлі мәндерінде болады.

Қоспалардың, меншікті газ тұрақтыларын былай анықтайды. Қоспалар п, әртүрлі қүрамды бөлікті газдардан түрғандағы, әрқай-сысыньщ т\, т2, тз, . . . , тп массасында болғанда, қоспа массасын, мына түрінде шешеді:

т = т + т2 + m + . . . + тп = m (1-10)

Жеке құрамды (газдар) парциалды қысымдарды Р , Р2, Р , -•, Р деп белгілейді. Есте болу керек, газды қоспалардың, жеке газдардағы парциалды қысымы ұғымындағы қысым Рі; сол санында, сол көлемде және сондай температура кезінде, қоспа жағдайымен бірдей болуы тиіс. Сондықтан, біртекті газдар үшін мына теңдікте жүреді

Р V=т R Т. (1. 11)

Мұндағы Р , т , R - қаралып отырған газды қоспалардың парциалды қысымы, массасы, меншікті газ тұрақтылығы; V, Т-қоспаның көлемі мен температурасы.

Газды қоспаның әрбір құрамды бөлігіне жағдай теңдеулерін жазамыз:

P1V=m1R1T;

P2V=m2R2T;

PnV=mnRnT.

Осы теңдіктердің оң және сол бөліктерін мүшелеп қосып, табамыз:

(Р + Р2 + Р3+ . . . + Рп) V = (m R + m2R2 + m3R3 + . . . + тnR ) T.

Дальтон заңы негізіндегі, барлық құрамды бөліктегі парциалды қысымы газды қоспа қысымына тең:

Р = Р1 + Р2 + Р3+ . . . + Рn. (1. 12)

Солай болғандықтан, табамыз:

FV = (m R + m2R2 + m3R3 + . . . + mnRn) T,

m R + m2R2 + m3R3 + . . . + mnRn = mR деп белгілеп табамыз:

PV=mRT, (1. 13)

мүндағі

R = m R / m + m2R2/m + . . . + m R /m. (1. 14)

Қатынастар т\т = g , nii/m = g2, . . . т„/т = gn - газды

қоспалардың жеке кұрамды бөлшектерінің үлесі, сондықтан олардың жиынтығы:

g +g +……. +g =1

Бұдан, қоспаның меншікті газ тұрақтылығын, мына формуламен жазады:

R = g1R1+g2R2 + . . . +g R (1. 16)

Газды қоспаларды құрамды бөлшектерін молярлы үлеспен де жазады:

Nl + N2 + N3+ . . . + Na = N= mi/M = mM. (1. 16а)

Бұдан қоспаның орташа молярлы массасын М= 1/ g \M . Газ қоспаларының техникалық көрсеткіштерін, сонымен қатар, оның көлемдік құрамның көмегімен жиі анықтайды, оны анықтау былай қабылданған. Қоспа қысымы Р мен Т температурасы кезіндегі, әрбір қоспаның құрамды бөлшектерін жеке түрінде қарастырамыз. Сонымен, құрамды бөлшектердің парциалды көлемдері V V V , . . . Vn жағдай теңдеуіне сәйкес, қатаң түрде белгілі мәндерде болуы тиіс:

PV = m R T;

PV =m R T;

PVn = maRnT.

Осы теңдеулерді қосып, мүшелеп табамыз:

P(Vl+V2+V3+ . . . +V ) =

= (mlR1+m2R2 +m3R3 + . . . + mnRn) T=mRT. (1. 17)

Сонымен газды қоспа үшін PV=mRT, онда:

PV=P(Vl+V2+V3+ . . . +Vn) (1. 18)

немесе

V=V1+V2+V3+. :. . +Vn = Vi. (1. 19)

Формула (1. 19), газ қоспасының көлемдік құрамын анықтау негізіне жатады. Одан

V /V+ V2/V+ . . . +V V= r1+r2 +r3 + . . . +r = r = 1,

мұндағы V /V = r , V2/V = r . . . , V /V=r - газды қоспалардың жеке құрамды бөлшектерінің көлемдік үлесі.

Сонымен r = N /N (Vm = idem кезінде), M= r M және g = r М /М.

Газдың көлемдік құрамы, оның парциалдық қысымын тез анықтауға мүмкіндік береді. Қоспаның температурасы мен қысы-мын сақтағанда:

PV = m RT, .

ал қоспаның температурасы мен көлемін сақтаған кезде

PiV=miR T. Сондықтан P =V /(Vp) = r p. (1. 20)

Идеалды газдар және олардың қоспаларының жылусыйымдылығы

Денелердің жылу сыйымдылығы дегеніміз, оның температурасын 1°К өзгертуге арналған, қажетті жылу санын айтады. Заттардың санына байланысты, мына меншікті жылу сыйымдылығын пайдаланады: С -массалы жылу сыйымдылығы, бір килограмм массаның Дж/(кгК) жатуы; МС - молярлы жылу сыйымдылығы, I мольдың Дж/(к мольК) жатуы;

С - көлемдік жылу сыйымдылығы, 1 м3 Дж/(м3К) нормалы жағдайда жатуы:

С = С/ = С'/

P=const кезіндегі, массалы жылу сыйымдылығы, Ср - белгілейді жэне оны изобарлы деп атайды, ал V=constкезіндегісіи Cv -белгілеп және оны изохорлы деп атайды. Ср және Cv аралық байланысын Майер теңдеуі арқылы беріледі:

Ср-Су = R (1. 21)

Молярлы жылу сыйымдылығы үшін Майер теңдеуі, мына түрде болады:

Ср - Су=8, 314. (1. 22)

8, 314 - әмбебапты газ тұрақтылығы, кДж/(к мольК)

C /C =K

К- адиабаттар көрсеткіші.

Cv = R/K-1; Ср=K/-1. R. (1. 23)

Жылулык пен жұмыстың эквивалентті принципі

Жылудинамикасының бірінші заңы - энергияньң айналу және сақталуының жалпы заңдылығының жеке бір күйі, ол жылу мен механикалық жүмыстың, өзара өзгеріп айналу құбылысы кезіндегі, түрақты санды байланыстылығын анықтайды. Бүл формула жылу мен жұмыстың эквиваленттік принципі. Бірінші рет, энергияның сақталу заңы мен энергияның, айналу құбылысын 1748 жылы орыс ғалымы М. В. Ломоносов тұжырымдаған. Жүмыс пен жылулық арасындағы қатынастың бар екендігін, мына теңдеу көрсетеді.

0, 427 кгс. м = 4, 1868 Дж 4, 19 Дж. (2. 1)

Жұмыс және жылулық сандары Дж белгіленеді және оның

еселі және үлесті шамаларын - кДж (103Вт), МДж (106Дж) ; МДж

(10-3) және т. б; қуатты ватпен (Вт), кВт (1(Г3Вт), МВт (106Вт)

белгілейді.

қарастыралық. Жылулық эквиваленттің 1 кВт-сағ. 1ккал. санды мәндерін анықтау керек:

1. 1 кВт-сағ. =3600 қДж /4, 1868 = 860 ккал.

2. 340 г. /(кВт-сағ) тең меншікті отын шығынын бірлік СИ арқылы білдіру: 340/3600 = 0, 94 г/кДж.

3. Жылулық шығын 1 кВт-сағ. немесе меншікті жылулық шығыны 2500 ккал. /(кВт-сағ. ) тең. 1кВт-сағ. Жатқызылған СИ бірлігіне сәйкес шығынын анықтау керек: 2500-4, 1868 = 10475 кДж/(кВт-сағ. ) .

Меншікті жылулық шығынды қатынас түрінде шығарады: ; 2500-4, 1868/3600 = 2, 91 (кДж жылулық) /( кДж жүмыс) .

4. Қозғалтқыштан шыққан жұмыстық будың жылуын пайдалану кезінде, алынған электр энергияеының өндірілуі, әрбір мегакалория жылулығы е=0, 6кВт-сағ. /Мккал. -ға тең, кВТ-сағ/МДж ауыстыру керек:

е = 0, 6/4, 1868 [кВт-сағ/Мкал-Мкал/мДж] = 0, 143 кВт-сағ/МДж. 1 Дж жылулықтың электр энергиясын өндіру мына түрінде жазылуы мүмкін:

= 0, 6/4, 1868-3600/103 [кВт-сағ/Мкал-Мкал/мДж-МДж/ кВт-сағ] = = 0, 372 МДж жұмыс/МДж жылулық.

Қайтымды және қайтымсыз процесстер.

Механикалық энергияны жылуға (үйкеліс жолымен, соғу және басқа) тез айналдыру белгілі, бірақ жылулықты механикалық энер-гияға айналдыру оңай емес. Ол үшін күрделі қүрылғымен, инженерлік қондырғы қажет. Одан, жүйеден жылу бөлігін алып кетіп, оны түрлендірусіз жүмысқа айналдыру. Бұл жердегі, теңсіз бағалы жылулық, кері бағытпен ағуы - сыртқы күйіне байланыстылығы, сипатталады.

Мұндай түрдегі қайтымсыздық, дәл осындай болуы, соңғы температуралары кезіндегі, дене аралық жылу алмасу процессінде өтеді. Жылу өтуі, әр уақытта ыстық денеден аз қызған денеге, өзінен өзі тез өтеді, бірақ, кері процесс үшін қосымша жұмыс шығынын қажет ететін, салқынатқыш қондырғы керек.

Жұмыстық дененің тепе-теңдік күйін өзгерту үшін, жылулық теңдігін (газдың барлық массаларындағы температураларының, әрбір нүктелерінің процессінде бірдей болуы) және механикалық (әрбір нүктедегі процесстері газдың барлық массаларындағы қысым, бірдей болуы шарт) жағдайын сақтау керек.

Бүл, идеалды жағдайға жетуі мүмкін, мысалы, цилиндрдегі піспектің шексіз баяу қозғалыс кезінде, олардың қысымы барлық газдар көлемінде түрақталып үлгеруі тиіс. Піспекке тез немесе секірмелі түрде түсуінен, қысымның өзеруі, піспек жанындағы газ қысымы көп болғанмен, одан қашықтаған сайын азаяды.

Жылулықтың тепе-теңдікке жетуі үшін, болжау қажет, жылу көзімен, газдың аралығындағы температураның, шексіз аз айырмашылығы кезіндегі, процесстің әр нүктесіне жылу берілуі жүргізіледі. Сонымен, сірә, әртүрлі температураға өтуін қайтарымды процесстерді жүргізу үшін, кезінде, әртүрлі температуралардағы шексіз өте көп, санды жылу көзінің шегін - қажет етеді.

Механикалық және жылулықтағы Р, V, Т - негізгі көрсеткіш-терінің тепе-теңдігі жағдайының өзгеруіне қарай, олар уақыт аралығында ауыспалы, бірақ газдардың орналасуындағы әрбір, моменттегі барлық көлемі бойынша бірдей болады. Егер, тепе-теңдік процессінің не мына, не басқа багытта пайда болмауы, сол жумыстық денеде қалған соңғы өзгеруін қошаган ортадагы қайтымдылыгы деп аталады. Осы жагдайларды қанагаттандырмаса, онда қайтымсыз деп аталады. Тепе-теңдік процесс, қайтымсыз болуы мүмкін, мысалы үйкеліс бар болғанда, қоршаған ортадағы жылудың жоғалуы кезінде өтеді.

dL=pdh=pFdh. (2. 2)

Тепе-теңдік жағдайындағы жүйелер көрсеткіштерін бір мағыналы сыртқы жағдайымен анықтайды. Егер, жүйе өзінің жағдайын өзгерткен кезде, сыртқы жұмысты атқарады. Олай болса, тепе-теңдік жағдайындағы ол, жүмысты сол жүйенің көрсеткіштері арқылы білдіріледі. Целиндрдің ауданы F болғандағы газдың піспекке, Р қысымымен қамтамасыз етілуіндегі Р = р. F тең болады (2. 1 сурет), онда, піспектің dh аздап жылжуы кезіндегі, газдың жасаған жү-мысын, мына теңдеумен анықтайды.

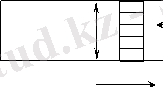
2. 1-сурет. Піспектің эрекетімен жасалынатын сыртқы жүмыс.

Бірақ, Fdh=dV көлемнің ұлғайуы болады. Сонымен жасалынған жұмыс:

dL = pdV. (2. 3)

Егер, тепе-теңдік жағдайы өзгеретін болса, онда dL жүйенің, көрсеткіштері арқылы жазуға болмайды. Р= pF сендіруге негіз жоқ, себебі, әрбір бөлігіндегі газ көрсеткіштері, әртүрлі және жүйенің тепе-теңдік жағдайындағы, оның мәндері тең емес. Бүл жерде сыртқы жағдайда, басқа тағы да бір немесе бірнеше қосымша көрсеткіштердің пайда болуы қажет (мысалы, тығыздықтың бөлінуі) . Тепе-теңдік процессті графикалық түрде түсіндірсек, себебі сызықты процесстердің Р, V, Т нүкте координаталары, әрбір уақыт моментінде дененің жылу динамикалық көрсеткіштерінің белгілі толық мәндеріне тең болады.

Жылудинамикасыньщ бірінші заңын талдау формулалары

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.