Санды теңсіздіктер: анықтамасы, қасиеттері және қосу мен азайту амалдары


Жоспар
1. Санды теңсіздіктер
2. Санды теңсіздіктердің қасиеттері
3. Санды теңсіздіктерді қосу және азайту
1. Санды теңсіздіктер
Сандарды салыстыру техникада, тұрмыста жиі қолданылады. Мысалы, машинаның бөлшегін жонып дайындаушы оның өлшемдерінің сан мәнін нақты (эталон) өлшемнің сан мәнімен салыстырады.
Салыстырылатын екі санның арасына > (үлкен) , < (кіші) немесе = (тең) белгілерінің біреуі қойылатынын білеміз.
Мысалы, 7>5; -7<7;
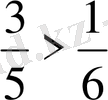 ; 46, 785>46, 783. 5
; 46, 785>46, 783. 5
> және < белгілері - қарама-қарсы теңсіздік белгілері. > мен > және < мен < белгілері - бірдей теңсіздік белгілері.
Мысалы, 6 > 0 және -1< 0 қарама-қарсы теңсіздік белгілері бар санды теңсіздіктер.
2 > 0 жөне 9 > 0 бірдей теңсіздік белгілері бар санды теңсіздіктер.
Теңсіздік белгісінің сол жағындағы өрнек теңсіздіктің сол жақ бөлігі деп аталса, оң жағындағы ернек теңсіздіктің оң жақ бөлігі деп аталады.
Теңсіздіктің сол жақ бөлігіндегі және оң жақ бөлігіндегі қосылғыштар оның мүшелері деп аталады.
Мысалы, 7, 5+3>5, 1+2 теңсіздігіндегі 7, 5+3 - теңсіздіктің сол жак белігі, ал 5, 1+2 - теңсіздіктің оң жак бөлігі; 7, 5; 3; 5, 1 және 2 - теңсіздіктің мүшелері.
Теңсіздік мағынасына қарай тура теңсіздік және тура емес теңсіздік болып бөлінеді.
Мысалы: 7, 5>7, 3 - тура теңсіздік; 6, 2<4 - тура емес теңсіздік.
Есептеулерде тура теңсіздіктер қолданылады, сондықтан «теңсіздік» сөзін ғана пайдаланамыз.
Санды теңсіздікте сандарды әріппен белгілесек, теңсіздік а> b; с<d түрінде жазылады. Мұндағы а, b, с және d - кез келген сандар (санды өрнектер) .
Есептеулерде қос теңсіздіктер де жиі кездеседі.
Мысалы, х>7 және х<10 теңсіздіктерін қос теңсіздікпен: 7<х<10 түрінде жазады. Жалпы түрде: а< b <с.
Бұл b саны а санынан үлкен, бірак с санынан кіші деген мағынаны білдіреді.
Сандарды салыстыруда үш түрлі жағдай кездеседі.
Олар: 1) а> b; 2) а< b; 3) а = b .
Берілген екі санды (санды өрнекті) салыстырғанда аталған үш жағдайдың біреуі ғана орын алады.
I. а саны b санынан үлкен, а> b.
Мысалы: а=0, 9 және £>=0, 4 сандарын салыстырайық.
Ол үшін а- b айырмасын табамыз:
а-b =0, 9-0, 4=0, 5; а-b =О, 5; 0, 5>0; а-b>0.
Берілген сандар үшін а- b айырмасы оң сан. Координаталық түзуде а санына сәйкес нүкте b санына сәйкес нүктенің оң жағында кескінделеді (1-сурет) .

1-сурет
Онда а> b екені белгілі.
а және b сандарын салыстырғанда а- b айырмасы оң сан болса, онда а> b .
ІІ. а саны b санынан кіші, а< b. Мысалы, а= 1, 3 және b =1, 5 сандарын салыстырайық. Ол үшін а- b айырмасын табамыз: а - b =1, 3-1, 5=-0, 2; -0, 2<0; а- b <0.
Берілген сандар үшін а- b айырмасы теріс сан.
Координаталық түзуде а санына сәйкес нүкте b санына сәйкес нүктенің сол жағында кескінделеді (2-сурет) .

2 -сурет
Онда а< b екені белгілі.
а және b сандарын салыстырғанда а- b айырмасы теріс сан болса, онда а< b;
III. а және b сандарының тең, яғни а= b болуы. Мысалы, 7=7; а=7, b =7, а- b =7-7=0.
Салыстырылатын екі санның айырмасы нөлге тең болса, онда ол сандар өзара тең.
Бұл жағдайда координаталық түзуде а саны мен b санына бір ғана нүкте сәйкес болатыны белгілі.
Егер теңсіздіктер > немесе < белгілерімен жазылса, онда теңсіздіктер қатаң теңсіздіктер деп аталады.
Мысалы: 9, 3<12; 8, 3>4 теңсіздіктері - қатаң теңсіздіктер.
Егер теңсіздіктер > немесе < белгілерімен жазылса, олар қатаң емес теңсіздіктер деп аталады.
Мысалдар: 1) Сыныпта бір күнде 6 немесе 6-дан аз сабақ болады. Сыныптағы бір күнгі сабак санын х -пен белгілесек, онда х =6 немесе х <6.
Мұндай жағдайда
х
 6 түрінде жазады. Яғни сыныптағы бір күнгі сабак саны 6-дан артық емес.
6 түрінде жазады. Яғни сыныптағы бір күнгі сабак саны 6-дан артық емес.
2) Жеңіл атлетика үйірмесінің бір тобындағы балалар саны 12-ден кем емес, бірақ 16-дан артық емес.
Жеңіл атлетика үйірмесінің бір тобындағы оқушылар санын
у
-пен белгілесек,
у
 12;
у
12;
у
 16. Онда 12
16. Онда 12
 у
у
 16. 12
16. 12
 у
у
 16 -
қатаң емес қос теңсіздік.
16 -
қатаң емес қос теңсіздік.
2. Санды теңсіздіктердің қасиеттері
Санды теңсіздіктерді теңбе-тең түрлендіруде санды теңсіздіктердің қасиеттері пайдаланылады. Сондықтан санды теңсіздіктердің қасиеттерімен танысып, оны есептеулерде пайдалануды қарастырайық.
1-қасиет.
Егер
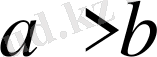 болса, онда
болса, онда
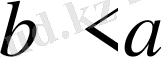 ; егер
; егер
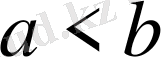 болса, онда
болса, онда
 .
.
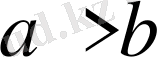 болғандықтан,
болғандықтан,
 , оң сан, онда
, оң сан, онда
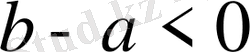 ; бұдан
; бұдан
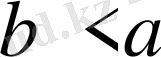 .
.
1-мысал. 5, 3>2, 7, онда 2, 7<5, 3.
Санды теңсіздіктердің 1-қасиеті бойынша, оның оң (сол) жақ бөлігі мен сол (оң) жақ бөлігін орындарын ауыстырғанда теңсіздіктің белгісі қарама-қарсы белгіге өзгереді.
2-қасиет.
Егер
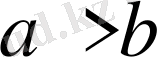 және
және
 болса, онда
болса, онда
 .
.
Салыстырылатын сандардың берілуі бойынша олардың айырмалары:
 ;
;
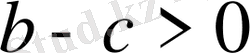 - оң сандар. Онда олардың қосындысы да оң сан.
- оң сандар. Онда олардың қосындысы да оң сан.
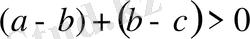 ;
;
 , бұдан
, бұдан
 , онда
, онда
 .
.
Координаталық түзуде, егер а санына сәйкес нүкте b санына сәйкес нүктенің оң жағында жатса, ал b санына сәйкес нүкте с санына сәйкес нүктенің оң жағында жатса, онда а санына сәйкес нүкте с санына сәйкес нүктенің оң жағында жатады (3-сурет) .
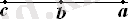
3-сурет
2-мысал. 9, 3<10; 10<21, 7; онда 9, 3<21, 7.
3-қасиет. Санда теңсіздіктің екі жақ бөлігіне де бірдей санды қосқаннан теңсіздік өзгермейді.
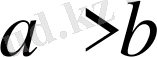 теңсіздігінің екі жақ бөлігіне де с санын қоссақ,
теңсіздігінің екі жақ бөлігіне де с санын қоссақ,
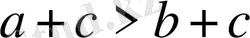 болады. (с - кез келген сан) .
болады. (с - кез келген сан) .
Бұл теңсіздіктің тура теңсіздік екенін тексерейік. Ол үшін:
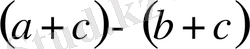 айырмасын қарастырайық.
айырмасын қарастырайық.
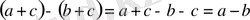 ;
;
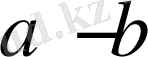 айырмасы - оң сан, себебі берілген теңсіздікте
айырмасы - оң сан, себебі берілген теңсіздікте
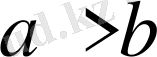 , онда
, онда
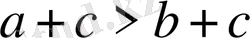 .
.
3-мысал. 1) 8, 9>5, 3 теңсіздігінің екі жақ бөлігіне де 1, 2 санын қоссақ, 8, 9+1, 2>5, 3+1, 2, 10, 1>6, 5.
2)
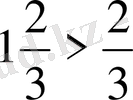 теңсіздігінің екі жақ бөлігіне де
теңсіздігінің екі жақ бөлігіне де
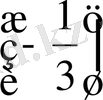 санын қоссақ,
санын қоссақ,
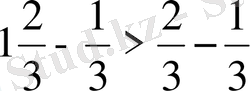 ;
;
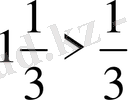 .
.
Санды теңсіздіктің бір жақ бөлігіндегі қосылғышты екінші жақ бөлігіне көшіргенде, оның таңбасын қарама-қарсы таңбаға өзгерту керек.
4-мысал. 7, 2+3>8, 1 теңсіздігін 7, 2+3-3>8, 1-3, яғни 7, 2>8, 1-3 түрінде жазуға болады.
4-қасиет. а) Санды теңсіздіктің екі жақ бөлігін де бірдей оң санға көбейтсек немесе бөлсек, теңсіздік өзгермейді.
І.
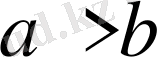 теңсіздігінің екі жақ бөлігін де
теңсіздігінің екі жақ бөлігін де
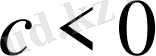 санына көбейтсек,
санына көбейтсек,
 теңсіздігі шығады. Бұл теңсіздіктіңтура теңсіздік екенін тексерейік:
теңсіздігі шығады. Бұл теңсіздіктіңтура теңсіздік екенін тексерейік:
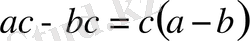 ,
,
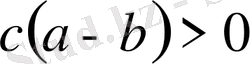 , себебі берілуі бойынша
, себебі берілуі бойынша
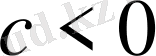 және
және
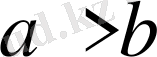 болғандықтан,
болғандықтан,
 , онда
, онда
 .
.
5-мысал. 1) 6, 2>9 теңсіздігінің екі жақ бөлігін де 2 санына көбейтсек,
6, 2 · 2 > 9 · 2,
12, 4<18.
ІІ.
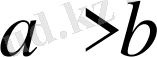 теңсіздігінің екі жақ бөлігін де
теңсіздігінің екі жақ бөлігін де
 санына бөлсек,
санына бөлсек,
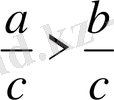 теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
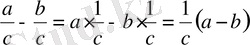 ;
;
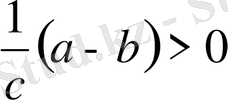 ; себебі берілуі бойынша
; себебі берілуі бойынша
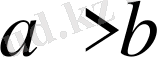 болғандықтан,
болғандықтан,
 және
және
 (екі оң санның көбейтіндісі де оң сан екенін еске түсірейік) . Онда:
(екі оң санның көбейтіндісі де оң сан екенін еске түсірейік) . Онда:
 .
.
2) 15, 5 : 5 > 10 : 5,
3, 1 > 2.
ә) Санды теңсіздіктің екі жақ бөлігін де бірдей теріс санға көбейтсек немес бөлсек, теңсіздік белгісін қарама - қарсы теңсіздік белгісіне өзгерту керек. Сол кезде ғана шыққан теңсіздік тура болады.
ІІІ.
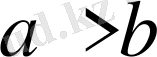 санды теңсіздігінің екі жақ бөлігін де
санды теңсіздігінің екі жақ бөлігін де
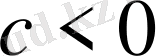 санына көбейтсек,
санына көбейтсек,
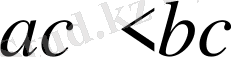 теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
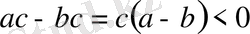 , себебі берілуі бойынша
, себебі берілуі бойынша
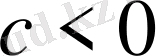 теріс сан,
теріс сан,
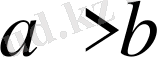 болғандықтан,
болғандықтан,
 оң сан. (Теріс санның оң санға көбейтіндісі теріс сан екенін еске түсірейік) . Онда
оң сан. (Теріс санның оң санға көбейтіндісі теріс сан екенін еске түсірейік) . Онда
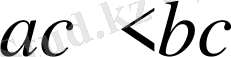 .
.
6-мысал. 1) 3, 1<2, 3 теңсіздігін (-2) -ге көбейтсек, 3, 1 · (-2) > 2, 3 · (-2) ; -6, 2 > -4, 6.
ІV.
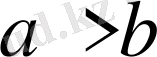 санды теңсіздігінің екі жақ бөлігін де
санды теңсіздігінің екі жақ бөлігін де
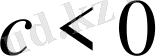 санына бөлсек,
санына бөлсек,
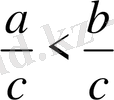 теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
теңсіздігі шығады. Бұл теңсіздіктің тура теңсіздік екенін тексерейік.
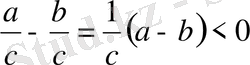 , себебі берілуі бойынша
, себебі берілуі бойынша
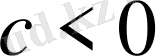 теріс сан болғандықтан,
теріс сан болғандықтан,
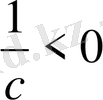 теріс сан,
теріс сан,
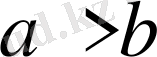 болғандықтан,
болғандықтан,
 оң сан. (Теріс санның оң санға көбейтіндісі теріс сан екенін еске түсірейік) . Онда
оң сан. (Теріс санның оң санға көбейтіндісі теріс сан екенін еске түсірейік) . Онда
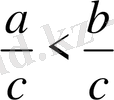 .
.
2) 12<7 санды теңсіздігінің екі жақ бөлігін де (-3) - ке бөлсек,
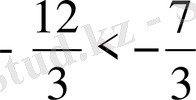 ;
;
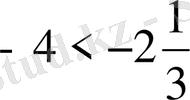 .
.
5-қасиет.
Егер
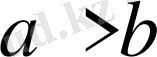
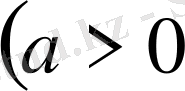 және
және
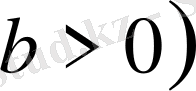 болса, онда
болса, онда
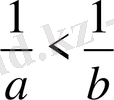 .
.
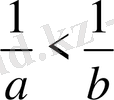 санды теңсіздігінің тура теңсіздік екенін тексерейік.
санды теңсіздігінің тура теңсіздік екенін тексерейік.
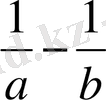 айырмасы - теріс сан.
айырмасы - теріс сан.
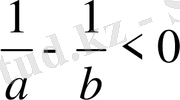 , себебі берілуі бойынша
, себебі берілуі бойынша
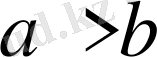
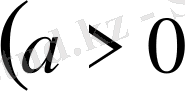 және
және
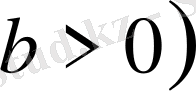 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz