ДИНАМИКА. МАТЕРИАЛДЫҚ НҮКТЕ ДИНАМИКАСЫНА КІРІСПЕ

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 81 бет
Таңдаулыға:

ДИНАМИКА.

МАТЕРИАЛДЫҚ НҮКТЕ ДИНАМИКАСЫНА КІРІСПЕ.

§1. Негізгі ұғымдар мен анықтамалар

Динамика деп күш әсерінен денелердің қозғалуын зерттейтін теориялық механиканың бөлімін атайды. Динамикада нүктенің, дененің қозғалысы күшке және нүктенің, дененің инерттігіне байланысты деп қарастырамыз.

Геометриялық тұрғыдан нүктенің, дененің қозғалысын кинематикада қарастырдық.

Динамикада да күш деп денелердің өзара механикалық әсерлесуінің өлшеуіші ретінде алынатын шаманы атаймыз.

Статикада тек тұрақты күштерді қарастырдық. Динамикада күштерді, сонымен қатар, уақытқа, жылдамдыққа, координаттарға тәуелді деп аламыз. Демек,

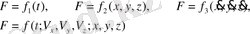
Мысалы, бір сәттен бастап, плотинаның суы көбейе бастасын. Судың плотинаға әсерін уақытқа тәуелді күш деп қараймыз. Демек

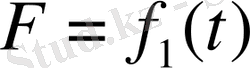
Екіншіден, мәшине айнымалы жылдамдықпен келе жатса, ауаның кедергісі мәшиненің жылдамдығына байланысты:

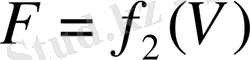
Гауһар тас жинаушыларға әсер ететін судың салмақ күші z тереңдік координатасына тәуелді.

Егер екі денеге бірдей күш әсер етсе, олар екі түрлі жылдамдық алып, екі түрлі орын алмастырады. Екі түрлі заңдылықпен қозғалады.

Күш әсерінен дененің жылдамдығы тезірек немесе бәсеңірек өзгеру қасиетін оның инерттігі деп атаймыз. Дененің өлшемі - масса.

Егер дененің кескіні (формасы) оның қозғалысына ешқандай әсер етпесе, оны нүкте деп қарап, материялық нүкте деп атаймыз.

Сонымен қатар, егер дененің өлшемдері оның орын алмастыру өлшемдерінен анағұрлым аз болса, онда денені материялық нүкте деп атаймыз.

Мысалы, зеңбіректің атылған оғын, Күнді айнала қозғалысында жерді материялық нүкте деп алуға болады.

§2. Динамиканың заңдары

Динамиканың заңдарын 1687 ж. өзінің “Табиғи философияның математикалық бастапқы негіздері” деген кітабында ағылшын оқымыстысы Исаак Ньютон бірінші рет жинақтап, келтіреді. Динамика заңдарының әділдігі адамзаттың тарихи тәжірибесімен дәлелденген.

Бірінші заң (инерция заңы) . Г. Галилей оны 1638 ж. ашқан. Егер материялық нүктеге ешбір күш әсер етпесе немесе әсер ететін күштер жүйесі нөлге парапар болса, онла нүкте тыныштық күйде немесе бір қалыпты тік сызықты қозғалыста болады.

Мұндай қозғалысты нүктенің инерциялық қозғалысы дейміз.

Инерциялық қозғалыс орындалатын санақ жүйесі инерциялық санақ жүйесіне жатады.

Көп жағдайда, бас нүктесі Күнде орналасқан, өстері қозғалмайтын жұлдыздарға бағытталған санақ жүйесі инерциялық санақ жүйесіне жатады.

Есеп шығарғанда, жермен байланысқан координаталар жүйесін инерциялық санақ жүйесі деп есептей беруге болады.

Ньютонның екінші заңы (динамиканың негізгі заңы) . Материялық нүктенің үдеуі әсер етуші күшпен бағыттас, модулі күштің модуліне пропорционал. Яғни

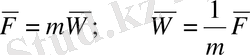
Егер денеге бірнеше күштер әсер етсе, олар бір тең әсерлі күшке парапар. Демек,

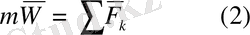
Үшінші заң. Екі нүкте бір-бірімен бір түзудің бойымен қарама-қарсы бағытталған, модульдері тең күштер арқылы әсерлеседі.

Төртінші заң (суперпозиция заңы) . Егер материялық нүктеге бірнеше күштер әсер етсе, онда олардың әрқайсысының нүктеге беретін үдеулері әр күштің өзіне ғана пропорционал, басқа күштерге тәуелсіз.

Демек, егер нүктеге күштер жүйесі әсер етсе, олар нүктеге

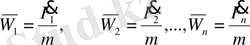
үдеулерін тудырады.

Теңдеулердің сол жағы мен оң жағын өзара қоссақ,

яғни немесе

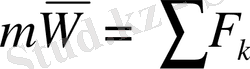
СИ халықаралық өлшем бірлігі бойынша, механиканың негізгі өлшем бірліктері былай аталады:

ұзындық өлшем бірлігі - 1м,

уақыт өлшем бірлігі - 1с,

масса өлшем бірлігі - 1 кг. Онда күш өлшем бірлігі

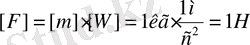
1 Ньютон күш - 1кг массаға 1 м/с2 үдеу беретін күш.

Егер өлшем бірліктері 1 гр, 1с, 1см болса, онда

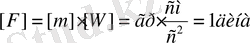
§3. Еркін және еркін емес нүкте динамикасының екі мәселесі

Динамикада екі мәселе қарастырамыз.

Бірінші мәселе. Егер еркін нүктенің

Қозғалыс заңы берілсе,

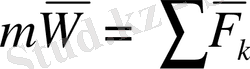
теңдеуі арқылы қозғалысты тудырған күшті табу.

Екінші мәселе. Егер әсер ететін күш белгілі болса, онда нүктенің (2) қозғалысын табу. Екінші мәселені, көп жағдайда, динамиканың негізгі мәселесі деп атаймыз.

Егер еріксіз нүктенің қозғалысын қарастырсақ, динамиканың негізгі заңы келесі түрде жазылады

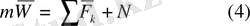
Бұл жағдайда мәселелер төмендегідей болады.

Бірінші мәселе. Нүктенің (2) қозғалыс заңымен қатар белсенді күштер берілсе, реакция күшін табу.

Екінші мәселе. Егер актив күштер белгілі болса, (2) қозғалыс заңын және реакция күшін табу.

Мысалы : Салмағы Р ауалық шар а үдеумен төмендесе, тура сондай үдеумен көтерілуі үшін шар салмағын қандай Q ауырлық күшке азайту қажет?

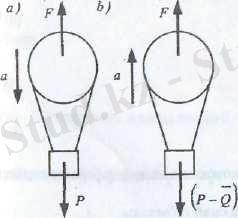
Шешімі: Түсіп келе жатқан шарға көтеру күші және ауырлық күші әсер етеді. Динамиканың екінші заңын тік түзуге проекцияласақ,

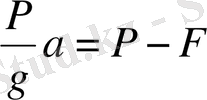
Ауырлығы балластысын түсіргеннен кейін, ауырлық күш болады. Шардың көтеру күші , демек

.

Бірінші теңдеудегі Ғ күшті екінші теңдеуге қойғаннан кейін

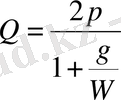
МАТЕРИЯЛЫҚ НҮКТЕ ДИНАМИКАСЫ

§1. Материалдық нүктенің дифференциалдық теңдеулері

Кез келген массасы m нүктенің тік бұрышты координаттар жүйесіндегі қозғалысын қарастырайық. Нүктеге

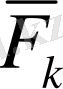
Күштер әсер етсе, оның қозғалысы динамиканың негізгі теңдеуімен

(1)

Беріледі.

Бұл теңдеудің x, y, z өстеріне проекциялары

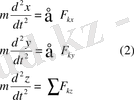
болады.

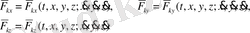
(2) -жай дифференциалдық теңдеулердің әр қайсысы екінші ретті болғандықтан, үш теңдеудің әр қайсысын интегралдағанда алты интегралдық тұрақтылар пайда болады. Демек, (1) теңдеулер шешімі осы алты тұрақты шамаларға тәуелді:

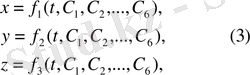
Интегралдық тұрақтылар бастапқы уақытқа байланысты шарттардан табылады. Мысалы, t=0 бастапқы уақыт болса, осы уақыттағы координаталар және жылдамдықтар

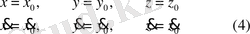
бастапқы шарттар деп аталады.

Сонымен қатар

бастапқы координаттар деп,

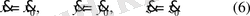
бастапқы жылдамдықтар деп аталады.

теңдеулер тік бұрышты координаталар жүйесіндегі нүкте қозғалысының дифференциалдық теңдеулері деп аталады. .

Ондай теңдеулер басқа да, мысалы, табиғи санақ жүйесінде де оңай табылады:

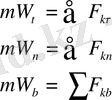
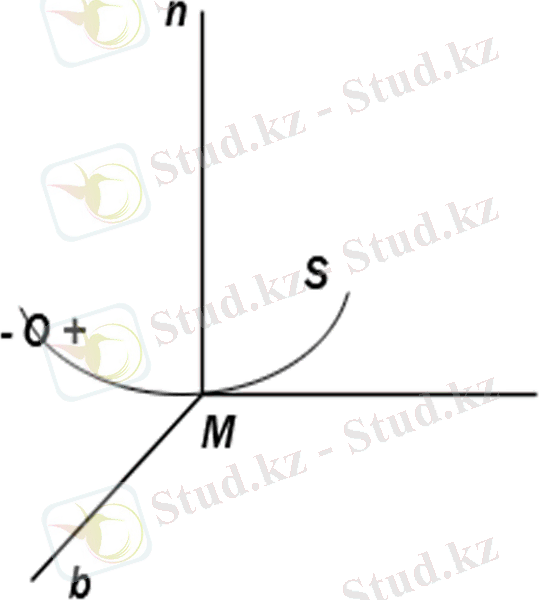
немесе

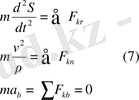
(7) - нүкте қозғалысының табиғи координаталар жүйесіндегі теңдеулірі деп аталады.

§2. Материялық нүктенің түзу сызықты қозғалысы

Нүкте түзу сызықты қозғалыста болса, әсер етуші күш пен үдеу сол сызықтың бойымен бағытталады және бастапқы жылдамдық та сол сызықпен бағытталуы қажет.

Мысалы, нүкте х координата бойымен күштер әсерінен қозғалсын. Динамиканың екінші немесе негізгі мәселесін шешу үшін нүктенің қозғалыс заңын табуымыз қажет.

1) . болсын.

Нүктенің дифференциалдық

теңдеуі белгілі

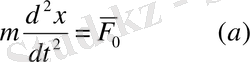
Яғни

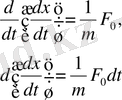
Екі жағынан интеграл алайық:

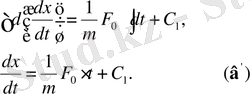
Тағы да екі жағын dt - ға көбейтіп, интеграл алайық

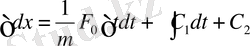
Онда

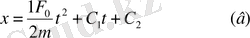
(в) - (а) теңдеуінің жылпы шешімі. С1, С2-интегралдық тұрақтылар бастапқы шарттардан

табылады. (в’) -тен: , (в) -дан . Онда

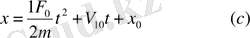
. Демек, нүкте тұрақты күш әсерінен тұрақты үдеумен қозғалады.

2) (a) делік, демек күш тек уақытқа ғана тәуелді . Онда

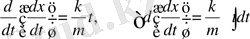
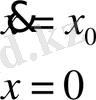
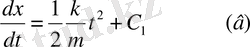
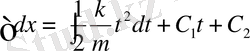
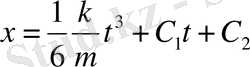
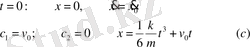
Күш тек қана жылдамдыққа тәуелді.

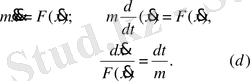
Теңдеудің екі жағынан да интеграл алсақ

, демек

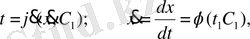
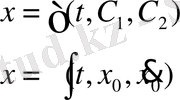
күш нүкте орнына (координатасына) тәуелді болсын:

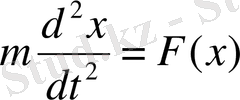
Теңдеудің сол жағын түрлендірейік

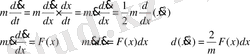
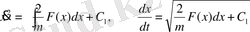
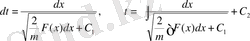
§3. Көлденеңге көлбеу тасталған нүктенің қозғалысы

Көлденеңге бұрышпен тасталған

бастапқы жылдамдығы , массасы m

денені нүкте деп қарастырып, оның

қозғалысын зерттейік. Бастапқы t=0

кезде М нүктені координаттар

жүйесінің О бастапқы нүктесінде деп

алайық:

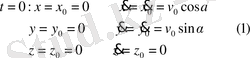
Нүктеге тек ауырлық күші әсер етеді дейік. Нүктенің қозғалысында ауаның кедергісі жоқ деп қарастырайық. Онда қозғалыстың дифференциалдық теңдеулері келесі түрде жазылады:

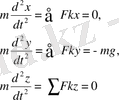
немесе

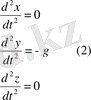
Алдымен бірінші теңдеуді интегралдайық:

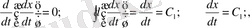
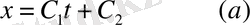
- белгісіз интегралдық тұрақтылар бастапқы (1) шарттардан табылады:

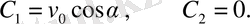
Онда

(3)

- жүйенің екінші теңдеуін интегралдасақ,

(в)

мұнда

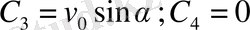
Яғни

(4)

(2) -жүйенің үшінші теңдеуінен

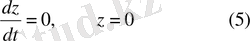
Егер қозғалыстың

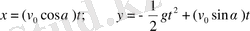
теңдеулерінен t шаманы жойсақ

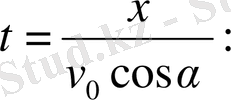
немесе (6)

болады.

Демек, нүктенің траекториясы-тік өсті парабола.

Кедергісіз кеңістікте көлденеңге бұрышымен көлбеу тасталынған материялық нүктесінің траекториясын кезінде Галилей тапқан.

Нүктенің көлденең ұшу Х қашықтығын табу үшін y=0 нүктелерді табу керек.

Демек, .

Онда

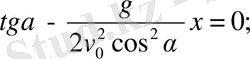
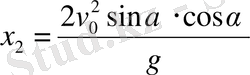
Яғни

(7)

Нүктенің ұшу Т уақыты теңдеуінен табылады. Шанында да

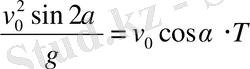
яғни

(8)

Нүктенің ұшу Н биіктігін

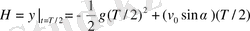
теңдеуден табамыз:

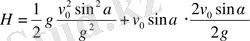
Демек,

Бұл алынған қорытындыларды ұщу қашықтығы 200-600 км снарядтардың, ракеталардың ұшу сипаттамаларын жуық есептеуге пайдалануға болады. Ал немістердің ФАУ-2 снарядын тік көтеріліп, 20 км биіктікте 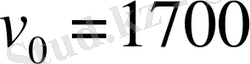м/с жылдамдықпен, 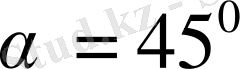бұрышпен ауасыз кеңістікте тасталған дене деп қарастырсақ, сипаттамалары келесідей болады.

Бұл шамалар ФАУ-2 снарядтың сипаттамаларына өте жақын.

МАТЕРИЯЛЫҚ НҮКТЕНІҢ ТҮЗУ СЫЗЫҚТЫ ТЕРБЕЛІСІ

§1. Нүктенің түзу сызықты еркін тербелісі

Уақытқа байланысты қайталанып отыратын қозғалысты “тербеліс” деп атаймыз. Мысалы алтыбақан қозғалысы, бесік қозғалысы тербеліске жатады.

Тербеліс қозғалыстары механикада, физикада, жалпы табиғатта кең таралған қозғалыстар. Мысалы, электронның тербелісі, серіппенің ұшына бекітілген жүк тербелісі, су-газ тербелісі, жүрек тербелісі.

Тербеліс қозғалыстары қайтарушы күштер әсерінен туады. Қайтарушы күшке серіппенің серпімділік күші,

тартылыс күштері, тағы да басқа күштер жатады.

Тепе-теңдіктегі орнынан ауытқыған материялық нүктені сол орнына қайтаруға әрекет ететін күшті қайтарушы күш деп атаймыз.

Қайтарушы 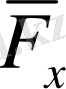күшінен туатын нүктенің түзу сызықты қозғалысын қарастырайық. Егер ауытқу аз шама болса, күштің х өсіне проекциясы

(1)

деп алынады. с - қатаңдық еселігі, серіппені бірлік ұзындыққа созатын күш. Ньютонның екінші заңына сәйкес нүктенің түзу сызықты қозғалысы

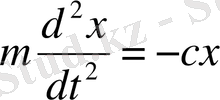
дифференциалдық теңдеуімен беріледі. Теңдеудің екі жағын m шамаға бөлсек, деп белгілесек,

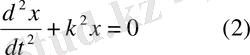болады.

Бұл теңдеуді нүктенің еркін тербелісінің дифференциалдық теңдеуі деп атаймыз.

Демек, егер нүктеге қайтарушы 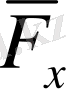күштен басқа күштер әсер етпесе, онда нүкте еркін тербелісте болады.

(2) дифференциалдық теңдеудің х шешімі

Мұнда 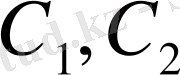-интегралды тұрақтылар. (3) -тің орнына

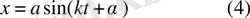
функциясын алуға болады.

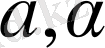-интегралды тұрақтылар. мен тұрақтылардың механикалық мағынасын түсіну үшін нүктенің шеңбермен қозғалысын қарастырайық.

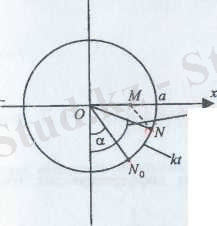Бастапқы t=0 уақытта N ₀ орында, ал кез келген t уақытта N орында болсын. Ол N ₀ , N нүктелер бұрышпен және k бұрыштық жылдамдықпен анықталады. N нүкте шеңбер бойымен қозғалғанда х осіне проекциясы М (а, -а) аралығында өзгереді. а-нүктенің х бойымен ең үлкен ауытқуы. Оны амплитуда деп атаймыз. 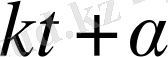- бұрыштық фаза деп аталынады; - бастапқы бұрыштық фаза. Олар нүктенің бастапқы және кез келген t уақыттағы х өсіндегі орындарын көрсетеді.

k еселікті дөңгелектік еселік деп атаймыз. Нүктенің k шеңберді k толық бір айналу t=T уақытын айналым дейміз. Демек,

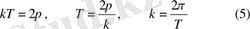
Нүктенің 1 секундтағы толық тербелісінің санын v деп белгілесек,

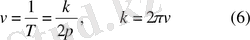
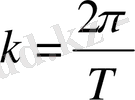-нүктенің секундтағы толық қозғалысының саны.

v-жиілік деп аталады.

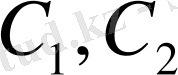немесе 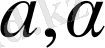есептің

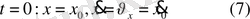
бастапқы шарттарынан табылады.

Мысалы, 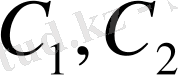-тұрақтыларды табу үшін

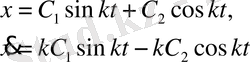(8)

-екі теңдеуді қарастыру керек. Онда

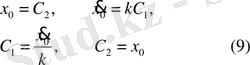
Демек

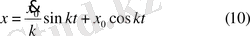
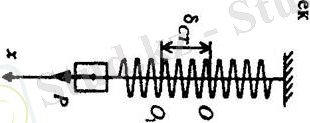Тұрақты күш әсерінен нүктенің еркін тербелісін қарастырайық. Нүктеге қайтарушы күшпен қатар сан мәні мен бағыты тұрақты Р күш түссін. Онда нүктенің тепе-теңдік орны О нүктеден О ₁ нүктеге көшеді. Сонымен қатар 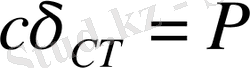деп алынады; -статикалық ауытқу. Қайтарушы күш 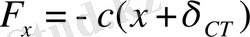. Нүкте тербелісінің дифференциалдық теңдеуі

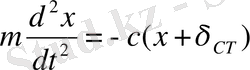
немесе

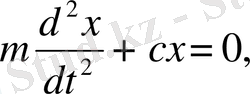
яғни

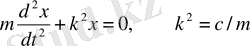Есептің бастапқы шарты келесі түрде жазылады

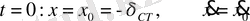Бұл жағдайда келесі теоремаға келеміз.

Теорема . Тұрақты күш әсерінен нүктенің еркін тербелісінің дифференциалдық теңдеуі өзгермейді. Одан нүктенің тек тепе-теңдік орны өзгереді.

§2. Материялық нүктенің кедергілі ортадағы өшпелі тербелісі

Нүктенің еркін қозғалысында 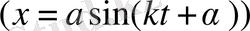бір басталған тербеліс тоқтаусыз орындала береді. Нүктенің қозғалыс ортасын кедергілі деп қарастырайық. Орта кедергісі 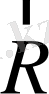жылдамдықтың бірінші дәрежесіне пропорционал болсын:

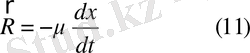
Мұнда 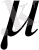- тұтқырлық еселігі орта кедергісін сипаттайды.

Онда динамиканың екінші заңы былай жазылады:

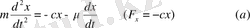
Егер 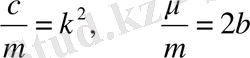белгілерін енгізсек, (a) теңдеуі былай жазылады:

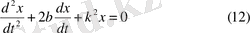
Бұл теңдеуді нүктенің өшпелі тербелісінің дифференциалдық теңдеуі дейміз (сызықты, екінші ретті жай дифференциалдық теңдеу)

(12) -нің сипаттамалық теңдеуі

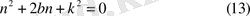
Теңдеудің түбірлері

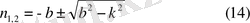
Бұл теңдеудің екі жағдайын қарастырамыз.

1-жағдай: (b-ортаның кедергісі, k-серіппенің серпімділігін сипаттайды) кедергі аз жағдай. Онда

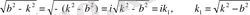
демек,

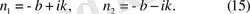
онда

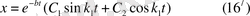
немесе

(16) -нүктенің өшпелі қозғалысының теңдеуі.

Өшпелі тербелістің айналымы

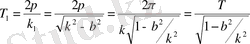
Яғни

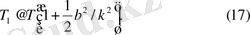
Демек, 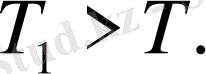Егер k>b болса

Демек, әр кедергі аз айналымға әсер етпейді.

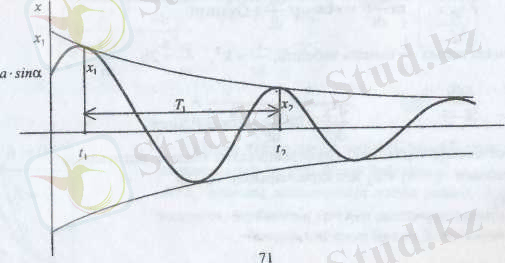
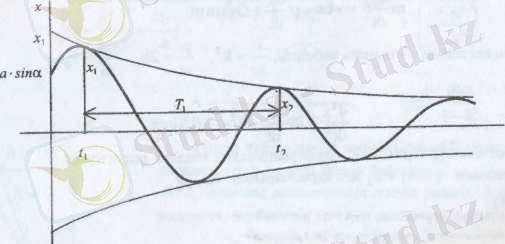
Егер 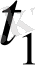уақытқа сәйкес бірінші ең үлкен ауытқу 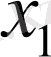болса,

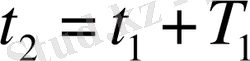уақытқа сәйкес ауытқу 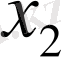болса, онда

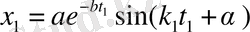
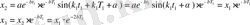
Демек,

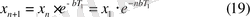
(19) - дан байқайтынымыз өшпелі тербелістің амплитудасы айырымы 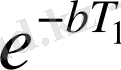геометриялық прогрессиямен кеміп отырады. 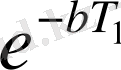- тербеліс декременті, 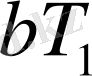- тербелістің логарифмдік декременті делінеді.

2-ші жағдай . Егер b>k, онда

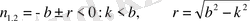
Онда тербелістің дифференциалдық теңдеуінің шешімі

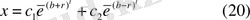
Яғни кедергі күші серпімділік күштен көп болса нүкте тербеліске шыға алмайды.

3-жағдай. Егер r=0, b=0 болса болады, - айналымсыз қозғалысқа келеміз.

Дәріс-19. МАТЕРИЯЛЫҚ НҮКТЕНІҢ ТҮЗУ СЫЗЫҚТЫ ТЕРБЕЛІСІ (ЖАЛҒАСЫ)

§3. Материялық нүктенің мәжбүр тербелісі

Нүктеге қайтарушы 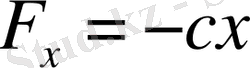, кедергі 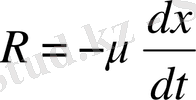күштермен қатар мәжбүрлеуші күш әсер етсін. Мәжбүрлеуші немесе ұйытқушы күшті гармониялық түрде алайық, мысалы

Онда

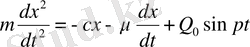
Теңдеудің екі жағын 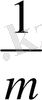шамаға көбейтіп, 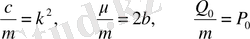деп білгілесек,

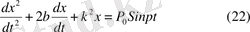
(12) еріксіз немесе мәжбүр тербелістің дифференциалдық теңдеуі деп аталады.

(12) теңдеудің шешімін 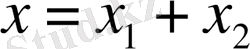деп қарастырамыз.

Мұнда

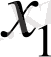
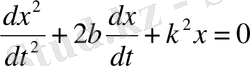
теңдеудің шешімі. Теңдеу біртекті дифференциалдық деп аталады. 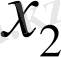- (22) -ның кез келген дербес шешімі:

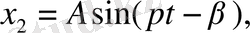
А, 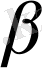-тұрақтылары (22) - теңдеуді қанағаттандыратын етіп іздеу керек. 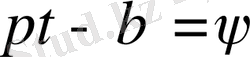десек,

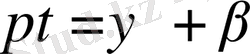
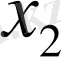-нің туындылары ;

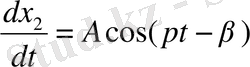Оларды (22) қойсақ,

Онда

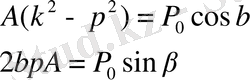
теңдеулердің екі жағын квадраттап, өз өсімен қоссақ,

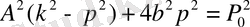болады.

Бұл теңдеуден А амплитудасы мен 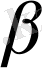фаза келесі түрде табылады

(22) мәжбүр тербеліс дифференциалдық теңдеуінің шешімі нәтижесінде

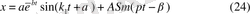
Мәжбүр тербеліс, сонымен, күрделі қозғалыс. Ол жүйенің 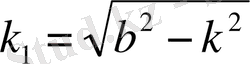жиілікпен меншікті өшпелі 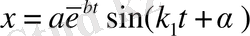тербелісімен р жиілікті

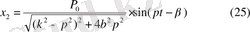
тербелісінен құралады.

Меншікті тербеліс уақыттың өсіне сәйкес азайып отырады да белгілі бір кезде толық өшеді-амплитудасы нөлге айналады. Ақырында (24) нүкте тербелісі (25) мәжбүр тербеліске шығады.

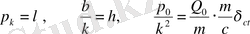
деп белгілейік. Онда

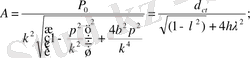
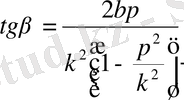
демек,

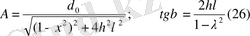
Соңғы теңдеуден А және 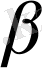шамалардың 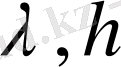өлшемсіз параметрлерге тәуелді екенін байқаймыз.

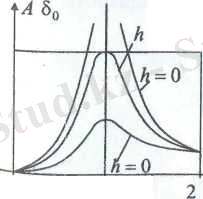
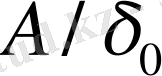шаманы динамикалық еселік дейміз, 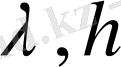шамаларды өзгертсек, тербелістің әр түрлі амплитудаларын аламыз.

h кедергі аз шама болып, 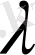бірліктен аз болса,

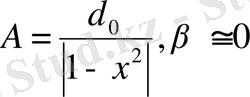
Тағы да басқа жағдайларды қарастырайық.

1) 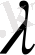- өте аз шама. 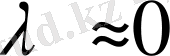. Онда

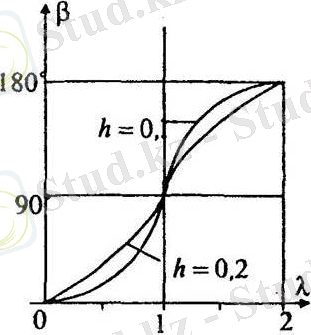
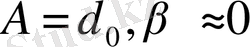
2) , h - аз шама делік. Онда

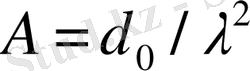
3) 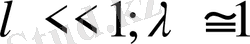-резонанс құбылысы

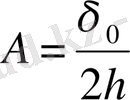Егер болса, демек, нүктеге күш әсер етпесе, онда 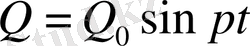гармониялық күші әсерінен мәжбүр тербелістің дифференциалдық теңдеуі түрде беріледі.

Оның шешімі :

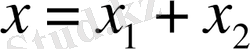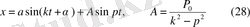
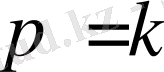болса

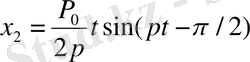
жүйе резонансқа шығады.

Дәріс 20. НҮКТЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ

Нүкте динамикасының есептерін шығару үшін нүкте қозғалыстарының дифференциалдық теңдеулерін интегралдау қажет. Бұл теңдеулерді интегралдау негізінде жеңіл емес. Сол үшін көп жағдайда нүктелер динамикасының жалпы теоремаларын пайдаланған жөн.

Онда есепті шығару үшін, теңдеулерді интегралдамай, аталмыш теоремалардың қорытынды өрнектерін пайдаланады. Ал теңдеулерді интегралдау әрекеттері теоремаларды дәлелдеуге орындалады.

Алдымен нүктенің қозғалыс мөлшерінің қозғалыс мөлшерінің өзгеруі туралы теоремасын қарастырамыз. Ол үшін бізге күш импульсы деген түсінік қажет.

§1. Күш импульсы

Белгілі уақыт аралығында нүктеге күш әсерін күш импульсы деп атаймыз. Оны 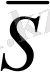деп белгілейміз. Күштің элементар импульсы күштің элементар dt уақытқа көбейтіндісін атаймыз:

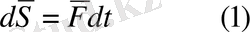
Күштің 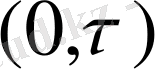шекті уақыт аралығындағы нүктеге әсерін шекті, 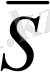импульсы деп атаймыз. Шекті импульс

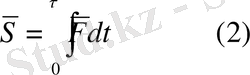
Егер күштің сан мәні мен бағыты тұрақты болса, онда

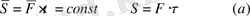
(2) -нің 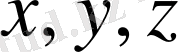координаттар өстеріне проекциялары

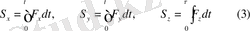
(3) -ті интегралдау үшін жалпы жағдайда нүктенің қозғалыс заңы

белгілі болуы қажет.

Импульстің өлшемі

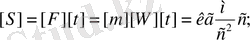
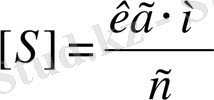немесе

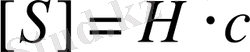
§2. Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема

Нүктенің қозғалыс мөлшері деп оның m массасымен 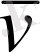жылдамдығының көбейтіндісіне тең 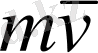векторлық шаманы атаймыз.

Қозғалыс мөлшері әр уақытта нүктенің

жылдамдығымен бағыттас, оның өлшемі

халықаралық СИ жүйесінде

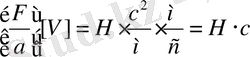
Техникалық бірлік өлшемінде

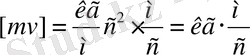
Нүктенің үдеуі 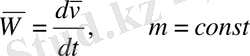екенін еске алсақ, динамиканың екінші заңы

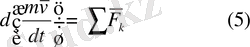болады.

(5) -нүктенің қозғалыс мөлшерінің өзгеруі туралы теоремасының дифференциалдық теңдеуінің түрін береді. Нүктенің қозғалыс мөлшерінің уақыт бойынша бірінші туындысы нүктеге тұскен күштердің геометриялық қосындысына тең. Егер 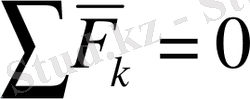болса, онда

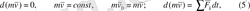
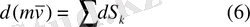
Бастапқы t=0 кезде нүктенің жылдамдығы 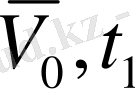кезде 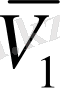болсын.

Онда (5) -тен:

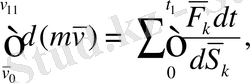
яғни

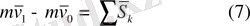
Нүктенің қозғалыс мөлешрінің шекті 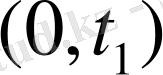уақыт аралығында өзгеруі нүктеге түскен күштер импульстарының геометриялық қосындысына тең. (7) теореманың интегралдық немесе шекті түрін береді.

Егер 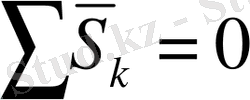болса, онда

Немесе

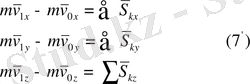
Егер 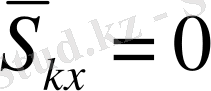болса,

(8) -бен (9) -ды нүктенің қозғалыс мөлшерінің сақталу заңы деп атайды.

§ 3. Нүктенің қозғалу мөлшері моменттің өзгеруі туралы теорема

Есеп шығарғандай кей жағдайларда қозғалыс мөлшерінің өзгеруі туралы теоремасының орнына нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теоремасын пайдаланған ыңғайлы.

О центрге немесе z өске қатысты нүктенің қозғалыс мөлшері моментін 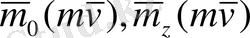деп белгілейік.

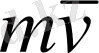вектор болғандықтан оның моменті күштің моменті сияқты анықталады.

Күш моменттері:

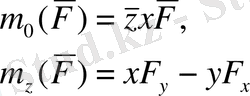
Нүктенің қозғалыс мөлшері 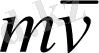моменттері:

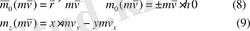
қозғалыс мөлшері моментінің z өске қатысты (9) өзгеруін қарастырайық.

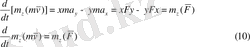
қозғалыс мөлшерінің центрге қатысты моментінің (8) өзгеруін қарастырайық

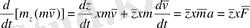
Егер

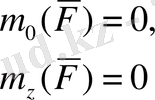онда

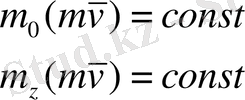(12)

(12) -ні нүктенің қозғалыс моментінің сақталу заңы деп атайды.

§ 4. Күш жұмысы

Күштің нүктеге орын ауыртыру әсерін күш жұмысы деп атаймыз. Оны А деп белгілейміз. Егер dS элементар орын ауыстыру аралығы болса, dA элементар жұмысты былай анықтаймыз.

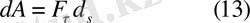
немесе

-оң жұмыс

- теріс жұмыс

- жұмыс орындалмайды.

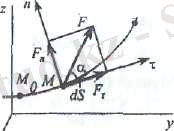
Күштің нормаль құраушысы 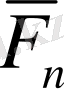жұмысқа әсер етпейді. Ол тек қозғалыс бағытын және реакция күшінің сан мәнінің өзгеруіне ғана әсер етеді. dS аз шама болса, және 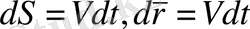екенін еске алсақ,

Демек,

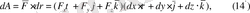
аяғында

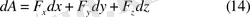
(14) -элементар жұмысының аналитикалық түрін береді.

Күш әсерінен нүктенің траектория бойымен 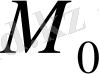орыннан 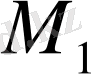орынға дейін орын ауыстырушы күштің сол орын ауыстырудағы шекті жұмысы деп аталады. Шекті жұмыс (14) - тен былай табылады.

Жұмыс өлшемі

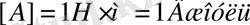
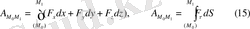
Уақыт бірлігі аралығында орындалатын жұмысты қуат деп атаймыз да, оны N деп белгілейміз.

Егер 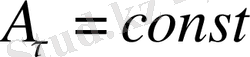, болса,

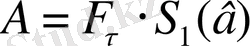
[A] = Нм = Джоуль - халықаралық СИ жүйесінде

[A] = Кгм - техникалық жүйеде.

Күш тұрақты болса, 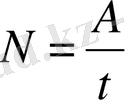. Айнымалы жағдайда

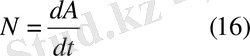
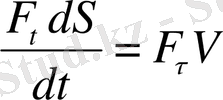[N] =Джоуль/с=1 вт.

§ 5. Жұмысты табу мысалдары

Ауырлық күш жұмысы.

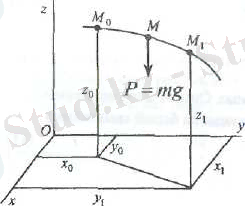Кеңістікте материялық нүкте

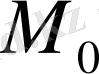
орнынан 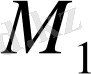орынға көшіп нүктеге

жалғыз күш әсер етеді:

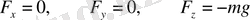
Онда

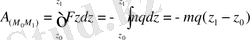Нәтижеде, күш жұмысы:

- тік орын ауыстыру.

(19) -дан байқайтынымыз ауырлық күш жұмысы траекториядан тәуелсіз. Мұндай күштерді потенциалды күштер деп атайды. Ауырлық күш потенциалдық күшке жатады.

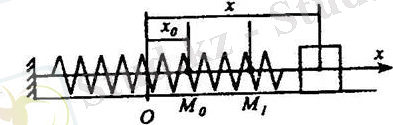2. Серпімділік күш жұмысы.

Нүктеге жалығыз серпімділік 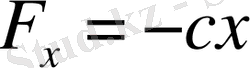күш түссін: ,

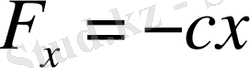Онда

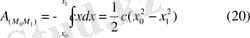
Серпімділік күш потенциалды күштерге жатады.

3. Үйкеліс күш жұмысы

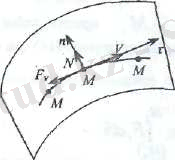
онда 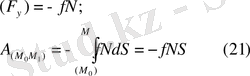Үйкеліс күші потенциалдық емес күштерге

жатады.

Дәріс 21. НҮКТЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ (ЖАЛҒАСЫ)

§ 6. Нүктенің кинетикалық энергиясының өзгеруі туралы теорема

Нүкте динамикасының екінші сипаттамасы - кинетикалық энергия. Нүктенің кинетикалық энергиясы деп, оның m массасы мен жылдамдығының квадратының көбейтіндісінің жартысын атаймыз. Оны Т деп белгілейміз. Демек,

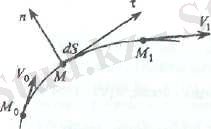
Материялық нүктенің М ₀ орыннан М ₁ орынға орын ауыстыруын қарастырайық; 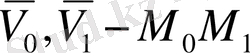нүктелердегі жылдамдықтары болсын. Динамиканың екінші заңының өсіне проекциясы

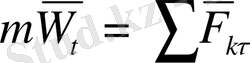
Мұнда 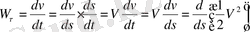_ 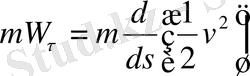Equation. 3

Олай болса, 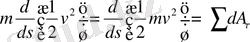немесе

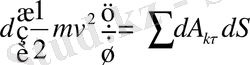
Яғни,

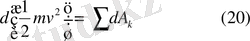
Бұл теореманың элементарлық немесе дифференциалдық түрі.

Теорема. Кинетикалық энергияның дифференциалы барлық нүктеге түскен күштердің элементарлық жұмыстарының қосындыларына тең.

(20) - теңдеудің екі жағынан интеграл алсақ,

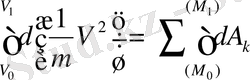
Онда

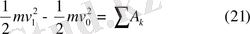
(21) -теореманың интегралдық түрін береді. Нүктенің М ₀ нүктеден М ₁ нүктеге көшкендегі кинетикалық энергиясының өзгеруі күштердің сол аралықтағы орын ауыстыру жұмыстарының қосындысына тең.

Мысал . Массасы m=0, 5 кг материялық нүкте жер бетінен бастапқы V=20м/с жылдамдықпен тасталғанда, М нүктеде оның жалдамдығы V=12 м/с болған.

Нүктенің М ₀ орыннан М орынға жеткенде

оның ауырлық күш жұмысы неге тең?

Шешімі:

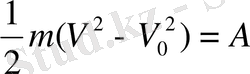
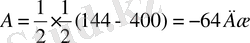
§7. Нүкте үшін Даламбер принципі

Нүкте динамикасының есептері Ньютонның негізгі заңынан туатын теңдеулермен және нүкте динамикасының жалпы теоремаларымен шешілетіні белгілі.

Сонымен қатар нүкте қозғалысын, “механика принциптері” дейтін жалпы жағдайларға сүйеніп қарастыруға болады.

Механиканың принциптері арқылы динамиканың есептері жеңіл, жинақтылау шешіледі.

Кез келген массасы m материялық нүктеге белсенді, - енжар күштер әсер етсін. Онда

немесе

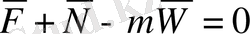
деп белгілесек,

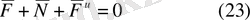
Мұнда 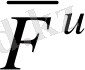күшті инерция деп атаймыз.

Демек, нүктеге түскен -белсенді, -енжар күштерге 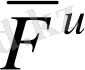-инерция қоссақ, нүкте тепе-теңдікте болады.

Бұл жалпы тұжырымды нүкте динамикасының Даламбер принципі деп атаймыз. (23) - теңдеуден Даламбер принципінің Ньютонның екінші заңына парапар екенін байқаймыз.

Даламбер принципі динамикасының негізгі принциптерінің бірі. Даламбер принципі динамиканың есептерін шығару үшін статиканың қарапайым әдістерін қолдануға мүмкіндік береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.