Тізбектер мен функциялардың шектері: монотонды тізбектер, Коши критерийі, Больцано-Вейерштрасс теоремасы және тамаша шектер


Жоспар:
- Нақты сандар тізбегі және оның шегі.
- Шегі бар тізбектердің қасиеттері.
- Ақырсыз кішкене және ақырсыз үлкен сандар.
- Монотонды тізбектер.
- Тізбектің жинақталуының Коши критерийі.
6. Функцияның лимитінің анықтамасы.
7. Шегі бар функциялардың қасиеттері
8. Тамаша шектер.
Больцано Вейерштрасс теоремасы.
1. Анықтама: Шексіз көп эмементке ие болған Х топтың элементтерін нөмерлеп оларды номерлері өсуі бойынша бір қатарға жазғандағы өрнекке тізбек дейіледі. Тізбектің элементері тұрақты сандар болса оған санды тізбек, ал айнымалы болса функцияналдық тізбек дейіледі. Тізбек
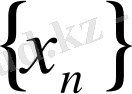 мен белгіленеді.
мен белгіленеді.
Мысалдар. 1)
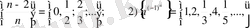

1, 2-сандық тізбектер, 3, 4, функционалдық тізбектер.
Анықтама: Егер бірар n>N
E
ден бастап тізбектің барлық мүшелері үшін
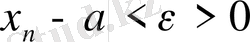 теңсіздігі орындалса онда а санына
теңсіздігі орындалса онда а санына
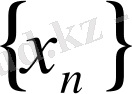 тізбектің шегі деп аталады. Ол
тізбектің шегі деп аталады. Ол
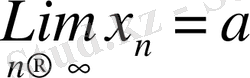 немесе
немесе
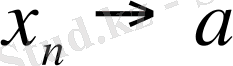 арқылы белгіленеді.
арқылы белгіленеді.
Мысал.
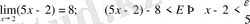 теңсіздігін қанағаттандырушы барлық Х тер үшін f(x) =5x-2 нің мәні
теңсіздігін қанағаттандырушы барлық Х тер үшін f(x) =5x-2 нің мәні
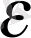 нен кіші болады.
нен кіші болады.
n артып барған сайын x тің мәндері a ның (a-E, a+E) маңайы ішінде a ға ұмтылады.
2. Шегі бар тізбектердің қасиеттері.
- Егертізбектің шегі бар болса, онда ол шек жалғыз.
- Егертізбегі жинақты болса, онда ол тізбек шенелген.
- Егер
- Егерболыпболса ондаEquation. 3 болады.
3. Шегі бар тізбектерге арифметикалық амалдырды қолдану.
Егер
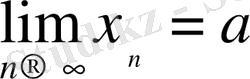 , және
, және
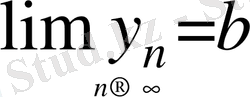 болса онда
болса онда
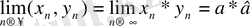
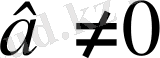 болғанда
болғанда
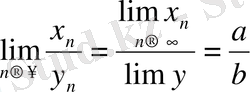 болады.
болады.
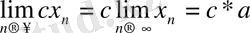
- Ақырсыз кішкене және ақырсыз үлкен сандар.
Анықтама.
Шегі х→х
0
де нөлге ұмтылушы α(х) ақырсыз кішкене шама деп аталады.
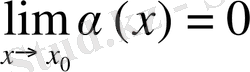
Мысал.
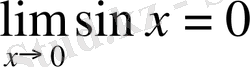 ;
;
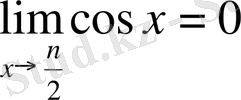 ;
;
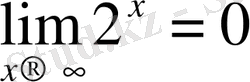 ;
;
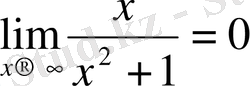 ;
;
Ескерту. Ақырсыз кіші шама әрқандай тұрақты кіші саннанда кіші болады.
Анықтама.
Шегі
 шексіздікке ұмтылғанда
шексіздікке ұмтылғанда
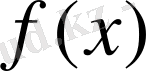 шексіз үлкен шама деп аталады. Немесе әрқандай үлкен санан да үлкен болған шамаға ақырсыз үлкен шама делінеді.
шексіз үлкен шама деп аталады. Немесе әрқандай үлкен санан да үлкен болған шамаға ақырсыз үлкен шама делінеді.
Мысал.
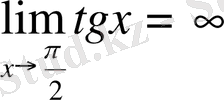 ;
;
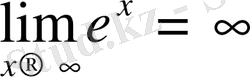 ;
;
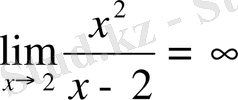
Ақырсыз кіші шамалардың негізгі қасиеттері туралы теоремалар:
- лимиті а-ға тең болып, шексіз кіші шама болса ондатеңдігі орындалады. Мысал,
2) Егер d(x) шексіз кіші шама болса онда 1/d(x) шексіз үлкен
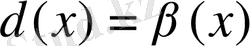 ақырсыз кіші шама
ақырсыз кіші шама
3) Егер ақырсыз кіші шаманың қосындысыда шексіз кіші шама болады шекті сандағы ақырсыз кіші шамалардың қосындысы шексіз кіші шама болады .
4) Егер if(x) <m болып d(x) ақырсыз кіші шама болса онда f(x) шексіз кіші шама болады.
5) d(x) ақырсыз кіші шама болып
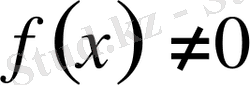 болса
болса
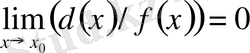 болады.
болады.
Функция лимитінің анықтамсы.
Анықтама: Кез-келген кіші сан Е>0 үшін у=f(x) функцияның анықталу аймағында сондай бір кіші сан

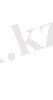 табылып
табылып
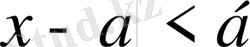 қанағаттандыратын х тер үшін
қанағаттандыратын х тер үшін
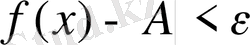 шарты орындалса А-ға f(x) функцияның
шарты орындалса А-ға f(x) функцияның
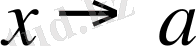 дағы лимиті дейіледі. Ол былай жазылады.
дағы лимиті дейіледі. Ол былай жазылады.
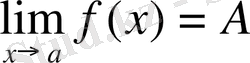
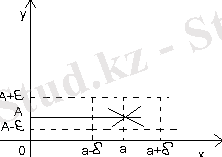
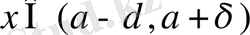 болғанда f(x) функцияның мәні
болғанда f(x) функцияның мәні
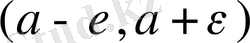 аралығында болып
аралығында болып
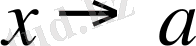 да f(x) функця графигі (а, А) нүктеден өтеді.
да f(x) функця графигі (а, А) нүктеден өтеді.
- Шегі бар функциялардың қасиеттері.
1) . f(x) функцияның
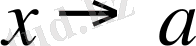 дағы шегі бар болса онда ол шек жалғыз.
дағы шегі бар болса онда ол шек жалғыз.
2) .
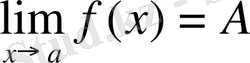 болса
болса
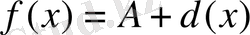 деп жазса болады. Бүл жерде
деп жазса болады. Бүл жерде
 (x)
(x)
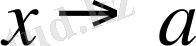 дағы шексіз кіші шама
дағы шексіз кіші шама
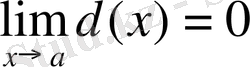
3) . Егерде x=a ның маңайында
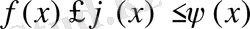 шарты орындалып,
шарты орындалып,
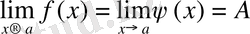 болса онда
болса онда
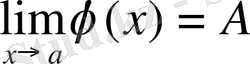 болады.
болады.
4) . Тұрақты санды функция шегінің алдана шығаруға болады.
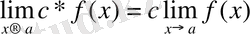
5) . Егер
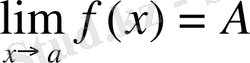 ,
,
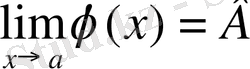 болып А және В const болса онда.
болып А және В const болса онда.
А) .
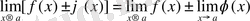
Алгебралық жиындының лимиті қосылушылар лимиттерінің алгебралық жиындысына тең.
Б) .
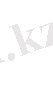
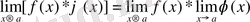
Көбейтіндінің лимиті көбейушілер лимиттерінің көбейтіндісіне тең.
Тамаша лимиттер.
А) . Бірінші тамаша лимит.
Теорема
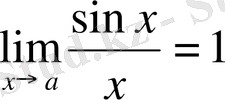
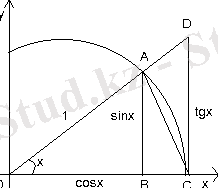
Дәлелі: 0А=1 сызбадан десек АВ=sinx 0В=cosx және CD=tgx болады.

Сонымен бірге
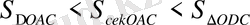 (1)
(1)
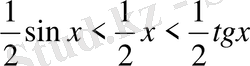 (2)
(2)
(2) ні
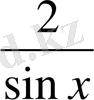 ке көбейтсек онда
ке көбейтсек онда
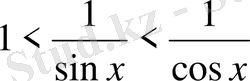 болады немесе
болады немесе
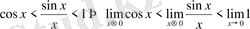
Лимиті бар функциялардың 4-ші қасиетінен
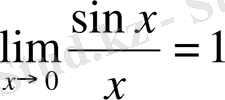 келісіп шығарады.
келісіп шығарады.
Мысалдар:
1)
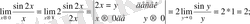
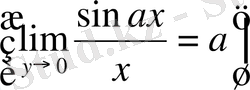
2)
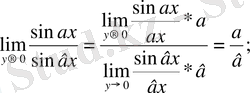
3)
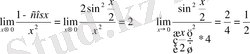
Б) . Екінші тамаша лимит.
Теорема:
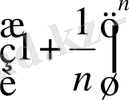 сан тізбегінің шегі
сан тізбегінің шегі
 да 2 мен 3 арасындағы санға ұмтылады.
да 2 мен 3 арасындағы санға ұмтылады.
Дәлелі:
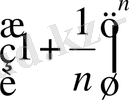 ді Ньютон биномы
ді Ньютон биномы
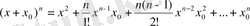 бойынша жіктейік. Бұл жерде x=1
бойынша жіктейік. Бұл жерде x=1
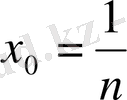 болғандығы үшін
болғандығы үшін
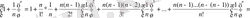
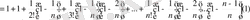
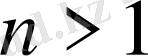 болғанда (1) -дің барлық мүшелері оң таңбалы және олар
болғанда (1) -дің барлық мүшелері оң таңбалы және олар
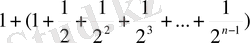 (2) сан тізбегі сәйкес мүшелерінен үлкен емес, ал (2) нің жақша ішіндегі бөлігі
(2) сан тізбегі сәйкес мүшелерінен үлкен емес, ал (2) нің жақша ішіндегі бөлігі
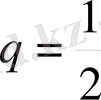 болған кемейуіші геометриялық прогрессия
болған кемейуіші геометриялық прогрессия
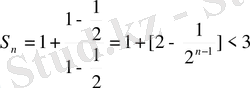 . Сондықтан
. Сондықтан
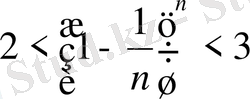 теңсіздігі орындалады. Яғни
теңсіздігі орындалады. Яғни
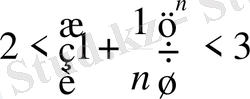 ті аламыз.
ті аламыз.
Анықтама:
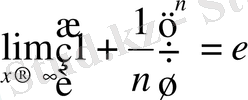 е иррационал сан болып ол 2, 7182818284 . . . ке тең.
е иррационал сан болып ол 2, 7182818284 . . . ке тең.
Теорема:
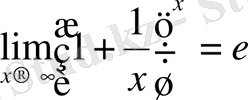
Дәлелі.
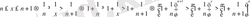
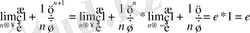
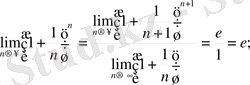
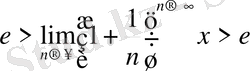 ден
ден
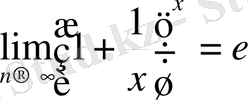 келіп шығады.
келіп шығады.
Мысалдар:
1)
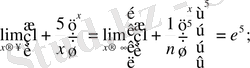
2)
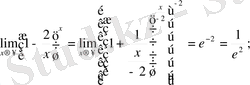
Әдебиеттер:
негізгі:
1. Темірғалиев Н. ” Математикалық анализ, І т, Алматы 1987
2. Фихтенгольң г. т “Математикалық анализ негіздері, ” І т Москва 2003ж
қосымша:
- Н. С. Пискунов, Дифференциальное и интегральное исчесления І, ІІ том, Москва, 1988 г.
- В. П. Минорский, «Сборник задач по высшей матеамтике», Москва, «Наука» 1987 г.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz