Геометриялық фигуралар

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Пирамида. Табаны деп аталатын кѳпбұрышты және бүйір жақтары деп аталатын үшбұрыштармен шектелген көпжақты пирамида деп атайды. Егер пирамиданың табаны n бұрышты фигура болса, онда оны n бұрышты пирамида дейді. Пирамиданың табаны бесбұрыш ABCDE, сондықтан оны бесбұрышты пирамида дейді. Бүйір жақтарының ортақ нүктесі S пирамиданың төбесі болады. Пирамидаларды дұрыс және дұрыс емес деп екі топқа бөлуге болады. Дұрыс пирамиданың табаны дұрыс көпбұрыш болады және оның төбесінен табанына түсірілгсн перпендикуляр табанындағы көпбүрыштың центріне түседі. Горизонталь проекция жазықтығында тұрған дұрыс үшбұрышты пирамиданың сызбасы кескінделгсн. Алдымен пирамиданың горизонталь проекциясын тұрғызып алады. Пирамиданың табаны горизонталь проекция жазықтығында жатқандықтан, бүрмаланбай нақты шамасына проекцияланады. Абсцисса осін қалауымызша орналастырып, онымен қиылыспайтын және төмен орналасқан шеңбер жүргіземіз. Шеңбердің центрі S 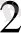Equation. 3 пирамида тѳбесінің горизонталь проекциясын береді. S 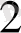Equation. 3 нүктесі арқылы вертикаль түзу жүргізіп, оның шеңбермен қиылысу нүктесін пирамида төбелерінің бірінің горизонталь проекциясы ретінде қабылдаймыз. Ол нүктсні A 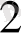Equation. 3 деп белгілейік. Бір төбссі A 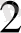Equation. 3 нүктесі болатын шеңберге іштсй дұрыс үшбүрыш сызамыз. Бұл үшбұрыштың бір қабырғасы ВС фронталь проекция жазықтығына параллель. Табылған A 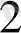Equation. 3, В 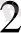Equation. 3 және C 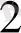Equation. 3 нүктелерін өзара жәнс S 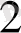Equation. 3 нүктесімсн қоссақ, пирамиданың горизонталь проекциясы шығады. А Equation. 3, B Equation. 3 жәнс C ₂ нүктелері арқылы вертикаль байланыс сызықтарын 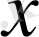осіне дейін жүргізіп, A ₁ , В ₁ және C ₁ нүктелерін аламыз. Пирамиданың биіктігіне тең A ₁ S ₁ кесіндісін салып, S ₁ нүктесін табамыз. Табылган A ₁ , B ₁ , C ₁ және S ₁ нүктелерін кесінділермен қосу нәтижесіндс пирамиданың, фронталь проекциясын шығарып аламыз. Профиль проекцияны тұрғызу үшін қалауымызша z осін жүргізіп (оны вертикаль орналастыру қажст), S, А, В жәнс С нүктелерінің профиль проекцияларын - S ₃ , A ₃ , B ₃ және C ₃ нүктелерін саламыз. Пирамиданың бүйір жағы - SBC үшбұрышы профиль проекциялаушы фигура болғандықтан, оның профиль проекциясы кесіндіге кескінделген, ал қыры SA профиль орналасқан кесінді болғандықтан, ₃ жазықтығына нақты шамасына проекцияланған үшбұрышты дұрыс пирамиданың тік бұрышты изометриясы көрсетілген.

Дұрыс үш бұрышты пирамиданың моделін картоннан немесе қатты қағаздан жасауға болады. Ол үшін пирамиданың жазбасын салу керек. Көп жақты беттің жазбасы жазықтыққа бір-біріне түйістіре салған жақтардың нақты шамаларынан тұрады. Біздер қарастырып отырган мысалда алдымен пирамиданың табанын салып алған дүрыс. A ₂ B ₂ C ₂ үшбұрышына тең A ₀ B ₀ C ₀ үшбұрышын саламыз. Осы үшбұрыштың қабырғаларына бірдей тең бүйірлі A ₀ S ₀ B ₀ , B ₀ S ₀ C ₀ және C ₀ SoA ₀ үшбұрыштарын тұрғызамыз. Модель жасау үшін жазбаны қиып алып, қос нүктелі үзілме сызықтар бойынша бүгіп, S ₀ нүктелерін бір нүктеге біріктіру керек. Содан кейін пирамиданың бүйір қырларын желімдеу керек.

Дұрыс бес бұрышты пирамиданың проекциялары көрсетілген. Мұнда да алдымен горизонталь проекция салынады. Шеңберге іштей дұрыс бесбұрыш тұрғызылады. Пирамиданың горизонталь проекциясы бойынша фронталь проекциясы, ал фронталь және горизонталь проекциялары бойынша профиль проекциясы салынады. SABCDE бес бұрышты пирамиданың қиғаш бұрышты фронталь диметриясы сызылған.

Призма. Табандары деп аталатын екі жағы параллель және тең кѳпбұрыштар, ал қалган бүйір жақтары параллелограмдар болатып

көпжақты призма деп атайды. Егер табаны п бүрышты фигура болса, онда призма n бұрышты призма деп аталады. Призмаларды тік және келбеу призмалар деп екі топқа бөледі. Тік призманың жақтары тік төртбұрыштар болады және табандарымен 90° бұрыш жасайды. Табаны дұрыс n бұрыш болатын тік призманы дұрыс n бұрышты призма дейді. Дұрыс алты бұрыш-ты призманың сызбасы, ал оның фронталь қиғаш бұрышты диметриясы көрсетілген. Призманы фронталь проекцияда оның үш жағы көрінетіндей етіп орналастырады, оның себебі кейінірек айтылады. Алдымен горизонталь проекциясын салып алған дұрыс. Призманың табандары горизонталь орналасқан, сондықтан олар ₂ жазықтыгына нақты шамасына проекцияланған. Призманың алты бүйір жағы - горизонталь проекция жазықтығына перпендикуляр орналасқан тік төртбұрыштар. Олар-дың екеуі фронталь проекция жазықтығына параллель. Бүйір қырлары - горизонталь проекциялаушы кесінділер, ал табан қырлары - горизонталь орналасқан кесінділер үш бұрышты көлбеу призманың фронталь, горизонталь және профиль проекциялары салынған.

Цилиндр. Цилиндр туралы жоғарыда айтылған. Математика курсында цилиндрді тік тѳртбұрыш өзінің бір қабырғасынан айналғанда шығатын айналу денесі деп түсіндіреді. Тік төртбұрыштың қозғалмайтын қабырғасын цилиндрдін осі деп атайды, ал оған қарама-қарсы қабырғасы - жасаушысы цилиндрдің бүйір бетін және қалған екі қабырғасы цилиндрдің табандары болатын бірдсй екі дөңгелекті сызып шығады. Горизонталь проекция жа-зықтыгында тұрған цилиндрдің сызбасы және тік бұрышты изометриясы сызылған. Цилиндрдің фронталь және профиль проекциялары - тең тік төртбұрыштар, ал горизонталь проекциясы шеңбер болатынын көреміз. Айналу цилиндрінің осі табан жазықтықтарына перпендикуляр. Цилиндрдің бетінде жататын оның осіне параллель кесінді жүргізуге болады. Осындай кесінділердің бірі AB көрсетілген. Осындай кесіндіні, мысалы AB кесіндісін, цилиндрдің жасаушысы деп атайды.

Оның себебі AB кесіндісін осьтен айналдырса, онда ол кесінді цилиндрдің бүйір бетің жасайды. Цилиндрді картоннан жасап алуға болады. Ол үтін оның жазбасын салу керек. Цилиндрдің жазбасы келтірілген. Жазба төртбұрыштан және екі дөңгелектен тұрады. Дөңгелектер - цилиңдрдің табаңдары, ал тік төртбұрыш - оның бүйір бетінің жазбасы. Тік төртбұрыштың биіктігі цилиндрдің биіктігіне тең, ал ұзындығы оның табанындағы дөңгелек шеңберінің ұзындыгына тең. Шеңбердің ұзындығы с болсын, ал диаметрі d болсын. Олардың қатынасың гректің («пи» деп

оқылады) әрпімен бслгілейді. Сонда 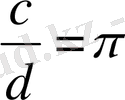. Осыдан ал

= 3, 14. Жоғарыда қарастырылған цилиндрді тік цилиндр дейді.

Жасаушылары табан жазықтықтарына көлбеу болатын цилиндрді көлбеу цилиндр деп атайды. Келбеу цилиндрдің табандарындағы дөңгелектердің центрлерін қосатын түзу (цилиндрдің осі) оның табан жазықтықтарына перпендикуляр болмайтындыгын байқау қиын емсс, көлбеу цилиндрдің сыз-басы көрсетілген.

Конус . Тік бұрышты үшбұрышты катеттерінің біреуінен айналдырғанда шығатын айналу денесін конус дейді. Тік бұрышты үшбұрыштың қозғалмайтын катеті конустың осі, гипотенуза жасаушысы деп аталады, ал екінші катет конустың табаны болатын дөңгелекті жасайды. Айналу конусының сызбасы, ал аксонометриясы кескінделген. S нүктесі конустың тѳбесі деп аталады. Сонда конустың фронталь және профиль проекциялары тең бүйірлі үшбұрыштар, ал горизонталь проекциясы табанына тең дөңгелек болады. Конустың төбесі жазықтығына өзінің горизонталь проекциясы болатын доңгелектің центріне проекцияланады. Конустың аксонометриясын салу үшін аксонометриялық осьтер жүргізіп, табанының центрі - O' нүктесі координаттары бойышна салынады. Одан кейін конустың табанындағы шеңбердің кескіні болатын овал сызылады, Конус төбесінің аксонометриясы - S' нүктесі координатары бойынша салынады. S' нүктесінен жүргізіледі Конусты картоннан жасау үшін оның жазбасын салуды қарастыралық. Қалауыңызша So нүктесін алып, центрі осы S ₀ нүктесі болатын, радиусы конус жасаушысының ұзындығына тең шеңбер доғасын жүргізеді. Доғаның бір үшын A ₀ деп белгілейік. Доғаның бойына A ₀ нүктесінен бастап шенбердің (конустып, табанындағы) ұзындығын салу керек. Бұл арада жуықтап салу әдісін пайдаланған тиімді. Шеңберді тең 12 бѳлікке (оданда көп тең бөліктерге) бөледі. А ₂ B ₂ - шеңбердің 1/12 бөлігі болсын. A ₂ B ₂ кесіндісін өлшеуішпен (шеңберсызармен) өлшеп алып, доғаның бойына A ₀ нүктесінсн бастап 12 рет салады. Ең соңғы нүктені және A ₀ нүктесін S ₀ нүктесімен кесінді арқылы қосады. Сонда конустың бүйір бетінің жазбасы шығады. Оның толық бетінің жазбасын алу үшін, бүйір бетінің жазбасына тақап конустың табанын салса болады.

Егер төбссі мен табанының центрін қосатын түзу оның табанына перпендикуляр болмаса, конусты көлбеу конус дейді.

Шар. Доңгелекті диаметрлсріпің біреуінен айналдырғанда пайда болатын денені шар деп атайды. Шардың бетін сфера дейді, оның проекциялары өзара тең шеңберлср болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.