Сызықты емес теңдеулерді шешудің сандық әдістері


М А З М Ұ Н Ы
І Кіріспе
1. 1 Сызықты емес теңдеулерді шешудің сандық әдістері
1. 2 Жай итерация және қарапайым итерация әдістері
Итерация әдісі. Теңдеуді итерациялық түрге келтіру
Жүйені итерациялық түрге келтіру
Хорда әдісі
Жанама әдісі
Кесіндіні қақ бөлу әдісі
Сызықты емес теңдеулер жүйесін шешудің сандық әдістері
Глосарий
Әдебиеттер тізімі
Сызықты емес теңдеулерді шешудің сандық әдістері
Сандық әдістердің бір бөлімі «бір өлшемді сызықты емес теңдеулер» болып табылады. Физикалық және басқа да құбылыстардың теңдеумен сипатталатыны белгілі. Сол теңдеуді классикалық математикалық формуламен шешу мүмкін емес жағдайлар бар. Бұл уақытта практикада сандық әдістерге жататын әдістермен шешілетінін дәлелдеу керек. Әрине ең алдымен құрылған теңдеудің қай аралықта анықталғандығын, үзіліссіздігін, түбірінің барлығын, оның жалғыздығын дәлелдейтін аргументтерді бақылау керек. Осы этаптан өткеннен кейін ғана есепті осы теңдеуге қолдануға келетін алгоритм көмегімен шығаруға болады.
Сызықты емес теңдеулер екі түрлі:
Алгебралық;
Трансцендентті;
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.
Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функцялары бар теңдеуді айтады.
Сызықты емес теңдеуді сандық шешу екі тәсілден ([1] қараңыз) тұрады.
1 Тура тәсіл- есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару;
2 Итерациялық тәсіл- есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару;
Тура тәсілмен шығарылған есептер дәл мәнді береді. Ал итерациялық тәсілмен шешілген есептер есептің жуық мәнін береді . Мұның ішінде итерациялық әдістер сандық әдіске жатады.
Бір өлшемді сызықты емес теңдеуді шешудің келесі әдістері бар.
1 Кесіндіні қақ бөлу - дихотомия әдісі деп аталады;
2 Хорда әдісі;
3 Жанама әдісі;
4 Жәй итерация әдісі;
F(x) =0 (2. 1)
Бірөлшемді сызықты емес теңдеу берілген. Мұндағы F(x) функциясы [a, b] кесіндісінде анықталған және үзіліссіз болсын.
Теорема1. 1: [а, в] аралығында анықталған, үзіліссіз F(x) функциясының екі шеткі нүктелердегі мәндерінің таңбалары әр түрлі болса, яғни мына шарт орындалса f(a) *f(b) <0, онда осы аралықта (2. 1) -теңдеудің түбірі бар және жалғыз болады.
Практикада кейде теореманың орындалуын функцияның мәндер кестесін құру арқылы да анықтайды. Функцияның анықталу облысы бойынша а нүктесін беріп, ол нүктедегі функция мәнін анықтайды, сосын һ қадаммен келесі нүктеге жылжып, сол нүктедегі функция мәнін анықтайды, сол сияқты бірнеше нүктедегі функция мәндерін анықтап, таңбасын салыстырады. Егер көрші нүктелерде функция әр түрлі таңба қабылдаса, сол аралықта жалғыз түбірі жатыр деп айтады.
1-мысал:
Берілген теңдеудің түбірін анықтау:
Теңдеудің түбірі жатқан аралықты аналитикалық тәсілмен табамыз: ол үшін функция туындысын тауып, оны нөлге теңестіру арқылы экстремумдарын анықтаймыз:, экстремумы: х1=Ln10=2, 3;
Экстремум нүктелеріндегі функция таңбасының 1-кестесін толтырамыз.
1-кесте-функциясының таңбасын анықтау
Функция таңбасының ауысуы (; 2, 3] және [2, 3; ) аралығында байқалды. Яғни осы аралықта теңдеудің түбірі бар.
Енді графиктік әдісті қарастырайық. Ол үшін теңдеуді мына түрлерге жіктейміз, себебі функция күрделі, трансцендентті, бірден графигін құруға болмайды:. Екі функцияның графигін саламыз, екеуінің қиылысқан нүктесі теңдеудің түбірі болып табылады (1-сурет) . Қиылысу нүктелерінің аймақтарын анықтаймыз.
1-сурет-функцияларының графиктері
Бірінші түбірі [0, 1] аралығында, ал екінші түбірі [2, 6] аралығында жататыны суретте көрініп тұр. Енді осы аралықтағы қай нүкте (2. 1) -ші теңдеуді қанағаттандыратынын анықтаймыз.
f(x) =0 (1) теңдеуі берілсін.
Әр түрлі ғылым мен техника салаларында жиі кездесетін, ертеден келе жатқан математикалық есеп.
Мұндағы f(x) функциясы қандайда бір ақырлы немесе ақырсыз a<x<b аралығында анықталған және үзіліссіз
функция. f(x) функциясын нольге айналдыратын, қандайда бірмәні (1) теңдеуінің түбірі деп аталады.
Сызықтық емес теңдеулердің түрлері:
1) квадрат теңдеу:(Виетта түбірлері мен анықталады)
2) кубтық теңдеу:(Кардано әдісімен анықталады)
3) төртінші дәрежелі теңдеу:(Феррари әдісімен анықталады. )
Француз математигі Галуа бесінші дәрежелі теңдеуден бастап f(x) =0 алгебралық теңдеулерді дәл шешу мүмкін
еместігін дәлелдеген. Сондықтан сызықтық емес теңдеулер түбірлерін жуықтап есептеу мәселелерін қарастыруға
тура келеді.
Бір айнымалы сызықтық емес теңдеу алгебралық және транцендентті теңдеу болып екіге бөлінеді.
а) х - айнымалының бүтін дәрежелі қосылғыштарынан тұратын теңдеу - алгебралық теңдеу деп аталады.
Алгебралық теңдеудің жалпы түрі:
б) Тригонометриялық немесе басқа арнайы функцияларды қамтитын теңдеу - транцендент теңдеу деп аталады.
Мысалы:
;
Әдетте, теңдеулердің нақты түбірлерін жуықтап табуды келесі сатылардан тұрады.
1. Түбірлерді жекешелеу
2. Түбірлерді дәлдеу
Кесіндіні қақ бөлу әдісі
(2. 1) - теңдеуді кесіндіні қақ бөлу әдісімен шешу алгаритмі келесі қадамнан тұрады.
(2. 1) -ші теңдеудің түбірі жатқан аралығын анықтау және осы аралықта түбірдің жалғыздығын тексеру. Яғни x осі бойында бірдей қашықтықта жатқан нүктелердегі функцияның мәндерін есептеміз, және егер екі шеткі нүктеде немесе екі көрші нүктеде функция мәндерінің таңбалары әр түрлі болса, онда сол аралықта түбір бар деп есептеу
Осы аралықты қаққа бөлу және ол нүктенің мәнін
Xорт=(Xn+1+Xn) \2 (2. 2)
формуласымен анықтау.
/Xn+1-Xn/<e шарты арқылы қарастырылып отырған аралықтан шығып кетпеуді бақылаймыз.
XОРТ нүктесіндегі функция мәнін F(XОРТ) есептеу.
Егер оның таңбасы F(Xn) функциясының таңбасымен бірдей болса, Xn нүктесінің орнына XОРТ нүктесін қарастырамыз.
Ал егер F(XОРТ) функциясының таңбасы F(Xn+1) функциясының таңбасымен бірдей болса, Xn+1 нүктесінің орнына ХОРТ нүктесін қарастырамыз.
Шыққан аралықтар [Xn,, Хорт] U [Xорт, Xn+1] белгіленеді. және алдыңғы шарттарға байланысты екі аралықтың біреуін тағы қаққа бөлу арқылы ізделінді нүктеге біртіндеп жақындаймыз. Яғни мына шарттар тексеріледі: F(Xn+1) *F(Xорт) <0 шарты орындалса [Xорт, Xn+1] аралығы қаққа бөлінеді де шыққан нүкте мәні, XОРТ2=XОРТ+Xn+1/2 формуласымен есептеледі. F(Xn) *F(ХОРТ) <0 шарты орындалса [Xn, Xорт] аралығы қаққа бөлініп, табылған нүкте XОРТ2=XОРТ+ Xn/2 формуласымен есептеледі.
Осы процесті іздеп отырған х нүктесіне жеткенге дейін жалғастырып, XОРТ, XОРТ2, XОРТ3, …, XОРТN тізбегін құрамыз. Мына шарт орындалатын уақытта /XОРТN - XОРТN-1/<E іздеу процесін тоқтатамыз да XОРТN нүктесін (2. 1) -ші теңдеуді қанағаттандыратын х дәл түбірге жуық мән деп қабылдаймыз.
Программасы
Program bisekzia;
Label 1;
Var a, b, e, c:real;
Function f(x:real) :real;
Begin
F:=exp(x) -10*x;
End;
Begin
Writeln(‘аралықты және епсилонды енгізіңіз’) ;
Read(a, b, e) ;
1: c:=(a+b) /2;
if abs(b-a) <e then
write(‘x=’, c)
else
begin
if f(c ) *f(a) <0 then b:=c else a:=c;
goto 1;
end;
writeln(exp(c ) -10*c) ;
end.
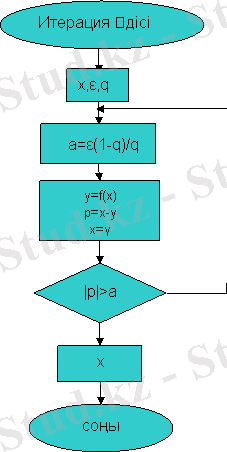
Жай итерация әдісі
Бұл әдісті қолдану үшін (2. 1) -ші теңдеудің сызықты мүшесі айшықталып мына түрге келтіру керек:
(2. 3)
Сосын теңдеудің түбіріне кез келген Х0 бастапқы жуықтау беріпk=1, 2, … формуласымен х1, х2, …, хn нүктелер тізбегін құрамыз. Бұл тізбек x=z түбіріне жинақталуы керек. Егер limXk=z болса, онда z нүктесітеңдеуінің түбірі бола алады. Итерация әдісінің жинақтылық шартыжәне бастапқы жуықтау кез келген болады. Итерациялық процесс берілген дәлдікке жетуі үшіншарты орындалуы керек.
Итерациялық тізбектің жинақтылығы теореманың ([1] қараңыз) шарттарымен де тексерілуі керек:
Теорема1. 2. :
теңдеуінің [a, b] аралығында жалғыз түбірі бар және келесі шарттар орындалсын:
1функциясы [a, b] аралығында анықталған және дифференциалданады;
2үшін;
3 барлықүшінболатындай q саны табылсын,
онда, (k=1, 2, …) итерациялық тізбегікез келген бастапқы жуықтауда жинақталады.
Теңдеуді итерациялық түрге келтіру
(2. 1) -теңдеуді (2. 3) -ші итерациялық түрге келтіру әртүрлі тәсілдермен орындалады. Қай тәсілмен итерациялық түрге келтірілсе де жоғарыдағы теореманың шарттары орындалуы керек. Практикада көрінгендей, теореманың 3) -ші шартының орындалуы күрделірек, сондықтан төмендегі тәсілдердің бірін қолдануға болады:
1 (2. 1) -теңдеудітүріне келтірейік, мұндағы m=const нөлден өзгеше. Бұл уақыттадеуге болады. Оны дифференциалдасақ:. Теореманың 3) -ші шарты орындалуы үшінүшіншарты орындалатындай етіп m-ді таңдап алу керек.
2 (2. 1) -теңдеу (2. 3) -ші түрге келтірілген, бірақ теореманың 3) -ші шарты орындалмай тұрса, онда y=функциясының орнына x=g(y) функциясын қарастыруға болады. Мұндағы g(y) функциясыфункциясының кері функциясы. Енді y=g(y) теңдеуін шешетін боламыз. Немес ескі белгілеулер бойынша x=g(x) теңдеуін шешеміз деген сөз. Кері функциялардың туындыларының қасиеттері бойынша.
2 - мысал
теңдеуінің түбірін қарапайым итерация әдісімен табу керек болсын. Теңдеуді итерациялық түрге келтіреміз:
. Ал және барлық х нүктелері үшін
. Яғни q=0, 1 деп алып, бастапқы жуықтауды х0=0 десекшарты орындалғанша итерациялық процесті құрамыз: х0=0:;, т. с. с. Түбір мәні х6=0, 111833, итерация саны 5-ке тең.
Хорда әдісі
Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез жинақталады.
Алгоритмі:
хn, xn+1 аралығында f (x) және f (xn+1) функцияларының таңбасы бір біріне қарама-қарсы және түбірі бар болсын.
Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен қиылысқан нүктесін мына формуламен анықтаймыз.
(2. 4)
Егер f(a) >0 шарты орындалса, а нүктесі тұрақты болады даформуласымен есептеледі
Егер f(b) >0 шарты орындалса, b нүктесі тұрақты болады даформуласымен есептеледі
х* нүктесіндегі функция мәнін F(x*) -ны есептеу. Оның таңбасын екі шеткі нүктедегі функцияның таңбасымен салыстырылады. Егер f (xn) және f(x*) функциясының таңбасы бірдей болса, онда хорданы xn+1 және x* нүктесі арқылы жүргізіледі. Оның мәнін (2. 4) формуламен табады. Егер f(xn+1) мен f(x*) функцияның таңбалары бірдей болса, онда хорданы xn және x* нүктесі арқылы жүргізіледі. Шыққан нүктенің мәні (2. 4) формуламен есептелінеді.
x* нүктедегі мәнін есептеп, мәні нөлге жуық болса, онда x* нүктесі (2. 1) теңдеудің түбірі деп аталады. Егер нөлге жуық болмаса, онда процесс жалғасады.
Алдындағы мысал үшін программасы келесідей болады:
Хордалар әдісінде
нүктесі ретінде еркін нүкте емес, осініңжәненүктелері арқылы жүргізілген хордамен қиылысу нүктелері
алынады. нүктесін табу үшінхордасының теңдеуін жазайық:
(19)
деп, сәйкес мәндерді табамыз
(20)
f(x) =0 (1) теңдеуінің [a, b] кесіндісіндегі түбірін анықтау керек. [a, b] кесіндісіндегі f'(x) >0 және f"(x) >0. Яғни:
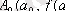 және
және
 нүктелері арқылы
нүктелері арқылы
 хордасын жүргіземіз.
хордасын жүргіземіз.
у
 B0
B0



 х
х
 A1
A1
 A0
A0


 екі нүкте арқылы жүргізілген түзудің теңдеуін,
екі нүкте арқылы жүргізілген түзудің теңдеуін,
 хордасы үшін жазайық:
хордасы үшін жазайық:
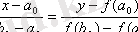 (2)
(2)
(2) - де
 болғанда
болғанда
 десек:
десек:
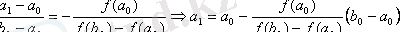

Сонымен f(x) функциясының графигінің бойынан
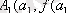 нүктесі анықталады. Енді осы А1 және В0 нүктелері арқылы хорда жүргізейік, яғни ол
нүктесі анықталады. Енді осы А1 және В0 нүктелері арқылы хорда жүргізейік, яғни ол
 хордасы.
хордасы.
Оның теңдеуі:
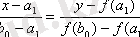 (3)
(3)
l2 хордасының Ох қиылысу нүктесі:
 у=0;
у=0;
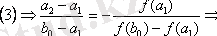
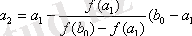
Мұндағы:
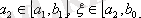
Осындай үрдісті әрі қарай жалғастыра отырып,
 (5) шексіз тізбек аламыз. Оның кез - келген мүшесі:
(5) шексіз тізбек аламыз. Оның кез - келген мүшесі:
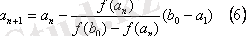
формуласымен анықталады. Мұнда:
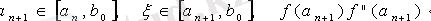
Тұжырымдама: Сонымен, жоғарыдағы үрдістің нәтижесінде алынған
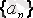 тізбегі жинақты және оның шегі:
тізбегі жинақты және оның шегі:
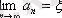 болады.
болады.
Шындығында да,
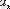 тізбегі монотонды өспелі (кемімелі), жоғарыдан (төменнен) шектелген тізбек, олай болса, оның шегі болады, яғни:
тізбегі монотонды өспелі (кемімелі), жоғарыдан (төменнен) шектелген тізбек, олай болса, оның шегі болады, яғни:
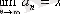 және
және
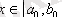
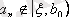 олай болса
олай болса
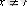 (5)
(5)
 , шекке көшсек:
, шекке көшсек:
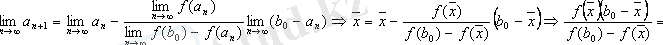
Мұнда
 болған,
болған,
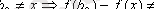 , олай болса,
, олай болса,
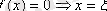
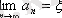
тұжырым дәлелденді.
Блок сызбасы:




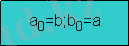
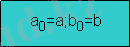

























f(x) =0 (1) теңдеуі берілген. Түрлендірулер арқылы (1) теңдеуін оған эквивалентті x=f(x) (2) теңдеуімен
ауыстарайық.
ξ - (2) теңдеуінің дәл түбірі болсын.
х0 - (2) теңдеуінің қандайда бір тәсіл көмегімен алынған жуық түбірі болсын.
х0 мәнін (2) теңдеуінің оң жағына қойып
x1=f(x0) - анықтаймыз.
Енді х1 - дің мәнін (2) теңдеуінің оң жағына қойсақ, онда х2 мәні табылады.
х2=f(x1)
Осы үрдісті әрі қарай жалғастырсақ, онда х0, х1, х2, . . . , хn . . . (3) шексіз сандар тізбегін аламыз. Бұл тізбек -
итерация тізбегі деп аталады. Сонымен төмендегідей тізбекті аламыз:
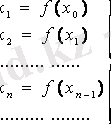 (4)
(4)
Теорема: Егер (3) тізбегі жинақты болып, f(x) функциясы үзіліссіз болса, онда (3) тізбегінің шегі (2) теңдеуінің
түбірі болады.
Шындығында да

болсын дейік.
Онда (4) - те шекке көшсек:
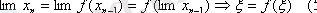 теорема дәлелденді.
теорема дәлелденді.
Итерация әдісінің көмегімен теңдеудің түбірін анықтау әр уақытта мүмкін емес. Себебі кейде итерациялық тізбек жинақты, кейде жинақсыз болуы мүмкін. Сондықтан итерация үрдісінің жинақты болуы үшін, жеткілікті шартты
анықтау қажет. Ол үшін анализ курсынан белгілі төмендегі теорема қолданылады.
Егер f(x) функциясы:
 ([a, b] аралығында өзіне - өзі бейнеленсе)
([a, b] аралығында өзіне - өзі бейнеленсе)
[a, b] дифференциалданса
 болатындай 0<q<1 табылса,
болатындай 0<q<1 табылса,
онда f(x) =0 теңдеуінің жалғыз түбірі
 болады және xn=f(xn-1) (n=1, 2, . . . )
болады және xn=f(xn-1) (n=1, 2, . . . )
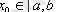 тізбегі осы түбірге жинақталады.
тізбегі осы түбірге жинақталады.
Итерация әдісінің геометриялық мағынасы:
y





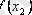
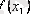
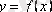

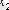


Итерациялық үрдіс әрқашанда жинақты болуы мүмкін емес. Сондықтан итерациялық үрдістің жинақты
болуының жеткілікті шартын қарастыру кажет. Ол төмендегі теоремадан анықталады.
Теорема:
 теңдеуінің
теңдеуінің
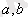 кесіндісінде жалғыз түбірі болсын және төмендегі шарттар орындалсын:
кесіндісінде жалғыз түбірі болсын және төмендегі шарттар орындалсын:
1.
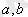 кесіндісінде
кесіндісінде
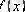 функциясы анықталған және дифференциалданады.
функциясы анықталған және дифференциалданады.
2. кез келген
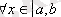 үшін
үшін
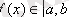 өзіне - өзі бейнеленеді.
өзіне - өзі бейнеленеді.
3.
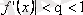 шарты орындалатын қайсыбір q нақты саны табылады,
шарты орындалатын қайсыбір q нақты саны табылады,
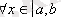 .
.
Онда кез келген бастапқы мүшесі
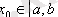 мен алынған
мен алынған
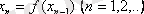 итерациялық тізбегі жинақты
итерациялық тізбегі жинақты
болады.
Дәлелдеуі: кез келген бастапқы мүшесі бар
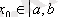
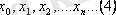 тізбегін қарастырайық. Теореманың екінші
тізбегін қарастырайық. Теореманың екінші
шарты бойынша оның барлық мүшелері

Көршілес орналасқан екі жуықтауды қарастырайық:
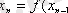 және
және
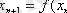
Лагранж теоремасы бойынша:
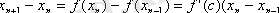 мұндағы
мұндағы
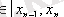
Теореманың 3 - шартын қолданып, модульге көшсек:
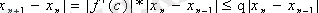 яғни:
яғни:
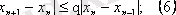
 десек, онда
десек, онда
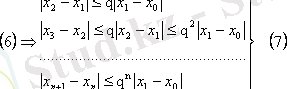
Төмендегі қатарды қарастырайық :
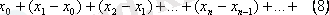
(8) қатарының дербес қосындыларын қарастырсақ:
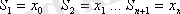 ,
,
онда
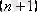 -ші дербес қосындысы (4) итерациялық тізбектің n - ші мүшесімен сәйкес келетіндігін көреміз.
-ші дербес қосындысы (4) итерациялық тізбектің n - ші мүшесімен сәйкес келетіндігін көреміз.
Яғни:
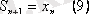
Енді (8) - ші қатарды төмендегідей қатармен салыстырайық:
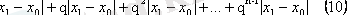
(7) қатынастарының көмегімен (8) қатарының мүшелерінің абсолюттік мәндері (10) қатарының сәйкес
мүшелерінен артық болмайды. (мұнда х0 есепке алынбайды. ) Ал (10) қатар шексіз геометриялық прогрессия
сияқты жинақталады, себебі теореманың 3 - шарты бойынша q<1. Олай болса (8) қатар жинақты, яғни оның
дербес қосындысының шегі ақырлы (9) .
Яғни
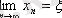 болсын. Ал
болсын. Ал
 функциясы үзіліссіз болғандықтан
функциясы үзіліссіз болғандықтан
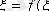 сонымен
сонымен
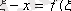 теңдеуінің
теңдеуінің
түбірі.
Теореманың шарттары қажетті болып табылмайды, яғни итерациялық тізбек бұл шарттар орындалмаған жағдайда да жинақты болуы мүмкін. Енді итерация әдісінің қатесін қарастырайық.
Жоғарыда қарастырған теоремадан, оның шарттары орындалған жағдайда, итерациялық тізбек кез келген бастапқы мүшемен жинақты болатындығын көреміз. Бұдан итерациялық үрдістің кез келген n - ші жуықтауын алғашқы жуықтау ретінде алуға болатындығы анықталады. Ал бұл жуықтап есептеу кезінде жіберілген қателер оның қортынды нәтижесіне әсерін тигізбейтіндігін көрсетеді. Сондықтан итерация әдісі теңдеулерді шешу әдістерінің ішіндегі ең жақсы, дәлдігі жоғары әдіс болып табылады. Бірақ практикада итерациялық үрдісті шексіз жүргізе беруге болмайды, оны үзуге тура келеді, яғни әдіс қателігі жіберіледі. Осы әдіс қателігінің шамасын
қарастырайық.
 - (2) теңдеуінің дәл шешімі болсын.
- (2) теңдеуінің дәл шешімі болсын.
 - (2) теңдеуінің жуықтауы ( жуық шешімі ) болсын. Сонда:
- (2) теңдеуінің жуықтауы ( жуық шешімі ) болсын. Сонда:
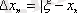 (11)
(11)
(8) бен (9) ескере отырып:
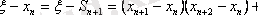 (12)
(12)
Енді (12) ні (10) қатарының қалдығымен салыстырайық:
(
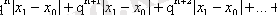 )
)
мұнда (7) бағаларын ескерсек:
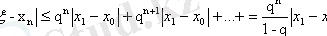
Сонымен:
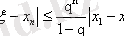 (13)
(13)
Практикада (13) формуласының орнына, оның модификациялары қолданылады.
Итерациялық үрдістің алғашқы жуықтауы ретінде
 қалауымызша алынады, яғни
қалауымызша алынады, яғни
 ретінде тізбектің кез келген
ретінде тізбектің кез келген
мүшесін алумызға болады. Мысалы:
 онда
онда
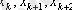 - итерациялық тізбек.
- итерациялық тізбек.
Сондықтан (13) - тегі
 ретінде
ретінде
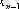 алуға болады. Ал
алуға болады. Ал
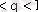 болғандықтан
болғандықтан
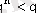
Сонымен (13) формуласының төмендегідей модификатциясын қолдануға болады:
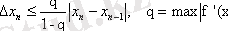 (14)
(14)
Мұндағы
 - ді
- ді
 туындысының модулінің жоғарғы шекарасы ретінде қарастыруға болады.
туындысының модулінің жоғарғы шекарасы ретінде қарастыруға болады.
Егер
 теңдеуін
теңдеуін
 дейінгі дәлдікпен итерация әдісінің көмегімен шешу қажет болса, онда итерация үрдісін
дейінгі дәлдікпен итерация әдісінің көмегімен шешу қажет болса, онда итерация үрдісін
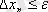 болғанша жүргіземіз, яғни:
болғанша жүргіземіз, яғни:
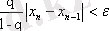 (15)
(15)
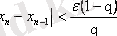
(16) теңсіздігі орындалғанша жүргіземіз.
Блок сызбасы:
Сызықты емес теңдеулер жүйесін шешудің сандық әдістері
Екі теңдеуден тұратын екі белгісізді сызықты емес теңдеулер жүйесін қарастырайық:
(2. 7)
Бұл есептің мақсаты - екі теңдеудің графигінің қиылысу нүктелерін анықтау.
Ньютон әдісі
Екі теңдеудің графигін сызып екеуінің қиылысу нүктелері жатқан облысты белгілейміз де осы облыстан жуықтап бастапқы жуықтауларды (x0, y0) таңдап аламыз ([3] қараңыз) . Келесі жуықтауларды мына формулалармен есептейміз:
Мұндағыякобиан деп аталады.
Бұл әдіс бастапқы жуықтаулар түбірге жақын алынған уақытта тиімді.
Мысалы:
жүйесі берілген. Теңдеулердің графигін сызу (2-суретте. ) арқылы бастапқы жуықтауларды табамыз
2-сурет -жәнефункцияларының графиктері
2-суреттен көріп отырғанымыздай, x0=1. 2; y0=1. 7 деп аламыз.
Якобианды есептейміз:
; n=0, 1, 2, . .
Ньютон формуласына қойсақ:
осылайша біртіндеп (х2, у2), (х3, у3), . . . жұптарының мәндерін F және G функцияларының мәні нөлге жуықтағанша есептейміз.
Қарапайым итерация әдісі
(2. 7) -ші жүйе берілсін. Бұл әдісті қолданбас бұрын жүйені итерациялық түрге келтіріп алады:
(2. 8)
Теңдеулердің графиктерін құру арқылы бастапқы жуықтауларды беріп, келесі жуықтауларды мына формуламен есептейді:
n=0, 1, 2, . . . (2. 9)
Бұл әдістің жинақтылығын теореманың шарттарымен тексеру керек.
Теорема 1. 4: Әлдебір тұйықоблыста (2. 7) -ші
жүйенің жалғыз шешімдері бар болсын:. Егер:
анықталған және үзіліссіз болса,
2 бастапқы және келесі жуықтаулардың барлығы осы облыста жатса,
3 осы облыста мына теңсіздіктер орындалса:
(2. 10)
онда (2. 8) -ші итерациялық процесс өзінің жалғызшешіміне жинақталады, яғни, .
Қателігін бағалау:
. M=max(q1; q2) .
Кей жағдайда (2. 8) -ші итерациялық процестің орнына Зейдель процесін қолдануға болады:
n=0, 1, 2, . . . (2. 11)
Итерация әдісі
Сызықты алгебралық жүйе берілсін:
(35)
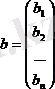
матрицаларын енгізе отырып, жүйені келесі матрицалық теңдеу түрінде жазуға болады:
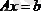 (36)
(36)
Диагональдық коэффициенттер
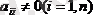 деп ұйғарып, (35) жүйесінің бірінші теңдеуін
деп ұйғарып, (35) жүйесінің бірінші теңдеуін
 -ге, екіншісін
-ге, екіншісін
 -ге, т. с. с. қатысты
-ге, т. с. с. қатысты
шешеміз. Онда мынадай келесі жүйені аламыз:
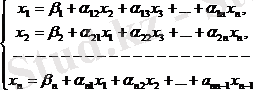 (37)
(37)
мұндағы
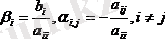 және
және
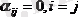
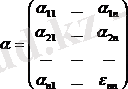
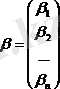
матрицаларын енгізіп, (37) жүйені
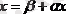 (38)
(38)
матрицалық формасы түрінде жазуға болады.
(38) жүйені шешу үшін тізбектелген жуықтау әдісін қолданамыз. Бастапқы жуық мәні үшін
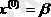 бос мүшелер бағанын аламыз.
бос мүшелер бағанын аламыз.
Одан кейін тізбектей бағана-матрицаларды құрамыз:
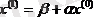 ,
,
бірінші жуықтауды
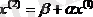 , . . . ,
, . . . ,
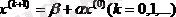 (39)
(39)
формуласы бойынша есептейміз.
Егер
 жуықтаулар тізбегінің шегі
жуықтаулар тізбегінің шегі
 болса, онда бұл шек (37) жүйенің шешімі болады.
болса, онда бұл шек (37) жүйенің шешімі болады.
Бұл жағдайда (39) теңдікте шекке көшсек келесіні аламыз:
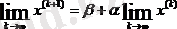
немесе
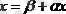
яғни шекті вектор (37) жүйенің шешімі болғандықтан, ол (35) жүйенің де шешімі болады.
Жуықтаулар формуласын кеңейген түрде жазайық:
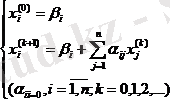 (40)
(40)
Кейбір жағдайларда (35) жүйесін коэффициенттер нөлге тең болмайтындай (37) жүйесіне келтіру тиімді екенін ескеру қажет.
Мысалы,
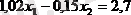 жуықтаулар тізбегі әдісін қолдану үшін келесі түрде жазылуы мүмкін:
жуықтаулар тізбегі әдісін қолдану үшін келесі түрде жазылуы мүмкін:

Дәл осы әдіспен жүйені мына түрде жазады:
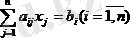 , мұндағы
, мұндағы
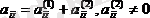 .
.
Онда берілген жүйе келтірілген жүйеге эквивалентті. Сондықтан ары қарай
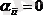 деп ұйғармайтын боламыз.
деп ұйғармайтын боламыз.
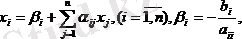
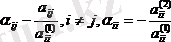
(39) немесе (40) формуламен анықталатын тізбектелген жуықтау әдісі итерация әдісі деп аталады.
Егер
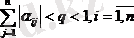 болса, онда (40) жүйе жинақы болады да, (35) жүйенің шешімін анықтауға болады.
болса, онда (40) жүйе жинақы болады да, (35) жүйенің шешімін анықтауға болады.
Басқа сөзбен айтқанда, жүйенің диагональдық коэффициенттерінің модулі диагональ емес коэффициенттерінен анағұрлым үлкен
болғанда жүйеге итерация әдісін қолдануға болады.
Мысал. Жүйені шешу керек.
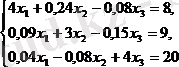 (41)
(41)
Шешуі:
Мұнда жүйенің 4, 3, 4 диагональдық коэффициентері басқа коэффициенттерден үлкен, сондықтан итерация әдісін қолдануға
болады. Осы жүйені қалыпты түрге келтірейік:
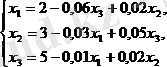 (42)
(42)
Матрицалық формада (42) жүйені былай жазуға болады: (41) жүйенің түбірінің нөлдік жуықтауы ретінде келесіні аламыз
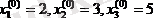
Бұл мәндерді (42) жүйенің оң жағына қойып, түбірлердің бірінші жуықтауын аламыз:
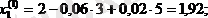
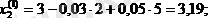
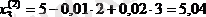
Ары қарай осы табылған жуықтауларды (42) формулаға қойып, екінші жуықтауларды аламыз:
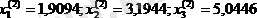
Жаңа мәндерді орнына қойып, келесі үшінші жуықтауларды аламыз:

Есептеулер нәтижесін кестеге толтырайық:
Кесте 1

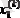
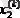
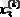
0
1
2
3
2
1, 92
1, 9094
1, 90923
3
3, 19
3, 1944
3, 19495
5
5, 04
5, 0446
5, 04485
Жүйені итерациялық түрге келтіру
(2. 7) -ші жүйені (2. 8) -ші итерациялық түрге келтіру үшін келесі тәсілдерді қолданған дұрыс.
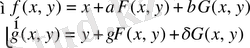 ,
,
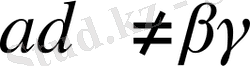 болсын. (2. 12)
болсын. (2. 12)
Коэффициенттерді мына жүйеден табамыз:
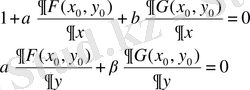
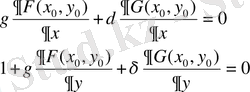 (2. 13)
(2. 13)
Параметрлерді осылай таңдап алу арқылы (2. 10) -ші шарттың орындалуын талап етуге болады.
1-мысал:
Берілген жүйе үшін итерациялық функцияларды таңдау.
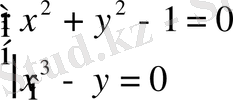
х0=0. 8, y0=0. 55
Шешімді мына түрде іздейміз:
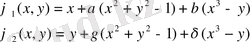 (2. 14)
(2. 14)
Коэффициенттерді анықтау үшін (2. 13) -жүйе құруымыз керек, ол үшін дербес туындылардағы мәндерді есептейміз:
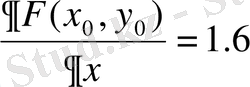
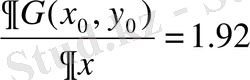
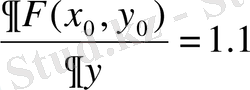 (2. 15)
(2. 15)
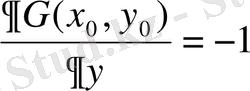 .
.
(2. 15) -ті (2. 13) -ке қойсақ:
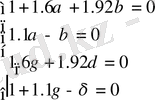 (2. 16)
(2. 16)
(2. 16) -ны шешеміз:
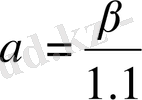 ,
,
 ,
,
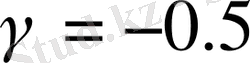 ,
,
 . Сонда
. Сонда
 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz