Модификацияланған Жордан жоюлары: теориясы мен симплекс әдісіндегі қолданылуы


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:
Профессор К. Д. Көлекеев, магистрант И. Файзиева.
Модифицирленген Жордан жоюлары.
Экономикалық сызықтық модельдер көптеген мәселелерді математикалық әдіспен шешуде қолданылады.
Сызықтық модельдерді шешуде симплекс әдісінің орны ерекше. Симплекс әдісінің бірнеше жетілдірілген түрлері белгілі. Осы әдістердің барлығы сызықтық жүйелердегі Жордан жоюларына негізделген.
1. Қарапайым Жордан жоюлары .
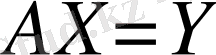 сызықтық жүйесі берілсін. Мұндағы
сызықтық жүйесі берілсін. Мұндағы
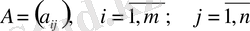

Жүйені ашып жазсақ

(1)
Бұл жүйені кесте түрінде жазу ыңғайлы
x 1 … х s … х n
a 11 … a 1s … a 1n
. .
a r1 … a rs … a r n
. .
a m1 … a ms … a mn
у 1 =
. . .
у r =
. . .
у m =
Шешуші элементі а rs ≠ 0, шешуші жолы r , шешуші бағаны s болатын кәдімгі Жордан жоюының қадамы деп y r және x s айнымалыларының орындарын ауыстыратын схемалық операцияны айтады, яғни
y r = a r1 x 1 +a r2 x 2 + … + a rs x s + … + a rn x n
теңдеуін x s бойынша шешіп, оны барлық қалған теңдеулерге қойып, жаңа кесте құруды айтады.
x 1 x 2 … y r … х n
b 11 b 12 … a 1s … b 1n
b 21 b 22 … a 2s … b 2n
. .
-a r1 -a r2 … 1 … -a rn
.
b m1 b m2 … a ms … b mn
у 1 =
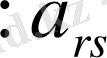 y
2
=
y
2
=
. . .
x s =
. . .
у
m
=
Мұндағы таблицаның барлық элементтері
a
rs
ке бөлінеді және
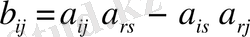
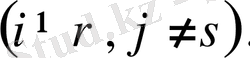
Шынында да, егер a rs ≠ 0 болса, онда

және

=

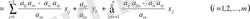
Сонымен, a rs шешуші элементімен жордан түрлендіруінің бір қадамы мынадай бес қағида бойынша (2) таблицаны жаңа (3) таблицаға келтіреді.
- шешуші элемент бір санымен алмасады;
- шешуші бағанның басқа элементтері өзгеріссіз қалады;
- шешуші жолдың басқа элементтерінің тек таңбалары ауысады;
- элементтері мына формула бойынша есептелінеді:
- жаңа таблицаның барлық элементтері шешушіarsэлементіне бөлінеді.
Мысал.
x 1 х 2 х 3
1 -2 3
-1 1 2
2 -1 -1
у 1 =
у 2 =
у 3 =
таблицасына шешуші 2-ші жол және 3 бағанмен жордан жоюын пайдалансақ, онда
x 1 х 2 у 2
5 -7 3
1 -1 1
3 -1 -1
у 1 =
х 3 =
у
3
=
және
x 1 х 2 у 2

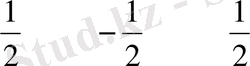
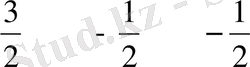
у 1 =
х 3 =
у 3 =
2. Стейниц теоремасы.
Егер (1) жүйенің барлық сызықты формалары сызықты тәуелсіз (яғни, m ≤ n) болса, онда m сәйкес жордан түрлендірулерін пайдалана отырып барлық m тәуелді, y 1 , …, y m айнымалыларын m тәуелсіз айнымалыларына келтіру мүмкін.
3. Модифицирленген Жордан жоюлары .
Анықтама. Жордан жоюларының кейбір қолдануларында, мысалы симплекс әдісінде, шешуші жолдың элементтері таңбаларын сақтауы, ал шешуші бағанның элементтерінің таңбалары қарама-қарсы таңбаға ауысулары қажет. Мұндай жағдайларда кәдімгі жордан жоюларының орнына (1) жүйені келесідей жазатын
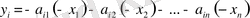 (1')
(1')
( i=1, …, m )
таблицасы
- x 1 -x 2 … -х s … -х n
a 11 a 12 … a 1s … a 1n
. .
a r1 a r2 … a rs … a r n
. .
a m1 a m2 … a ms … a mn
у 1 =
. . .
у r =
. . .
у m =
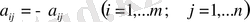
болатын модифицирленген жордан жоюлары қолданылады.
a rs шешуші элементті модифицирленген жордан жоюын пайдаланып мынадай жаңа таблицаға ие боламыз:
- x 1 -x 2 … -y r … -х n
b 11 b 12 … -a 1s … b 1n
. .
a r1 a r2 … 1 … a rn
.
b m1 b m2 … -a ms … b mn
у 1 =
. . .
x s =
. . .
у m =
мұнда
2) шешуші жолдың басқа элементтері өзгеріссіз қалады;
3) шешуші бағанның басқа элементтерінің таңбалары ауысады.
Шынында да,
y r = a r1 (-x 1 ) + a r2 (-x 2 ) + … + a rs (-x s ) + … + a rn (-x n )
теңдеуінен мынаны аламыз:
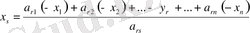
Мысал.
Бізге мынадай жүйе берілген:
y 1 = 2x 1 - x 2 + 3x 3 ,
y 2 = -x 1 +4x 2 -2x 3 ,
y 3 = 5x 1 +2x 2 -4x 3
Бұл жүйені келесідей таблица түрінде өрнектейміз
- x 1 -х 2 -х 3
-2 1 -3
1 -4 2
-5 -2 4
у 1 =
у 2 =
у 3 =
және шешуші 2-ші қатар, 3-і бағанмен жордан жоюын пайдалансақ, онда мынадай нәтижеге ие боламыз:
- x 1 -х 2 -у 2
-
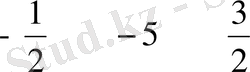


у 1 =
х 3 =
у 3 =
Пайдаланылған әдебиеттер:
- Ашманов С. А. Линейное программирование. -М. : Наука, 1981. 304 б.
- Карманов В. Г. Математическое программирование. М. 1986. 288 б.
- Зуховицкий С. И., Авдеева Л. И. Линейное и выпуклое программирование. М. 1967.
- Құлекеев Ж. Ә. Сызықтық программалау негіздері. Алматы. 1991. 156 б.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz
