Температураға тәуелді материал қасиеттері бар көпқабатты цилиндрдің термосерпімділік кернеулік күйін сандық есептеу және талдауы


А. Ясауи университетініњ хабаршысы, №1, 2011
М. Ж. ЖҰМАБАЕВ
физика-математика ғылымдарының докторы, профессор
Д. А. ХИЛЬВЕТОВА
А. Ясауи атындағы ХҚТУ-нің магистранты
ТЕРМОСЕРПІМДІЛІК ЕСЕБІ
В статье рассматривается решение задачи о напряженном состоянии многослойного цилиндра, помещенного в температурном поле. Приводится анализ полученных численных результатов.
The article considers the problem of the stress state of multilayered cylinders placed in a temperature field. The analysis of the obtained numerical results is given.
Техникада көптеген цилиндр формалы құрылғылар эксплуатация кезінде сыртқы күштер мен температура өрісінде жұмыс істейді. Шындығында, құрылғы материалдарының қасиеттерін сипаттайтын функциялар температураға тәуелді болады. Алынған дифференциалдық теңдеулердің аналитикалық шешімін алу мақсатында бұл тәуелділікті апроксимациялайды. Материал қасиеттерінің температураға тәуелділігін апроксимациялау алынған есеп шешімінің қолдану аясын тарылтады. Сондықтан құрылғы материалдарының қасиеттерін сипаттайтын функциялардың температураға тәуелділігін эксперимент арқылы алынған кесте немесе қисық түрінде пайдалану тиімді [1-6] .
Осесимметриялық температуралық өрісте орналасқан, көп қабатты цилиндрдің кернеулік күй есебі қарастырылады. Оның ішкі радиусы
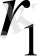 , ал сыртқы радиусы
, ал сыртқы радиусы
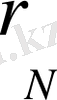 болсын
болсын
 (
(
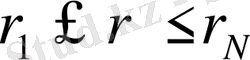 ) . Цилиндр осесимметриялық температуралық өрісте (
) . Цилиндр осесимметриялық температуралық өрісте (
 ) орналасқан. Қабаттар материалдарының қасиеттері әртүрлі функциялармен сипатталады, яғни
) орналасқан. Қабаттар материалдарының қасиеттері әртүрлі функциялармен сипатталады, яғни
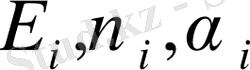 - і-ші қабаттың қасиеттерін анықтайды (
- і-ші қабаттың қасиеттерін анықтайды (
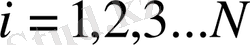 ) .
) .
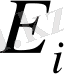 - серпімділік модулі,
- серпімділік модулі,
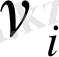 - Пуассон коэффициенті,
- Пуассон коэффициенті,
 - сызықтықтың ұлғаю коэффициенті. Бұл коэффициенттер температураға тәуелді, яғни
- сызықтықтың ұлғаю коэффициенті. Бұл коэффициенттер температураға тәуелді, яғни
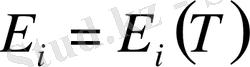 ,
,
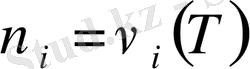 ,
,
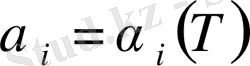 (1)
(1)
эксперимент арқылы анықталынады.
Цилиндрдегі қабаттар арасында
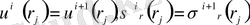 (2)
(2)
шарттары орын алады. Мұнда
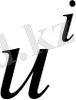 ,
,
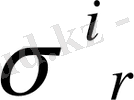 - радиальдық орын ауыстыру мен кернеу функциялары,
- радиальдық орын ауыстыру мен кернеу функциялары,
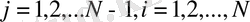 ,
,
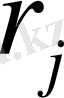 ,
і
- мен
(і+1) -
қабаттар арасындағы радиус.
,
і
- мен
(і+1) -
қабаттар арасындағы радиус.
Жанасу беттерінде температура үшін
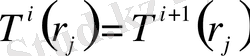
шарттары орын алады.
Цилиндрдің кернеулік күйі есебін шешу
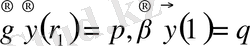 (3)
(3)
шарттарын қанағаттандыратын,
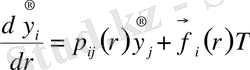 (4)
(4)

түріндегі кесек-үзікті айнымалы коэффициентті дифференциалдық теңдеулерді шешуге алып келеді. Мұнда
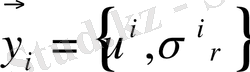 - ізделінді функция,
- ізделінді функция,
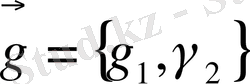 ,
,
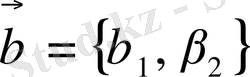 векторларының компоненттері 0 немесе 1-ді қабылдайды,
p
мен
q
- есептің шартына байланысты берілетін белгілі шамалар
векторларының компоненттері 0 немесе 1-ді қабылдайды,
p
мен
q
- есептің шартына байланысты берілетін белгілі шамалар
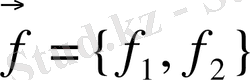 . (4) теңдеудегі
. (4) теңдеудегі
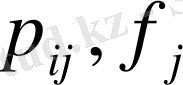
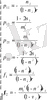
 (5)
(5)
теңдіктерімен анықталынады,
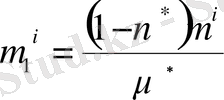 .
.
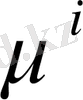 - жылжу коэффициенті,
- жылжу коэффициенті,
 - Пуассон коэффициенттерінің орташа мәні.
- Пуассон коэффициенттерінің орташа мәні.
Кернеу компоненттері
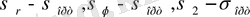 және деформация компоненттері арасындағы байланыс
және деформация компоненттері арасындағы байланыс
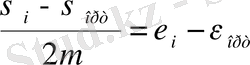 (6)
(6)
түрінде алынады. Мұнда
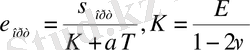
Цилиндрдің термосерпімділік есебін шешу, (2), (3) шарттарды қанағаттандыратын, (4) дифференциалдық теңдеулер жүйесін шешуге, яғни шеттік есепке алып келеді.
(4) теңдеулер жүйесінің шешімінің әрбір қабаты үшін Коши есебінің екі сызықтық-тәуелсіз суперпозициясының шешімі сандық түрде табылады. Ол үшін
 қалыңдығының
қалыңдығының
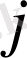 -ші қабаты
-ші қабаты
 - тең кесіндісіне бөлінеді. Әр кесіндісіндегі температураның таралуы сызықтық деп есептелінеді және кесіндінің соңдарында оның берілген мәндерімен апроксимацияланады. Берілген созылу диаграммасын
- тең кесіндісіне бөлінеді. Әр кесіндісіндегі температураның таралуы сызықтық деп есептелінеді және кесіндінің соңдарында оның берілген мәндерімен апроксимацияланады. Берілген созылу диаграммасын
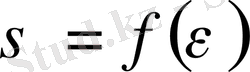 қолдана отырып, қарастырылып отырған,
қолдана отырып, қарастырылып отырған,
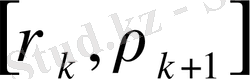 кесіндісіндегі нүктеде температура анықталынады және температура мәні үшін
кесіндісіндегі нүктеде температура анықталынады және температура мәні үшін
 ~
~
 қисығы құрылады
қисығы құрылады
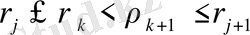 . Сосын
. Сосын
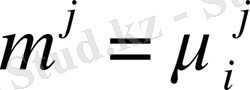 ағымдағы мәні, ал
ағымдағы мәні, ал
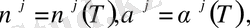 қисықтарынан
қисықтарынан
 ,
,
 параметрлер ағымдағы мәні табылады. Мұнда
параметрлер ағымдағы мәні табылады. Мұнда
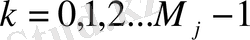
Табылған
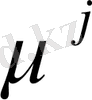

 мәндері берілген температура деңгейіне сәйкес
мәндері берілген температура деңгейіне сәйкес
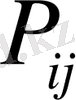 - компоненттерін
- компоненттерін
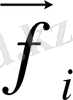 векторларын толығымен анықтауға мүмкіндік береді.
векторларын толығымен анықтауға мүмкіндік береді.
Әрбір ішкі бетте, екі сызықтық тәуелсіз шарттар үшін Рунге-Кутта әдісімен [7] және
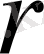 радиусы бойынша
радиусы бойынша
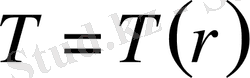 температурасы ескеріліп айнымалы коэффициентті сызықтық дифференциалдық (4) теңдеулер жүйесінің
температурасы ескеріліп айнымалы коэффициентті сызықтық дифференциалдық (4) теңдеулер жүйесінің
 -ші қабат үшін екі
-ші қабат үшін екі
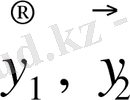 сызықтық тәуелсіз шешімі алынады. Сызықтық интегралдар комбинациясы әдісі негізінде қабаттар үшін
сызықтық тәуелсіз шешімі алынады. Сызықтық интегралдар комбинациясы әдісі негізінде қабаттар үшін
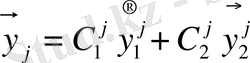 түрінде жалпы шешімі алынады. Мұндағы
түрінде жалпы шешімі алынады. Мұндағы
 - тұрақтылар
- тұрақтылар
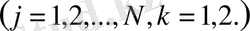 Бұл тұрақтылар саны 2
Бұл тұрақтылар саны 2
 -ге тең. Қабаттар арасындағы (2) шартты пайдалансақ, онда
-ге тең. Қабаттар арасындағы (2) шартты пайдалансақ, онда
 тұрақтысына қатысты 2
тұрақтысына қатысты 2
 -2 алгебралық теңдеу, ішкі
-2 алгебралық теңдеу, ішкі
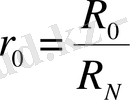 және сыртқы
және сыртқы
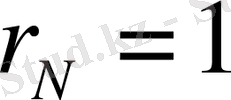 бетінде (3) шарт
бетінде (3) шарт
 тұрақтысына қатысты тағы екі теңдеу алуға көмектеседі. Нәтижесінде,
тұрақтысына қатысты тағы екі теңдеу алуға көмектеседі. Нәтижесінде,
 тұрақтысына қатысты тұрақтыны анықтау үшін 2
тұрақтысына қатысты тұрақтыны анықтау үшін 2
 алгебралық теңдеуінен тұратын тұйық сызықтық жүйе алынады:
алгебралық теңдеуінен тұратын тұйық сызықтық жүйе алынады:
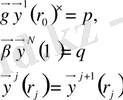
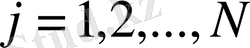
Бұл жүйені Гаусс әдісімен шешсек, онда
 тұрақтылары анықталынады. Интегралдардың сызықтық комбинация әдісін
тұрақтылары анықталынады. Интегралдардың сызықтық комбинация әдісін
 -ші қабат үшін қолдану ізделінді шешімді құруға көмектеседі.
-ші қабат үшін қолдану ізделінді шешімді құруға көмектеседі.
 -ші қабатты кернеулік - деформацияланған күйі
-ші қабатты кернеулік - деформацияланған күйі
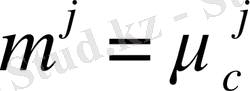 жағдайына сәйкес келеді.
жағдайына сәйкес келеді.
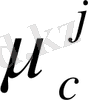 қозғалысының айнымалы мәні
қозғалысының айнымалы мәні
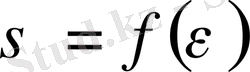 қисығы көмегімен табылады. Алынған кернеулік және деформациялық компоненттер бойынша
қисығы көмегімен табылады. Алынған кернеулік және деформациялық компоненттер бойынша
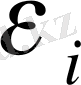 деформациясы мен
деформациясы мен
 кернеулігінің интенсивтілігі есептелінеді.
кернеулігінің интенсивтілігі есептелінеді.
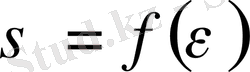 қисықтан
қисықтан
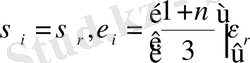 қатынастарын қолдана отырып,
қатынастарын қолдана отырып,
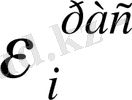 есеп-қисабына сәйкес келетін
есеп-қисабына сәйкес келетін
 табылады. Табылған
табылады. Табылған
 мәні
мәні
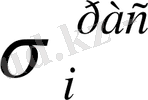 есеп-қисап мәнімен салыстырылады. Егер бұл мәндер берілген дәлдікпен өзара сәйкес келсе, онда серпімділік айнымалы параметр әдісіне сәйкес есеп шешімі аяқталды деп есептелінеді. Егер бұл сандар сәйкес келмесе, онда
есеп-қисап мәнімен салыстырылады. Егер бұл мәндер берілген дәлдікпен өзара сәйкес келсе, онда серпімділік айнымалы параметр әдісіне сәйкес есеп шешімі аяқталды деп есептелінеді. Егер бұл сандар сәйкес келмесе, онда
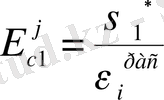 параметр мәні табылады, есеп қайта жаңа
параметр мәні табылады, есеп қайта жаңа
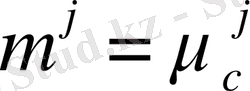 жылжу модулімен шешіледі. Сонымен қатар, параметр де созылу диаграммасы да ағымдағы температура мәнімен сәйкес келеді. Жоғарыда көрсетілген есеп қисап әдісімен
жылжу модулімен шешіледі. Сонымен қатар, параметр де созылу диаграммасы да ағымдағы температура мәнімен сәйкес келеді. Жоғарыда көрсетілген есеп қисап әдісімен
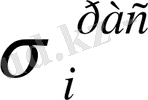 есеп-қисабы мен
есеп-қисабы мен
 жүктеме мәніне сәйкестенге дейін, есеп қайталанып шешіледі. Алынған алгоритм негізінде сандық нәтижелер алынған. Қойылған есептің сандық нәтижесін алудың блок-схемасы суретте көрсетілген.
жүктеме мәніне сәйкестенге дейін, есеп қайталанып шешіледі. Алынған алгоритм негізінде сандық нәтижелер алынған. Қойылған есептің сандық нәтижесін алудың блок-схемасы суретте көрсетілген.
Жүргізілген зерттеулер температуралық кернеу компоненттер деңгейі температура градиентіне тәуелді екенін көрсетеді. Сонымен қатар егер қарастырылған барабанның сыртқы беті ішкі бетінен қарағанда көбірек жылытылған болса, онда қысушы сақиналық
 және
және
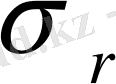 радиальдық кернеу компоненттері пайда болады. Көпқабаттан тұратын температуралық өрісте орналасқан барабанның кернеулік күйі зерттелді. Ішкі қабатты титан қорытпасынан, ал одан кейін боралюминийден тұратын қабаттармен алмасып орналасқан. Қабаттардың әртүрлі қалыңдықтары үшін сандық нәтижелер алынды. Неғұрлым сызықтық ұлғаю коэффициенттері үлкен барабандарда
радиальдық кернеу компоненттері пайда болады. Көпқабаттан тұратын температуралық өрісте орналасқан барабанның кернеулік күйі зерттелді. Ішкі қабатты титан қорытпасынан, ал одан кейін боралюминийден тұратын қабаттармен алмасып орналасқан. Қабаттардың әртүрлі қалыңдықтары үшін сандық нәтижелер алынды. Неғұрлым сызықтық ұлғаю коэффициенттері үлкен барабандарда
 ,
,
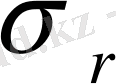 кернеу компоненттерінің мәні де ұлғаяды. Мұның әсері, әсіресе
кернеу компоненттерінің мәні де ұлғаяды. Мұның әсері, әсіресе
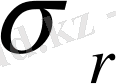 кернеу компонентінде айтарлықтай. Зерттеу нәтижесінде, қалыңдатылған барабанда ең кіші мәнін көруге болады.
кернеу компонентінде айтарлықтай. Зерттеу нәтижесінде, қалыңдатылған барабанда ең кіші мәнін көруге болады.
↓
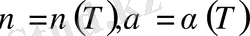 енгізіледі, әрі әртүрлі температура деңгейі үшін созылу диаграммасы енгізіледі
енгізіледі, әрі әртүрлі температура деңгейі үшін созылу диаграммасы енгізіледі
↓
Ағымдағы қабаттың нүктелік бөлшектену
бойынша цикл басы
↓
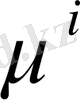 есептелінеді, температура үлестірілуі мен
есептелінеді, температура үлестірілуі мен
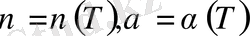 ,
,
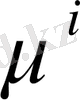
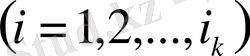 анықталады
анықталады
↓
↓
1-сурет. Блок - сызба
↓
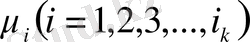
↓
↓
↓
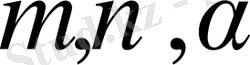 табылады
табылады
↓
↓
↓
↓
↓
 тұрақтыны интегралдауға қатысты алгебралық теңдеулер жүйесі
тұрақтыны интегралдауға қатысты алгебралық теңдеулер жүйесі
↓
2-сурет. Блок - сызба
↓
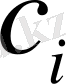 бойынша
бойынша
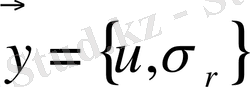 есептелінеді
есептелінеді
↓
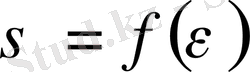 ескеріледі
ескеріледі
↓
↓
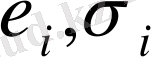 есептелінуі
есептелінуі
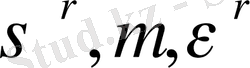
↓
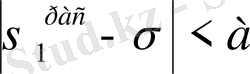
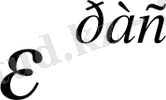 үшін созылу диаграммасынан
үшін созылу диаграммасынан
 табылады
табылады
жоқ иә

↓
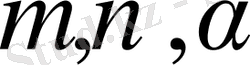 мен деформация компоненті мен күштік компоненттер жазылады
мен деформация компоненті мен күштік компоненттер жазылады
↓
↓
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz