Фредгольм мен Вольтерра теңдеулері, интегро-дифференциалдық есептер және функционалдық анализ негіздері


Лекция 1
Негізгі ұғымдар мен интегралдық теңдеулерге
келтірілетін есептер.
І. Интегралдық кластарды кластарға бөлу.
Белгісіз функциялар интегралдардың астында кездесетін теңдеулер интегралдық теңдеулер деп аталады. егер белгісіз функция интегралдық теңдеуге сызықтық түрде қатынасса, онда теңдеуді сызықтық деп атайды.
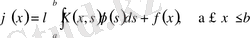 (1)
(1)
түріндегі теңдеу Фредгольмнің 2-текті сызықтық интегралдық теңдеуі деп аталады. мұндағы
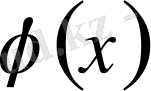 - нақты айнымалы
х
аргументіне тәуелді белгісіз функция,
- нақты айнымалы
х
аргументіне тәуелді белгісіз функция,
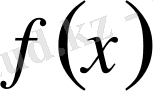 функциясы
функциясы
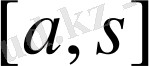 кесіндісінде,
кесіндісінде,
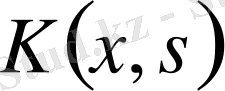 функциясы
функциясы
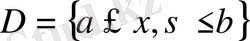 жиынында анықталған белгілі функция:
жиынында анықталған белгілі функция:
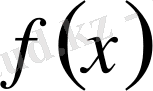 пен
пен
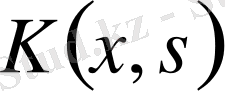 сәйкес интегралдық теңдеу бос нүктесі мен ядросы деп аталады, ал
сәйкес интегралдық теңдеу бос нүктесі мен ядросы деп аталады, ал
 - параметр. Интегралдық жоғарғы және төменгі шектері (
a
мен
b
) жалпы жағдайда тұрақты шамалар; олар шектелген де шектелмеген де болуы мүмкін. Егер
- параметр. Интегралдық жоғарғы және төменгі шектері (
a
мен
b
) жалпы жағдайда тұрақты шамалар; олар шектелген де шектелмеген де болуы мүмкін. Егер
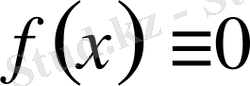 болса, онда жоғарыдағы (1) интегралдық теңдеу біртекті, ал
болса, онда жоғарыдағы (1) интегралдық теңдеу біртекті, ал
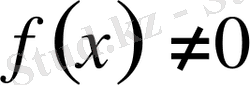 болған жағдайда - біртекті емес деп аталады.
болған жағдайда - біртекті емес деп аталады.
Фредгольмнің 1-текті интегралдық теңдеуінде белгісіз функция интегралдық мүшеде ғана қатынасады, дәлірек айтқанда, ол теңдеу
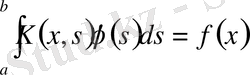
түрінде жазылады.
Вольтерраның 2-текті интегралдық теңдеуі деп
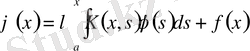 (2)
(2)
түріндегі, ал 1-текті интегралдық теңдеуі деп
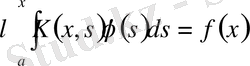
түріндегі теңдеуді айтады.
Мәселен, Фредгольмнің 2-текті интегралдық
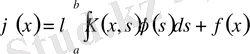 теңдеуінде ядро
теңдеуінде ядро
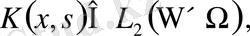 бос мүше
бос мүше
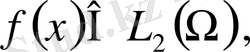 ал
ал
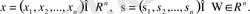 Фредгольмнің 2-текті сызықты интегралдық теңдеулері системасы
Фредгольмнің 2-текті сызықты интегралдық теңдеулері системасы
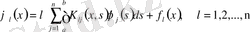
түрінде өрнектеледі. Егер
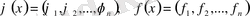 - векторлар, ал ядро
- векторлар, ал ядро
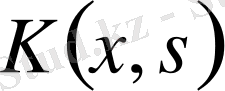 элементтері
элементтері
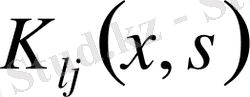 болатын матрица деп қарасақ, онда системаны (1) теңдеуі түрінде жазуға болады.
болатын матрица деп қарасақ, онда системаны (1) теңдеуі түрінде жазуға болады.
Дәл осындай екі аргументті функция үшін Вольтерра теңдеуі
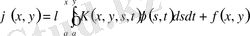
түрінде, ал системасын
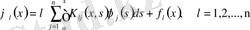
түрінде өрнектеуге болады.
Математикалық, физикалық кейбір қолданбалы есепті үшін сызықтық емес интегралдық теңдеулерді шешуге алып келеді. Сондықтан, кейбір практикалық және теориялық маңызы бар бірнеше сызықтық емес интегралдық теңдеулерді зерттеусіз келтірейік.
- Гаммерштейн теңдеуі
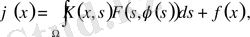
мұндағы
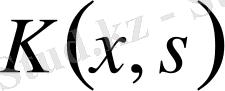 - фредгольмдік ядро.
- фредгольмдік ядро.
2) Урысон теңдеуі
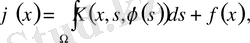
мұндағы
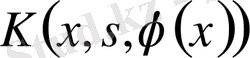 - үзіліссіз функция;
- үзіліссіз функция;
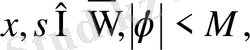 ал М - шенелген оң шама.
ал М - шенелген оң шама.
- Вольтерраның сызықты емес теңдеуі
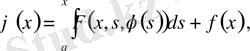
мұндағы
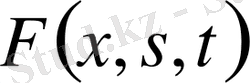 - үзіліссіз функция,
- үзіліссіз функция,
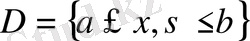 ,
,
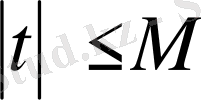 облысында анықталған.
облысында анықталған.
- Липунов-Лихтенштейн теңдеуі
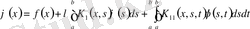
мұндағы
 мен
мен
 үзіліссіз функциялар.
үзіліссіз функциялар.
Егер теңдеулерде белгісіз функцияның интегралымен қоса туындылары да бар болса, ондай теңдеулерді интегро-дифференциалдық теңдеулер дейміз. Мысал, үшін мына ең қарапайым интегро-дифференциалдық теңдеулерді келтірейік:
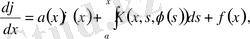 (4)
(4)
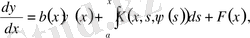 (5)
(5)
мұнда белгісіз функциялардың бірінші ретті туындылары бар болғандықтан, бұл теңдеулердің шешімі жалғыз болуы үшін қосымша
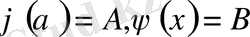 шарттары берілуі қажет.
шарттары берілуі қажет.
Қолданбалы математикада интегро-дифференциалдық сызықтық, сызықтық емес теңдеулер немесе теңдеулер системасы және жоғарғы ретті туындылы (кәдуілгі және дербес туындылы) интегро-дифференциалдық теңдеулер көп кездеседі. Мысалы
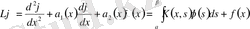
теңдеуінің
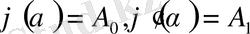 бастапқы шарттарын немесе
бастапқы шарттарын немесе
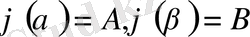 шекаралық шарттарын қанағаттандыратын шешімін табу есебін қарастыруға болады. Егер белгісіз функция көп аргументті болса, онда интегро-дифференциалдық теңдеулерде белгісіз функциялардың дербес туындылары мен интегралдары көп өлшемді болады. Интеграл астындағы өрнекте белгісіз функциялардың туындылары болатын интегро-дифференциалдық теңдеулер де жиі кездеседі. Кейбір жағдайларды интеграл астындағы туындының реті жоғары болса, онда теңдеулердің шешімдері барлық уақытта бола бермейді және шешімнің бар екенін дәлелдеген күнде оны табу оңай емес. Ал егер интеграл сыртындағы өрнекте белгісіз функциялардың туындылары жоғарғы ретті болса, көп жағдайда мұндай интегро-дифференциалдық теңдеулерді системаларға дифференциалды және интегралдық теңдеулердің системалардың жалпы теориясын пайдаланып шешуге болады.
шекаралық шарттарын қанағаттандыратын шешімін табу есебін қарастыруға болады. Егер белгісіз функция көп аргументті болса, онда интегро-дифференциалдық теңдеулерде белгісіз функциялардың дербес туындылары мен интегралдары көп өлшемді болады. Интеграл астындағы өрнекте белгісіз функциялардың туындылары болатын интегро-дифференциалдық теңдеулер де жиі кездеседі. Кейбір жағдайларды интеграл астындағы туындының реті жоғары болса, онда теңдеулердің шешімдері барлық уақытта бола бермейді және шешімнің бар екенін дәлелдеген күнде оны табу оңай емес. Ал егер интеграл сыртындағы өрнекте белгісіз функциялардың туындылары жоғарғы ретті болса, көп жағдайда мұндай интегро-дифференциалдық теңдеулерді системаларға дифференциалды және интегралдық теңдеулердің системалардың жалпы теориясын пайдаланып шешуге болады.
3-мысал ретінде (4) мен (5) теңдеулерін сызықтық интегралдық теңдеулерге келтірейік. Ол үшін
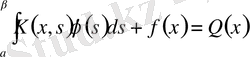
деп белгілесек, онда (4) теңдеуінен
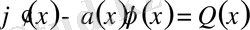 І-ретті сызықтық дифференциалдық теңдеуін аламыз. Оның шешімі
І-ретті сызықтық дифференциалдық теңдеуін аламыз. Оның шешімі
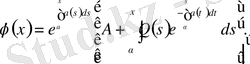
Бұл өрнекке
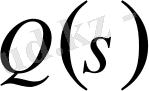 -тің мәнін қойсақ,
-тің мәнін қойсақ,
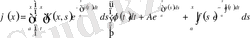
мұнда
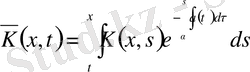 ,
,
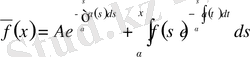
белгілеулер енгізсек, онда біз Вольтерраның 2-текті сызықтық
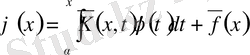
теңдеуін аламыз. Осы әдіспен (5) теңдеуін Фредгольмнің 2-текті сызықтық интегралдық теңдеуіне келтіруге болады.
2. Интегралдық теңдеуге келтірілетін есептер.
1. Абель есебі.
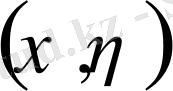 вертикаль жазықтығында материалдық нүкте өзінің ауырлық күші әсерінен қисық сызық бойымен қозғалады. Берілген
вертикаль жазықтығында материалдық нүкте өзінің ауырлық күші әсерінен қисық сызық бойымен қозғалады. Берілген
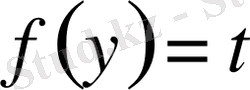 уақытта дене алғашқы жылдамдықсыз ординатасы
у
болған нүктеден
уақытта дене алғашқы жылдамдықсыз ординатасы
у
болған нүктеден
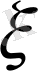 өсіне жететін қисық сызықты табу керек. Қозғалатын нүктенің жылдамдығының абсолютті шамасы:
өсіне жететін қисық сызықты табу керек. Қозғалатын нүктенің жылдамдығының абсолютті шамасы:
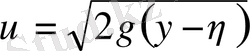 . Егер
. Егер
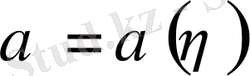 арқылы белгісіз қисықтың
арқылы белгісіз қисықтың
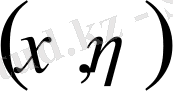 нүктесіне жүргізілген жанаманың
нүктесіне жүргізілген жанаманың
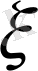 өсімен жасайтын бұрышын белгілесек, онда
өсімен жасайтын бұрышын белгілесек, онда
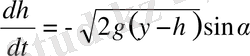
шамасы жылдамдықтың
 өсі бойынша құраушысы болады. Соңғы теңдіктен
өсі бойынша құраушысы болады. Соңғы теңдіктен
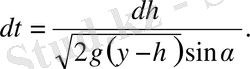
Мұны 0-ден
у-
ке дейін интегралдап
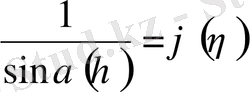 деп белгілесек, Абель теңдеуін аламыз:
деп белгілесек, Абель теңдеуін аламыз:
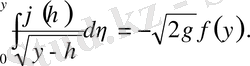
Егер бұл өрнектен
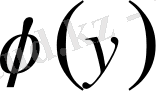 функциясын анықтасақ, онда іздеген қисық сызықты табу қиын емес.
функциясын анықтасақ, онда іздеген қисық сызықты табу қиын емес.
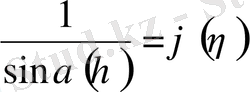 теңдігінен
теңдігінен
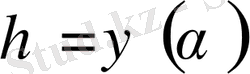 екенін анықтаймыз. Содан кейін
екенін анықтаймыз. Содан кейін
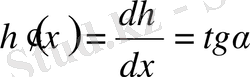 болғандықтан,
болғандықтан,
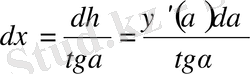 . Бұл өрнекті интегралдап
. Бұл өрнекті интегралдап
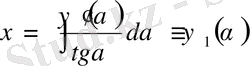
екенін анықтаймыз. Сонымен, анықтайтын сызық
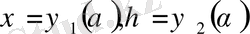 параметрлік теңдеулермен беріледі екен.
параметрлік теңдеулермен беріледі екен.
2. Шектің тербелуі.
Ұзындығы
l
серпімді шек тыныштық кезінде
ОХ
өсіндегі ОА кесіндімен дәл келсін. Шектің шекаралары О мен А нүктелерде бекітілген. Т шектің керілу күші. Шекке
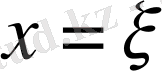 болатындай В нүктесінде вертикаль Р күші әсер етсін. Бұл күштің әсерінен ОА шек ОВ
1
А сынық сызығы түрін қабылдайды. Сонда
болатындай В нүктесінде вертикаль Р күші әсер етсін. Бұл күштің әсерінен ОА шек ОВ
1
А сынық сызығы түрін қабылдайды. Сонда
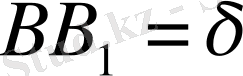 шамасын ОВ-мен және ВА-мен салыстырғанда өте аз шама деп қарастырамыз. Тепе-теңдік заңының шарты бойынша шығатыны:
шамасын ОВ-мен және ВА-мен салыстырғанда өте аз шама деп қарастырамыз. Тепе-теңдік заңының шарты бойынша шығатыны:
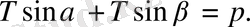
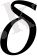 -ның өте аз шама екенін ескерсек,
-ның өте аз шама екенін ескерсек,
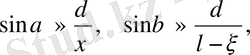
олай болса алдыңғы шарт
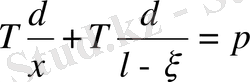
түрінде жазылады. Бұл соңғы өрнектен:
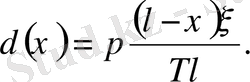
Абсциссасы
х
-ке тең С нүктесіндегі шектің иілуін
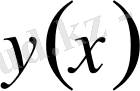 арқылы белгілейік.
арқылы белгілейік.
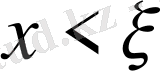 болсын.
болсын.
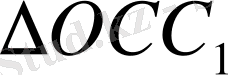 және
және
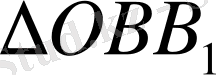 ұқсастығынан
ұқсастығынан
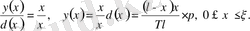
Сонымен
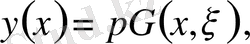 мұнда
мұнда
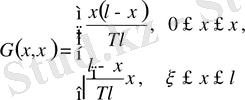
Грин формуласы деп аталады. Бұл өрнектен
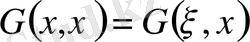 екенін оңай көруге болады. Егер шектің барлық нүктелеріне сызықтық тығыздығы
екенін оңай көруге болады. Егер шектің барлық нүктелеріне сызықтық тығыздығы
 үзіліссіз таралған күш әсер етсе, онда шектің иілуі былай:
үзіліссіз таралған күш әсер етсе, онда шектің иілуі былай:
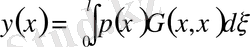 (6)
(6)
анықталады.
Мына есептерді қарастырайық.
а)
Шектің иілуі
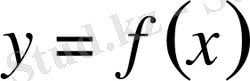 иболғанда оған әсер етуші күштің
иболғанда оған әсер етуші күштің
 тығыздығын табу керек болсын. Сонда Фредгольмнің 1-текті
тығыздығын табу керек болсын. Сонда Фредгольмнің 1-текті
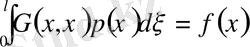
теңдеуін шешуге келеміз, яғни бұл теңдеуден белгісіз
 -ді тапсақ есеп шешілген болады.
-ді тапсақ есеп шешілген болады.
б)
Шекке уақыт өткен сайын өзгеріп тұратын абсциссасы
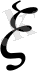 болатын нүктеде тығыздығы
болатын нүктеде тығыздығы
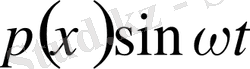 болатын күш әсер етсін. Бұл күштің әсерінен шек қозғалысқа түседі. Ол
болатын күш әсер етсін. Бұл күштің әсерінен шек қозғалысқа түседі. Ол
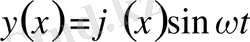 периодты тербеліспен қозғалсын. Ол кезде уақыттың
t
мезетте шектің
периодты тербеліспен қозғалсын. Ол кезде уақыттың
t
мезетте шектің
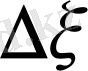 бөлігіне жоғарыдағы күштен басқа
бөлігіне жоғарыдағы күштен басқа
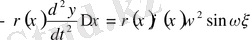 инерция күші әсер етеді. Сондықтан (6) теңдік:
инерция күші әсер етеді. Сондықтан (6) теңдік:

түрінде жазылады. Міне бұл өрнектен:
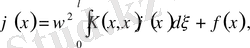
яғни
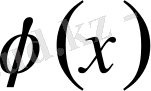 -ке қатысты Фредгольмнің 2-текті интегралдық теңдеуі алынды, мұнда
-ке қатысты Фредгольмнің 2-текті интегралдық теңдеуі алынды, мұнда
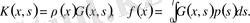
3. Дифференциалдық теңдеулер үшін Коши есебі мен шекаралық есептерді шешуді интегралдық теңдеуге келтіру. Бұл жерде біз дифференциалдық және интегралдық теңдеулер арасындағы байланысты көрсетеміз.
1)
Кәдуілгі дифференциалдық теңдеу үшін Коши есебін шешу. Вольтерраның интегралдық теңдеуіне келтіріледі. 1-ретті кәдуілгі дифференциалдық теңдеу
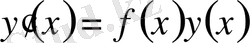 үшін бастапқы шарт
үшін бастапқы шарт
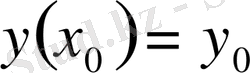 берілсін.
берілсін.
 функциясы осы Коши есебінің шешімі делік. Осы теңдеуге қойып, алынған тепе-теңдікті
функциясы осы Коши есебінің шешімі делік. Осы теңдеуге қойып, алынған тепе-теңдікті
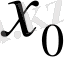 -ден
х
-ке дейін интегралдап:
-ден
х
-ке дейін интегралдап:
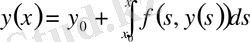
интегралдық теңдеуін аламыз. Мұның шешімі
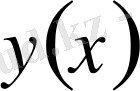 функциясы берілген есептің де шешімі екенін тексеру қиын емес.
функциясы берілген есептің де шешімі екенін тексеру қиын емес.
Коэффициенттері үзіліссіз функциялар болатын
п-
ретті сызықтық дифференциалдық теңдеу үшін Коши есебін шешу де 2-текті Вольтерраның интегралдық теңдеуін шешуге келтіріледі. Бұл жағдайда мына 2-ретті теңдеу үшін қарастырамыз:
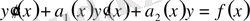 теңдеуі үшін
теңдеуі үшін
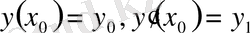 бастапқы шарттары берілсін. Бұл есепте
бастапқы шарттары берілсін. Бұл есепте
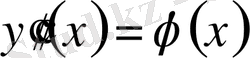 деп белгілеп, одан кейін теңдікті бастапқы шарттарды пайдаланып интегралдау нәтижесінде
деп белгілеп, одан кейін теңдікті бастапқы шарттарды пайдаланып интегралдау нәтижесінде
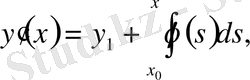
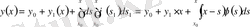
теңдеуін аламыз. Ал соңғы өрнектерді пайдаланып берілген теңдеуден
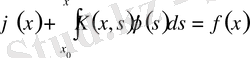
Вольтерраның 2-текті интегралдық теңдеуін аламыз, мұндағы
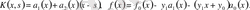
Мысалы,
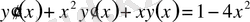 дифференциалдық теңдеуінің
дифференциалдық теңдеуінің
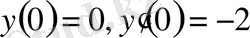 бастапқы шарттарын қанағаттандыратын шешімін табу керек.
бастапқы шарттарын қанағаттандыратын шешімін табу керек.
Осы Коши есебін интегралдық теңдеумен алмастырайық. Ол үшін белгісіз
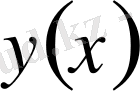 функциясының 2-ретті туындысын жаңа белгісіз
функциясының 2-ретті туындысын жаңа белгісіз
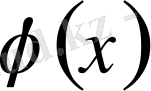 арқылы
арқылы
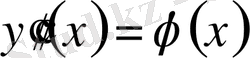 деп белгілесек, одан кейін бұл өрнектің екі жағын да 0-ден ч-ке дейін интегралдап және бастапқы шарттарды ескеріп,
деп белгілесек, одан кейін бұл өрнектің екі жағын да 0-ден ч-ке дейін интегралдап және бастапқы шарттарды ескеріп,
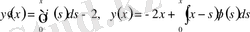
өрнектерін аламыз. Бұл соңғы үш өрнекті теңдеуге қойсақ:
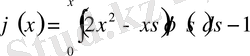
интегралдық теңдеуін аламыз.
2)
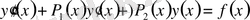 теңдеуін
теңдеуін
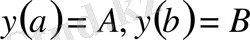 шекаралық шарттарымен қоса қарастыралық. Кәдуілгі дифференциалдық теңдеулер курсында бұл есеп Грин функциясы арқылы:
шекаралық шарттарымен қоса қарастыралық. Кәдуілгі дифференциалдық теңдеулер курсында бұл есеп Грин функциясы арқылы:
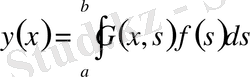
түрінде шешіледі. Егер теңдеудің оң жағы
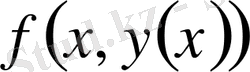 түрінде белгісіз
түрінде белгісіз
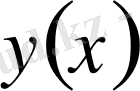 функциясына тәуелді күрделі функция болса, онда соңғы өрнектен:
функциясына тәуелді күрделі функция болса, онда соңғы өрнектен:
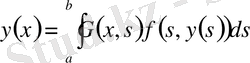
интегралдық теңдеуі шығады. Мәселен,
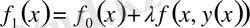 түрінде болса, онда біз сызықтық біртекті емес
түрінде болса, онда біз сызықтық біртекті емес
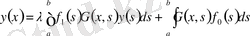
интегралдық теңдеуін аламыз.
3) Кейбір жағдайда интегралдық теңдеуді дифференциалдық теңдеуге келтіріп шешуге болады. Берілген
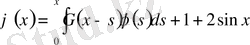
теңдеуін екі рет дифференциалдасақ:
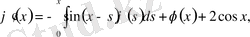
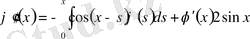
өрнектерін аламыз. Бұлардан
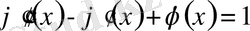 2-ретті дифференциалдық теңдеуі шығады. Жоғарыдағы өрнектерден
2-ретті дифференциалдық теңдеуі шығады. Жоғарыдағы өрнектерден
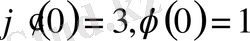 бастапқы шарттары алынады. Демек, интегралдық теңдеуді шешу мәселесі 2-ретті дифференциалдық теңдеуді шешудің Коши есебіне келтірілді.
бастапқы шарттары алынады. Демек, интегралдық теңдеуді шешу мәселесі 2-ретті дифференциалдық теңдеуді шешудің Коши есебіне келтірілді.
Параметр
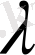 -ға тәуелді
-ға тәуелді
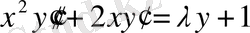 дифференциалдық теңдеуі
дифференциалдық теңдеуі
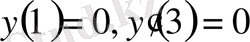 шарттарын қанағаттандыратын шекаралық есепті интегралдық теңдеуге келтірейік. Ол үшін
шарттарын қанағаттандыратын шекаралық есепті интегралдық теңдеуге келтірейік. Ол үшін
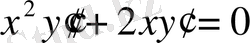 теңдеуінің алдыңғы шарттарды қанағаттандыратын Грин функциясын құрайық. Бұл теңдеудің сызықтық тәуелсіз шешімдері
теңдеуінің алдыңғы шарттарды қанағаттандыратын Грин функциясын құрайық. Бұл теңдеудің сызықтық тәуелсіз шешімдері
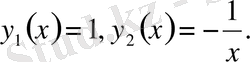 сондықтан Грин функциясын
сондықтан Грин функциясын
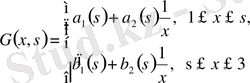
түрінде іздейміз, мұндағы
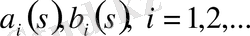 -белгісіз функциялар. Грин функциясының шарттарын пайдалансақ,
-белгісіз функциялар. Грин функциясының шарттарын пайдалансақ,
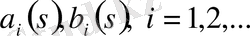 функцияларын төмендегі теңдеулер системасымен анықтаймыз:
функцияларын төмендегі теңдеулер системасымен анықтаймыз:
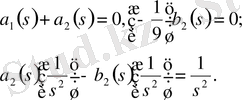
Осы системаны шешіп,
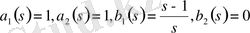 екенін анықтаймыз. Демек,
екенін анықтаймыз. Демек,
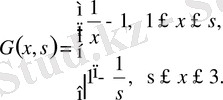
Енді осы өрнекпен анықталған Грин функциясын пайдаланып, берілген дифференциалдық теңдеудің берілген шекаралық шарттарды қанағаттандыратын шешімін табу үшін
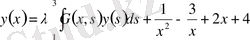
интегралдық теңдеуін аламыз.
Лекция 2
2. ФУНКЦИОНАЛДЫҚ АНАЛИЗДЕН КӨМЕКШІ МАҒЛҰМАТТАР
2. 1. Метрикалық кеңістіктер және онық кейбір қасиеттері.
М сызықтық жиыны берілсін. Оның кез-келген
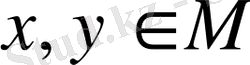 нүктелері пары үшін ара қашықтық немесе метрика ұғымы, оң
нүктелері пары үшін ара қашықтық немесе метрика ұғымы, оң
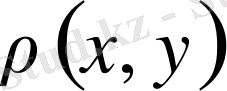 шамасы енгізіліп, ол І
шамасы енгізіліп, ол І
 .
.
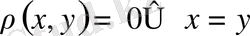 (тепе-теңдік аксиомасы) ; 2
(тепе-теңдік аксиомасы) ; 2
 .
.
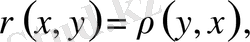
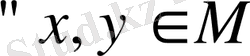 (симметрия аксиомасы) ; 3
(симметрия аксиомасы) ; 3
 .
.
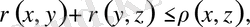
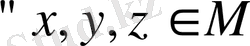 (үшбұрыштар аксиомасы) шарттарын қанағаттандырса, онда жиыны метрикалық кеңістік деп аталады. Бір жиында бірнеше метрика ұғымын анықтап, бірнеше метрикалық кеңістік алуға болады.
(үшбұрыштар аксиомасы) шарттарын қанағаттандырса, онда жиыны метрикалық кеңістік деп аталады. Бір жиында бірнеше метрика ұғымын анықтап, бірнеше метрикалық кеңістік алуға болады.
Мысалдар, 1) арақашықтық
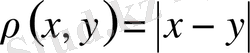 теңдігімен анықталған нақты сандар жиыны Q метрикалық кеңістік болады. Себебі, 1
теңдігімен анықталған нақты сандар жиыны Q метрикалық кеңістік болады. Себебі, 1
 -3
-3
 аксиомалардың Q жиыны үшін орындалатыны айқын.
аксиомалардың Q жиыны үшін орындалатыны айқын.
2) Арақашықтық
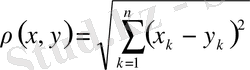
теңдігімен анықталған
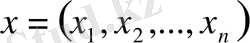 реттелген
n
нақты сандар жиыны метрикалық кеңістік түзеді. Бұл кеңістікті әдетте өлшемді эвклидтік кеңістік беп, оны
реттелген
n
нақты сандар жиыны метрикалық кеңістік түзеді. Бұл кеңістікті әдетте өлшемді эвклидтік кеңістік беп, оны
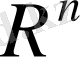 арқылы белгілейді.
арқылы белгілейді.
3)
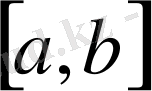 кесіндіде анықталған барлық үзіліссіз функциялар жиыны, егер арақашықтық
кесіндіде анықталған барлық үзіліссіз функциялар жиыны, егер арақашықтық
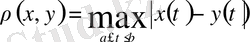 (7)
(7)
теңдігімен анықталса, онда метрикалық кеңістік түзеді.
Шынында да, 1
 мен 2
мен 2
 аксиомалардың орындалатыны оңай байқалады, ал 3
аксиомалардың орындалатыны оңай байқалады, ал 3
 аксиоманы тексерелік.
аксиоманы тексерелік.
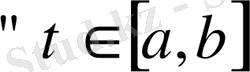 үшін
үшін
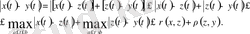
Бұл теңсіздік
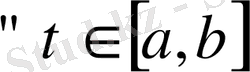 болғандықтан былай жазылады:
болғандықтан былай жазылады:
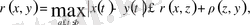
демек 3
 -аксиома деп орындалады. Сонымен арақашықтық (7) өрнегімен анықталған
-аксиома деп орындалады. Сонымен арақашықтық (7) өрнегімен анықталған
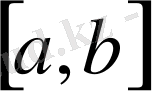 кесіндідегі барлық үзіліссіз функциялар жиыны метрикалық кеңістік түзеді; ол кеңістікті С
кесіндідегі барлық үзіліссіз функциялар жиыны метрикалық кеңістік түзеді; ол кеңістікті С
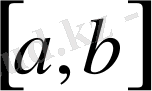 арқылы белгілейді.
арқылы белгілейді.
4)
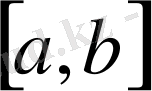 сегментінде квадратымен интегралданатын, яғни
сегментінде квадратымен интегралданатын, яғни
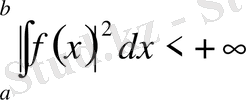
теңсіздігін қанағаттандыратын функциялар жиынын қарастырайық. Арақашықтықты
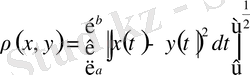 (8)
(8)
формуласымен анықтап, жоғарыдағы аксиомалардың орындалуын тексерейік. Симметрия аксиомасының орынды екені анық. Ал тепе-теңдік аксиомасы
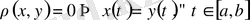 үшін орындалған, яғни өлшемі ноль болатын жиында ғана
үшін орындалған, яғни өлшемі ноль болатын жиында ғана
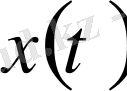 мен
мен
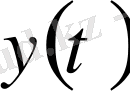 бір-біріне тең емес. Үшбұрыштар аксиомасы Коши-Бундковский теңсіздігінен шығады:
бір-біріне тең емес. Үшбұрыштар аксиомасы Коши-Бундковский теңсіздігінен шығады:
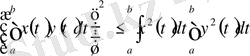 (9)
(9)
Расында, егер (9) теңсіздігін
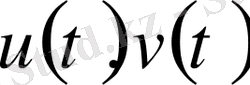 үшін пайдалансақ, онда
үшін пайдалансақ, онда

Бұл өрнектің екі жағынан да квадраттық түбір алсақ
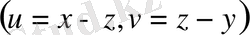 , онда
, онда
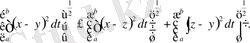
болады, яғни
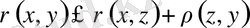 демек үшбұрыштар аксиомасы орынды. Арақашықтық (8) формуласымен анықталғанда
демек үшбұрыштар аксиомасы орынды. Арақашықтық (8) формуласымен анықталғанда
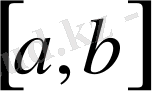 кесінді де квадратымен интегралданатын функциялар жиыны метрикалық кеңістік құрады, оны
кесінді де квадратымен интегралданатын функциялар жиыны метрикалық кеңістік құрады, оны
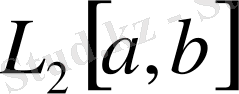 арқылы белгілейді.
арқылы белгілейді.
Метрикалық кеңістіктің элементтерін кеңістіктің нүктелері деп айтады.
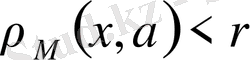 (сәйкес
(сәйкес
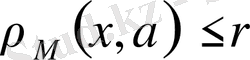 ) теңсіздігін қанағаттандыратын метрикалық М кеңістігіндегі
х
нүктелер жиынын центрі
а
нүктесінде, радиусы
r
болатын шар (тұйық шар) деп айтады да
) теңсіздігін қанағаттандыратын метрикалық М кеңістігіндегі
х
нүктелер жиынын центрі
а
нүктесінде, радиусы
r
болатын шар (тұйық шар) деп айтады да
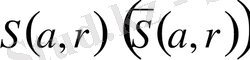 арқылы белгілейді.
арқылы белгілейді.
М - кез-келген метрикалық кеңістік болсын. Егер осы кеңістіктен алынған
 тізбегі үшін
тізбегі үшін
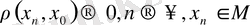 болса, онда
болса, онда
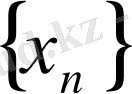 тізбегін
тізбегін
 нүктесіне жинақты тізбек дейді. Егер
нүктесіне жинақты тізбек дейді. Егер
 тізбегі үшін
тізбегі үшін
 санына сәйкес натурал
санына сәйкес натурал
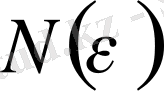 саны табылып, барлық
саны табылып, барлық
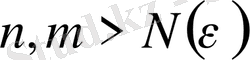 үшін
үшін
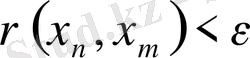 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
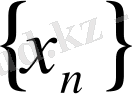 тізбегі өзіне жинақты немесе фундаментальдық тізбек деп аталады.
тізбегі өзіне жинақты немесе фундаментальдық тізбек деп аталады.
Теорема.
Егер
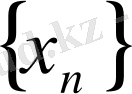 тізбегі
тізбегі
 нүктесіне жинақты болса, онда ол фундаментальды тізбек болады.
нүктесіне жинақты болса, онда ол фундаментальды тізбек болады.
Дәлелдеуі:
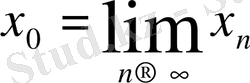 онда
онда
 үшін
үшін
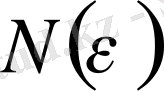 саны табылып,
саны табылып,
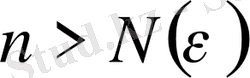 болғанда
болғанда
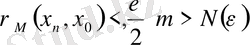 болғанда
болғанда
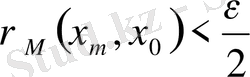 теңсіздігі орындалады. Бұл соңғы екі өрнектен үшбұрыштар аксиомасы бойынша
теңсіздігі орындалады. Бұл соңғы екі өрнектен үшбұрыштар аксиомасы бойынша
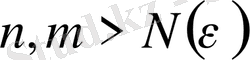 үшін
үшін
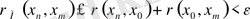 теңсіздігі шығады. Бұл теңсіздіктен анықтамаға сүйеніп
теңсіздігі шығады. Бұл теңсіздіктен анықтамаға сүйеніп
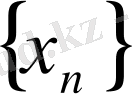 тізбегі фундаментальдық тізбек екеніне көзіміз жетеді.
тізбегі фундаментальдық тізбек екеніне көзіміз жетеді.
Метрикалық кеңістікте жинақты тізбектің шегі сол кеңістіктің элементі болмайтындай тізбектерде кездеседі. Мысалы R - рационал сандар жиыны болсын, мұндағы арақашықтықты
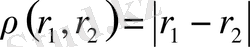 өрнегімен анықтайық. Әрине R метрикалық кеңістік. Енді осы кеңістіктен
өрнегімен анықтайық. Әрине R метрикалық кеңістік. Енді осы кеңістіктен
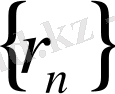 тізбегін қарастыралық, мұнда
тізбегін қарастыралық, мұнда
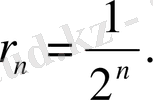 бұл тізбек өзіне және
бұл тізбек өзіне және
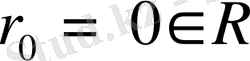 шегіне жинақты. Ал енді жалпы мүшесі
шегіне жинақты. Ал енді жалпы мүшесі
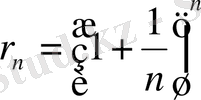
болған тізбекті қарастырсақ, ол өзіне жинақты, бірақ рационал сандар кеңістігінде шекке ие болмайды, себебі
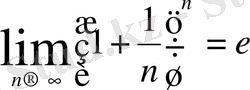
шегі иррационал сан.
Егер метрикалық М кеңістігінің элементтерінен құралған фундаментальдық тізбектің шегі сол кеңістікте жатса, ондай кеңістік толық кеңістік деп аталады. Мысалы, элементтері үзіліссіз функциялар болатын С
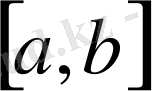 кеңістігі толық. Расында, С
кеңістігі толық. Расында, С
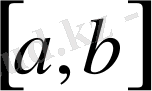 кеңістігінде ұзындық өлшемін
кеңістігінде ұзындық өлшемін
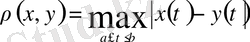 (7)
(7)
формуласымен анықтадық.
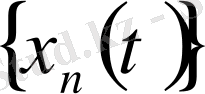 фундаментальдық тізбегі берілсін, мұнда
фундаментальдық тізбегі берілсін, мұнда
 ; тізбек фундаментальдық болғандықтан
; тізбек фундаментальдық болғандықтан
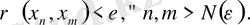 Олай болса,
Олай болса,
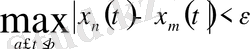
 .
.
Бұл өрнек
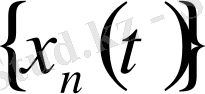 тізбегі үшін
тізбегі үшін
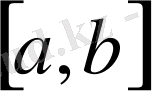 кесіндісіндегі бірқалыпты жинақтылықтың Коши критерийі орынды екендігін көрсетеді.
кесіндісіндегі бірқалыпты жинақтылықтың Коши критерийі орынды екендігін көрсетеді.
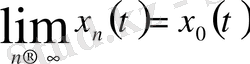 сол тізбектің шегі болсын, демек
сол тізбектің шегі болсын, демек
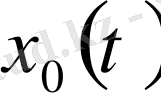 бірқалыпты жинақты үзіліссіз функциялар тізбегінің шегі, олай болса
бірқалыпты жинақты үзіліссіз функциялар тізбегінің шегі, олай болса
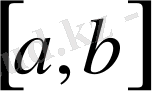 сегментінде үзіліссіз, яғни
сегментінде үзіліссіз, яғни
 және
және
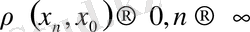 . Демек С
. Демек С
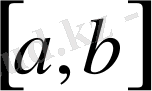 кеңістігі толық.
кеңістігі толық.
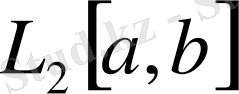 кеңістігі де толық екендігін көрсетуге болады. Нақты сандар жиыны Q ұзындық өлшемі
кеңістігі де толық екендігін көрсетуге болады. Нақты сандар жиыны Q ұзындық өлшемі
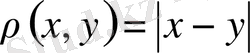 болғанда толық.
болғанда толық.
1-ескерту.
М - метрикалық кеңістік болсын. Кез-келген
 кеңістігі де сол ұзындық өлшемімен метрикалық кеңістік болады.
кеңістігі де сол ұзындық өлшемімен метрикалық кеңістік болады.
2-ескерту.
Егер М - метрикалық кеңістік болса, онда
 кеңістігі толық болмауы мүмкін, бірақ
кеңістігі толық болмауы мүмкін, бірақ
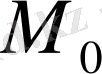 тұйық кеңістік болса, онда ол толық та болады.
тұйық кеңістік болса, онда ол толық та болады.
М мен N - метрикалық кеңістіктер болсын. Егер осы кеңістіктердің нүктелері арасында өзара бірмәнді сәйкестік болып және сәйкес нүктелердің арақашықтығы сақталса, яғни
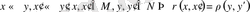 болса, онда М мен N кеңістіктерін изометрикалық кеңістіктер деп атайды. Бір кеңістіктегі изометрикалық екі жиын туралы да айтуға болады. Әрине, изометрикалық кеңістіктердің қасиеттері ұқсас, сондықтан оларды кейде бірдей қасиетті кеңістіктер деп те атайды.
болса, онда М мен N кеңістіктерін изометрикалық кеңістіктер деп атайды. Бір кеңістіктегі изометрикалық екі жиын туралы да айтуға болады. Әрине, изометрикалық кеңістіктердің қасиеттері ұқсас, сондықтан оларды кейде бірдей қасиетті кеңістіктер деп те атайды.
2. 2. Сызықтық нормаланған кеңістік
Егер Е жиын төмендегі шарттарды:
1)
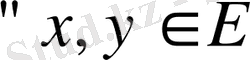 үшін белгілі бір ережемен олардың қосындысы деп аталатын
үшін белгілі бір ережемен олардың қосындысы деп аталатын
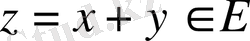 элементі сәйкестендірілсе;
элементі сәйкестендірілсе;
2)
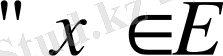 мен
мен
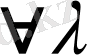 сан үшін белгілі бір ережемен олардың көбейтіндісі деп аталатын элемент
сан үшін белгілі бір ережемен олардың көбейтіндісі деп аталатын элемент
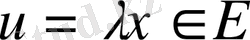 сәйкестендірілсе;
сәйкестендірілсе;
3) сонда: 1
 .
.
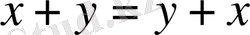 коммутативтік; 2
коммутативтік; 2
 .
.
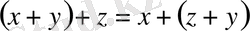 ассоциативтік; 3
ассоциативтік; 3
 .
.
 Ө нольдік элемент және
Ө нольдік элемент және
 ; 4
; 4
 . Әрбір
х
үшін
. Әрбір
х
үшін
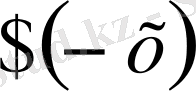 және
және
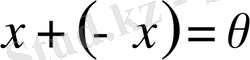 ; 5
; 5
 .
.
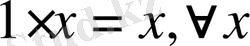 ; 6
; 6
 .
.
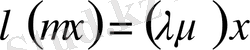 көбейтудің ассоциативтігі; 7
көбейтудің ассоциативтігі; 7
 .
.
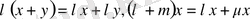 қанағаттандырса, онда Е жиыны сызықтық кеңістік деп аталады. Е жиындағы элементтерді нақты немесе комплекс сандарға көбейтуге байланысты оны нақты немесе комплексті сызықтық кеңістіктерді ажыратады.
қанағаттандырса, онда Е жиыны сызықтық кеңістік деп аталады. Е жиындағы элементтерді нақты немесе комплекс сандарға көбейтуге байланысты оны нақты немесе комплексті сызықтық кеңістіктерді ажыратады.
Мысалдар,
1.
 жиыны векторларды қосу және оларды нақты сандарға көбейту амалдарына қатысты сызықтық кеңістік болады.
жиыны векторларды қосу және оларды нақты сандарға көбейту амалдарына қатысты сызықтық кеңістік болады.
2.
С
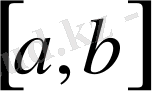 үзіліссіз функциялар жиыны функцияларды қосу және оларды нақты сандарға көбейту амалдарына қатысты сызықтық кеңістік болады.
үзіліссіз функциялар жиыны функцияларды қосу және оларды нақты сандарға көбейту амалдарына қатысты сызықтық кеңістік болады.
Егер Е жиыны
- сызықтық кеңістік болса;
- үшін белгілі бір заңмен солхэлементінің нормасы деп аталатынсаны сәйкес келіп, және мына шарттарды аксиомаларды: 1. тепе-теңдік аксиомасы; 2. - біртектілік аксиомасы; 3. - үшбұрыштар аксиомасы қанағаттандырса, онда-ні сызықтық нормаланған кеңістік деп атайды. сызықтық нормаланған кеңістікте метриканы
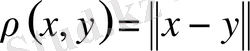 (10)
(10)
теңдігімен анықтауға болады. Міне осы теңдікпен анықталған арақашықтық жоғарыдағы метриканың барлық аксиомаларын қанағаттандаратынына көз жеткізуге болады.
 болғандықтан, (10) өрнегінен
болғандықтан, (10) өрнегінен
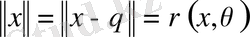 . Демек, кез-келген элементтің нормасы деп сол элементтің нольдік элементке дейінгі қашықтығына тең шаманы алуға болады.
. Демек, кез-келген элементтің нормасы деп сол элементтің нольдік элементке дейінгі қашықтығына тең шаманы алуға болады.
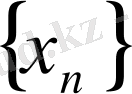 тізбегі үшін
тізбегі үшін
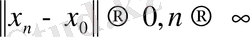 шарты орындалса, онда
шарты орындалса, онда
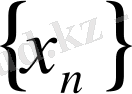 тізбегі
тізбегі
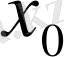 нүктесіне норма бойынша жинақты деп аталады:
нүктесіне норма бойынша жинақты деп аталады:
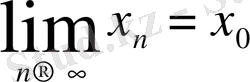 . Егер сызықтық нормаланған кеңістік норма бойынша жинақты және толық болса, онда оны банахтық кеңістік немесе типтегі кеңістік деп атайды.
. Егер сызықтық нормаланған кеңістік норма бойынша жинақты және толық болса, онда оны банахтық кеңістік немесе типтегі кеңістік деп атайды.
Мысалдар,
1.
Элементтерді қосу және санға көбейту операциялары анықталған сызықтық векторлық
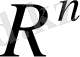 кеңістігін
кеңістігін
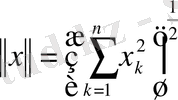 нормасымен В типтегі кеңістікке айналдыруға болады, мүнда
нормасымен В типтегі кеңістікке айналдыруға болады, мүнда
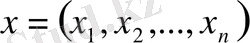 .
.
2.
Егер С
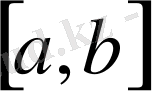 жиынында норманы
жиынында норманы
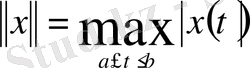 түрінде анықтасақ, В типтегі кеңістік алуға болады.
түрінде анықтасақ, В типтегі кеңістік алуға болады.
3.
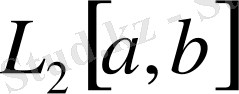 -да
-да
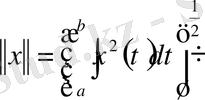 нормасымен В типтегі кеңістік болады.
нормасымен В типтегі кеңістік болады.
4.
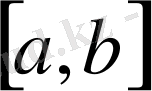 сегментінде үзіліссіз
сегментінде үзіліссіз
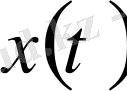 функцияларынан түзілген сызықтық кеңістікті қарастырайық. Бұл кеңістікті
функцияларынан түзілген сызықтық кеңістікті қарастырайық. Бұл кеңістікті
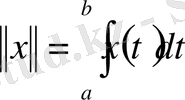 (11)
(11)
нормалы кеңістік етіп алуға болады. Ол кеңістікті
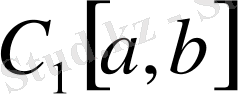 деп белгілейік.
деп белгілейік.
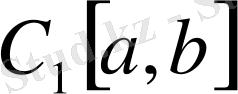 толық кеңістік емес. Мысалы,
толық кеңістік емес. Мысалы,
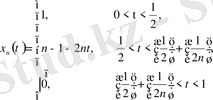
үзіліссіз функциялары тізбегі (11) нормасы бойынша үзілісті
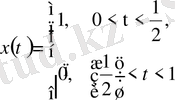
функциясына жинақты. Міне бұл мысалдан біз
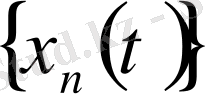 тізбегі
тізбегі
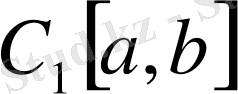 класын фундаментальдық тізбек, бірақ
класын фундаментальдық тізбек, бірақ
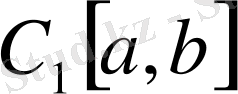 -да оның шегі жоқ, яғни ол толық емес.
-да оның шегі жоқ, яғни ол толық емес.
2. 3. Сызықтық үзіліссіз операторлар
X пен Y - метрикалық кеңістіктер, ал
 болсын. Егер кез-келген
болсын. Егер кез-келген
 элементіне белгілі бір заңдылықпен
элементіне белгілі бір заңдылықпен
 сәйкес қойылса, яғни D-дағы элементтер сызықтық А операторы арқылы Y-тегі
y=Ax
элементтеріне бейнелесе, онда D облысында сызықтық оператор А анықталған дейді. D облысын сызықты А операторының анықталу облысы деп атайды. Егер А операторының әсері мәндерінің жиыны бүкіл Y-пен дәлме-дәл келсе, онда А операторы D-ны Y-ке бейнелейді деп айтамыз.
сәйкес қойылса, яғни D-дағы элементтер сызықтық А операторы арқылы Y-тегі
y=Ax
элементтеріне бейнелесе, онда D облысында сызықтық оператор А анықталған дейді. D облысын сызықты А операторының анықталу облысы деп атайды. Егер А операторының әсері мәндерінің жиыны бүкіл Y-пен дәлме-дәл келсе, онда А операторы D-ны Y-ке бейнелейді деп айтамыз.
Мысалдар,
1.
Х ретінде С
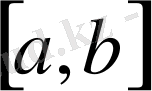 кеңістігін алайық. Әрбір
кеңістігін алайық. Әрбір
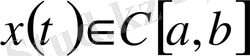 функциясына
функциясына
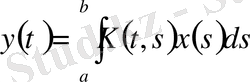
Функциясын сәйкес қойсақ, С
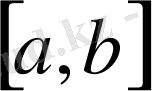 -да анықталған
К
интегралдық фредгольмдік операторын
-да анықталған
К
интегралдық фредгольмдік операторын
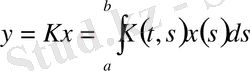
анықтаймыз, мұндағы
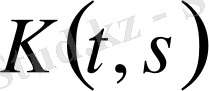 берілген
берілген
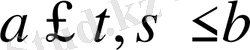 тіктөртбұрышында үзіліссіз функция.
тіктөртбұрышында үзіліссіз функция.
2.
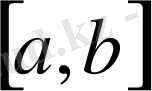 сегментінде ақырсыз дифференциалданатын функциялар жиынын
сегментінде ақырсыз дифференциалданатын функциялар жиынын
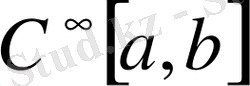 арқылы белгілейік. Әрбір
арқылы белгілейік. Әрбір
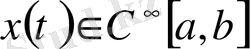 функциясына оның туындысы
функциясына оның туындысы
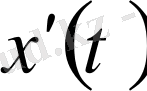 -ны сәйкестендірсек, онда
-ны сәйкестендірсек, онда
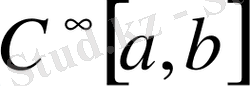 -ны
-ны
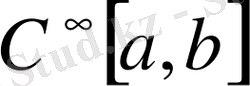 жиынына бейнелейтін дифференциалдау операторы
жиынына бейнелейтін дифференциалдау операторы
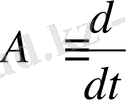 -ны анықтаймыз.
-ны анықтаймыз.
X пен Y сызықтық кеңістіктер болсын. Егер Х-ті Y-ке бейнелейтін А операторы үшін: 1)
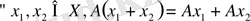 ; 2)
; 2)
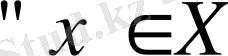 пен
пен
 саны үшін
саны үшін
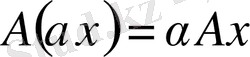 шарттары орындалса, онда А операторы сызықтық оператор деп аталады.
шарттары орындалса, онда А операторы сызықтық оператор деп аталады.
Мысалдар,
1.
Х жиынының кез-келген ақырлы элементін қайтадан өзіне сәйкестендіруші
 өрнегімен берілген І операторы сызықтық оператор болады. Әдетте бұл І операторын бірлік немесе тепе-теңдік оператор деп атайды.
өрнегімен берілген І операторы сызықтық оператор болады. Әдетте бұл І операторын бірлік немесе тепе-теңдік оператор деп атайды.
2.
X=Y=С
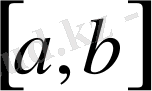 болсын. Үзіліссіз
болсын. Үзіліссіз
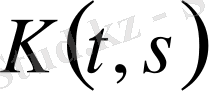 ядролы фредгольмдік интегралдық оператор
ядролы фредгольмдік интегралдық оператор
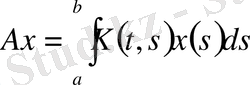 сызықтық және үзіліссіз болатынын дәлелдеу қиын емес.
сызықтық және үзіліссіз болатынын дәлелдеу қиын емес.
X пен Y - сызықтық нормаланған кеңістіктер, ал D(А) кеңістігі Х-ті Y-ке бейнелейтін А операторының анықталу облысы болсын. Егер
 санына сәйкес
санына сәйкес
 саны табылып,
саны табылып,
 нүктелері
нүктелері
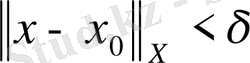 болғанда
болғанда
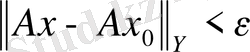 теңсіздігін қанағаттандырса, онда А операторы
теңсіздігін қанағаттандырса, онда А операторы
 нүктесінде үзіліссіз деп айтады.
нүктесінде үзіліссіз деп айтады.
1-теорема.
Сызықты нормаланған Х кеңістігінде анықталған Х-ті Y-ке бейнелейтін және
 нүктесінде үзіліссіз А операторы бүкіл Х кеңістігінде үзіліссіз болады.
нүктесінде үзіліссіз А операторы бүкіл Х кеңістігінде үзіліссіз болады.
Дәлелдеуі.
Х
нүктесі Х жиынының кез-келген элементі болсын және
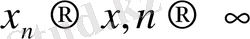 шарты орындалсын. Ол кезде
шарты орындалсын. Ол кезде
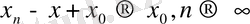 . Ал А операторы
. Ал А операторы
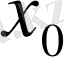 нүктесінде үзіліссіз болғандықтан
нүктесінде үзіліссіз болғандықтан
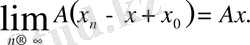
Екінші жағынан А операторының сызықтық болуына байланысты
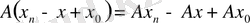 . Сондықтан
. Сондықтан
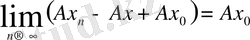 , бұл өрнектен
, бұл өрнектен
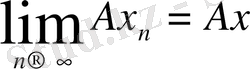 теңдігі шығады. Демек, А операторы
теңдігі шығады. Демек, А операторы
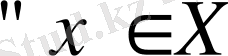 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
Х-ті Y-ке бейнелейтін сызықтық А операторы бүкіл Х-те анықталып,
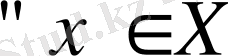 үшін
үшін
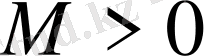 саны табылып,
саны табылып,
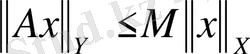 теңсіздігі орындалса, онда А-ны шенелген деп атайды. Сызықтық операторлар арасында олардың шенелгендігі мен үзіліссіздігі тығыз байланыста екенін мына тұжырым көрсетеді.
теңсіздігі орындалса, онда А-ны шенелген деп атайды. Сызықтық операторлар арасында олардың шенелгендігі мен үзіліссіздігі тығыз байланыста екенін мына тұжырым көрсетеді.
2-теорема. Сызықтық А операторы үзіліссіз болуы үшін оның шенелген болуы қажетті де жеткілікті.
Дәлелдеуі.
А - шенелген оператор және
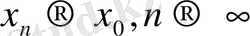 болсын. Сонда, егер
болсын. Сонда, егер
 жағдайда
жағдайда
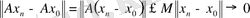 , демек, А үзіліссіз оператор. Енді А - үзіліссіз деп ұйғарайық. Сонда
, демек, А үзіліссіз оператор. Енді А - үзіліссіз деп ұйғарайық. Сонда
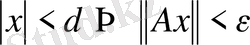 . Егер
. Егер
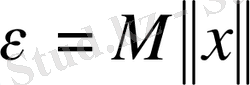 десек, онда
десек, онда
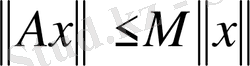 , яғни А - шенелген оператор.
, яғни А - шенелген оператор.
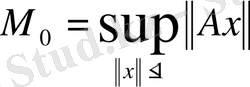
өрнегімен анықталған
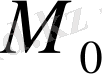 саны А операторының нормасы деп аталады да
саны А операторының нормасы деп аталады да
 символымен белгіленеді.
символымен белгіленеді.
Сызықтық операторлаға амалдар қолдану. Сызықтық нормаланған X пен Y кеңістіктерін және Х-ті Y-ке бейнелейтін А, В, С, . . . сызықтық операторларын қарастырайық.
Егер
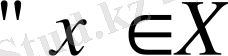 элементі үшін А мен В сызықтық операторлары
элементі үшін А мен В сызықтық операторлары
 теңдігін қанағаттандырса, онда А мен В операторлары бір-біріне тең деп атайды. Сызықтық А операторының скаляр
теңдігін қанағаттандырса, онда А мен В операторлары бір-біріне тең деп атайды. Сызықтық А операторының скаляр
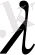 санына көбейтіндісі деп
санына көбейтіндісі деп
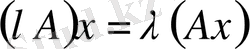 ,
,
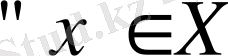 өрнекті қанағаттандыратын
өрнекті қанағаттандыратын
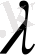 А сызықтық операторын айтады.
А сызықтық операторын айтады.
Х кеңістігінің барлық нүктелері үшін
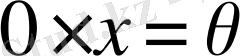 өрнегін қанағаттандыратын сызықтық операторды нольдік оператор деп атап, оны 0 символымен белгілейді. Әрбір сызықтық А операторы үшін әрқашан оған кері оператор деп аталатын -А операторы бар болады, ол
өрнегін қанағаттандыратын сызықтық операторды нольдік оператор деп атап, оны 0 символымен белгілейді. Әрбір сызықтық А операторы үшін әрқашан оған кері оператор деп аталатын -А операторы бар болады, ол
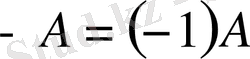 өрнегімен анықталады.
өрнегімен анықталады.
Мына тұжырымның дұрыстығына оңай көз жеткізуге болады. Х-ті Y-ке бейнелейтін операторлар жиыны
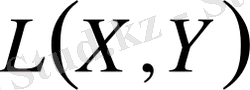 жоғарыдағы операторларды қосу, скаляр санға көбейту, нольдік оператор және кері оператор ұғымдарымен сызықтық кеңістік түзеді. Оның үстіне бұл жиын сызықтық нормаланған кеңістік және ол толық болады.
жоғарыдағы операторларды қосу, скаляр санға көбейту, нольдік оператор және кері оператор ұғымдарымен сызықтық кеңістік түзеді. Оның үстіне бұл жиын сызықтық нормаланған кеңістік және ол толық болады.
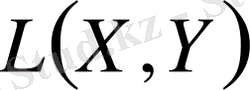 жиындағы сызықтық А мен В операторларының көбейтіндісі деп
жиындағы сызықтық А мен В операторларының көбейтіндісі деп
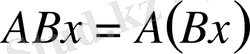 ,
,
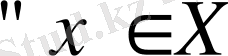 өрнегін қанағаттандыратын АВ операторын айтады. Жалпы жағдайда
өрнегін қанағаттандыратын АВ операторын айтады. Жалпы жағдайда
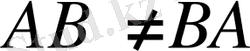 .
.
1-лемма. Сызықтық А мен В операторларының АВ көбейтіндісі де сызықтық оператор болады.
Расында,
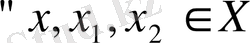 үшін
үшін
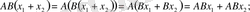
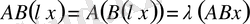 (
(
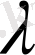 - скаляр) . Демек, 1-лемма дәлелденді.
- скаляр) . Демек, 1-лемма дәлелденді.
Сызықтық операторлар мен скаляр сан
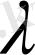 үшін мына өрнектердің дұрыстығын тексеру қиын емес: 1)
үшін мына өрнектердің дұрыстығын тексеру қиын емес: 1)
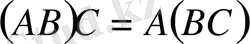 ; 2)
; 2)
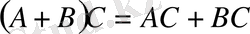 ; 3)
; 3)
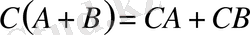 ; 4)
; 4)
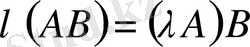 .
.
2-лемма.
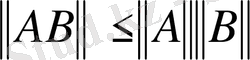 теңсіздігі орындалады.
теңсіздігі орындалады.
Шынында да,
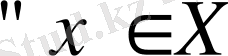 үшін
үшін
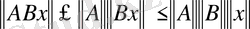 . Демек,
. Демек,
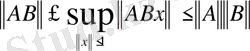 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz