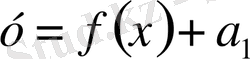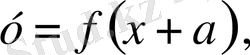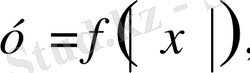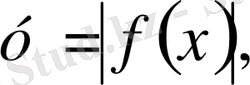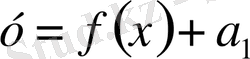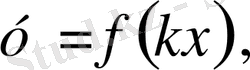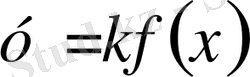Параметрмен берілген есептердің графигін салу

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Параметрмен берілген есептердің графигін салу

Көбінесе, параметрмен берілген тапсырманы шешу әртүрлі геометриялық талдауды қолдану арқылы шешімін оңайлатуға болады, ал қатарда тапсырманың шешімі бір ғана жол арқылы шығарылады. Ең алдымен екі қарапайым мысалмен танысайық.

Мысал 6. 7 параметр а мен берілген теңдеулер жүйесінің қандай мәнінде бір ғана шешім болады.

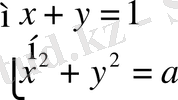
Шешімі: Қойылған шарт бойынша тапсырманы шешу үшін, біз теңдеулер жүйесіне енетін түсіндірудің геометриялық теңдеуін қолданамыз. Теңдеулер жүйесінде берілген нүктелерді (х, у) координата жазықтығында саламыз. Бірінші теңдеулер жүйесінен 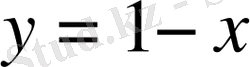түзу сызығы, ал екіншіінен центрі координатаның бас нүктесіне және радиусы 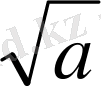-ға тең шеңбер жиыны болады.

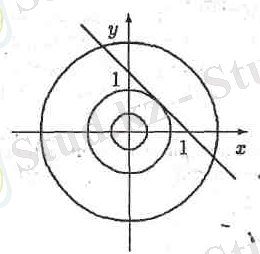
1 суретте көрсетілгендей, берілген жүйенің бір ғана шешім болады. Егер а параметрі шеңберге түзу жанама болғанда, бұл шеңбердің радиусы 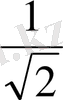оған а -ның мына мәні сәйкес келеді,

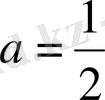
Жауабы :

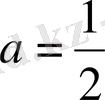
Мысал 6. 8: а параметрімен берілген теңсіздіктің қандай мәнінде барлық х -үзіндісі 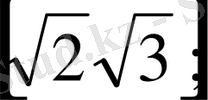-тең болады?

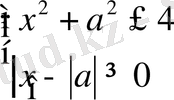
Шешуі: Берілген теңсіздіктер жүйесі бойынша 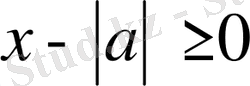шешімін қарастырамыз.

Бірінші теңсіздіктер жүйесінің шешімі центрі координатаның бас нүктесінде және радиусы 2-тең, ал екінші 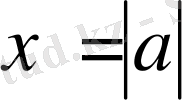функциясының графигінен жоғары жатқан нүктелер.

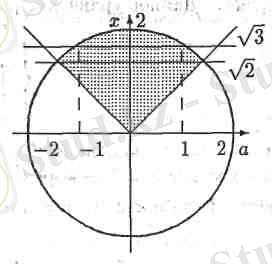
2 суретте берілген нүктелер жүйенің шешмін көрсетеді.

Қойылған шартты формула арқылы келесі жолмен шешуге болады: а -ның мәнін тауып, боялған жолақта жатқан немесе соның 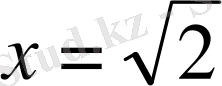және 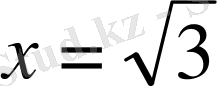түзу сызығын яғни, енді мұндай тапсырманың шешімін табу үшін, х обцисса осімен 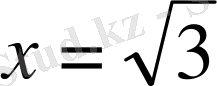шеңберін немесе түзуін кесіп өтетін нүкте табу керек.

Жауабы:

Көрсетілген 2 мысалда аналитикалық жолмен шешілуі мүмкін және бұл шешім әсіресе қиындық келтіретін болмауы да мүмкін. Бірақ, олар параметрмен берілген тапсырмалардың шешімін табуға көп пайдаланылатын 2 басты графикалық әдіс, 6. 7. мысалда берілгендей, (х; у) жазықтығында салынған параметрге тәуелді қисықтар жиыны және белгісіз параметрлер жазықтығында графикалық нұсқасының шешімін салуға болады.

Мысалы (а; х) жазықтығында, 6. 8. мысалда берілгендей.

Сіздерді қарапайым кітаптарда берілген мәліметтер функциялардың графигін салуды үйретпейді. Көбінесе, біз белгісіз, дайын суреттерді қолданамыз. Сондықтан, оқырмандарға өз бетінше параметрден тәуілді графиктер жынын және берілген. Мысалдарға функцияның графигін, қалай салу керек екенін үйренгенін қалаймыз.

Міндетті түрде функцияның графигін салу әдісіне ерекше көңіл бөлуі керек.

Берілген 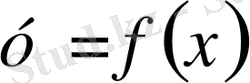функцияның графигін өзгертуге болады.

Мысал. 6. 9. а параметрмен берілгене теңдеулер жүйесінің қандай мәнінде шешімі болады?

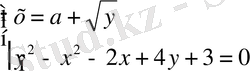
Шешуі: Радикалды оңашалап алып, теңдеулер жүйесіндегі бірінші

теңдеулер жүйесінің екінші жағында квадраттаймыз. Оны біз келесі берілген мына шарт бойынша да қолдана аламыз.

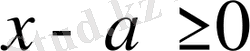
Соныме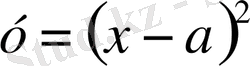н, одан 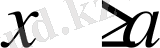шығады. Былайша, бұл теңдеулер жарты пораболаның жиындарын береді. Параболаның оң жақ тармағының 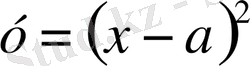ұшы обцииса осімен қиылысады. (3-суретте) . Ары қарай, теңдеулер жүйесінің ІІ бөлігі толық квадрат, оны көбейткішке жіктейміз.

(х, у) жазықтығындағы көптеген нүктелері 2 теңдеуді қанағаттандыратын 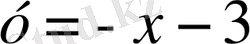және 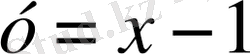түзуі болады. а параметрмен берілген қисықтар жиыны жарты парабола алынған түзулердің ең болмағанда біреуінен тең және бір мән қабылдайтынын анықтаймыз.

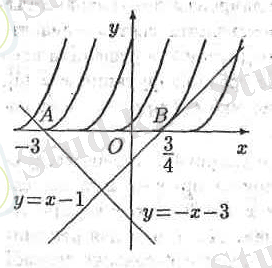
3-суретте көрсетілгендей, егер «жарты параболаның» төбесі А нүктесінің оң жағында бірақ, В нүктесінің сол жағында орналасса, онда қолданылып, отырған графиктеріміз бірдей мән қабылдамайды. Ал, егер «жарты параболаның» төбесі А нүктесімен түйіссе, онда 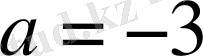болады.

Шартта берілгендей жүйесінің бір ғана шешімі болатынын еске түсіріп, «жарты параболаның» 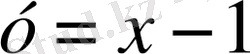түзуімен жанасу нүктесін табамыз.

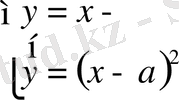
Бұл кезде теңдеу 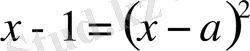бір ғана шешім қабылдайды, осыдан 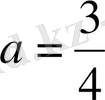шығады. Демек, 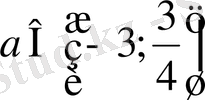арқылы шыққан жүйенің шешімі болмайды, ал параметрінің басқа мәндерінде ең болмағанда бір шешімі болады.

Жауабы: 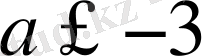немесе

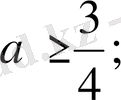
Параметрмен берілген тапсырмаларды жазықтықта зерттеудің тиімді әдісі әдіс аймағында қолданылуы мүмкін. Ол тиімді әді - мағынасы жалпыға бердей, танымал интервалдар әдісі. Оны мысал келтіру арқылы түсіндірейік.

Мысал. 6. 10. Мына теңсіздікте 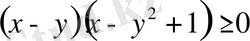қанағаттандыратын (х, у) жазықтығында бірнеше нүктелер қарастырайық.

Шешуі: Берілген теңсіздіктің сол жағын 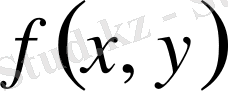арқылы белгілеп алайық.

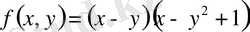
Ең алдымен, нүктенің (х, у) жазықтығында 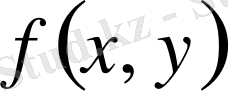0-ге тең болатын геометриялық орнын анықтаймыз. Бұл нүктелерді 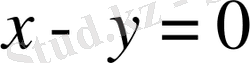және 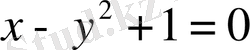теңсіздіктері арқылы өрнектеледі.

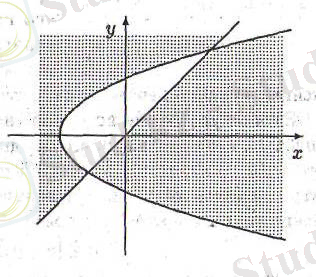
Берілген теңдеулерді обцисса осіне симметриялы біріншісінен - түзу, ал екіншісі - парабола шығады. (4-суретке қара) . Параболамен түзу бүкіл жазықтықты 5-бөлікке бөледі. Және 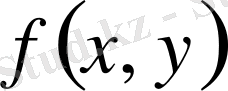функциясы таңбасын ауыстырмайды.

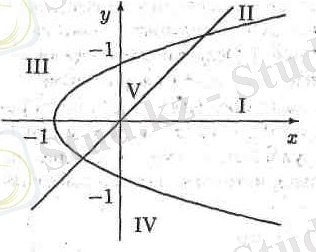
Сондықтан 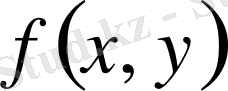функциясының таңбасын, мысалы, І ширекте, осы ширекте жатқан қандай да бір нүкте арқылы 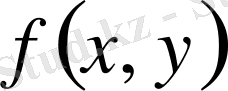функциясының таңбасын анықтауға болады. Кез-келген бір нүктенің координаталарын (1; 0) деп аламыз және функцияның таңбасын анықтаймыз.

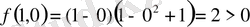
Демек, І ширекте жатқан нүктелердің барлығында функның таңбасы оң, 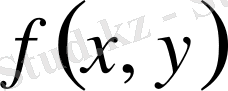функцияның қалған барлық ұқсас ширектерінде таңбасы анықталады. Бұны өздеріңіз өз бетімен тексеріп көріңіздер. Бұл есептің