Ақпаратты қорғаудың криптографиялық негіздері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:
АҚПАРАТТЫ ҚОРҒАУ МӘСЕЛЕСІНІҢ КРИПТОГРАФИЯЛЫҚ НЕГІЗДЕРІ
МАЗМҰНЫ
КІРІСПЕ 3
1 КРИПТОГРАФИЯНЫҢ МАТЕМАТИКАЛЫҚ НЕГІЗДЕРІ 4
1. 1 Модулярлық арифметиканы есептеу 4
1. 2 Дәрежеге шығару алгоритмі 5
1. 3 Эйлер функциясы 7
1. 4 Модулярлық арифметикада кері шамаларды есептеу 10
1. 4. 1 Тура іріктеу әдісі 12
1. 4. 2 Эйлер функциясы көмегімен кері шамаларды есептеу 12
1. 4. 3 Евклидтің кеңейтілген алгоритмі көмегімен кері шамаларды есептеу 13
2 ШИФРЛЕУ АЛГОРИТМДЕРІ 17
2. 1 Симметриялық алгоритмдер 17
2. 1. 1 Блоктық шифрлар 18
2. 1. 2 Ағындық шифрлар 31
2. 1. 3 Құрама шифрлар 32
2. 2 Ассиметриялық алгоритмдер 32
2. 2. 1 RSA алгоритмі 33
2. 2. 2 Диффи - Хеллман алгоритмі 36
2. 2. 3 Эль-Гамаль алгоритмі 40
3 АШЫҚ КІЛТТІ КРИПТОЖҮЙЕДЕ КІЛТ БАСҚАРУ 42
3. 1 Сертификация 42
3. 2 PGP қауіпсіз электрондық поштасы 44
4 ПРАКТИКАЛЫҚ ЖҰМЫС 47
ҚОРЫТЫНДЫ 51
ӘДЕБИЕТТЕР ТІЗІМІ 52
ҚОСЫМША А 54
Кіріспе
Қазіргі кезде ақпаратты қорғау жалпы ұлттық мәселеге айналып отыр. Информациялық технологияның қарқынды дамуы және Интернеттің тез таралуы конфиденциалды ақпаратты қорғаудың әдістерін дамытуға, әсіресе криптографияның дамуына көп әсер етті.
Мемлекеттің барлық салаларына қатысты ақпарат нақты саяси, материалдық және бағалылығы жағынан да құнды болып саналады. Ақпаратты қорғау мемлекеттің көзқарасымен алғанда қазіргі кезде өзекті мәселеге айналды және мемлекет алдындағы бірден-бір шешілуі қажет, ұлттық қауіпсіздіктің негізгі элементі ретінде қарастырылып отыр.
Жаңа қуатты компьютерлердің, желілік технологиялардың пайда болуы мен ақпараттың компьютерде шоғырлануы мүлдем ашылмайды деп саналған криптография жүйесін пайдалануға мүмкіндік береді.
Криптография термині ежелгі гректердің «cryptos - құпия» және «grapho - жазу» сөздерінен құралған.
Бітіру жұмысымның мақсаты:
- ақпараттық ресурстардың сыртқа кетуін, ұрлануын, жоғалуын, бұрлануын, қолдан жасалуын, оларға рұқсатсыз қол жеткізуді пайдалануды және таратуды, зиян, залал келтіруді болғызбау;
- тұлғаның, мемлекеттің және қоғамның ақпараттық қауіпсіздігі;
- ақпаратты қорғаудың математикалық жолдарын (яғни, математикалық әдістерін немесе қулықтарын) және ақпаратты қорғаудың математикалық мәселелерін шешу;
- математиканы және жалпы білімді дәріптеу.
Бітіру жұмысымның өзектілігі. Криптография қоғам өмірінің ажырымас бөлігіне айналып келеді. Мыңдаған жылдар бойы криптография әскери және дипломатикалық байланыстарды қорғау үшін қолданылып келеді. Информациялық ғасырдың басталуымен бірге криптографияның жеке секторлары да қоғамға жедел қажет екендігін байқалтты.
Ақпаратты қорғаудың әртүрлі жолдары (мысалы, механикалық немесе физикалық), әртүрлі мәселелері бар (мысалы, қоғамдық немесе әскери) . Мен ақпаратты қорғаудың математикалық жолдарын (яғни, математикалық әдістерін немесе қулықтарын) және ақпаратты қорғаудың математикалық мәселелерін қарастырамын.
Бітіру жұмысымның міндеттері. Ақпаратты қорғау әдістері мен ақпаратты шифрлеу жүйелері жайлы мағлұмат беру. Сонымен қатар криптографияның математикалық негіздері болып табылатын симметриялық және ашық кілтті криптожүйелер туралы ашып айту. Ашық кілтті криптожүйеде кілт басқару қалай жүзеге асатынын көрсету. 1 КРИПТОГРАФИЯНЫҢ МАТЕМАТИКАЛЫҚ НЕГІЗДЕРІ
1. 1 Модулярлық арифметиканы есептеу
Модулярлық арифметика көбінде жай арифметикаға ұқсас: ол коммутативті, қауымдастықты, дистрибутивті. Толығырақ айтатын болсақ, қосу мен көбейту операцияларын қолданатын n модулі бойынша бүтін сандар коммутативті, қауымдастықты, дистрибутивті заңдарын қолдай отырып, коммутативтік сақина құрайды.
Негізінен модулярлық арифметиканың жазылуы төмендегідей түрде:
а ≡ b (mod n), бұл «n модулі бойынша а және b сандары салыстырмалы» деп оқылады.
Бұл ара қатынас бүтін мәндер а, b және n ≠ 0, егер а = b + k*n (кейбір к бүтін сандарына) үшін тура.
Бұдан шығатыны n (a-b), бұл «n (a-b) -ға бөлінеді» деп оқылады.
Егер бұл қатынас орындалса, онда b санын n модулі бойынша а-ның шегеру саны деп аталады. Шегеру санын табу операциясын модуль бойынша келтіру деп аталады.
Анықтама 1 Егер a-b айырымы n-ге қалдықсыз бөлінетін болса а және b бүтін сандарын n модулі бойынша салыстырмалы деп аталады.
0-ден n - 1-ге дейінгі бүтін сандардың жиынтығын n бойынша модулін шегеруінің толық жиынтығы деп атайды.
n = 7, { 0, 1, …, 6 }
n = 100, { 0, 1, …, 99 }.
Дұрысы біз алдымен n модулі бойынша шығарып алып, содан операцияны орындауымызға болады немесе алдымен операцияны, содан кейін n модулі бойынша шығаруға мүмкін болады:
(a+b) mod n = ((a mod n) + (b mod n) ) mod n
(a-b) mod n = ((a mod n) - (b mod n) ) mod n
(a*b) mod n = ((a mod n) * (b mod n) ) mod n
(a*(b+c) ) mod n = (((a*b) mod n) + ((a*c) mod n) ) mod n
Дискреттiк логарифм және түбiр квадратын есептеу қиын болғандықтан, криптография n модулi бойынша көптеген есептер қолданылады. Сонымен қатар, модуль бойынша есептеулермен жұмыс iстеу тиiмдiрек, өйткенi олар барлық аралық өлшем мен нәтиженiң диапазоның шектейдi.
Анықтама 2 Модулі бойынша белгілі бір а санымен салыстырмалы сандардың жиыны сынып деп аталады. Ол
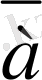 деп белгіленеді.
деп белгіленеді.
Мысал: 6 модулі бойынша
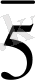 сыныбы:
сыныбы:
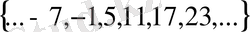
Модулярлық арифметиканы компьютерлік есептеулерге қолдану үшін біз тек қана шектелген мәндер диапазонын қарастыруымыз керек. Сондықтан негізінен
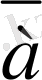 сыныбындағы ең кіші оң санымен жұмыс істейді. Сандар теориясында мұндай санның бар екендігі және де ол а-ны n-ге бөлгендегі қалдыққа тең екендігі дәлелденген.
сыныбындағы ең кіші оң санымен жұмыс істейді. Сандар теориясында мұндай санның бар екендігі және де ол а-ны n-ге бөлгендегі қалдыққа тең екендігі дәлелденген.
Ескерту. Программалау тілдерінде mod функциясы басқаша анықталуы мүмкін.
Модулярлық арифметиканың артықшылығы:
- Бүтін сандармен жұмыс істейміз;
- Есептердің барлық нәтижелері супер өрісте орналасқан.
Мысалы. 13 mod 7 = 6, 0≤n≤n-1
7 mod 7 = 0, 4 mod 7 = 4, -1 mod 7 = 6.
1. 2 Дәрежеге шығару алгоритмі
К биттi ұзындықты n модулiнiң қосу, алу немесе көбейту сияқты аралық нәтижелері 2к биттен ұзын болмайды. Сондықтан модулярлық арифметикада дәрежеге шығаруды өте үлкен аралық нәтижелердің генерациясынсыз орындауға болады.
n модулi бойынша а санының дәрежесiн есептеудi a x mod n kөбейту мен бөлудiң қатары ретiнде орындауға болады. Бұны тездету үшiн неше түрлi әдiстерi бар. Бұл операциялар дистрибутивтi болғандықтан, модуль бойынша келтiрудi әркез орындай отырып, көбейту қатары ретiнде дәрежеге шығаруды тездетiп орындау. Егер ұзын сандармен (200 бит және одан да көп) жұмыс жасаса, бұл ерекше белгiлi болады.
Мысалы, егер a 8 mod n -дi есептеу керек болса, жетi рет қайта көбейту мен модуль бойынша үлкен санды бiреуге келтiруге (a*a*a*a*a*a*a) mod n примитивтi жақындау қолданып керегi жоқ.
Бұның орнына 3 кiшi көбейту мен 3 кiшi модуль бойынша келтiру орындалады:
((a 2 mod n) 2 mod n) 2 mod n
Осы әдiспен a 16 mod n = (((a 2 mod n) 2 mod n) 2 mod n) 2 mod n есептелiнедi.
Есептеу бiраз ғана қиынырақ: a x mod n (4), мұндағы x 2-дәрежелі болып табылмайды. x cанының екiлiк жазуы x санын 2-дәрежелердiң қосындысы ретiнде келтiрудi қолдайды:
x
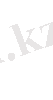 = 25
(10)
→ 1 1 0 0 1
(2)
, сондықтан 25 = 2
4
+ 2
3
+ 2
0
тең болады.
= 25
(10)
→ 1 1 0 0 1
(2)
, сондықтан 25 = 2
4
+ 2
3
+ 2
0
тең болады.
Онда a 25 mod n = (a*a 24 ) mod n = (a*a 8 *a 16 ) mod n = a*((a 2 ) 2 ) 2 *(((a 2 ) 2 ) 2 ) 2 mod n = a 2 *a) 2 ) 2 ) 2 *a) mod n деп аламыз.
Аралық нәтижелерде алты ғана көбейту амалы керек болады:
a 2 mod n) *a) mod n) 2 mod n) 2 mod n) 2 mod n) *a) mod n
Бұл әдiс 1, 5хк операциясына дейiн есептеуде қиындықты жеңiлдетедi, мұндағы к - бит негiзiндегі сандар ұзындығы.
Көптеген шифрлеу алгоритмi n модулi бойынша дәрежеге шығаруға негiзделген болғандықтан, тез дәрежеге шығару алгоритмiн қолдану орынды.
S = a W mod n мағынасын есептеу керек болсын. W дәрежесін 2 санын дәрежеге үлестіру түрінде келтіреміз:
W = w g-1 2 g-1 + w g-2 2 g-2 + … + w 2 2 2 + w 1 2 1 + w 0
мұндағы w i 0 немесе 1сандары.
S = a W mod n - ді келесі түрде келтірейік:
S = a
w
mod n =
 a
W
g-1
2
a
W
g-1
2
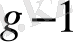 + W
g-2
2
+ W
g-2
2
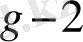 + … + W
2
2
+ … + W
2
2
 + W
1
2
+ W
1
2
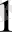 + W
0
mod n = (a
2
)
W
g-1
2
+ W
0
mod n = (a
2
)
W
g-1
2
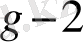 +
W
g-2
2
+
W
g-2
2
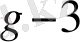 + … + W
2
2
+ … + W
2
2
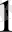 + W
1
2
+ W
1
2
 *a
w
0
mod n = ((a
2
)
2
)
W
g-1
2
*a
w
0
mod n = ((a
2
)
2
)
W
g-1
2
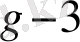 + W
g-2
2
+ W
g-2
2
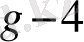 + … + W
2
2
+ … + W
2
2
 *(a
2
)
W
1
*a
W
0
mod n = ( …((a
2
)
2
… )
2
)
W
g-1
* … *(a
8
)
W
3
*(a
4
)
W
2
*(a
2
)
W
1
*a
W
0
mod n.
*(a
2
)
W
1
*a
W
0
mod n = ( …((a
2
)
2
… )
2
)
W
g-1
* … *(a
8
)
W
3
*(a
4
)
W
2
*(a
2
)
W
1
*a
W
0
mod n.
Мысалдар:
1) 4 37 mod 26 = ((4 2 ) 19 - 4) mod 26 = [(16 mod 26) 19 - 4] mod 26 = (16 2 ) 9 *4 mod 26 - 4 = (256 mod 26) 9 *4 mod 26 - 4 = 22 9 *4 mod 26 - 4= (22 2 ) 4 *22*4 mod 26 - 4 = (484 mod 26) 4 *22*4 mod 26 = (16) 4 *22*4 mod 26 = (16 2 ) 2 *22*4 mod 26 = 22 2 *22*4 mod 26 = 16*22*4 mod 26 = 16*88 mod 26 = 16*10 mod 26 = 160 mod 26 = 4.
2) [(2 23 mod 11) 39 + (4 11 mod 7) 19 ] mod 11
- (223mod 11) 39= ((24) 5*23mod 11) 39= (55*23mod 11) 39= ((52) 2*5*23mod 11) 39= (32*5*23mod 11) 39= (45*23mod 11) 39= 839
- (411mod 7) 19= ((42) 5*4 mod 7) 19= (25*4 mod 7) 19= (23*22*4 mod 7) 19= (16 mod 7) 19= 219
- 839mod 11 + 219mod 11 = (82) 19*8 mod 11 + (24) 4*23mod 11 = (9) 19*8 mod 11 + 54*23mod 11 = (92) 9*9*8 mod 11 + (52) 2*23mod 11=49*9*8 mod 11 + 32*23mod 11 = (42) 4*4*9*8 mod 11 + 32*23mod 11 = (52) 2*4*9*8 mod 11 + 6 = 32*4*9*8 mod 11 + 6 = 3*9*8 mod 11 + 6 = 5*8 mod 11 + 6 = 7+6 = 13
- 13 mod 11 = 2.
1. 3 Эйлер функциясы
Айталық, m = p 1 α 1 p 2 α 2 … p t α t , m>1 натурал санының Канондық жіктелуі болсын.
φ (m) = p 1 α 1 -1 (p 1 -1) p 2 α 2 -1 (p 2 -1) … p t α t -1 (p t -1) және φ(1) = 1 болсын.
Сонымен натурал аргументті φ функциясын анықтаймыз.
Анықтама 1 Жоғарыда көрсетілген әдіспен анықталған φ функциясы Эйлер функциясы деп аталады.
Анықтама 2 Эйлер функциясы n-нан кіші және n-мен өзара жай оң бүтін сандардың санына тең функцияны атайды. Функция φ(n) деп белгіленеді.
Мысалға, φ (10) = 4. Эйлер функциясының келесі тамаша қасиеті бар: егер n = pq, мұндағы p және q - жай сандар, онда φ(n) = (p-1) (q-1) -ге тең болады.
Теорема 1 (Эйлер) Кез-келген n модулі мен n-мен өзара жай а саны үшін келесі салыстыру ақиқат
a φ(n) -1 ≡ 1(mod n)
Анықтама 3 Келесі үш шартты қанағаттандыратын θ функциясын мультипликативті деп атаймыз:
- θ кез келген натурал сан үшін анықталған;
- θ(1) = 1;
- егер (a, b) = 1 болса, онда θ(ab) = θ(a) θ(b) .
Теорема 2 Эйлер функциясы - мултипликативті функция.
Дәлелдеуі. Айталық, p 1 α 1 … p t α t және q 1 β 1 … q s β s сәйкесінше өзара жай натурал m 1 >1 және m 2 >1 өзара жай сандарының канондық жіктеулері болсын. Онда p 1 , …, p t сандарының әрқайсысы q 1 , …, q s сандарының әрқайсысына өзгеше. Бұдан m 1 m 2 канондық жіктеуі p 1 α 1 … p t α t q 1 β 1 … q s β s . φ (m 1 m 2 ) = φ (m 1 ) φ (m 2 ) теңдеуі, Эйлер функциясының анықтамасынан тікелей шығады. m 1 = 1 немесе m 2 = 1 үшін берілген теңдеу айқын. Теорема дәлелденді.
Теорема 3 φ (m) саны 1, 2, …, m сандық тізбегіндегі m-мен өзара жай болатын сандардың санына тең.
Дәлелдеуі. Дәлелдеме m>1 санының канондық жіктеуіндегі жай көбейткіш сандардың саны n бойынша математикалық индукция әдісі бойынша жүргізіледі. Теорема n = 0 (m = 1) және n = 1 (m = p) үшін орындалады, мұндағы p - жай сан. Айта кетерлік жайт, i натурал саны mp-мен өзара жай болу үшін ол бір мезгілде m мен p сандарымен өзара жай болуы қажет және жеткілікті. 1, 2, …, mp тізбегін талдау үшін ұзындығы m-ге тең p тізбекшелеріне m k+1 , m k+2 , …, m k+m -бөлеміз, мұнда k = 0, 1, …, p-1. Теорема 3-тен (mk + i, m) = (i, m) шығады. Осы теңдік пен осы индуктивті ұйғарымнан m k+1 , m k+2 , …, m k+m тізбекшесінде m-мен өзара жай φ (m) сан бар. Осыдан 1, 2, …, mp тізбегінде m-мен өзара жай φ (m) p сан бар. M p-ға бөлінетін жағдайда, бұл сандар p-мен өзара жай, сонымен қатар mp санымен де өзара жай. Соңғы ескерту мен айқын теңдік φ (mp) = φ (m) p қарастырылған жағдайдағы теореманың ұйғарымын дәлелдейді.
m-нің p-ға бөлінбейтін жағдайын қарастыру қалды. m-мен өзара жай φ (m) p сандарының санынан осылардың p-ға бөлінетіндерінің санын алып тастасақ, іздеген φ (mp) санын табамыз. Ол сандар тек p, 2p, 3p, …, mp сандарының арасында ғана болуы мүмкін. Сондықтан, m-мен өзара жай сандардың арасындағы p-ға бөлінетіндерінің саны p, 2p, 3p, …, mp сандарының арасындағы m-мен өзара жай сандардың санына тең болады. Егер i≤m және (m, p) = 1 болғанда (ip, m) = (i, m) болатынын ескерсек, онда p, 2p, 3p, …, mp сандарының арасындағы m-мен өзара жай сандар саны. 1, 2, …, m сандарының арасындағы m-мен өзара жай сандар санына тең, яғни индукция бойынша φ (m) . Қорыта келе, ізделінді φ (mp) = φ (m) p - φ (m) = φ (m) (p-1) . Теорема дәлелденді.
Эйлер функциясының осы қасиетінің берілген дәлелдемесін Р. А. Сүйіндіков ұсынды.
Мысалдар: Берілген n натурал саны жай сан деп саналады, егер де ол тек өзіне ғана және 1-ге бөлінетін жағдайда a, n 2 натурал сандар өзара жай сандар деп саналады, егер олардың ортақ бөлгіштері болмаса.
1. n = 7
1 2 3 4 5 6 ϕ(7) = 6.
2. n = p*q, p, q -жай сандар, ϕ(n) = (p-1) *(q-1)
n = 33 = 11*3, ϕ(33) = (11-1) (3-1) = 20.
3. n = k r
ϕ(n) = (k-1) *k r-1 , n = 8 = 2 3
ϕ(8) = (2-1) *2 3-1 = 1*4 = 4.
1. 4 Модулярлық арифметикада кері шамаларды есептеу
Нақты сандарды арифметикада а
-1
мультипликативтi керi шаманы есептеу қиынға түспейдi. Нөлдiк емес а үшiн: a
-1
=
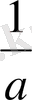 Equation. 3 немесе а*а
-1
= 1 деп есептейміз.
Equation. 3 немесе а*а
-1
= 1 деп есептейміз.
Мысалы, мультипликативтi керi шама 4 санынан ¼-ке тең, өйткенi 4*
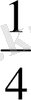 = 1-ге тең болғандықтан.
= 1-ге тең болғандықтан.
Ал модулярлық арифметикада керi шаманы есептеу қиын есеп болып табылады. Мысалы, салыстыруды есептеу 4*x ≡ 1 (mod 7) х және к мәндерiн табумен эквиваленттi, бұл 4*х ≡ 7*к + 1-ге тең, мұндағы х және к - бүтiн сандар.
Бұл есептiң жалпы тұжырымы - х бүтiн санын табу, бұл дегенiмiз a*x (mod n) = 1, басқаша осылай a -1 ≡ x (mod n) деп жазуға болады.
Бұл есептiң шешiмi кейде болады, кейде болмайды. Мысалы, 14 модулi бойынша 5 саны үшiн керi шама 3-ке тең, өйткенi
5*3 = 15 ≡ 1 (mod 14)
Келесi жақтан қарасақ, 14 модулi бойынша 2 санында керi шама жоқ.
Егер а және n - өзара жай сандар болса, жалпы a -1 ≡ x (mod n) салыстыруында бiр ғана нәтиже бар, .
Егер а және n сандары өзара жай сандар болмаса, онда салыстыру a -1 ≡ x (mod n) тең болады.
Нәтижесi жоқ керi шаманы табудың негiзгi әдiсiн тұжырымдаймыз. a
 {0, 1, 2, …, n-1} бүтiн сандар болсын. Егер ЕҮОБ(a, n) = 1, онда a*i (mod n), мұндағы i = 0, 1, 2, …, n-1, {0, 1, 2, …, n - 1}жиынтығын алмастыру болып табылады.
{0, 1, 2, …, n-1} бүтiн сандар болсын. Егер ЕҮОБ(a, n) = 1, онда a*i (mod n), мұндағы i = 0, 1, 2, …, n-1, {0, 1, 2, …, n - 1}жиынтығын алмастыру болып табылады.
Мысалы, егер a = 3 және n = 7 (ЕҮОБ(3, 7) = 1), онда 3*i (mod 7), мұндағы i = 0, 1, 2, …, n-1; 0, 3, 6, 2, 5, 1, 4 жүйелiк болып табылады., яғни {0, 1, 2, …, 6}жиынтығын алмастыру болып табылады.
Егер ЕҮОБ(a, n) ≠ 1 болса, жоғарыда келтірілген мысал дұрыс емес болып шығады. Мысалы, егер a = 2 және n = 6 болса, онда 2*i (mod 6) ≡ 0, 2, 4, 0, 2, 4 мұндағы i = 0, 1, 2, …, 5 болады.
Егер ЕҮОБ(a, n) = 1, онда a -1 керi сан бар болады және де дәл осындай түрде болады:
a*a -1 ≡ 1 (mod n)
Шындығында да, a*i (mod n) 0, 1, …, n-1 алмастыруы болып табылады, сондықтан i бар болады және төмендегідей түрде болады:
a*i ≡ 1 (mod n)
Мысалы, n = 11-жай сан болсын. 11 модуль бойынша шегерудiң толық жиыны {0, 1, 2, …, 10}.
Келтiрiлген шегеру жиынын тұжырымдаған кезде олардың iшiнен бiр ғана элемент - 0 өшiрiледi. Келтiрiлген шегеру жиыны 11 модулi бойынша 11-1 = 10 элементi бар болады.
Жалпы келтiрiлген шегеру жиынында n модуль бойынша жай санының n-1 элементi бар болады.
Эйлер функциясы φ(n) шегеру жиынтығында келтірілген элементтер санын мінездейді. Төмендегі кестеден көруге болады.
Кесте 1 Эйлер функциясы
N - жай сан
n2
·
·
·
n r
n-1
n(n-1)
·
·
·
n r-1 (n-1)
P*q (p, q - жай сандар)
·
·
·
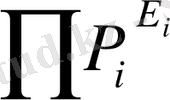 (p- жай сан)
(p- жай сан)
(p-1) (q-1)
·
·
·
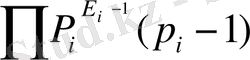
Басқаша айтқанда, Ферманың кiшкене теоремасы: егер n-жай және ЕҮОБ(a, n) = 1, онда a n-1 ≡ 1 (mod n) болады.
Эйлердiң қортуына сәйкес Ферманың кiшене теоремасынан: eгер ЕҮОБ(a, n) = 1, онда a φ(n) ≡ 1 (mod n) -ге тең.
Керi шаманы табудың негiзгi 3 әдiсі бар. Олар: тура іріктеу әдісі, евклидтің кеңейтілген алгоритмі көмегімен кері шамаларды есептеу әдісі, Эйлер функциясы көмегімен кері шамаларды есептеу әдісі. Соларға тоқталайық.
1. 4. 1 Тура іріктеу әдісі
a -1 ≡ 1 (mod n) табылмағанға дейiн, осындай a*a -1 (mod n) ≡ 1 теңдікті 1, 2, …, n-1 кезектi мәндерiн қою арқылы тексеру.
Мысалға, x = a -1 (mod n) табылмағанға дейiн, 1, 2, …, n-1 кезектi мәндерiн тексеру, осындай a*x ≡ 1 (mod n) түрде болады.
n = 7, ал a = 5 болсын. x = a -1 (mod n) -дi табу керек.
а*x ≡ 1 (mod n) немесе 5*х ≡ 1 (mod 7) .
n - 1 = 7 - 1 = 6
x = 5 -1 (mod 7) = 3 - тi аламыз.
Кесте 1 Тура іріктеу әдісінің мысалы
1
2
3
4
5
6
5
10
15
20
25
30
5
3
1
6
4
2
1. 4. 2 Эйлер функциясы көмегімен кері шамаларды есептеу
Eгер Эйлер φ(n) функциясы белгiлi болса, онда дәрежеге тез шығару алгоритмiн қолдана отырып a -1 (mod n) ≡ a φ(n) - 1 (mod n) табуға болады.
Кесте 1 Эйлер функциясы көмегімен кері шамаларды есептеу
n
n 2
n r
n-1
r(n-1)
n r-1 (n-1)
Егер а және n өзара жай сандар болса, a
-1
 x(mod n) салыстырылуы бір ғана есептеуін қажет етеді. Егер а және n өзара жай сандар болмаса, онда бұл салыстыру есептеуді қажет етпейді.
x(mod n) салыстырылуы бір ғана есептеуін қажет етеді. Егер а және n өзара жай сандар болмаса, онда бұл салыстыру есептеуді қажет етпейді.
Егер Эйлер функциясы белгілі болса, онда кері шаманы есептеуге болады:
а -1 (mod n) = a φ(n-1) (mod n)
Мысалдар:
- a-1(mod n) -дi табу керек, егер Эйлер φ(n) функциясы белгiлi болса.
n = 7, ал a= 5 болсын. x = a -1 (mod n) = 5 -1 (mod 7 ) -нi табу керек.
n = 7 модулi - жай сан. Сондықтан Эйлер функциясы φ(n) = φ(7) = n-1 =6.
Керi шама 5-тен 7 - ге дейiнгі аралықты қамтиды.
a -1 (mod n) = a φ(n) - 1 (mod n) = 5 6-1 mod 7 = 5 5 mod 7 = (5 2 mod 7) (5 3 mod 7) mod 7 = (25 mod 7) (125 mod 7) mod 7 = (4*6) mod 7 = 24 mod 7 = 3.
Нәтижесі x = 5 -1 (mod 7) = 3-ке тең.
1. 4. 3 Евклидтің кеңейтілген алгоритмі көмегімен кері шамаларды есептеу
Егер Эйлер φ(n) функциясы белгiлi болмаса, кеңейтiлген Евклид алгоритмiн қолдануға болады.
Евклид алгоритмнің алгебрада, тіпті жалпы математикада атқаратын ролі өте үлкен. Оң бүтін r 0 >r 1 >0 сандары берілсін. Олардың ең үлкен ортақ бөлгішін (ЕҮОБ) табу үшін төмендегі қалдықпен бөлу тізбегін іске асырамыз:
r0 = q 1 r 1 + r 2 , 0<r 2 <r 1
r1 = q 2 r 2 + r 3 , 0<r 3 <r 2
.
.
.
r m-2 = q m-1 r m-1 + r m , 0<r m <r m-1
r m-1 = q m r m .
Енді негізгі нәтижені дәлелдеу қиын емес:
ЕҮОБ(r 0 , r 1 ) = ЕҮОБ(r 1 , r 2 ) = … = ЕҮОБ(r m-1 , r m ) = r m
яғни, Евклид алгоритмін орындау нәтижесінде берілген сандардың ең үлкен ортақ бөлгішін табамыз:
ЕҮОБ(r 0 , r 1 ) = r m
Енді бұл алгоритмді былай кеңейтейік. Рекурренттік әдіспен төмендегідей t 0 , t 1 , …, t m сандар тізбегін анықтаймыз:
t 0 = 0,
t 1 = 1, және j≥2 үшін t j = t j-2 - q j-1 t j-1 деп ұйғарамыз.
Бұл тізбектің пайдасын келесі леммадан көреміз. Алдымен бір белгілеу енгізейік: егер а, b сандары n-ге бөлгенде бірдей қалдық берсе, онда а, b сандары n модулі бойынша тең дейміз және бұл қатынасты а ≡ b (mod n) деп жазып көрсетеміз.
Лемма 1 Жоғарыда іске асырылған кеңейтілген Евклид алгоритмінде пайда болатын сандар әрбір 0≤j≤m үшін r i ≡ t j r 1 (mod r 0 ) қатынасын қанағаттандырады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz