Үшінші, төртінші және жоғары дәрежелі алгебралық теңдеулерді шешу әдістері


МАЗМҰНЫ
КІРІСПЕ 3
1 ҮШІНШІ ЖӘНЕ ТӨРТІНШІ ДӘРЕЖЕЛІ ТЕҢДЕУЛЕРДІ
ШЕШУ ӘДІСТЕРІ 5
1. 1 Үшінші дәрежелі теңдеу 5
1. 2 Төртінші дәрежелі теңдеу 7
1. 3 Төртінші дәрежелі симметриялы теңдеу 8
1. 4 Коэффициенттеріне берілген қосымша шарттары бар төртінші дәрежелі
теңдеу 10
1. 5 Төртінші дәрежелі теңдеудің графиктік шешу әдісі 11
Есептер 15
2 ЖОҒАРЫ ДӘРЕЖЕЛІ ТЕҢДЕУЛЕР 20
2. 1 Қайтымды және симметриялы теңдеулердің дәрежесін төмендету 20
2. 2 Алгебралық теңдеулерді шешудің жасанды әдістері 24
2. 3 Нақты ось аралығында теңдеулерді зерттеу 27
Есептер 27
ҚОРЫТЫНДЫ 31
ӘДЕБИЕТТЕР ТІЗІМІ 32
КІРІСПЕ
Квадраттық теңдеулерді шешу әдістерін ежелгі гректер, үнділер алғаш рет пайдаланған. Ал үшінші дәрежелі теңдеулерді шешу әдістерін ең алғаш итальян ғалымдары Тартальей мен Кардано тапқан. Куб дәрежелі теңдеулерді шешу әдістері табылғаннан кейін, көп ұзамай Кардано оқушысы Феррари төртінші дәрежелі теңдеудің шешу әдісін тапты. Радикалда үшінші және төртінші дәрежелі теңдеулердің шешу әдістері табылғаннан кейін, енді бесінші дәрежелі теңдеуді шешу әдісін іздеуге ұмтылыстар жасалды. Бұл мақсатқа жету үшін көптеген күш жұмсалды.
1798 ж. итальян ғалымы Руффини төртінші дәрежеден жоғары теңдеулер радикалда шешілмейді деген шешім айтты, бірақта бұл пайымдау толық болмай шықты. Төртінші дәрежеден жоғары дәрежелі теңдеулерді радикалда шешу әдістері болмайтындығы туралы қатаң дәлелдемені Норвегия математигі Абель пайымдады. Сонда да, Руффинида, Абельде қойылған сұраққа толығымен, анық жауап бере алмады.
Данышпан, француз математигі Эврис Галуа (1811-1832) бұл сұраққа нақты жауап тапты. Галуаның басты еңбегі Ж. Лагранж бен Н. Абель бастаған алгебралық теңдеулердің радикал арқылы шешілетіндігі туралы зерттеулердің негізінде жасалған. Осының нәтижесінде Галуа теориясы шыққан.
ГАЛУА ТЕОРИЯСЫ - бір белгісізі бар жоғары дәрежелі алгебралық теңдеулер теориясы. Оның негізін Галуа салған. Галуа теориясында
x n +a 1 x n-1 +a 2 x n-2 +…++a n-1 x+a n =0; (1) түріндегі теңдеулерді шешу тәсілдері зерттеледі. Галуа зерттеулері алгебраның одан әрі дамуына шешуші ықпал жасады. Оның теориясы өзі қайтыс болғаннан кейін 14 жыл өткеннен соң жарыққа шықты. Галуа теориясын оның замандас ғалымдары да (О. Л. Коши мен А. Пуанкаре де) түсіне алмады. Галуа теориясын француз математигі Ж. Лиувилль жарыққа шығарды. (1) теңдеуінің белгігі бір жағдайдағы шешімділігінің қажетті және жеткілікті шарты былайша іске асырылады: әрбір теңдеуге оның түбірлерінен құрылған алмастырулар тобы сәйкес келеді. Бұл топ теңдеудің Галуа тобы деп аталады. Егер осы топ шешімді болса, онда оған сәйкес топтың шешімділігін тексеру керек. Ал топтың шешімділігі сол топтан жасалған композициялық қатардың индексіне қарап анықталады. Индекстер тізбегі тек жай сандардан тұрса, онда топ шешімді және керсінше болады. Дәрежесі 5-ке тең не одан жоғары (1) түріндегі алгебралық теңдеулердің, жалпы жағдайда, радикал арқылы шешілмейтіндігін Галуа (Абельге байланыссыз) өз бетінше дәлелдеді.
Көптеген жоғары дәрежелі теңдеулерді шешу үшін толық квадрат бөліп шығару, топтау, анықталған коэффиценттер әдісі, параметр енгізу әдістері, белгісіздерді белгілеу әдістері тағы да толып жатқан жасанды әдістер пайдаланылады. Осы әдістердің біршамасын алдағы тақырыптарда, теңдеулерді шешуде пайдаландым.
1 ҮШІНШІ ЖӘНЕ ТӨРТІНШІ ДӘРЕЖЕЛІ ТЕҢДЕУЛЕРДІ ШЕШУ ӘДІСТЕРІ
- Үшінші дәрежелі теңдеу.
Кез келген сандар өрісіндегі үшінші дәрежелі
х 3 +ах 2 +вх+с=0 (1. 1. 1)
теңдеуі берілсін.
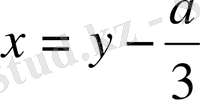 белгілеуін қолданып, (1. 1. 1) теңдеуді
белгілеуін қолданып, (1. 1. 1) теңдеуді
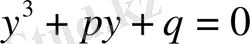 (1. 1. 2) түрге келтіреміз. Мұндағы
(1. 1. 2) түрге келтіреміз. Мұндағы
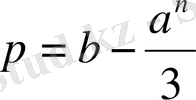 ,
,
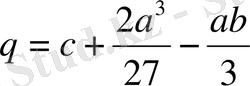 . Енді
. Енді
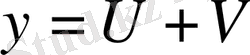 белгілеуінің екі жағын да кубтайық:
белгілеуінің екі жағын да кубтайық:
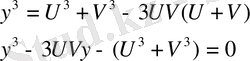
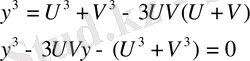 (1. 1. 3)
(1. 1. 3)
(1. 1. 2) мен (1. 1. 3) теңдеулерін салыстырып,
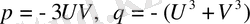 немесе
немесе
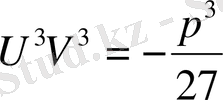 ,
,
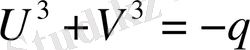 аламыз. Бұдан
аламыз. Бұдан
 пен
пен
 сандары
сандары
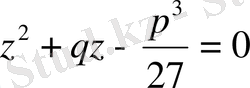 (1. 1. 4) квадрат тендеуге түбір болатындығы шығады. (1. 1. 4) теңдеуін шешсек
(1. 1. 4) квадрат тендеуге түбір болатындығы шығады. (1. 1. 4) теңдеуін шешсек
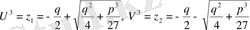
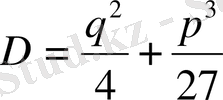
Сондықтан
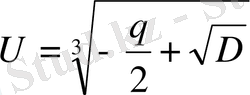 ,
,
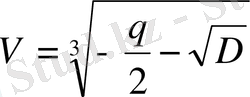
Сонымен, (1. 1. 2) куб теңдеуінің түбірлерін коэффициенттері арқылы өрнектейтін Кардан формуласы деп аталатын мына формуланы таптық:
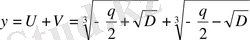
(1. 1. 2) теңдеуінің үш түбірі
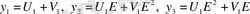 мұндағы Е-үш дәрежелі түбір астындағы бірдің алғашқы түбірі,
мұндағы Е-үш дәрежелі түбір астындағы бірдің алғашқы түбірі,
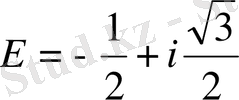 -деп алуға болады. (1. 1. 1) теңдеуінің үш түбірі
-деп алуға болады. (1. 1. 1) теңдеуінің үш түбірі
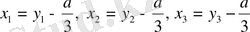 болады.
болады.
Теорема.
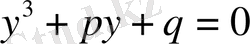 коэффициенттері нақты сан болатын теңдеу болсын және
коэффициенттері нақты сан болатын теңдеу болсын және
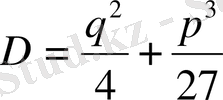 болсын. Онда:
болсын. Онда:
1) Егер
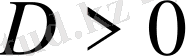 болса, онда теңдеудің бір нақты және екеуі түйіндес комплекс түбірлері болады.
болса, онда теңдеудің бір нақты және екеуі түйіндес комплекс түбірлері болады.
2) Егер
 болса, онда теңдеудің үш түбірі де нақты сандар және олардың екеуі өзара тең.
болса, онда теңдеудің үш түбірі де нақты сандар және олардың екеуі өзара тең.
3)
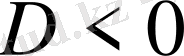 болса, онда теңдеудің барлық түбірлері әртүрлі нақты сандар болады.
болса, онда теңдеудің барлық түбірлері әртүрлі нақты сандар болады.
Мысал. Үшінші дәрежелі х 3 -3х+2=0 (*) тендеуін шешіңіз.
Шешуі. Бұл есепті екі тәсілмен шешуге болады.
1-тәсіл. Мұнда
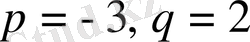 Онда
Онда
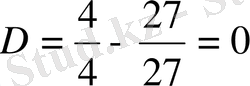
Сондықтан (*) теңдеуінің үш түбірі де нақты сандар және олардың екеуі өзара тең.
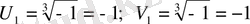
бұдан
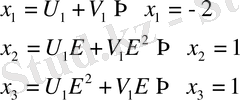
Демек, х=-2, х=1 сандары берілген теңдеудің шешуі немесе х=-2 шешуін тапқаннан кейін, қалған шешулерін табу үшін х 3 -3х+2 көпмүшелігін (х+2) -ге бөліп, шыққан бөліндінің (квадрат үшмүшеліктің) түбірлерін табу жеткілікті.
2-тәсіл. Көбейткішке жіктеу арқылы шешеміз.
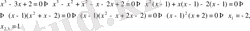
Демек, (*) теңдеуінің 3 түбірі болады.
1. 2 Төртінші дәрежелі теңдеу.
Кез келген сандар өрісіндегі х
4
+ах
3
+вх
2
+сх+d=0 (1. 2. 1) төртінші дәрежелі теңдеу берілсін. Бұл теңдеуді шешу үшін Ферари әдісін пайдаланып, куб теңдеуді шешуге келтіреміз. Берілген теңдеуді х
4
+ах
3
=-вх
2
-сх-d түрінде жазып аламыз. Осы теңдеудің екі жағына да
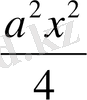 өрнегін қосамыз, сонда теңдеудің сол жағы екі санның қосындысының толық квадратын береді:
өрнегін қосамыз, сонда теңдеудің сол жағы екі санның қосындысының толық квадратын береді:
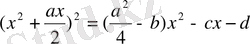
Сонғы теңдеудің екі жағына да
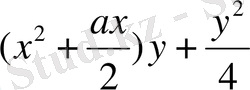 -өрнегін қоссақ, теңдеудің сол жағы үш санның қосындысының толық квадратын береді:
-өрнегін қоссақ, теңдеудің сол жағы үш санның қосындысының толық квадратын береді:
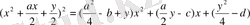
Енді у-ті (1. 2. 2) теңдеуінің оң жағы толық квадрат болатындай етіп таңдаймыз. Ол үшін
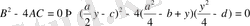 болу керек. Бұл үшінші дәрежелі теңдеу. Оның бір түбірі у
0
-ді тапсақ жеткілікті. y
0
-ді (1. 2. 2) теңдеуіндегі орнына қойып,
болу керек. Бұл үшінші дәрежелі теңдеу. Оның бір түбірі у
0
-ді тапсақ жеткілікті. y
0
-ді (1. 2. 2) теңдеуіндегі орнына қойып,
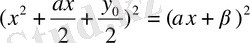 Equation. 3
Equation. 3
теңдеуін аламыз. Соңғы теңдеу мынадай:
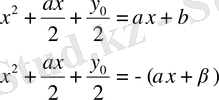
екі теңдеуге мәндес. Бұл теңдеулерді шешіп, берілген теңдеудің төрт түбірін аламыз.
Мысал. Төртінші дәрежелі теңдеуді шешіңіз
х 4 -2х 3 +2х 2 +4х-8=0
Шешуі: Алдымен х
4
-2х
3
=-2х
2
-4х+8 түрінде жазып алып, теңдеудің екі жағына да
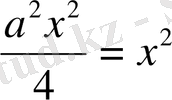 өрнегін қосамыз,
өрнегін қосамыз,
(х 2 -х) 2 =-х 2 -4х+8
Осы теңдеудің екі жағына да
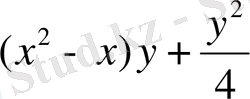 өрнегін қоссақ,
өрнегін қоссақ,
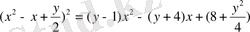
теңдеуін аламыз. y-ті соңғы теңдеудің оң жағы толық квадрат болатындай етіп таңдаймыз. Ол үшін
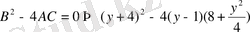
болу керек, мұнда
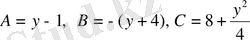
Бұл у 3 -2у 2 +24у-48=0 үшінші дәрежелі теңдеу. Оның бір түбірі
у
2
(у-2) +24(у-2) =0
 (у-2) (у
2
+24) =0; у
0
=2 болады.
(у-2) (у
2
+24) =0; у
0
=2 болады.
Ендеше (х
2
-х+1)
2
=х
2
-6х+9
 (х
2
-х+1)
2
=(х-3)
2
(х
2
-х+1)
2
=(х-3)
2
бұдан
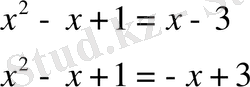 теңдеулерін алдық. Теңдеулерді шешіп, берілген төртінші дәрежелі теңдеудің төрт түбірін аламыз:
теңдеулерін алдық. Теңдеулерді шешіп, берілген төртінші дәрежелі теңдеудің төрт түбірін аламыз:
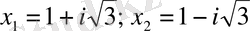 ;
;
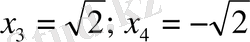
- Төртінші дәрежелі симметриялы теңдеулер.
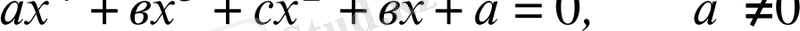 , (1. 3. 1)
, (1. 3. 1)
түріндегі теңдеу төртінші дәрежелі симметриялы теңдеу деп аталады.
х=0
(1. 3. 1) теңдеуінің түбірі болмағандықтан, теңдеудің екі жағында
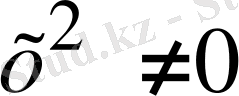 бөлсек, келесі түрдегі теңдеуді аламыз:
бөлсек, келесі түрдегі теңдеуді аламыз:
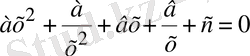 (1. 3. 2)
(1. 3. 2)
(1. 3. 2) теңдеуін төмендегідей жазып алайық:
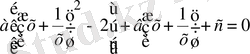 .
.
Бұл теңдеуді шешу үшін
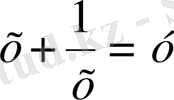 белгілеуін енгіземіз, онда
белгілеуін енгіземіз, онда
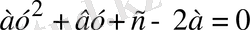 (1. 3. 3)
(1. 3. 3)
Егер соңғы теңдеудің у 1 және у 2 екі түбірі болса, онда бастапқы теңдеу мынадай болады
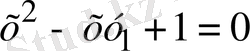 және
және
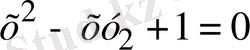
Егер (1. 3. 3) теңдеуінің
у
0
бір түбірі болса, онда бастапқы теңдеу болмаса онда бастапқы
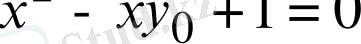 теңдеуіне тең.
теңдеуіне тең.
Ал, егер (1. 3. 3) теңдеуінің түбірі болмаса, онда бастапқы берілген теңдеудің де түбірі болмайды.
Мысал. Теңдеуді шешіңіз
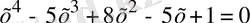 (1. 3. 4)
(1. 3. 4)
Шешуі: Берілген теңдеу төртінші дәрежелі симметриялы теңдеу.
х=0
теңдеудің түбірі болмағандықтан (1. 3. 4) -ң екі жағында
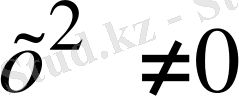 бөліп, берілген теңдеуге тепе-тең теңдеуді аламыз:
бөліп, берілген теңдеуге тепе-тең теңдеуді аламыз:
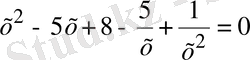 (1. 3. 5)
(1. 3. 5)
Топтастырсақ (1. 3. 5) теңдеуі мына түрге келеді:
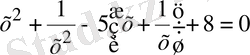
немесе
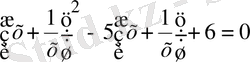
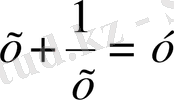 деп алып,
деп алып,
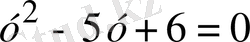
 және
және
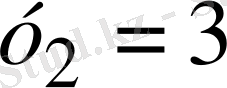 екі түбірі болатын теңдеуін аламыз. Ендеше, түбірлерді белгілеудің орнына қойсақ
екі түбірі болатын теңдеуін аламыз. Ендеше, түбірлерді белгілеудің орнына қойсақ
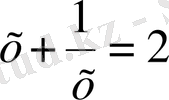 және
және
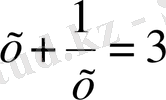
болады. Бірінші теңдікті шешсек
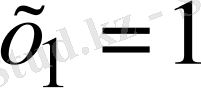 , ал екінші теңдіктің шешімі
, ал екінші теңдіктің шешімі
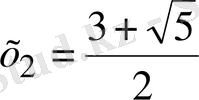 және
және
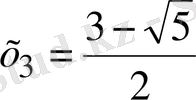 болатынын көреміз. Сонымен берілген (1. 3. 4) теңдеуінің үш түбірі бар.
болатынын көреміз. Сонымен берілген (1. 3. 4) теңдеуінің үш түбірі бар.
Жауабы:
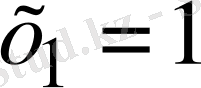 ,
,
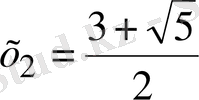 ,
,
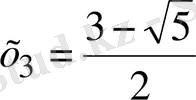 .
.
1. 4 Коэффицентіне берілген қосымша шарттары бар төртінші дәрежелі
теңдеу
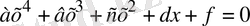 (1. 4. 1)
(1. 4. 1)
төртінші дәрежелі теңдеуін қарастырайық, мұндағы а≠0, в≠0, d≠0 және
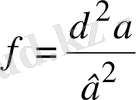 . х=0 теңдеудің түбірі болмағандықтан, оны х
2
≠0-ге бөліп,
. х=0 теңдеудің түбірі болмағандықтан, оны х
2
≠0-ге бөліп,
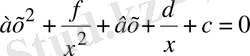 түріндегі теңдеуді аламыз.
түріндегі теңдеуді аламыз.
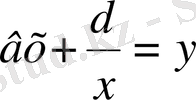 деп алып және
деп алып және
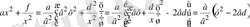
екенін ескеріп, (1. 4. 1) теңдеуін келесі түрде жазамыз
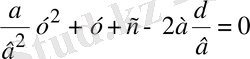 .
.
Бұл квадраттық теңдеудің шешімін таба отырып, одан кейін біз бастапқы берілген теңдеудің түбірін аламыз.
Мысал. Теңдеуді шешіңіз
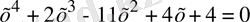 (1. 4. 2)
(1. 4. 2)
Шешуі: Берілген теңдеуде а=1, в=2, d=4, f=4. a≠0, в≠0, d≠0,
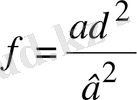 . х=0 (1. 4. 2) теңдеуінің түбірі болмайды, сондықтан теңдеудің екі жағында х
2
≠0-ге бөліп, мүшелерін топтастырамыз
. х=0 (1. 4. 2) теңдеуінің түбірі болмайды, сондықтан теңдеудің екі жағында х
2
≠0-ге бөліп, мүшелерін топтастырамыз
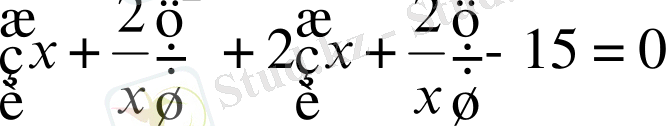
түріндегі теңдеуді аламыз.
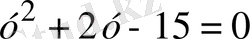 теңдеуінің
у
1
=-5 және
у
2
=3 түбірлері бар. Ендеше, бастапқы берілген (1. 4. 2) теңдеуінің түбірлерін
теңдеуінің
у
1
=-5 және
у
2
=3 түбірлері бар. Ендеше, бастапқы берілген (1. 4. 2) теңдеуінің түбірлерін
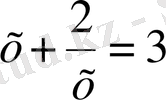 және
және
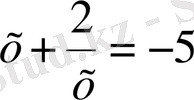 теңдіктерін шешу арқылы табамыз, яғни
х
1
=2,
х
2
=1,
теңдіктерін шешу арқылы табамыз, яғни
х
1
=2,
х
2
=1,
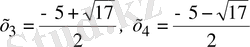 .
.
Жауабы:
х
1
=2,
х
2
=1,
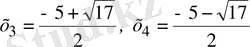 .
.
1. 5 Төртінші дәрежелі теңдеудің графиктік шешу әдісі
Төртінші дәрежелі теңдеу мына түрде болады:
а 0 z 4 +a 1 z 3 +a 2 z 2 +a 3 z +a 4 =0, а 0 ≠0 (1. 5. 1)
Ең бірінші бұл теңдеудің үшінші дәрежелі белгісіздің коэффициентін нөлге, ал ең үлкен коэффициент бірге тең болатындай етіп түрлендіреміз. Бұл үшін жаңа белгісіз енгіземіз z=x+t. Теңдеу мынадай түрге келеді:
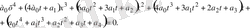
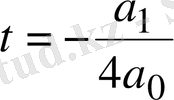 деп алсақ, онда теңдеу келесі түрге келеді
деп алсақ, онда теңдеу келесі түрге келеді
а 0 х 4 +А 2 х 2 +А 3 х+А 4 =0, (1. 5. 2)
мұндағы
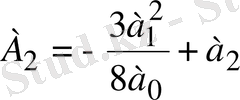 ;
;
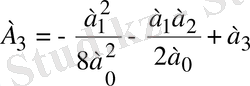 ;
;
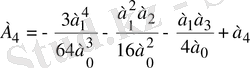 .
.
(1. 5. 2) теңдеуінің екі жағында а 0 -ге бөлейік
х 4 +nx 2 +px+q=0 (1. 5. 3)
мұндағы
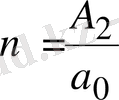 Equation. 3,
Equation. 3,
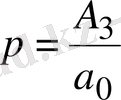 Equation. 3,
Equation. 3,
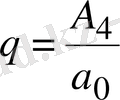 Equation. 3 (1. 5. 3) теңдеуін жүйелі түрде былай өзгертеміз:
Equation. 3 (1. 5. 3) теңдеуін жүйелі түрде былай өзгертеміз:
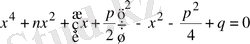 ;
;
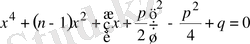 ;
;
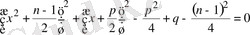 .
.
Екінші белгісіз енгіземіз у=х 2 , онда (1. 5. 3) теңдеуін келесі теңдеулер жүйесімен ауыстыруға болады.
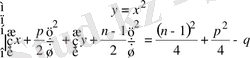 (1. 5. 4)
(1. 5. 4)
(1. 5. 4) жүйесінің бірінші теңдеуі парабола теңдеуі, екіншісі центрі
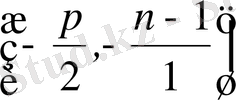 нүктесінде, ал радиусы
нүктесінде, ал радиусы
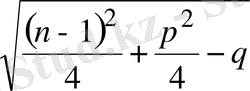 болатын шеңбердің теңдеуі.
болатын шеңбердің теңдеуі.
(1. 5. 4) теңдеуінің шешімі болып парабола мен шеңбердің қиылысу нүктесінің абсцисасы табылады. Парабола барлық (1. 5. 3) теңдеуі үшін жалғыз және сол болады, ал шеңбер төртінші дәрежелі бір теңдеуден келесі теңдеуге өткенде ауысады.
Мысал 1) Теңдеудің графикалық нақты түбірлерін табыңыз
х 4 -7х 2 +6х=0.
Шешуі: Теңдеуді келесі түрде өзгертеміз
х 4 -7х 2 +(х+3) 2 -х 2 -9=0;
х 4 -8х 2 +(х+3) 2 -9=0;
(х 2 -4) +(х+3) 2 -25=0.
Екінші у=х 2 белгісізін енгізіп, теңдеулер жүйесін аламыз.
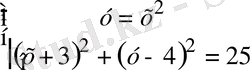
Парабола мен шеңбердің қиылысу нүктелері (-3, 9) ; (0, 0) ; (1, 1) ; (2, 4) . Теңдеудің түбірлері х 1 =-3; х 2 =0; х 3 =1; х 4 =2
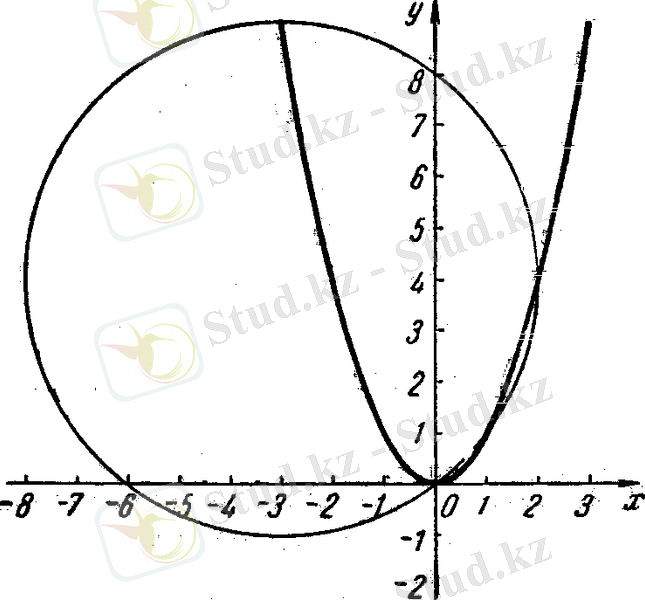
1 - сурет.
Жауабы: х 1 =-3; х 2 =0; х 3 =1; х 4 =2.
Мысал 2) Теңдеудің графикалық нақты түбірлерін табыңыз.
z 4 +4z 3 +3z 2 +8z+1=0.
Шешуі. Теңдеудің үшінші дәрежелі белгісізінің коэффициенті нөлге тең болу үшін z=х-1 жаңа белгісізін енгіземіз. Сонда теңдеу мына түрге келеді:
х 4 -3х 2 -6х+9=0.
Теңдеуді түрлендірейік:
х 4 -4х 2 +(х-3) 2 =0
(х 2 -2) 2 +(х-3) 2 =4.
у=х 2 екінші белгісізін енгіземіз. Теңдеулер жүйесін аламыз
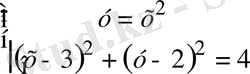
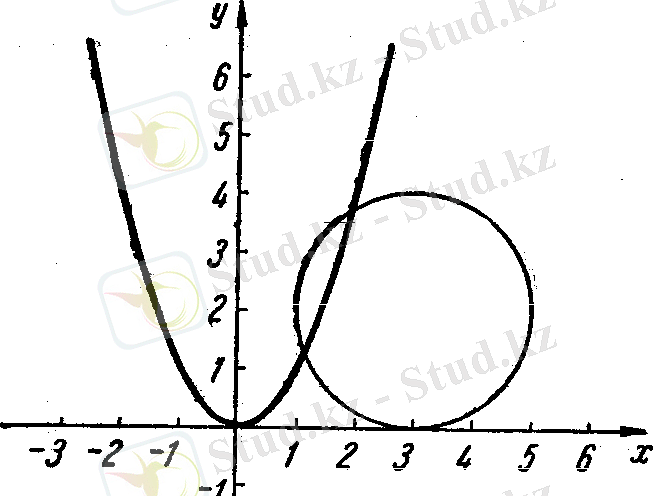
2 - сурет.
графиктен көрініп тұрғандай парабола мен шеңбер (1, 1; 1, 2) және (1, 9; 3, 6) нүктелерінде қиылысып тұр. Ендеше теңдеудің екі нақты түбірі бар. Нақты түбірлерді жуық шамамен аламыз, яғни х 1 ≈1, 1; х 2 ≈1, 9. Осыдан z 1 және z 2 табатын болсақ z 1 ≈0, 1; z 2 ≈0, 9.
Жауабы: z 1 ≈0, 1; z 2 ≈0, 9.
Мысал 3) Теңдеудің графикалық нақты түбірлерін табыңыз
z 4 -8z 3 +31z 2 +60z+49=0.
Шешуі: Жаңа белгісізді енгіземіз z=x+2
х 4 +7х 2 +5=0
теңдеуін аламыз. Бұл теңдеуді былай етіп түрлендіреміз:
х 4 +6х 2 +х 2 +5=0
(х 2 +3) 2 +х 2 -4=0.
Екінші у=х 2 белгісізін енгізіп, теңдеулер жүйесін аламыз
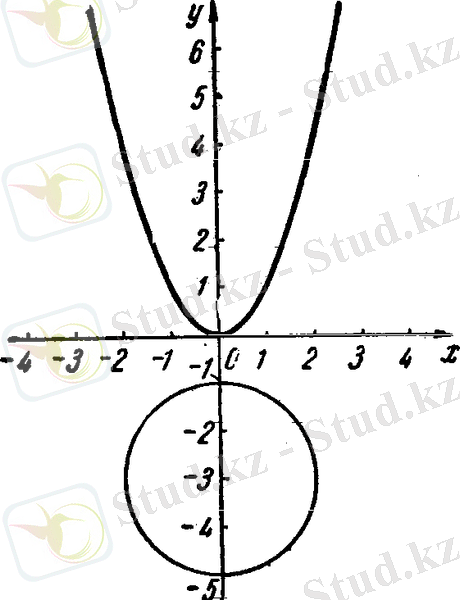
3- сурет.
Парабола мен шеңбер қиылыспайды. Яғни берілген төртінші дәрежелі теңдеудің нақты түбірлері жоқ.
Жауабы: теңдеудің нақты түбірлері жоқ.
Есептер
1) Теңдеуді шешіңіз
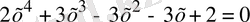 . (1)
. (1)
Шешуі: Берілген теңдеу төртінші дәрежелі қайтымды теңдеу болып табылады (λ=-1) . х=0 теңдеудің түбірі болмағандықтан, берілген теңдеу келесі теңдеумен тепе-тең
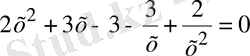 .
.
Соңғы теңдеуді мына түрде жазамыз
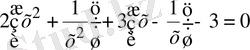
немесе
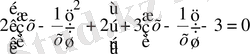 (2)
(2)
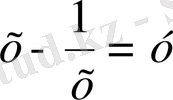 белгілеуін енгізсек, (2) теңдеуі
белгілеуін енгізсек, (2) теңдеуі
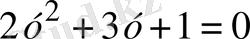 түріне келеді. Бұл теңдеудің у
1
=-1 және
түріне келеді. Бұл теңдеудің у
1
=-1 және
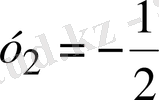 түбірі табылады.
түбірі табылады.
Олай болса
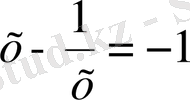 және
және
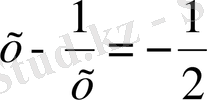 .
.
Бірінші теңдіктің шешімдері
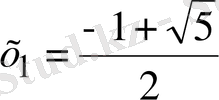 және
және
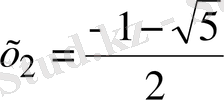 , ал екінші теңдеудің
, ал екінші теңдеудің
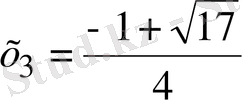 және
және
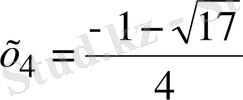 шешімі болады. Бұл төрт шешім берілген теңдеудің түбірлері болып табылады.
шешімі болады. Бұл төрт шешім берілген теңдеудің түбірлері болып табылады.
Жауабы:
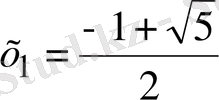 ,
,
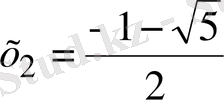 ,
,
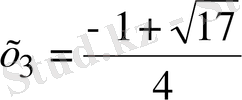 ,
,
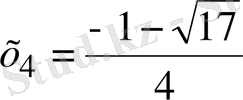 .
.
2) Теңдеуді шешіңіз
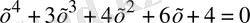 . (3)
. (3)
Шешуі: а≠0, в≠0, с≠0, d≠0 және
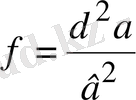 болғандықтан коэффицентіне берілген қосымша шартты пайдаланамыз. Ендеше алдымен берілген теңдеуді х
2
≠0-ге бөліп, мүшелерін топтастырамыз
болғандықтан коэффицентіне берілген қосымша шартты пайдаланамыз. Ендеше алдымен берілген теңдеуді х
2
≠0-ге бөліп, мүшелерін топтастырамыз
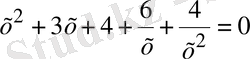 (4)
(4)
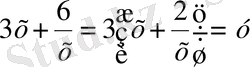
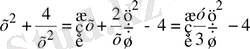
Ендеше (4) теңдеуі мынадай квадраттық теңдеуге келеді
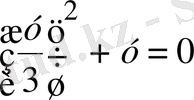
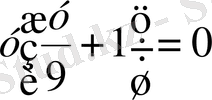
у 1 =0 және у 2 =-9
Табылған түбірлерді белгілеудің орнына қойсақ төмендегідей теңдіктер шығады:
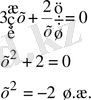
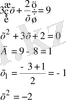
Сонымен берілген (3) теңдеуінің екі түбірі бар
Жауабы: х 1 =-1, х 2 =-2.
3) Теңдеуді шешіңіз
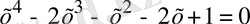
Шешуі: Берілген теңдеу төртінші дәрежелі симметриялы теңдеу. х=0 теңдеудің түбірі болмағандықтан теңдеуді х 2 ≠0-ге бөліп, мүшелерін топтастырып
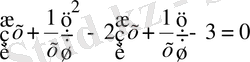
теңдеуін аламыз.
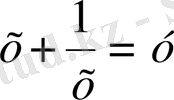 белгілеуін енгізсек,
белгілеуін енгізсек,
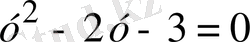 квадраттық теңдеуі шығады. Бұл квадраттық теңдеудің у
1
=3, у
2
=-1 түбірлері болады.
квадраттық теңдеуі шығады. Бұл квадраттық теңдеудің у
1
=3, у
2
=-1 түбірлері болады.
Олай болса,
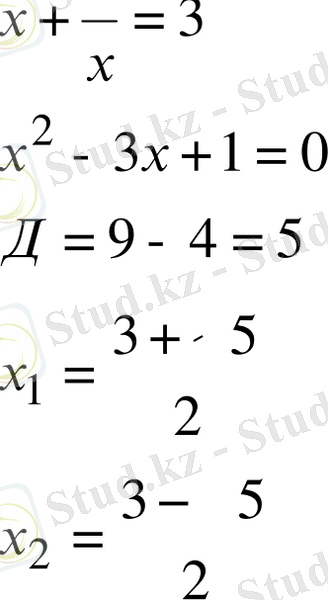
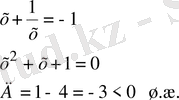
Ендеше берілген теңдеудің екі түбірі бар.
Жауабы:
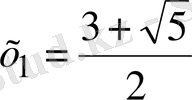 ,
,
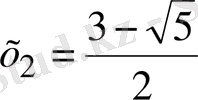 .
.
4) Теңдеуді шешіңіз.
2(a-x) 4 -9(a-x) 3 (x-b) +14(a-x) 2 (x-b) 2 -9(a-x) (x-b) 3 +2(x-b) 4 =0
Шешуі: Берілген төртінші дәрежелі теңдеуді шешу үшін a-x=y(x-b) белгілеуін енгіземіз.
2y 4 (x-b) 4 -9y 3 (x-b) 4 +14y 2 (x-b) 4 -9y(x-b) 4 +2(x-b) 4 =0
(x-b) 4 [2y 4 -9y 3 +14y 2 -9y+2] =0
(x-b) 4 =0
2y 4 -9y 3 +14y 2 -9y+2=0
Соңғы теңдеудің екі жағында y 2 ≠0 бөлсек
2y
2
-9y+14-
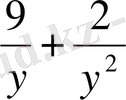 =0 теңдеуін аламыз.
=0 теңдеуін аламыз.
2(y
2
+
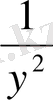 ) -9(y+
) -9(y+
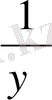 ) +14=0
) +14=0
y+
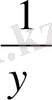 =z
=z
2z 2 -9z+10=0
z
1
=2, z
2
=

y+
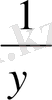 =2 және y+
=2 және y+
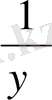 =
=

y
2
-2y+1=0 y
2
-
 y+1=0
y+1=0
y
1
=y
2
=1 y
3
=
 , y
4
=2
, y
4
=2
a-x=x-b a-x=
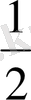 (x-b) a-x=2(x-b)
(x-b) a-x=2(x-b)
x
1
=x
2
=
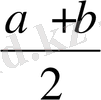 Equation. 3 x
3
=
Equation. 3 x
3
=
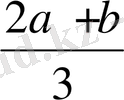 Equation. 3 x
4
=
Equation. 3 x
4
=
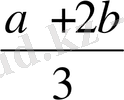 Equation. 3
Equation. 3
Жауабы: егер a≠b, онда x
1
=x
2
=
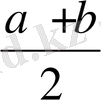 , x
3
=
, x
3
=
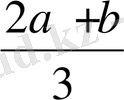 , x
4
=
, x
4
=
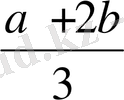 егер a=b, онда x=a
егер a=b, онда x=a
5) Графиктік тәсілмен шешіңіз
z 4 -4z 3 +3z 2 +2z-1=0
Шешуі: Берілген төртінші дәрежелі теңдеуді графиктік тәсілмен шешу үшін үш дәрежелі белгісіздің коэффициентін нөлге айналдыруымыз қажет, ол үшін z=x+1 белгілеуін енгіземіз.
(x+1) 4 -4(x+1) 3 +3(x+1) 2 +2(x+1) -1=0
x 4 +4x 2 +1+4x 3 +2x 2 +4x-4x 3 -12x 2 -12x-4+3x 2 +6x+3+2x+1=0
x 4 -3x 2 +1=0
x 4 -4x 2 +x 2 +1=0
(x 2 -2) 2 +x 2 =3
y=x 2
x
2
+(y-2)
2
=3
 Equation. 3
Equation. 3
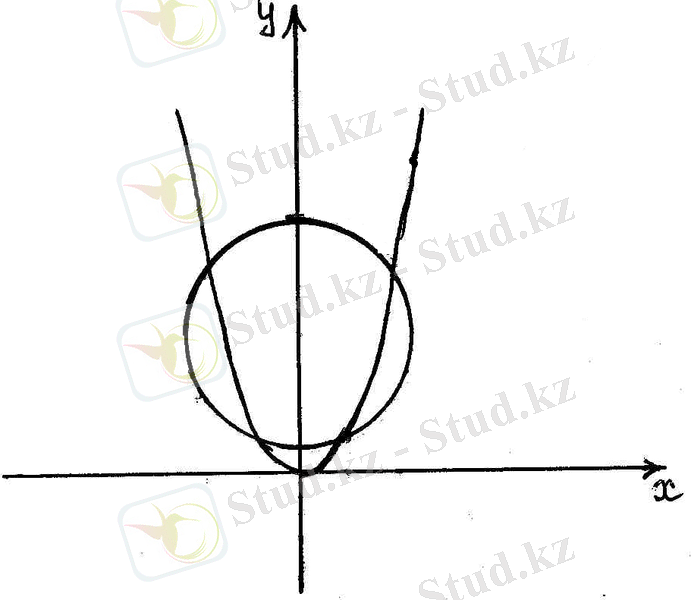
4 - сурет.
Парабола мен шеңбердің қиылысу нүктелері (0, 7; 0, 3), (1, 5; 2, 6), (-0, 7; 0, 3),
(-1, 5; 2, 6), ендеше x 1 ≈0, 7; x 2 ≈1, 5; x 3 ≈-0, 7; x 4 ≈-1, 5.
Жауабы: z 1 ≈1, 7; z 2 ≈2, 5; z 3 ≈0, 3; z 4 ≈-0, 5.
2 ЖОҒАРЫ ДӘРЕЖЕЛІ ТЕҢДЕУЛЕР
2. 1 Қайтымды және симметриялы теңдеулердің дәрежесін төмендету
Анықтама. Теңдеу тақ дәрежелі қайтымды теңдеу деп аталады, егер
a 0 x 2n+1 +a 1 x 2n +…+a n x n+1 +λa n x n +λ 2 a n-1 x n-1 +…+a 0 λ 2n+1 =0, (2. 1. 1)
түрінде болса және жұп дәрежелі болады, егер
a 0 x 2n +a 1 x 2n-1 +…+a n-1 x n+1 +a n x n +λa n-1 x n-1 +λ 2 a n-2 x n-2 +…+a 0 λ n =0, (2. 1. 2)
(λ- кез-келген сан)
Мысалы: 2x 5 +3x 4 -2x 3 -6x 2 +81x+486=0 теңдеуі қайтымды, мұндағы λ=3
Теорема 1. Жұп дәрежелі қайтымды теңдеудің x=-λ түбірі болады.
Дәлелдеуі. (2. 1. 1) қайтымды теңдеуін қарастырайық. Оны мына түрде жазуға болады:
a 0 (x 2n+1 +λ 2n+1 ) + a 0 x(x 2n-1 +λ 2n-1 ) +…+ a n x n (x+λ) =0.
x=-λ болғанда соңғы теңдеудің әрбір қосылмасы нөлге айналады.
Теорема 2. Тақ дәрежелі қайтымды теңдеудің оң және сол жағында (x+λ) -ға бөлгенде жұп дәрежелі қайтымды теңдеу пайда болады.
Дәлелдеуі. (2. 1. 1) теңдеуінің сол жағын (x+λ) -ға бөліп, дербесті белгілейміз: b 0 x 2n +b 1 x 2n-1 +…+b 2n . Тепе-теңдік аламыз
a 0 x 2n+1 +a 1 x 2n +…+a k x 2n-k+1 +…+a n x n+1 +λa n x n +λ 3 a n-1 x n-1 +…+λ 2n-2k+1 a k x k +…+a 0 λ 2n+1 ≡
≡(x+λ) ( b 0 x 2n +b 1 x 2n-1 +…+b k x 2n-k +…+b 2n ) . (2. 1. 3)
Біз
b 2n =λ 2n b 0 ; b 2n-1 =λ 2n-2 b 1 ; b 2n-2 =λ 2n-4 b 2 ; …; b n+1 =λ 2 b n-1
болатынын дәлелдейміз.
Дәлелдеу үшін математикалық индукция әдісін қолданамыз. (2. 1. 3) тепе-теңдіктің оң жақ және сол жағындағы х 2n+1 -ң коэффициенттерін салыстырсақ
a 0 =b 0 , (2. 1. 4)
(2. 1. 3) тепе-теңдігінің бос мүшелерін салыстырсақ
a 0 λ 2n+1 =λb 2n (2. 1. 5)
теңдігн аламыз. (2. 1. 4) және (2. 1. 5) теңдіктерінен мына теңдік шығады:
b 2n =λ 2n b 0 .
b 2n =λ 2n b 0 ; b 2n-1 =λ 2n-2 b 1 ; b 2n-2 =λ 2n-4 b 2 ; …; b 2n-k =λ 2n-2k b k ,
деп ұйғарайық, мұндағы 0≤k<n. Сонда
b 2n-k-1 =λ 2n-2k-2 b k+1
теңдігін дәлелдейміз. (2. 1. 3) тепе-теңдігінің оң және сол жағындағы x k+1 коэффициенттерін салыстырайық :
λ
2n-2k-1
a
k+1
=λb
2n-k-1
+b
2n-k
.
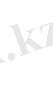 (2. 1. 6)
(2. 1. 6)
(2. 1. 3) тепе-теңдігінің оң және сол жағындағы x 2n-k коэффициенттерін салыстырайық :
a k+1 =λb k +b k+1 . (2. 1. 7)
(2. 1. 6) және (2. 1. 7) теңдіктерінен λ 2n-2k b k +λ 2n-2k-1 b k+1 =λb 2n-k-1 +b 2n-k аламыз. Бірақ b 2n-k =λ 2n-2k b k болғандықтан b 2n-k-1 =λ 2n-2k-2 b k+1 . Теорема 2-ден тақ дәрежелі қайтымды теңдеуді шешу жұп дәрежелі қайтымды теңдеуді шешумен сәйкес келеді келеді.
Мысал 1) Қайтымды теңдеуді қарастырайық
a 0 x 4 +a 1 x 3 +a 2 x 2 +λa 1 x+λ 2 a 0 =0.
Теңдеудің екі жағында x 2 ≠0-ге бөлейік. Онда
a
0
x
2
+a
1
x+a
2
+λa
1
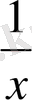 +λ
2
a
0
+λ
2
a
0
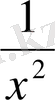 =0
=0
теңдеуін аламыз. Бірінші қосындыны соңғымен, екіншіні соңғының алдыңғы мүшесімен біріктірсек
a
0
(x
2
+
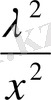 ) +a
1
(x+
) +a
1
(x+
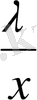 ) +a
2
=0 (2. 1. 8)
) +a
2
=0 (2. 1. 8)
болады. y=x+
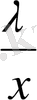 жаңа белгісіз енгіземіз. Сонда
жаңа белгісіз енгіземіз. Сонда
x
2
+2λ+
 =y
2
=y
2
осыдан
x
2
+
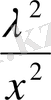 =y
2
-2λ.
=y
2
-2λ.
(2. 1. 8) теңдеуінің x+
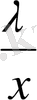 және x
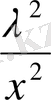
2
+
және x
2
+
 орнына y белгісізін енгізіп a
0
y
2
+ a
1
y+ (a
2
-2λa
0
) =0 теңдеуін аламыз. Бұл теңдеудің комплекс сандар обылысында y
1
және y
2
екі шешімі болады. х белгісізін x+
орнына y белгісізін енгізіп a
0
y
2
+ a
1
y+ (a
2
-2λa
0
) =0 теңдеуін аламыз. Бұл теңдеудің комплекс сандар обылысында y
1
және y
2
екі шешімі болады. х белгісізін x+
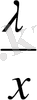 = y
1
және x+
= y
1
және x+
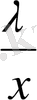 = y
2
теңдеуінен табамыз, яғни
= y
2
теңдеуінен табамыз, яғни
x 2 -xy 1 +λ=0 және x 2 -xy 2 +λ=0.
Сонымен, 4-ші дәрежелі қайтымды теңдеуді шешу үш квадраттық теңдеуді шешуге келді.
Мысал 2. Теңдеуді шешіңіз
x 5 -5x 4 +6x 3 +18x 2 -135x+243=0
Берілген теңдеу қайтымды λ=3, ендеше теорема 1 бойынша теңдеудің x 1 =-3 түбірі болады. Теңдеуді топтастырайық
(x 5 +243) -5x(x 3 +27) +6x 2 (x+3) =0
(x+3) (x 4 -3x 3 +9x 2 -27x+81) -5x(x+3) (x 2 -3x+9) +6x 2 (x+3) =0
(x+3) [x 4 -8x 3 +30x 2 -72x+81] =0
x+3=0
x 4 -8x 3 +30x 2 -72x+81=0
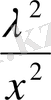
Соңғы теңдеудің екі жағында х 2 ≠0 бөліп, топтастырсақ төмендегідей түрдегі теңдеу аламыз:
x
2
-8x+30-
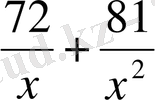 =0
=0
(x
2
+
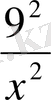 ) -8(x+
) -8(x+
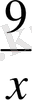 ) +30=0
) +30=0
x+
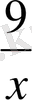 =y белгілеуін енгізсек y-тен тәуелді квадрат теңдеу аламыз
=y белгілеуін енгізсек y-тен тәуелді квадрат теңдеу аламыз
y 2 -8y+12=0
Соңғы теңдеуді шешіп, y 1 =6, y 2 =2 түбірлерін аламыз. Бұл түбірлерді белгілеу енгізген теңдеудің орнына қойып, бастапқы берілген теңдеудің түбірлерін табамыз.
x+
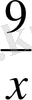 =6, x+
=6, x+
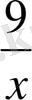 =2
=2
x
2
=x
3
=3, x
4
=1+2
 Equation. 3
Equation. 3
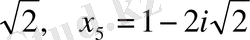 .
.
Жауабы: x
1
=-3, x
2
=x
3
=3, x
4
=1+2
 Equation. 3
Equation. 3
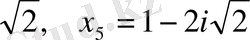 .
.
Анықтама. n-ші дәрежелі теңдеу симметриялы деп аталады, егер оның x k және x n-k коэффициенттері тең болса. Сондықтанда, симметриялы теңдеу мына түрде болады:
a 0 x n +a 1 x n-1 +…+a k x n-k +…+a k x k +…+a 1 x+a 0 =0.
Симетриялы теңдеу қайтымды теңдеудің дербес түбірі болып табылады (λ=1)
Мысалы. 2x 4 +3x 3 +5x 2 +3x+2=0 теңдеуі симметриялы.
Қайтымды теңдеуге қатысты теорема 1 және теорема 2 - ден келесі теоремалар шығады:
Теорема 3. Тақ дәрежелі симметриялы теңдеудің -1 түбірі болады.
Теорема 4. Тақ дәрежелі симметриялы теңдеуді x+1-ге бөлгенде жұп дәрежелі симметриялы теңдеу пайда болады.
Симметриялы теңдеулер қайтымды теңдеуді шешу әдістері сияқты шешіледі.
Мысал 3) Теңдеуді шешіңіз
x 4 -2x 3 -x 2 -2x+1=0.
Шешуі: Теңдеудің екі жағында х 2 ≠0 бөліп, топтастырсақ мынадай теңдеудің түбірін аламыз
(x
2
+
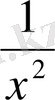 ) -2(x+
) -2(x+
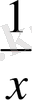 ) -1=0.
) -1=0.
x+
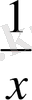 =y деп ұйғарайық. Онда y
2
-2y-3=0 түріне келеді. y
1
=3, y
2
=-1 соңғы теңдеудің түбірлері. Енді екі квадраттық теңдеуді шешеміз, яғни x+
=y деп ұйғарайық. Онда y
2
-2y-3=0 түріне келеді. y
1
=3, y
2
=-1 соңғы теңдеудің түбірлері. Енді екі квадраттық теңдеуді шешеміз, яғни x+
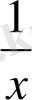 =3 және x+
=3 және x+
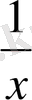 =-1
=-1
Жауабы: x
1
=

Мысал 4) Теңдеуді шешіңіз
x 7 -2x 6 +3x 5 -x 4 -x 3 +3x 2 -2x+1=0.
Шешуі: Тақ дәрежелі симметриялы теңдеу болғандықтан берілген теңдеудің х=-1 түбірі болады. Теңдеудің екі жағында x+1-ге бөлейік, онда жұп дәрежелі теңдеу аламыз
x 6 -3x 5 +6x 4 -7x 3 +6x 2 -3x+1=0.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz