«Пифагор теоремасын басқа тәсілмен дәлелдеу»

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

Е. А. Букетов атындағы Қарағанды мемлекеттік университеті

Қарағанды облысының білім департаменті

Орта оқу орындары оқушыларының аймақтық ғылыми - практикалық конференциясы

« Жоғары математика және мектеп »

Қарағанды, 24 сәуір 2010 жыл

«Пифагор теоремасын басқа тәсілмен дәлелдеу»

Айтжанова Б. З.

9Ә, №15 мектеп, Балқаш қаласы

Үсенбекова С. Ү.

Қарағанды - 2010

Мазмұны

Аннотация . . . 3-5

І. Кіріспе . . . 6-7

ІІ. Негізгі бөлім:

1. Пифагор теоремасы жайында . . . 9

2. Теореманы дәлелдеу тәсілдері . . . 10-16

а) Теореманы дәлелдеудің бірінші тәсілі

ә) Теореманы дәлелдеудің екінші тәсілі

б) Теореманы дәлелдеудің үшінші тәсілі

в) Теореманы дәлелдеудің төртінші тәсілі

г) Теореманы дәлелдеудің бесінші тәсілі

д) Теореманы дәлелдеудің алтыншы тәсілі

е) Теореманы дәлелдеудің жетінші тәсілі

3. Сипаттау . . . 17-24

ІІІ. Қорытынды . . . 25-26

ІҮ. Пайдаланған әдебиеттер тізімі . . . 27

Аннотация.

Тақырыбы. «Пифагор теоремасын басқа тәсілмен дәлелдеу»

Зерттеу мақсаты. Пифагор теоремасын әр түрлі жолдармен дәлелдеуге болатынын көрсету. Мектеп математика курсының мазмұнында қарастырылып отырған теорема не үшін керек екендігін оқушыларға барлық кездескен жағдайларда түсінікті болатындай етіп ашу. Оқушылардың логикалық ой - қабілеттерін арттыру.

Тақырыптың өзектілігі . Зерттеу жұмысында Пифагор теоремасын зерттеп, басқа жолдармен дәлелдеу. Пифагор теоремасы математика саласының дамуына қажет болғандықтан, бұл теореманы тереңірек ұғып, түсіну. Сонымен қоса оқушылардың математика пәніне қызығушылығын арттыру.

Гипотеза. Егер Пифагор теоремасын дәлелдеу процесінде және оқу-материалдарын игеру барысында зерттеу әдістерін жетілдіріп, деректерді тиімді әрі жүйелі пайдалансақ, онда оқушылардың зерттеу құзіреттілігі және коммуникативтік, ақпараттық құзіреттілігі өз мәнінде дамып, сонымен қоса оқушылардың математикаға деген қызығушылығы артады деген ойдамын.

Зерттеу кезеңдері. Мен өзімнің ғылыми жұмысымды 3 кезеңге бөлдім.

І кезең: тақырыпты таңдау.

ІІ кезең: тақырыпқа байланысты тарихи, математикалық шығармаларды жинап оны топтау.

ІІІ кезең: табылған ақпаратты талдау және өңдеу.

ІV кезең: жұмысты жазып, қорғау.

Зерттеу құралдары. Зерттеу құралдары: математикалық кітаптар, бұқаралық ақпарат, интернет желісі.

Зерттеу әдісі: Анализ, синтез, жобалау әдісі

Қорытынды: Сонымен қорытындылай келе Пифагор теоремасы көп жағдайда өте қажет. Мысалы: есептер шығаруда, үлкен құрылыстарда, теоремаларды дәлелдегенде. Сондықтан бұл теореманың қыр - сырын толығырақ әрі тереңірек білу қызығушылық тудырады.

Пифагор теоремасы - геометрияның аса маңызды теоремаларының бірі. Көптеген теоремалар мен формулалар сол арқылы дәлелденеді. Олардың кейбіреулері:

Сүйір бұрышқа қарсы орналасқан қабырға туралы теорема.
Доғал бұрышқа қарсы орналасқан қабырға туралы теорема.
Герон формуласы.
Екі нүктенің ара қашықтығының формуласы.
Призма, параллелепипед, пирамида жөніндегі теоремалар.

Бұл тізімді әрі қарай жалғастыра беруге болады. Пифагор теоремасы өмірде жиі қолданылады, оның кездеспейтін жері аз. Сондықтан оны математик қана емес, әрбір мәдениетті адам білуі қажет.

The summary

Theme: « To prove theorem Pifagor different ways ».

The purpose of research: to carry out research, that it is possible to prove theorem

Pifagor different ways.

Urgency of research: Theorem Pifagor takes the important place in development of mathematics; to like and to understand more deeply mathematics; to interest pupils.

Hypothesis : If during exploratory works to use different methods, scientific materials they will help{assist} development communicativeness, compiling to interest to mathematics.

Investigation phases:

І a stage: the Choice of a theme

ІІ a stage: Gathering of materials on a theme

ІІІ a stage: To make development of materials

ІV a stage: Protection

Materials of research: mathematical books, literary books, directories

Method of research: the analysis, synthesis, designing

The conclusion: Theorem Pifagor it is necessary for the decision of mathematical problems{tasks}; for construction; to prove theorems. Studying of theorem Pifagor from the different parties{sides} causes interest not only to mathematics, but also in a life of many people, whose speciality is connected with mathematics and to each person who considers{counts} itself formed and cultural.

Кіріспе

Еліміздің тәуелсіздігі бүгінгі күні қоғамымыздағы интеллектуалдық еңбек үлесінің өсуі нәтижесінде өмірге ертең араласатын жеткіншектердің білім деңгейіне, әр адамның қабілеті мен шығармашылық әлеуетінің дамуына, оның кәсіптік икемділігіне қойылатын талаптар да күннен күнге арта түсуде. Елбасы Н. А. Назарбаев Еуразия ұлттық университетінде оқыған лекциясында: «Білімді, сауатты адамдар - бұл ХХІ ғасырда адамзат дамуының негізгі қозғаушы күші» - деп атаған [1] .

Қазіргі заманғы білім берудің перспективалық міндеті - ол сындарлы ойлай білетін және ақпараттар ағынында бағдар ала білуге қабілетті адамдарды даярлау. Орта білім белсенді, білімді және табыстарға бағдарланған тұлғаларды тәрбиелеуге жауап береді. Оқушылар «ешқашан бастауды тоқтатпа, ешқашан тоқтауды бастама» деген ақиқаттан адаспауы тиіс [2] .

Математикалық ұғымдар, аксиомалар мен анықтамалар және қорытындылар (теоремалар және салдарлар) нақтылы өмірде бар болатын әртүрлі заттардың, онда болып жатқан құбылыстар мен өтіп жатқан процестердің өздеріне тән жалпы қасиеттерінің біздің санамызда бейнеленуі болып табылады. Академик А. Н. Колмогоров: «Математик әрқашан реалды құбылыстардың әртүрлі модельдерімен жұмыс жасайды. Оны, математик ретінде, қабылданған модель аясында қорытындылар орынды ма деген сұрақ ғана ойландырады. Егер де ол реалдылық пен оның математикалық моделінің арасындағы диалектикалық байланысты түсіндіру міндетінен бас тартса, бұл әсте жақсы емес» - деп көрсеткен болатын [3] .

«Айтушылардың сөзіне қарағанда ғылымның бұл саласын жоғары тұрғыдан зерттеп, қиқы-шойқы жерлерін түзеп, шалағай ережелерді ширатып, ақыл парасатына жүгіндіріп, үлкен ғылымға айналдырушы Пифагор болған» [4] .

Пифагор - арифметика, геометрия, астрономия, музыка ғылымдарына елеулі үлес қосқан ғалым. Оның арифметикадағы табыстары өте көп. Алайда Пифагордың есімін есімізге сала беретін, оны тарихта қалдырған ғылым геометрия болып табылады. Квадраттың диагоналы мен қабырғасы өлшемдес болмайтындығын, соған байланысты иррационал сандардың болатындығын алғаш рет Аггинанор ұлы Пифагор (580-500) тағайындаған.

Пифагордың ең басты еңбегі - Пифагор теоремасы [4] .

Менің осы тақырыпты таңдаған себебім, менің ойымша Пифагор теоремасы әлемдік құпиялардан да қызықтырақ. Пифагор теоремасы математика саласына елеулі үлес қосады және оның дамуына қажет. Сонымен қоса Пифагор теоремасы - геометрияның аса маңызды теоремаларының бірі. Көптеген теоремалар мен формулалар сол арқылы дәлелденеді. Пифагор теоремасы өмірде жиі қолданылады, оның кездеспейтін жері аз. Сондықтан мен осы теоремаға қызығушылық танытып, осы маңызы зор тақырыпты таңдап алдым.

Бұл жобаның мақсаты зерттеу жұмысында Пифагор теоремасын

зерттеп, басқа жолдармен дәлелдеу. Пифагор теоремасы математика

саласының дамуына қажет болғандықтан, бұл теореманы тереңірек ұғып,

түсіну. Оқушылардың математика пәніне қызығушылығын арттыру.

Пифагор теоремасын әр түрлі жолдармен дәлелдеуге болатынын көрсету.

Мектеп математика курсының мазмұнында қарастырылып отырған теорема не үшін керек екендігін оқушыларға барлық кездескен жағдайларда түсінікті болатындай етіп ашу.

Оқушылардың логикалық ой - қабілеттерін арттыру.

[1] - Назарбаев Н. Ә. Инновациялар мен оқу-білімді жетілдіру арқылы білім экономикасына // Егенмен Қазақстан, 27 мамыр, 2006, №2б [2] - Егемен Қазақстан, жалпыұлттық республикалық газет. №336 (25733), 14 қазан, 2009 жыл, 2б

[3] - Колмогоров А. Н. Современная математика и математика в современной школе // Математика в школе. - 1971. - №6. - С. 2-3.

[4] - Математика мен математиктер жайлы әңгімелер. М. Ө. Исқақов, С. Н. Назаров. Екінші кітап, «Мектеп», 1970, 315 бет.

2. 1. Пифагор теоремасы жайында

Көпбұрыштардың аудандарының қасиеттерін пайдалана отырып, біз тік бұрышты үшбұрыштың гипотенузасы мен катеттерінің арасындағы тамаша қатысты тағайындаймыз. Біз дәлелдейтін теорема Пифагор теоремасы деп аталып, геометриядағы негізгі теоремаға жатады [5] .

Теорема. Тік бұрышты үшбұрыштың гипотенузасының квадраты катеттерінің квадраттарының қосындысына тең [4] . Бұл сөйлем Пифагор теоремасының арифметикалық тұжырымдамасы деп аталады. Арифметикалық тұжырымдама бойынша гипотенузаны сипаттайтын санның квадраты катеттерді сипаттайтын сандардың квадраттарының қосындысына тең болады.

Ал бұрынғы оқулықтарда теореманың толық тұжырымдамасы мынандай:

Тік бұрышты үшбұрыштың гипотенузасына салынған квадраттың ауданы катеттеріне салынған квадраттардың аудандарының қосындысына тең болады [4] .

Гипотенузаға салынған квадратты төменгі жағына, катеттерге салынған квадраттарды жоғарғы жағына келтіріп, теореманың чертёжін салсаңыз, кілең түзу кесінділерден құралған фигура пайда болады. Бұл фигура «есек көпірі» деп аталып кеткен: латынша - «понс азинорум», французша- «лес понт аукс анез» (немісше- «ди эселбрюкке», орысша - «мост ослов») . Кейбіреулер оны шалбардың суреті сияқты деп есептеген. Орта ғасырлардағы мектептерде Пифагор теоремасын жыл бойы жаттайтын болған. Сонда жаттай - жаттай жалыққан шәкірттер былай деп әндетіп те қояды екен:

Пифагордың шалбары,

Соңымыздан қалмады.

Ышқыры кең, ауы тік,

Бір балағы тар-дағы [4] .

Осы бұрынғы оқулықтардағы теореманы негізге ала отырып, мен Пифагор теоремасын дәлелдеуді тік бұрышты үшбұрыштың гипотенузасын 3 - тен басталатын натурал сан, ал катеттерін нақты сандар жиынында қарастырдым. Яғни

с € Ν , а € R , в € R .

[5] -Геометрия 7-9. Л. С. Атанасян. Орыс аудармасы (Нүсіпбаев Т. ) «Рауан», 1992, 125 бет.

[4] -Математика мен математиктер жайындағы әңгімелер. М. Ө. Ысқақов. С. Н. Назаров. «Мектеп», 1970, 316 бет.

2. 2. Теореманы дәлелдеудің бірінші тәсілі

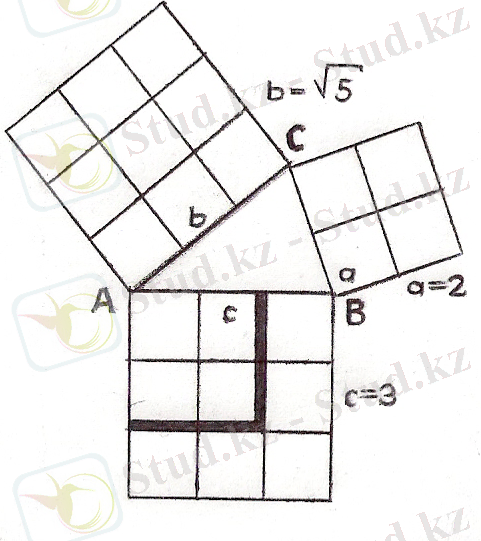
1 - сурет

Бірінші, гипотенуза 3 см болсын. Сонда Пифагор теоремасының формуласы $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ бойынша 3² = a ² + b² болады. 3 см - ге тең гипотенуза бойынша, катеттердің өлшемдерін жуықтап есептеу тәсілімен a = 2 см , b = √5 см деп аламын. Пифагор теоремасы бойынша формула $2^{2} + {(\sqrt{5}) }^{2} = 3^{2}$ $2^{2} + {(\sqrt{5}) }^{2} = 3^{2}$ немесе 9=4+5 натурал сандарына түрленеді. Бұл теңдіктің оң жағын қоса отырып, (4+5) квадраттардың аудандары 3 см - лік гипотенузаға салынған квадраттың ауданына тең шамалы екенін көреміз, яғни 9 см² = 9 см² (1 - сурет)

2. 3. Теореманы дәлелдеудің екінші тәсілі

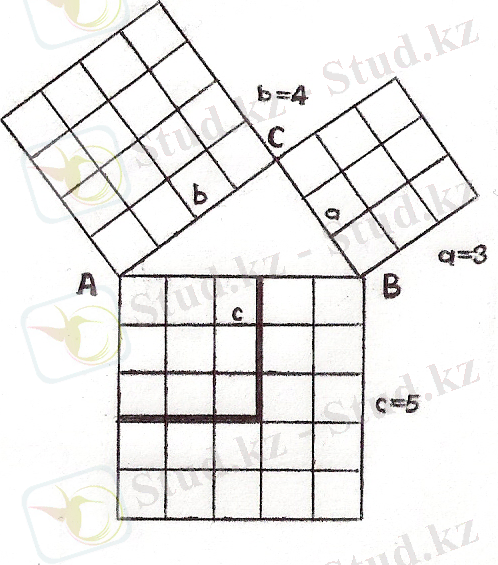
2 - сурет

Гипотенуза 5см-ге тең болса, аналитикалық теңдеу : $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$

берілген үшбұрыш бойынша: 5²= а²+b² жуықтап есептеу тәсілі бойынша

5² = √9 + √16 = 3² + 4², квадраттарды есептесек 25 = 9+16. Квадраттың ауданы см² түрінде берілгенде, тікбұрышты үшбұрыш гипотенузада 5 см-ге тең, оның а = 3см; b = 4см-ге тең катеттерінде құрылған.

25 = 9+16 теңдігінде үшбұрыштың катеттерінде орналасқан екі шаршының ауданын см² түрінде аламыз. Бұл гипотенузада орналасқан шаршының ауданына тең. Яғни 25 см² = 25см² екенін дәлелдедік (2 - сурет) .

2. 4. Теореманы дәлелдеудің үшінші тәсілі

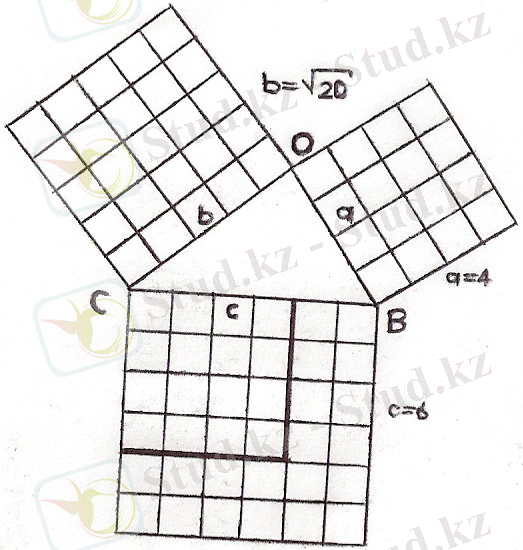
3 - сурет

Бұл суретте тікбұрышты ∆ АВС гипотенузасы 6 см болатын үшбұрышқа сәйкес катеттерін жуықтап есептейміз. Сонда катеттерге салынған квадраттардың аудандарының қосындысын гипотенузадағы квадраттың ауданына тең болуы керек. Аналитикалық теңдеу: $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ мынадай түрге айналады,

с² = 4² + (√ 20 ) ² квадраттарын есептегенде 36 см² = 16см² +20см ². Катеттердің квадраттарының ауданын қосу арқылы, үлкен квадраттың ауданын табамын, ол сөзсіз гипотенузада орналасқан квадраттың ауданына тең.

36 см² = 36 см² екені дәлелденді. (3 - сурет) .

2. 5. Теореманы дәлелдеудің төртінші тәсілі

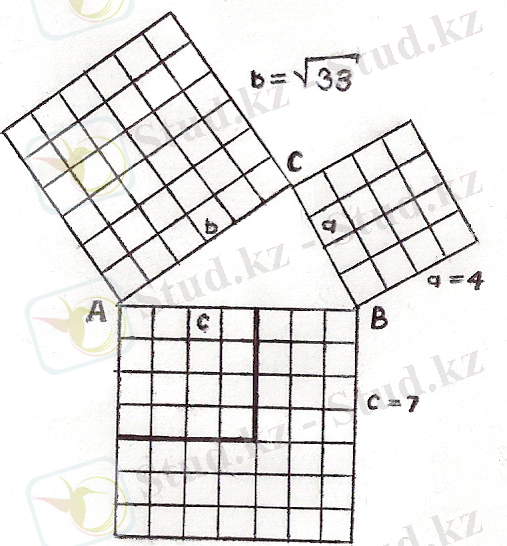
4 - сурет

Тікбұрышты ∆ АВС берілген. Оның гипотенузасы

7 см-ге тең. Катеттердің өлшемін есептеу арқылы гипотенузадағы квадраттың ауданы, катеттерге салынған квадраттардың ауданының қосындысына тең екенін анықтап, төмендегідей теңдік аламын: $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ ; 7²=4²+(√33) ²;

49 = 16+33; 49 см² = 49 см² болатыны дәлелденді.

(4 - сурет) .

2. 6. Теореманы дәлелдеудің бесінші тәсілі

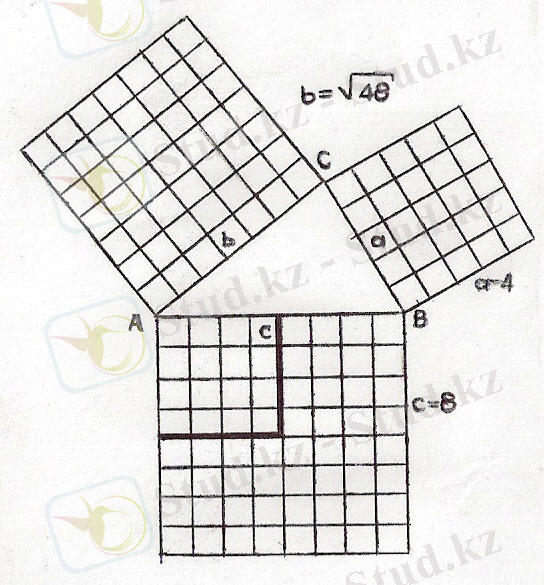
5 - сурет

Тікбұрышты ∆ АВС берілген. Оның гипотенузасы

8 см-ге тең. Пифагордың теоремасын дәлелдей отырып, $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ ;

8 ² = 4²+(√48) ² ; 64 = 16 + 48 ; 64 см² = 64 см $²$ $²$ екенін дәлелдедім. (5 - сурет) .

2. 7. Теореманы дәлелдеудің алтыншы тәсілі

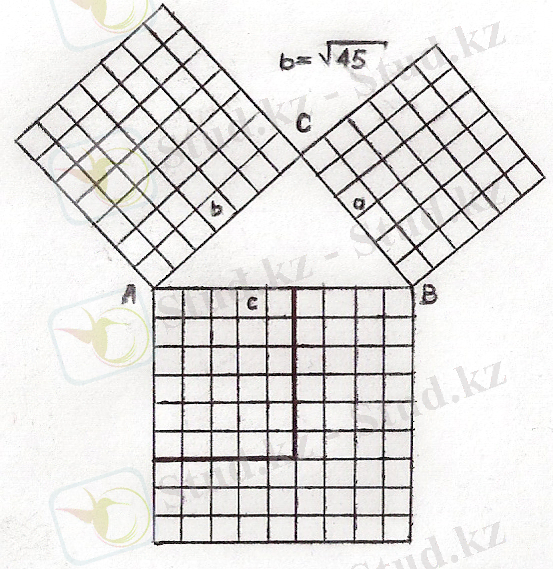
6 - сурет

Тікбұрышты ∆ АВС берілген. Оның гипотенузасы 9 см-ге тең болғанда $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ ; 6² + (√45) ² = 9²; 36 + 45 = 81; 81см² = 81см² екенін дәлелдедім.

(6 - сурет) .

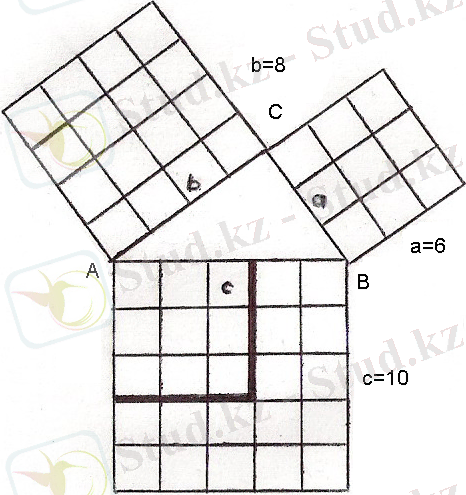2. 8. Теореманы дәлелдеудің жетінші тәсілі

7 - сурет

Тікбұрышты ∆ АВС берілген. Оның гипотенузасы 10 см-ге тең. Бұл теңдікті былай шешеміз: $a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ ; 6² + 8² = 10²; 36 + 64 = 100; 100 см² = 100 см² екенін дәлелдедім (7 - сурет) .

2. 9. Сипаттау № 1

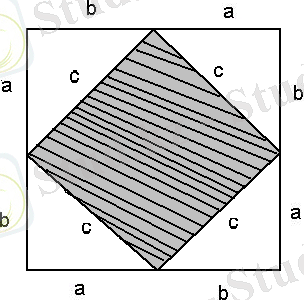
10 - сурет

Осы квадраттың S ауданы (a + b ) ² - қа тең. Квадрат әрқайсысының 1/2аb болатын төрт тең тік бұрышты үшбұрыштан және қабырғасы с - ға тең квадраттан тұрады, сол себепті

S = 4*1/2ab + c² = 2ab + c² .

Осылайша,

(a + b ) ² = 2ab + c²,

осыдан

$a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ .

[5] -Геометрия 7-9. Л. С. Атанасян. Орыс аудармасы (Нүсіпбаев Т. ) «Рауан», 1992, 125 бет.

2. 10. Сипаттау № 2

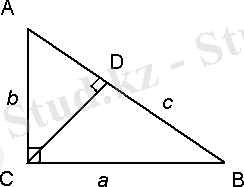
11 - сурет

Тікбұрышты ∆ АВС берілген. С төбесінен СD биіктік жүргіземіз (10-сурет) . Косинустың анықтамасы бойынша cos (∟А) = АС .

АВ

Ал АСD тік бұрышты үшбұрышынан cos (∟А) = AD теңдігін аламыз.

АС

Осыдан АВ ∙ АD = AC² болатынын көреміз. Осы сияқты cos (∟В) = BD = BC

BC AB теңдігінен АВ ∙ ВD = ВC² теңдігі шығады. Осы шыққан теңдіктерді мүшелеп қосып, АВ + ВD = АВ екенін ескерсек,

AC² + ВC² = АВ ∙ АD + АВ ∙ ВD = АВ(АD + ВD) = АВ²

теңдігін аламыз. Теорема дәлелденді [6] .

[6] -Геометрия 8. Ә. Н. Шыныбеков. «Атамұра», 2004, 58 - бет

2. 11. Сипаттау № 3

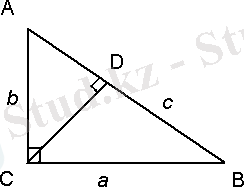
12 - сурет

АВС - берілген тік бұрышты үшбұрыш, оның тік бұрышы С болсын Тік С бұрышының төбесінен СD биіктігін жүргіземіз (11 - сурет) .

Косинустың анықтамасы бойынша cos A = AD = AC .

AC AB

Бұдан АВ ∙ АD = AC². Осылайша cos В= BD = BC .

ВС AB

Бұдан АВ ∙ ВD = ВC². Шыққан теңдіктерді мүшелеп қосып және де

АD + ВD = AB екенін ескерсек, былай болып шығады:

АС² + ВC² = AB (AD + BD) = AB².

Теорема дәлелденді [7] .

[7] - Геометрия 7 - 11. А. В. Погорелов. Қазақша аудармасы Қаниев С., Бөкейханов Р. және т. б. «Рауан», 1995 - 384 бет.

2. 12. Сипаттау № 4

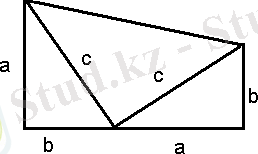
13 - сурет

Биіктігі горизонталь орналасқан және а + в қосындыға тең, табандары а және в катеттерге тең тік бұрышты трапеция саламыз. Трапецияны катеттері а және в болатын екі үшбұрышқа, катеттері с болатын бір тең бүйірлі тік бұрышты үшбұрышқа ажыратамыз. Сонда үш тік бұрышты үшбұрыштың аудандарының қосындысы трапецияның ауданындай болуға тиіс:

1/2 (а + в) (а + в) = 1/2 ав + 1/2 с² + 1/2 ав [4] ,

$a^{2} + b^{2} = c^{2}$ $a^{2} + b^{2} = c^{2}$ .

[4] - Математика мен математиктер жайлы әңгімелер. М. Ө. Исқақов, С. Н. Назаров. Екінші кітап, «Мектеп», 1970, 315 бет.

2. 13. Сипаттау № 5

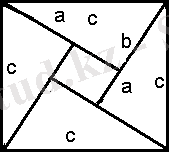
14 - сурет

АВС үшбұрышы ішінде қалатындай етіп, гипотенузаның квадратын саламыз, содан кейін түзулер жүргізіп, берілген үшбұрышқа тең 3 үшбұрыш саламыз. Үшбұрыштардың аралығында қабырғасы а - в айырмаға тең кішкене квадрат құралады. Бұлардың аудандарын салыстырып,

с² = (а - в ) ² +( 4 * 1/2 ав)

теңдікке келеміз, одан:

$a^{2} + b^{2} = c^{2}$ .

[4] - Математика мен математиктер жайлы әңгімелер. М. Ө. Исқақов, С. Н. Назаров. Екінші кітап,

«Мектеп», 1970, 315 бет.

2. 14. Сипаттау № 6

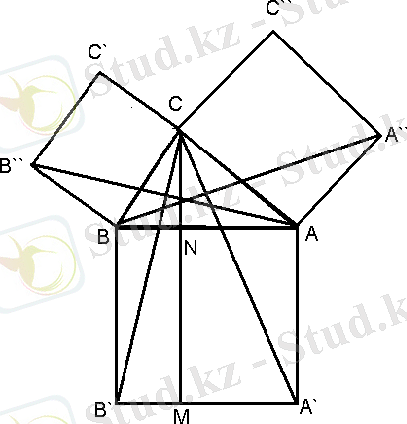
15 - сурет

Тікбұрышты АВС үшбұрышының қабырғаларына ВСС`B``, ACC``A``, ABB`A`

Квадраттарды салайық, оларды үшбұрыштың сыртқы жағына орналастырайық. Тік бұрыштың С төбесінен гипотенузаға перпендикуляр түзу жүргізіп, оның АВ гипотенузамен қиылысатын нүктесін N әрпімен, квадраттың A`B` қабырғасымен қиылысатын нүктесін М әрпімен белгілейік. Сонда ВСС`B`` квадраттың ауданы

гипотенузадағы квадраттың бір бөлігі - ВB``МN тік төртбұрыштың ауданына,

ACC``A`` квадраттың ауданы гипотенузадағы квадраттың екінші бөлігі - AA`МN тік төртбұрыштың ауданына тең болады. Алдымен осыны дәлелдейік.

Түзулер арқылы А нүктесін B`` нүктеге, С нүктесін B` нүктеге қосайық. Мұның нәтижесінде өзара тең АВB`` және ВСВ` доғал бұрышты үшбұрыштар пайда болады. Өйткені:

АВB`` үшбұрышының ВB`` қабырғасы ВСВ` үшбұрышының ВС қабырғасына тең, екеуі деа, яғни ВСС`B`` квадраттың қабырғалары,
АВB`` үшбұрышының АВ қабырғасы ВСВ` үшбұрышының ВB` қабырғасына тең, екеуі дес, яғни ABB`A` квадраттың қабырғалары,

3) ∟АВB`` = 90˚ + ∟АВС, ∟CВB` = 90˚ + ∟АВС, сондықтан ∟АВB``=∟CВB`. Олай болса, үшбұрыштардың теңдігінің бірінші белгісі бойынша жоғарыда айтылған АВB`` және ВСВ` үшбұрыштары өз ара тең, олардың аудандары да тең:

∆ АВB``= ∆ ВСВ`.

B``В қабырғаны АВB`` доғал бұрышты үшбұрыштың табаны ретінде алып, оның созындысына А төбеден биіктік жүргізсек, ол биіктіктің ұзындығы ВС-ге тең болады (чертежді күрделендіріп жіберетіндіктен, биіктік көрсетілмеген, бірақ оны түсіну оңай, ол АА` МN тік төртбұрышының ішінде орналасады, ВС,

B``С` қабырғаларға параллель және тең болады) . Сондықтан : АВB`` үшбұрышының ауданы :

S = 1/2 ВB`` * ВС = 1/2а².

Демек, АВB`` үшбұрышының ауданы ВСС`В`` квадраттың ауданының жартысындай.

ВВ` қабырғаны ВСВ` доғал бұрышты үшбұрыштың табаны ретінде алып, оның созындысына С төбеден биіктік жүргізсек, ол биіктік (ВN және В`М кесінділерге параллель және тең, ВСС`В`` квадраттың ішінде орналасады) ВN-ге тең болады. Сондықтан : ВСВ` үшбұрышының ауданы:

S = 1/2 ВB` * ВN.

Мұндағы ВB` * ВN көбейтіндісі ВB`МN тік төртбұрыштың ауданын өрнектейді. Олай болса, ВСВ` үшбұрышының ауданы ВB`МN тік төртбұрыштың ауданының

жартысындай болады.

Сөйтіп, ВB`МN тік төртбұрышының ауданы ВСВ` үшбұрышының ауданынан екі есе артық, ВСС`В`` квадраттың ауданы АВB`` үшбұрышының ауданынан

екі есе артық болып шықты. Ал айтылып отырған үшбұрыштар өз ара тең. Ендеше ВСС`В`` квадраттың ауданы ВB`МN тік төртбұрыштың ауданына тең болады.

Дәл осылай, В нүктесін А`` нүктеге, С нүктесін А` нүктеге кесінділер арқылы қосып, доғал бұрышты АВА`` және АСА` үшбұрыштарының теңдігін дәлелдеуге болады. Одан әрі АСС``А`` квадраттың ауданы АВА`` үшбұрышының ауданынан екі есе артық, АА` МN тік төртбұрыштың ауданы АСА` үшбұрышының ауданынан екі есе артық болатындығын, соның салдарынан АСС``А`` квадраттың ауданы АА` МN тік төртбұрышының ауданына тең болатындығын дәледеуге болады.

23

ВСС`В`` квадраттың ауданы ВB`МN тік төртбұрыштың ауданына, АСС``А`` квадраттың ауданы АА` МN тік төртбұрыштың ауданына тең болып шықты. Албұл екі тік төртбұрыштың аудандарының қосындысы гипотенузаға салынған

АВВ`А` квадраттың ауданына тең. Сондықтан:

катеттерге салынған квадраттардың аудандарының қосындысы гипотенузаға салынған квадраттың ауданындай болады.

Теорема дәлелденді [4] .

[4] - Математика мен математиктер жайлы әңгімелер. М. Ө. Исқақов, С. Н. Назаров.

Екінші кітап, «Мектеп», 1970, 315 бет.

Қорытынды.

Сонымен, қорытындылай келе, Пифагор теоремасы көп жағдайда өте қажет. Мысалы: есептер шығаруда, үлкен құрылыстарда, теоремаларды дәлелдегенде. Сондықтан бұл теореманың қыр - сырын толығырақ әрі тереңірек білу қызығушылық тудырады.

Математика тарихшыларының зерттеулері бойынша теореманы алғаш рет

Пифагор дәлелдеген. Оның нақты дәлелдемесі бізге жетпеген. Болжам

бойынша Пифагор бұл теореманы ұқсас үшбұрыштар арқылы дәлелдеген

болу керек.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.