Элементар функциялардың туындылары: геометриялық және механикалық мағыналары


Қазақстан Республикасының Білім және ғылым министрлігі
М. Өтемісов атындағы Батыс-Қазақстан мемлекеттік университеті
Физика -математика факультеті
Физика және математика кафедрасы
Курстық жұмыс
Тақырыбы: «Туынды. Элементар фунциялардың туындысы, геометриялық және механикалық мағынасы»
Орындаған: Беркінов Ж. Б.
Жетекші: Физика-математика
кафедрасының оқытушысы,
магистр Мухамбетова Б. Ж.
Орал, 2017 жыл
МАЗМҰНЫ
Кіріспе . . . 3
1 Элементар функцияның туындысы
1. 1 Анықтамалар мен түсініктер . . . 5
2. Элементар функциялардың геометриялық және механикалық мағынасы . . . 8
2. 1Элементар функцияның туындысын анықтама арқылы есептеу . . . 16
Қорытынды . . . 18
Пайдаланылған әдебиеттер тізімі . . . 20
Кіріспе
Математика - нақты өмірдегі сандық қатынастар мен кеңістіктік формалар туралы ғылым. Математикада математикалық модельдер зерттеледі. Ол нақты құбылыстардың тура математикалық модельдері болуымен қатар осы модельдерді зерттеуге арналған (структуралар) объект болуы мүмкін. Бір математикалық модель тура мазмұны жағынан бір-бірінен қашық жатқан нақты құбылыстардың қасиеттерін көрсетуі мүмкін. Мысалы, бір дифференциалдық теңдеу халықтың өсу процессін де жəне макроэкономикалық динамикасын да көрсетеді. Математика үшін қарастырылып отырған объектілердің табиғи мəні емес, олардың арасындағы қатынастардың маңызы зор. Математика жаратылыс ғылымдарында, инженер-техникалық жəнегуманитарлық зерттеулерде маңызды роль атқарады. Ол көптеген білім бөлімдерінде тек қана сандық есептеу жасау үшін ғана емес, сонымен қатар дəлірек зерттеудің тəсілі жəне ұғымдар мен проблемалардың шекті тура тұжырымдарын беру құралы болады. Адам өміріндегі əртүрлі салалардағы прогресс жетілдірілген логикалық жəне есептеу аппараты бар қазіргі замандағы математикасыз мүмкін емес. Математикада ең маңызды ұғымдардың бірі - функция туындысы ұғымы болып табылады. Туындылар және олардың функциялары математикалық анализ курсының ең негізгі бөлімі болып табылады. Бұл терминмен оқушылар «Алгебра және анализ бастамалары» атты курсында танысады. Туынды ұғымы бастапқыда шек түрінде анықталады. Бұл жерде оқушыларға «Шек» терминін кезінде Ньютон еңгізгенін, оның lim белгіленуі - латынның limes (меже, шекара) деген сөзінің қысқарған түрі екенін түсіндіріп, айта кету керек. Математикада шексіз аздардың алатын орны ерекше екенін айта кетіп, сондықтан да математикалық анализді кейде шексіз аздар анализі деп атайтынын айтып кеткен жөн. Бірінші сабақта туынды ұғымын еңгізбес бұрын келесі есептерді қарастырған жөн. Олар: химиялық реакцияның жылдамдығы, токтың лездік күші, денелердің лездік жылдамдығын табу, дененің жылуы, қисыққа жанама жүргізу т. с. с. солардың кейбіреулеріне тоқталайық. Функция туындысы түсінігін лездік жылдамдықты анықтау мен жанама жөніндегі есептерді шешуден бастайды. Туынды - дифференциалдық есептеулердің х аргументі өзгерген кездегі f(x) функциясының өзгеру жылдамдығымен сипатталатын негізгі түсінігі. Кез келген х үшін қатынасының шегі арқылы анықталатын функция туынды деп аталады және y΄, f΄(x), түрінде белгіленеді. туындысы бар функция үзіліссіз. Берілген аралықтың барлық нүктелерінде туындысы болмайтын үзіліссіз функциялар да болады. “ Туынды” терминін (1797) және оның белгіленулерін (1770, 1779) Ж. Лагранж, ал түрінде жазылуын Г. Лейбниц енгізген (1675) .
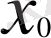 нүктесі тығыздық нүктесі болып табылатын жиынның нүктелері арқылы х→х0 ұмтылған кездегі қатынасының шегі асимптоталық туынды деп аталады. Элементар функциялар - көпмүшеліктер, рационал функциялар, көрсеткіштік, дәрежелік, логарифдік және тригонометриялық функциялар, кері тригонометриялық функциялар, осымен қатар, аталған функциялардан арифметикалық төрт амалды қолдану және функциялар суперпозициясын құру арқылы жасалатын функциялар класы.
нүктесі тығыздық нүктесі болып табылатын жиынның нүктелері арқылы х→х0 ұмтылған кездегі қатынасының шегі асимптоталық туынды деп аталады. Элементар функциялар - көпмүшеліктер, рационал функциялар, көрсеткіштік, дәрежелік, логарифдік және тригонометриялық функциялар, кері тригонометриялық функциялар, осымен қатар, аталған функциялардан арифметикалық төрт амалды қолдану және функциялар суперпозициясын құру арқылы жасалатын функциялар класы.
Жұмыстың мақсаты: элементар функциялардың туындысын теориялық тұрғыда негіздеп, есептер щығару әдістемесін жетілдіру. Жұмыстың міндеті: элементар функцияның туындысы, оның геометриялық және механикалық мағынасы тақырыптарының оқулықтарда баяндалуына талдауды жүзеге асыру.
1 Элементар функцияның туындысы
1. 1 Анықтамалар мен түсініктер
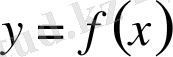 функциясы
функциясы
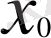 нүктесінде және оның белгілі бір маңайында анықталсын. Егер
нүктесінде және оның белгілі бір маңайында анықталсын. Егер
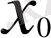 нүктесіндегі аргумент өсімшесі
нүктесіндегі аргумент өсімшесі
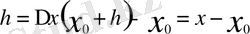
болса, онда осы өсімше тудырған (немесе осы өсімшеге сәйкес) функция өсімшесі
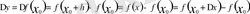
арқылы белгіленетін еді. Аталған өсімшелер
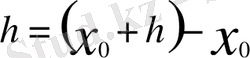 санына тәуелді болатындықтан, олар сәйкес
санына тәуелді болатындықтан, олар сәйкес
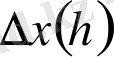 және
және
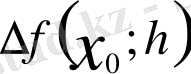 символдарымен белгіленеді. Алайда ықшамдылық үшін жиі қолданылатын
символдарымен белгіленеді. Алайда ықшамдылық үшін жиі қолданылатын
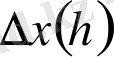 және
және
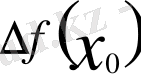 символдарын пайдаланамыз.
символдарын пайдаланамыз.
Анықтама.
Егер
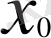 нүктесіндегі
нүктесіндегі
 аргумент өсімшесіне сәйкес алынған
аргумент өсімшесіне сәйкес алынған
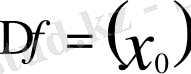 - функция өсімшесінің осы
- функция өсімшесінің осы
 аргумент өсімшесіне қатынасының h →0 ұмтылғандағы шегі бар болса, онда ол шек
аргумент өсімшесіне қатынасының h →0 ұмтылғандағы шегі бар болса, онда ол шек
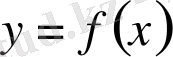 функциясының
функциясының
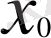 нүктедегі туындысы деп аталады
нүктедегі туындысы деп аталады
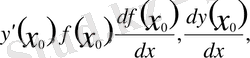
т. с. с. символдардың бірімен белгіленеді. Сонымен,
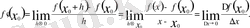
Егер (1) шек +∞ немесе −∞ тең болса, онда
f
функциясының
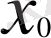 нүктесінде ақырсыз туындысы бар, атап айтқанда, егер
нүктесінде ақырсыз туындысы бар, атап айтқанда, егер
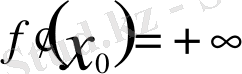 болса плюс ақырсыз, ал
болса плюс ақырсыз, ал
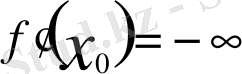 болса минус ақырсыз туындысы бар дейді. Егер
болса минус ақырсыз туындысы бар дейді. Егер
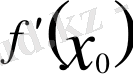 туындыcы нақты санға, немесе +∞ немесе −∞ ақырсыздықтарының біріне тең болса, онда функцияның
туындыcы нақты санға, немесе +∞ немесе −∞ ақырсыздықтарының біріне тең болса, онда функцияның
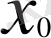 нүктеде кең мағыналы туындысы бар дейміз. Егер (1) теңдіктегі шектер h→0, h>0 (яғни
нүктеде кең мағыналы туындысы бар дейміз. Егер (1) теңдіктегі шектер h→0, h>0 (яғни
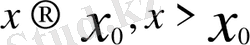 ) жағдайында қарастырылса, онда шек (ол бар болса)
f
функциясының
) жағдайында қарастырылса, онда шек (ол бар болса)
f
функциясының
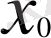 нүктедегі оң жақ туындысы. Ал, h→0, h<0 (яғни
нүктедегі оң жақ туындысы. Ал, h→0, h<0 (яғни
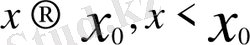 ) жағдайында қарастырылса, онда шек (бар болса)
f
функциясының
) жағдайында қарастырылса, онда шек (бар болса)
f
функциясының
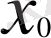 нүктедегі сол жақ туындысы деп аталады және сәйкес
нүктедегі сол жақ туындысы деп аталады және сәйкес
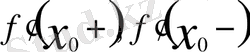 арқылы белгіленеді:
арқылы белгіленеді:
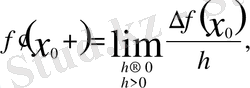
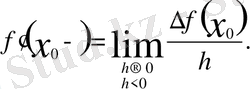
Функцияның 0 x нүктесінде туындысы бар болуы үшін,
1)
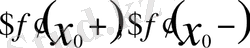 және 2)
және 2)
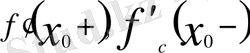
шарттарының орындалуы қажетті және жеткілікті:
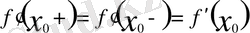
Мысал.
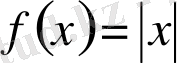 функциясы кез келген нүктеде үзіліссіз, өйткені
функциясы кез келген нүктеде үзіліссіз, өйткені
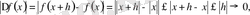
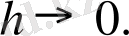
Бірақ оның х=0 нүктесінде туындысы жоқ. Расында да, бұл нүктеде
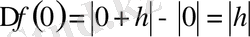 ескерсек
ескерсек
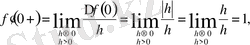
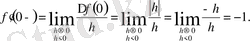
Функцияның х=0 нүктесінде біржақты туындылары бар, бірақ,
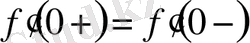 болғандықтан, оның бұл нүктеде туындысы жоқ. Сонымен, функция нүктеде үзіліссіз болғанымен, осы нүктеде функцияның туындысы болмауы мүмкін екен. Ал бұған кері тұжырым басқаша: x нүктесінде ақырлы туындысы бар функция осы нүктеде үзіліссіз болады. Шынында да, x нүктесінде (1) ақырлы шек бар болса, онда оны келесі түрде:
болғандықтан, оның бұл нүктеде туындысы жоқ. Сонымен, функция нүктеде үзіліссіз болғанымен, осы нүктеде функцияның туындысы болмауы мүмкін екен. Ал бұған кері тұжырым басқаша: x нүктесінде ақырлы туындысы бар функция осы нүктеде үзіліссіз болады. Шынында да, x нүктесінде (1) ақырлы шек бар болса, онда оны келесі түрде:
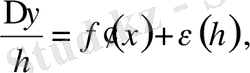
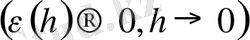
жаза аламыз. Бұл теңдіктен
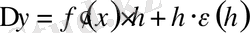 ал бұдан
ал бұдан
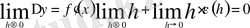 аламыз.
аламыз.
Демек, функция x нүктесінде үзіліссіз.
Салдар.
Егер
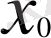 нүктесі
f
функциясының үзіліс нүктесі болса, онда осы нүктеде оның
ақырлы туындысы
болмайды. Ақырсыз туындылар үшін басқаша:
f
функциясының
нүктесі
f
функциясының үзіліс нүктесі болса, онда осы нүктеде оның
ақырлы туындысы
болмайды. Ақырсыз туындылар үшін басқаша:
f
функциясының
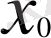 үзіліс нүктесінде де ақырсыз туындысы бар болуы мүмкін.
үзіліс нүктесінде де ақырсыз туындысы бар болуы мүмкін.
Мысалы,
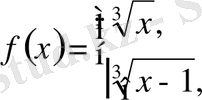
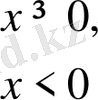 функциясының x=0 үзіліс нүктесінде плюс ақырсыз туындысы бар (тексеріңіз) .
функциясының x=0 үзіліс нүктесінде плюс ақырсыз туындысы бар (тексеріңіз) .
Ал егер (1) шек
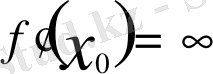 болса, онда функцияның
болса, онда функцияның
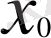 нүктесінде туындысы жоқ деп қабылдаймыз. Өйткені олай болмаса, онда ол кейбір математикалық тұжырымдарды (мысалы,
нүктесінде туындысы жоқ деп қабылдаймыз. Өйткені олай болмаса, онда ол кейбір математикалық тұжырымдарды (мысалы,
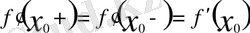 теңдіктерін және 42-45-суреттер мен олардың түсініктемелерін қараңыз), бірқатар теоремаларды (мысалы, орта мән туралы теоремалар) қарама-қайшылыққа әкеледі. Келтірілген тұжырымдар біржақты туындылар үшін де орындалады.
теңдіктерін және 42-45-суреттер мен олардың түсініктемелерін қараңыз), бірқатар теоремаларды (мысалы, орта мән туралы теоремалар) қарама-қайшылыққа әкеледі. Келтірілген тұжырымдар біржақты туындылар үшін де орындалады.
2 Элементар функциялардың геометриялық және механикалық
мағынасы
Лездік жылдамдылық.
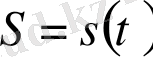 функциясы нүктенің түзу сызықты қозғалысының заңдылығын көрсетсін (S - нүктенің t уақыт кезеңіндегі жүрген жолы) . Нүктенің
функциясы нүктенің түзу сызықты қозғалысының заңдылығын көрсетсін (S - нүктенің t уақыт кезеңіндегі жүрген жолы) . Нүктенің
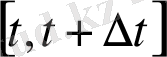 уақыт аралығында жүрген жолы
уақыт аралығында жүрген жолы
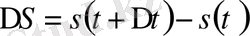 Оның осы уақыт ішіндегі
орташа
жылдамдығы
Оның осы уақыт ішіндегі
орташа
жылдамдығы
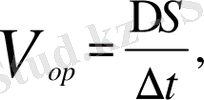 ал t уақыт кезеңіндегі
лездік
жылдамдығы
ал t уақыт кезеңіндегі
лездік
жылдамдығы
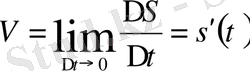 тең.
тең.
Ток күші. Q=f(t) функциясы t уақыт кезеңіндегі өткізгіштің қимасынан өтетін ток мөлшерін көрсетсін. Онда
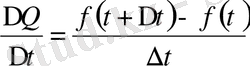
шамасы
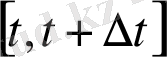 уақыт аралығындағы токтың орта күшін, ал
уақыт аралығындағы токтың орта күшін, ал
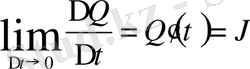
шамасы t уақыт кезеңіндегі ток күшін көрсетеді.
Туындының геометриялық мағынасы.
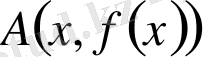 - тік бұрышты
Oxy
декарт координаттар жүйесінде берілген
- тік бұрышты
Oxy
декарт координаттар жүйесінде берілген
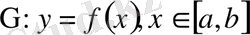 үзіліссіз қисықтың нүктесі болсын. (a, b) аралығында жатқан кез келген
үзіліссіз қисықтың нүктесі болсын. (a, b) аралығында жатқан кез келген
 нүктені алып
нүктені алып
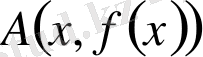 мен
мен
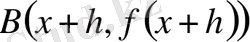 нүктелерінен өтетін S түзуін жүргіземіз және оның бағытын, осы түзу мен
Оx
өсінің оң бағыты арасындағы β бұрышы
сүйір
болатындай етіп таңдаймыз
нүктелерінен өтетін S түзуін жүргіземіз және оның бағытын, осы түзу мен
Оx
өсінің оң бағыты арасындағы β бұрышы
сүйір
болатындай етіп таңдаймыз
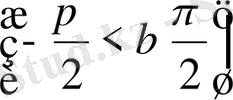 Бұл түзуді
қиюшы
(оны қою S әрпімен белгілейміз), ал β бұрышын - қиюшының Оx өсіне
көлбеу бұрышы
деп атаймыз (39- суретте, h > 0; 40-суретте, h < 0 ) .
Бұл түзуді
қиюшы
(оны қою S әрпімен белгілейміз), ал β бұрышын - қиюшының Оx өсіне
көлбеу бұрышы
деп атаймыз (39- суретте, h > 0; 40-суретте, h < 0 ) .
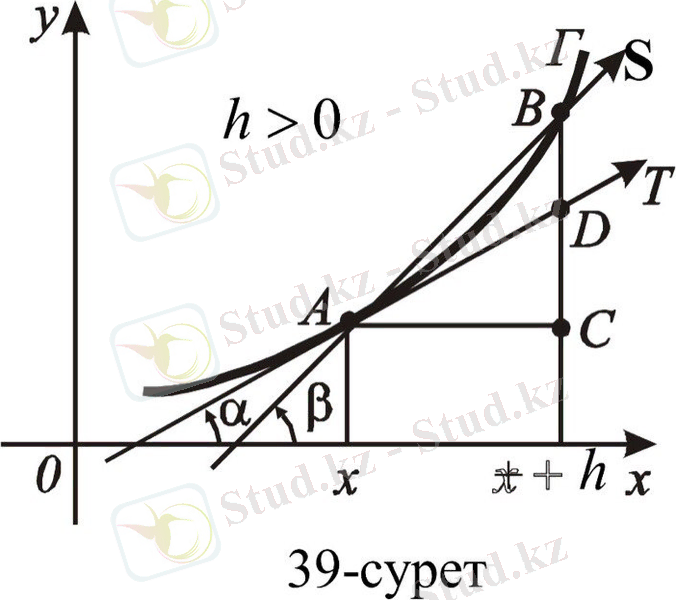
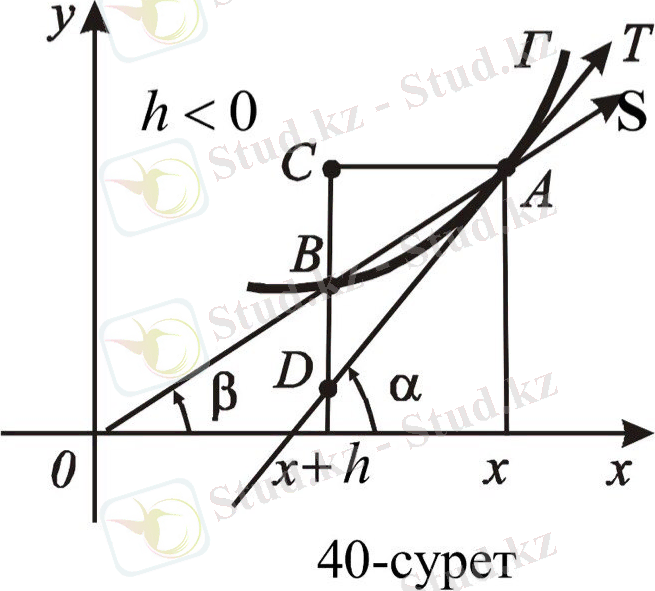
Қиюшы, абсциссалары x және x + h тең нүктелер арқылы өтетіндіктен, оның еңкею бұрышын
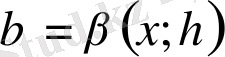 арқылы белгілейміз. Егер h→0 ұмтылғанда, S қиюшының
арқылы белгілейміз. Егер h→0 ұмтылғанда, S қиюшының
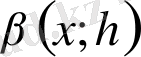 көлбеу бұрышы α санына ұмтылса, онда S қиюшы көлбеу бұрышы α-ға тең Т бағытталған түзуге ұмтылады.
көлбеу бұрышы α санына ұмтылса, онда S қиюшы көлбеу бұрышы α-ға тең Т бағытталған түзуге ұмтылады.
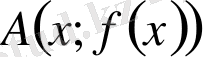 нүктесі арқылы өткен Т түзуінің α көлбеу бұрышының мәндері,
нүктесі арқылы өткен Т түзуінің α көлбеу бұрышының мәндері,
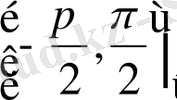 кесіндісінде жатады.
кесіндісінде жатады.
Анықтама.
Егер
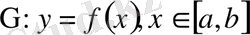 қисығындағы
қисығындағы
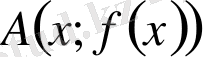 және
және
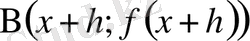 нүктелерінен өтетін қиюшының көлбеу бұрышының h→0 ұмтылғандағы шегі бар және ол шек
нүктелерінен өтетін қиюшының көлбеу бұрышының h→0 ұмтылғандағы шегі бар және ол шек
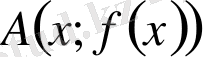 нүктесі арқылы өткен T бағытталған түзудің көлбеу бұрышына тең болса, онда бағытталған T түзуі Г қисығының
нүктесі арқылы өткен T бағытталған түзудің көлбеу бұрышына тең болса, онда бағытталған T түзуі Г қисығының
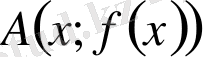 нүктесіндегі
жанамасы
деп аталады.
нүктесіндегі
жанамасы
деп аталады.
Аналитикалық геометриядан,
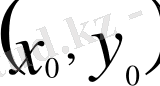 нүктесі арқылы өтетін, бұрыштық коэффициенті
нүктесі арқылы өтетін, бұрыштық коэффициенті
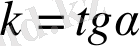 тең түзудің теңдеуі
тең түзудің теңдеуі
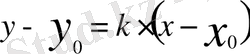 түрінде жазылатыны белгілі. Олай болса,
түрінде жазылатыны белгілі. Олай болса,
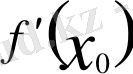 ақырлы болса,
ақырлы болса,
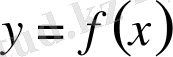 қисығының
қисығының
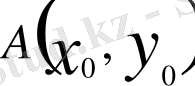 нүктесіндегі жанамасының теңдеуі
нүктесіндегі жанамасының теңдеуі
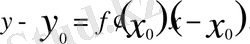
ал нормалінің теңдеуі
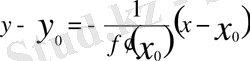
түрінде жазылады. Егер
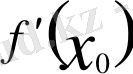 ақырсыз болса, онда жанаманың теңдеуі
ақырсыз болса, онда жанаманың теңдеуі
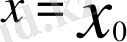 , ал нормальдің теңдеуі
, ал нормальдің теңдеуі
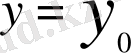 түрінде болады.
түрінде болады.
Енді ақырсыз туындыға қатысты келесі төрт маңызды жағдайды атап өтеміз:
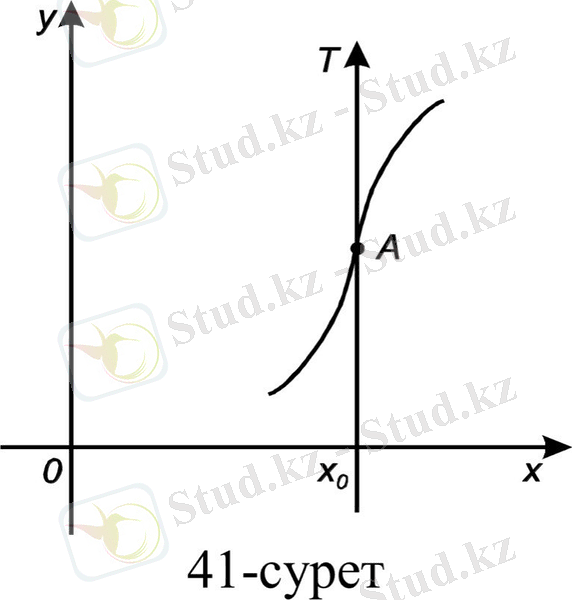
1)
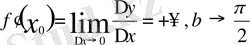 (функция туындысы бар; жанама
(функция туындысы бар; жанама
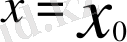 және ол оу өсімен бағыттас 41-сурет) ;
және ол оу өсімен бағыттас 41-сурет) ;
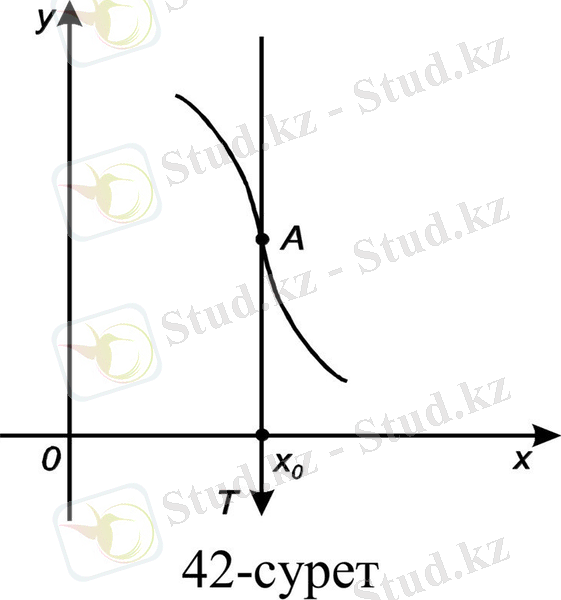
2)
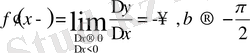 (функция туындысы бар; жанама
(функция туындысы бар; жанама
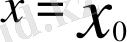 және ол оу өсіне қарама қарсы бағытталған (42-сурет) ;
және ол оу өсіне қарама қарсы бағытталған (42-сурет) ;
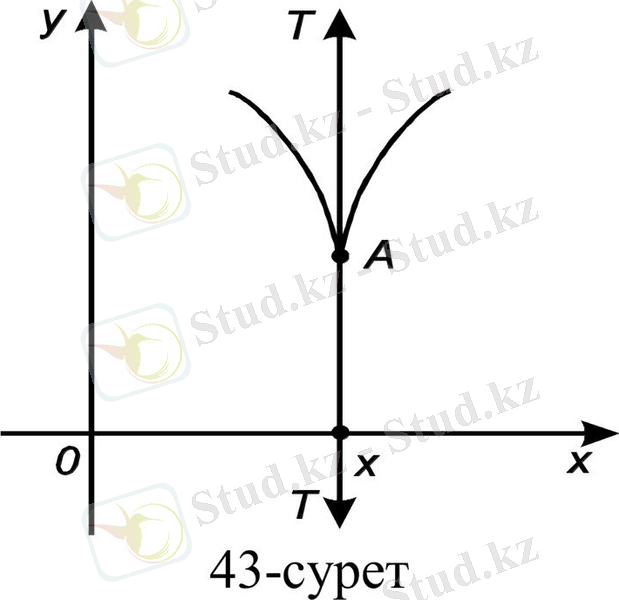
3)
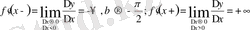
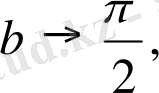 яғни
яғни
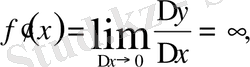 демек, функцияның туындысы жоқ. Мұнда сол жақ, оң жақ жанамалар x өсіне перпендикуляр және олар сәйкес төмен және жоғары бағытталған, яғни х нүктесінде жанама жоқ (43-сурет) ;
демек, функцияның туындысы жоқ. Мұнда сол жақ, оң жақ жанамалар x өсіне перпендикуляр және олар сәйкес төмен және жоғары бағытталған, яғни х нүктесінде жанама жоқ (43-сурет) ;
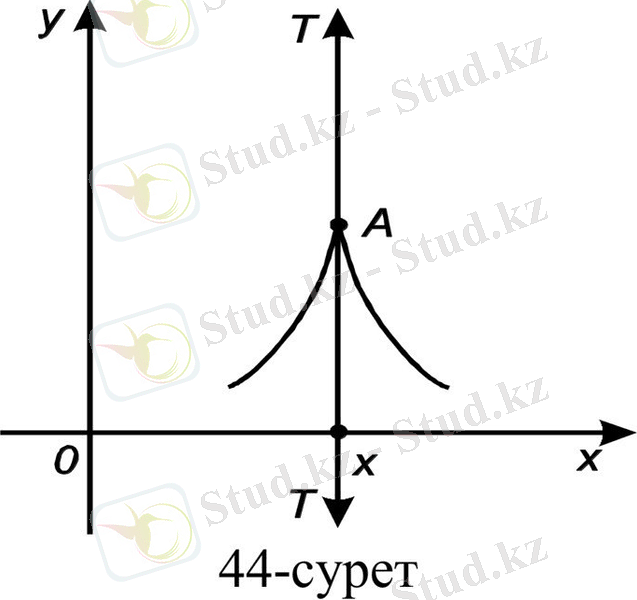
4)
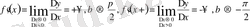 яғни
яғни
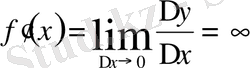 демек, функцияның туындысы жоқ. Мұнда сол жақ, оң жақ жанамалар x өсіне перпендикуляр және олар сәйкес жоғары және төмен бағытталған (44-сурет) .
демек, функцияның туындысы жоқ. Мұнда сол жақ, оң жақ жанамалар x өсіне перпендикуляр және олар сәйкес жоғары және төмен бағытталған (44-сурет) .
Жанаманың α еңкею бұрышы x нүктесі арқылы бірмәнді анықталатындықтан,
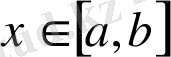 нүктелері үшін
нүктелері үшін
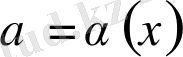 - мәндері
- мәндері
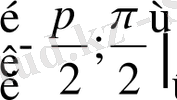 аралығында жататын
бұрыштық функция
.
аралығында жататын
бұрыштық функция
.
Кез келген
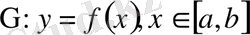 қисығы үшін [a, b] кесіндінің кейбір нүктелерінде бұрыштық функция болмауы да мүмкін. Өйткені, анықтама бойынша, Г қисығының
қисығы үшін [a, b] кесіндінің кейбір нүктелерінде бұрыштық функция болмауы да мүмкін. Өйткені, анықтама бойынша, Г қисығының
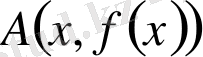 нүктесіндегі жанамасының бар болуы келесі ақырлы шектің
нүктесіндегі жанамасының бар болуы келесі ақырлы шектің
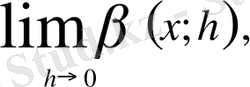
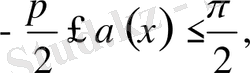
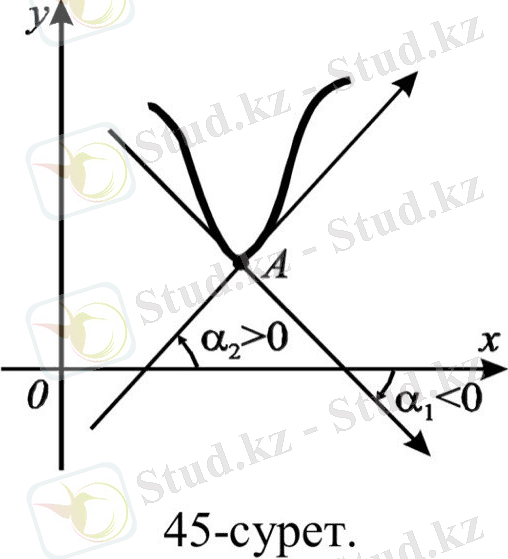
бар болуымен пара пар. Мысалы, 45-суретте көрсетілген қисықтың А нүктесінде жанамасы, демек бұрыштық функциясы жоқ (анықталмаған), өйткені
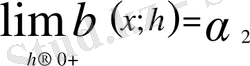
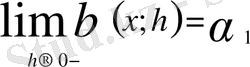
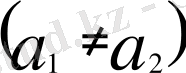
яғни,
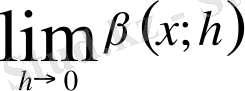
шегі жоқ. Бірақ, еңкею бұрыштары
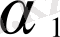 ,
,
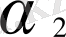 тең, сәйкес
сол жақ
және
оң жақ
жанамалары бар.
тең, сәйкес
сол жақ
және
оң жақ
жанамалары бар.
Енді (1) теңдікті пайдаланып, (теңдігін (39 және 40 суреттерді қараңыз) және arctg функциясының кез келген нүктеде үзіліссіздігін ескеріп, қисықтың берілген нүктедегі бұрыштық функциясын келесі түрде жаза аламыз
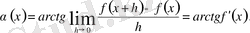
Енді (2) теңдікті пайдаланып келесі маңызды тұжырымға келеміз. Егер
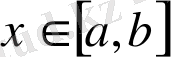 нүктесінде
нүктесінде
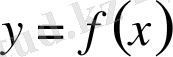 функциясының (кең мағыналы) туындысы бар болса, онда
функциясының (кең мағыналы) туындысы бар болса, онда
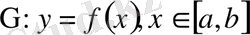 қисығының
қисығының
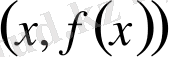 нүктесінде бұрыштық коэффициенті
нүктесінде бұрыштық коэффициенті
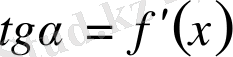 тең жанамасы бар және, керісінше, егер Γ қисығы үшін
тең жанамасы бар және, керісінше, егер Γ қисығы үшін
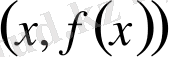 нүктеде еңкею бұрышы
нүктеде еңкею бұрышы
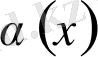 тең жанама бар болса, онда x нүктесінде кең мағыналы туынды бар
тең жанама бар болса, онда x нүктесінде кең мағыналы туынды бар
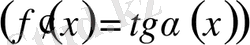 . Қысқаша айтқанда, кең мағыналы туындының бар болуы мен жанаманың бар болуы - парапар ұғымдар.
. Қысқаша айтқанда, кең мағыналы туындының бар болуы мен жанаманың бар болуы - парапар ұғымдар.
Мұндай тұжырым ақырлы туынды үшін орындалмайды!
Анықтама.
Егер берілген
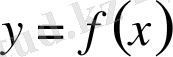
 функциясы үшін ∆ аралығының әрбір нүктесінде (2) теңдікпен анықталатын
функциясы үшін ∆ аралығының әрбір нүктесінде (2) теңдікпен анықталатын
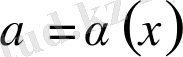 функция бар болса, онда ол f функциясының ∆ аралығындағы бұрыштық функциясы деп аталады.
функция бар болса, онда ол f функциясының ∆ аралығындағы бұрыштық функциясы деп аталады.
Анықтама
.
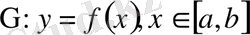 қисығы берілсін. Егер f функциясының [a; b] кесіндіде
үзіліссіз бұрыштық функциясы
бар болса, онда Γ - осы кесіндіде тегіс қисық деп аталады.
қисығы берілсін. Егер f функциясының [a; b] кесіндіде
үзіліссіз бұрыштық функциясы
бар болса, онда Γ - осы кесіндіде тегіс қисық деп аталады.
Мысал . Келесі функциялармен берілген қисықтар тегіс пе:
а)
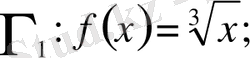
б)
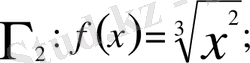
с)
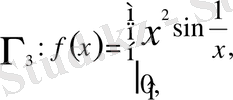
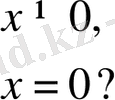
а)
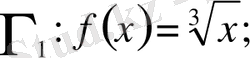 қисығының бұрыштық функциясы бар және ол кез келген нүктеде үзіліссіз. Шынында да,
қисығының бұрыштық функциясы бар және ол кез келген нүктеде үзіліссіз. Шынында да,
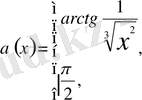
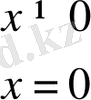
және
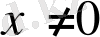 нүктелерінде екі үзіліссіз функцияның композициясы да үзіліссіз, ал x = 0 нүктесінде
нүктелерінде екі үзіліссіз функцияның композициясы да үзіліссіз, ал x = 0 нүктесінде
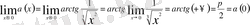
теңдігі орындалатындықтан α(x) кез келген нүктеде үзіліссіз функция, демек
 - тегіс қисық;
- тегіс қисық;
b) Егер x ≠ 0 болса, онда (2) теңдік бойынша
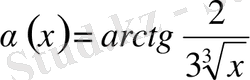
Ал x = 0 нүктесі үшін келесі теңдіктер орындалады:
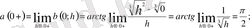
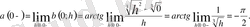
Мұнда
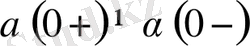 болғандықтан (2) шек жоқ, яғни x =0 нүктесінде бұрыштық функция (жанама) анықталмаған. Олай болса,
болғандықтан (2) шек жоқ, яғни x =0 нүктесінде бұрыштық функция (жанама) анықталмаған. Олай болса,
 - тегіс емес қисық;
- тегіс емес қисық;
c) Бұл функция үшін кез келген нүктеде бұрыштық функция бар:
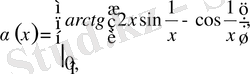
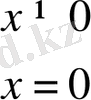
Бірақ, ол x = 0 нүктесінде үзілісті: x = 0 - бұрыштық функцияның екінші текті үзіліс нүктесі (
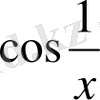 функциясының x = 0 нүктеде шегі жоқ) . Анықтама шарты орындалмағандықтан,
функциясының x = 0 нүктеде шегі жоқ) . Анықтама шарты орындалмағандықтан,
 тегіс емес қисық. «Тегіс функция» ұғымының белгілі анықтамасы келесі түрде тұжырымдалады.
тегіс емес қисық. «Тегіс функция» ұғымының белгілі анықтамасы келесі түрде тұжырымдалады.
Анықтама.
Егер
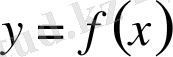 үзіліссіз функциясының туындысы [a, b] кесіндісінде үзіліссіз болса, онда функция осы кесіндіде тегіс деп аталады. Бұл анықтама бойынша,
үзіліссіз функциясының туындысы [a, b] кесіндісінде үзіліссіз болса, онда функция осы кесіндіде тегіс деп аталады. Бұл анықтама бойынша,
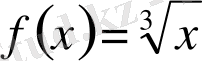 функциясы тегіс емес (тексеріңіз) . Біз жоғарыда
функциясы тегіс емес (тексеріңіз) . Біз жоғарыда
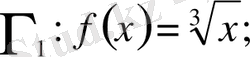
қисығының тегіс екенін көрсеткенбіз.
Ендеше
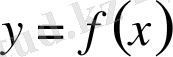 функциясының тегіс болуы мен
функциясының тегіс болуы мен
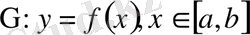 қисығының тегіс болуы пара пар ұғымдар емес.
қисығының тегіс болуы пара пар ұғымдар емес.
2. 1. Элементар функцияның туындысын анықтама арқылы
есептеу
Кейбір элементар функциялар үшін олардың туындыларын анықтама арқылы есептеу жолын көрсетейік.
1) Егер
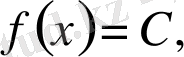
 - тұрақты сан болса,
- тұрақты сан болса,
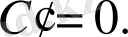
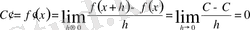
2) Көрсеткіштік функция
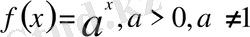 үшін
үшін
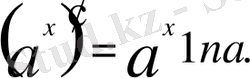
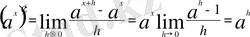
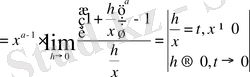
3) Дәрежелік функция
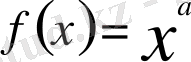 ( а- сан) үшін
( а- сан) үшін
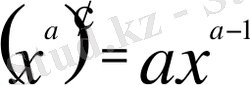
Дербес жағдайда, егер
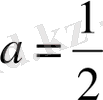 немесе a = −1 болса, онда
немесе a = −1 болса, онда
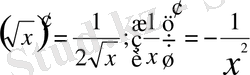
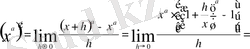
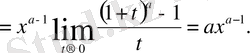
4) Логарифмдік функция
:
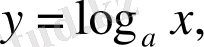 a ≠ 1. a үшін
a ≠ 1. a үшін
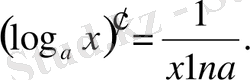
Дербес жағдайда, егер a=e болса, онда
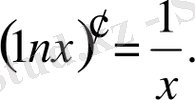
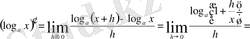
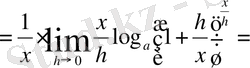
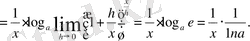
5.
Тригонометриялық функциялар
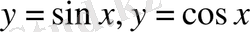 үшін
үшін
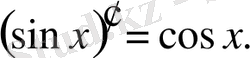
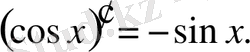
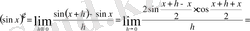
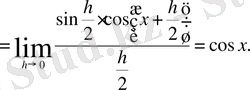
(7) формула да осы сияқты дәлелденеді.
Қорытынды
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz