Монотонды функциялардың қасиеттері, біржақты туындылары және абсолют үздіксіздік


Монотонды функциялар
Алдымен кейбір терминдерді тыянақтап алайық.
[а, b], [а, b), (а, b], (а, b) жиындарын ортақ атпен аралық деп атпн. <а, b> таңбасымен белгілейміз. Сондай-ақ, мына терминдердің де мағынасын тыянақтап алайық:
<а, b>
аралығында жатқан кезкелген
 нүктелері үшін
нүктелері үшін
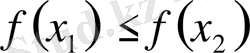 болса, онда осы аралықта
болса, онда осы аралықта
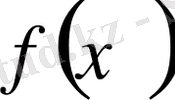 функциясы өспелі функция деп, ал
функциясы өспелі функция деп, ал
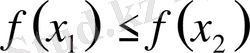 болса, онда
болса, онда
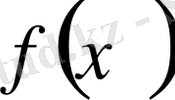 осы аралықта кемімелі функция деп айтатын боламыз.
осы аралықта кемімелі функция деп айтатын боламыз.
Егер осы жағдайда
 (немесе
(немесе
 ) теңсіздігі орындалса, онда
) теңсіздігі орындалса, онда
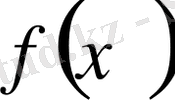 функциясы
<а, b>
аралығында шынайы өспелі (шынайы кемімелі) функция деп айтатын боламыз.
функциясы
<а, b>
аралығында шынайы өспелі (шынайы кемімелі) функция деп айтатын боламыз.
Өспелі, не кемімелі функция жалпы атпен монотонды функция деп аталады.
Монотонды функцияның таңбасын өзгертсе, оның өзгеру бағыты керіге ауысатындығы (мысалы,
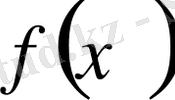 өспелі болса, онда
өспелі болса, онда
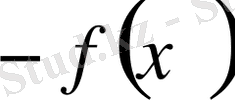 кемімелі болатындығы) түсінікті. Сондықтан, ілгеріде монотонды функцияларды зерттегенде тек өспелі функцияларды қарастырса жеткілікті.
кемімелі болатындығы) түсінікті. Сондықтан, ілгеріде монотонды функцияларды зерттегенде тек өспелі функцияларды қарастырса жеткілікті.
Монотонды функцияларға тән бірқатар қасиетгерге тоқталайық.
1-қасиет. Егер [а, b] кесіндісінің әрбір нүктесінде
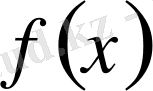 - ақырлы және осы кесіндіде өспелі болса, онда ол осы кесіндіде шенелген функция.
- ақырлы және осы кесіндіде өспелі болса, онда ол осы кесіндіде шенелген функция.
Шынында да, кезкелген
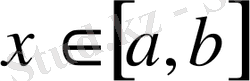 үшін
үшін
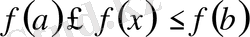 .
.
(Егер
 -
кемімелі функция болса, онда
-
кемімелі функция болса, онда
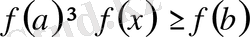 екендігі де айқын) .
екендігі де айқын) .
2-қасиет. Кесіндіде мәндері ақырлы монотонды функцияның тек қана бірінші текті үзіліс нүктелері болуы мүмкін және үзіліс нүктелері ақырлы не саналымда жиын құрайды.
Дәлелдеуі.
Егер
[а, b]
кесіндісінде
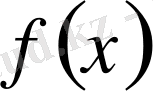 функциясы монотонды өспелі (функция болса, онда әрбір
функциясы монотонды өспелі (функция болса, онда әрбір
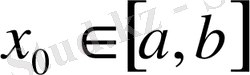 және
және
 үшін
2
үшін
2
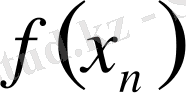 өспелі және жоғарыдан шенелген тізбек. Сондықтан
өспелі және жоғарыдан шенелген тізбек. Сондықтан
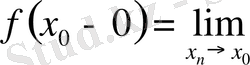
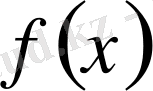 бар, яғни
х
0
нүктесінде
бар, яғни
х
0
нүктесінде
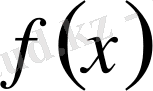 функциясының солжақты шегі
функциясының солжақты шегі
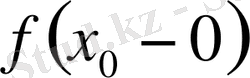 анықталған. Осыған ұқсас,
анықталған. Осыған ұқсас,
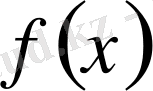 функциясының
х
0
нүктесіндегі оңжақты шегі
функциясының
х
0
нүктесіндегі оңжақты шегі
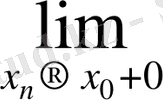
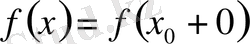 де бар. Ал
де бар. Ал
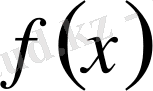 функцияның
х
0
нүктесіндегі мәні болса, онда,
функцияның
х
0
нүктесіндегі мәні болса, онда,
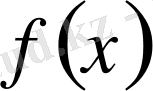 монотонды өспелі болғандықтан,
монотонды өспелі болғандықтан,
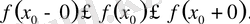 (1) (Егер
(1) (Егер
 не
не
 болса, онда (1) теңсіздіктерінің гек екіншісі, ие сәйкес біріншісі ғана мағыналы болады), Осы теңсіздіктердегі үш сан өзара тең болса, онда
болса, онда (1) теңсіздіктерінің гек екіншісі, ие сәйкес біріншісі ғана мағыналы болады), Осы теңсіздіктердегі үш сан өзара тең болса, онда
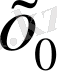 нүктесінде
нүктесінде
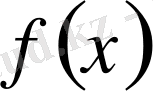 функциясы үздіксіз функция. Демек, басқа жағдайда
функциясы үздіксіз функция. Демек, басқа жағдайда
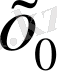 бірінші текті үзіліс нүктесі. Теңсіздік (1) нақты жағдайда мына түрлердін бірінде болуы мүмкін
бірінші текті үзіліс нүктесі. Теңсіздік (1) нақты жағдайда мына түрлердін бірінде болуы мүмкін
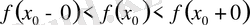 (а)
(а)
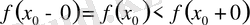 (б)
(б)
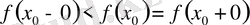 (в)
(в)
(а) жағдайында
х
0
нүктесінде
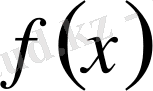 функциясы алдымен
функциясы алдымен
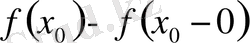 санына, сонан кейін бірден
санына, сонан кейін бірден
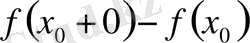 санына "секіріп" өседі (1-сурет) .
санына "секіріп" өседі (1-сурет) .
Сонымен а) жағдайында
х
0
нүктесінде функцияның жалпы өзгеруі
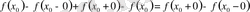
санына тең. Осыған ұқсас, (б), (в) жағдайларында да функцияпық х 0 нүктесіндегі өзгеруі
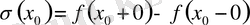 (1)
(1)
санына тең. Осы санды
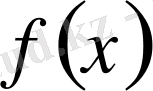 функциясының
х
0
нүктесіндегі секірісі деп атаймыз.
функциясының
х
0
нүктесіндегі секірісі деп атаймыз.
Әрбір үзіліс нүктесі
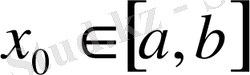 және
және
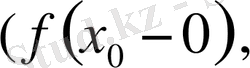
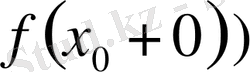 интервалы арасында бірмәнді сәйкестік бар.
интервалы арасында бірмәнді сәйкестік бар.
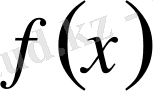 монотонды өспелі функция болғандықтан кезкелген
монотонды өспелі функция болғандықтан кезкелген
 үзіліс нүктелеріне сәйкес интервалдар
үзіліс нүктелеріне сәйкес интервалдар
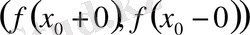 және
және
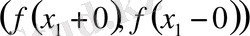
қиылыспайды, себебі,
 болғандықтан
болғандықтан
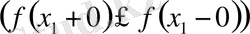 . Ал, 1- қасиет бойынша
. Ал, 1- қасиет бойынша
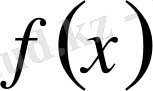 функциясының мәндері түгел
функциясының мәндері түгел
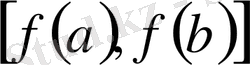 кесіндісінде жатқандықтан, осы интервалдар да
кесіндісінде жатқандықтан, осы интервалдар да
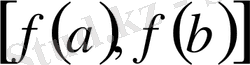 кесіндісіндс жатады, демек олар, ең көп дегенде, саналымды жиын құрайды.
кесіндісіндс жатады, демек олар, ең көп дегенде, саналымды жиын құрайды.
Салдар. Кесіндіде монотонды функция осы кесіндінің барлық нүктелерде дерлік үзіліссіз болады.
Келесі қарастырылатын мәселе - монотонды функциянық туындысы барлық нүктелерде дерлік бар болуы.
Осыған байланысты, қайсы бір
х
0
нүктесінің маңайында анықталған
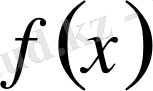 функциясының осы нүктедегі туындылық сандарының анықтамасын берейік. Олар төмендегі теңдіктермен анықталады:
функциясының осы нүктедегі туындылық сандарының анықтамасын берейік. Олар төмендегі теңдіктермен анықталады:
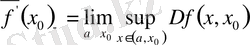 (2)
(2)
 (3)
(3)
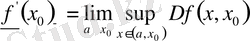 (4)
(4)
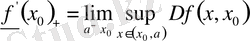 (5)
(5)
Мұндағы
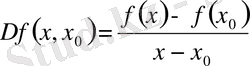
Бұл (2) -(5) шектерінің мәні - ақырлы, не ақырсыз - әрқашан бар болады.
Осы тұжырымды дәлелдейік. (2) - (5) теңдіктің біреуі үшін, мысалға (2) теңдігі үшін дәлелдесек болды. Қалғандары ұқсас жолмен дәлелденеді. Егер
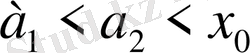 болса, онда
болса, онда
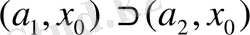 екені айқын.
екені айқын.
Осыдан,
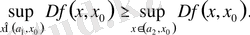
демек,
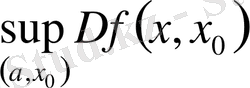 кезінде а-ға тәуелді кемшелі функция, сондықтан оның шегі
кезінде а-ға тәуелді кемшелі функция, сондықтан оның шегі
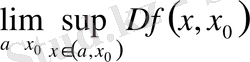
бар (ақырлы не ақырсыз) .
Осы (2) -(5) теңдіктерімен анықталған төрт сан жазылу ретіне сәйкес солжақты жоғарғы туындылық сан, оңжақты жоғарғы туындылық сан, солжақты төменгі туындылық сан, оңжақты төменгі туындылық сан деп аталады.
Мысал ретінде
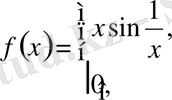
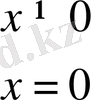
функциясын қарастырайық. Бұл функция х = 0 нүктесінде үзіліссіз, бірақ туындысы жоқ. Сөйтсе де, осы нүктеде туындылық сандарының төртеуі де ақырлы, атап айтқанда,
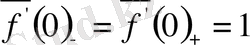 (6)
(6)
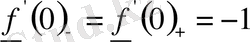 (7)
(7)
болатынын дәлелдеу қиын емес.
Екінші мысал ретінде
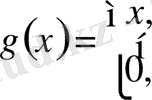
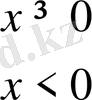
функциясын қарастырып,
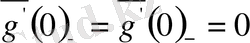
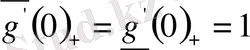
екенін көреміз.
Сонымен, осы мысалдарда қарастырылған
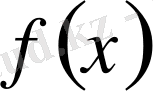 функциясының оңжақты және солжақты жоғарғы туындылық сандары тең, сондай-ақ, төменгі туындылық сандары да өзара тең болды. Ал
функциясының оңжақты және солжақты жоғарғы туындылық сандары тең, сондай-ақ, төменгі туындылық сандары да өзара тең болды. Ал
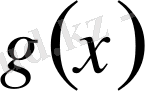 функциясының біржақты жоғарғы және төменгі туындылық сандары өзара тең. Егер
функциясының біржақты жоғарғы және төменгі туындылық сандары өзара тең. Егер
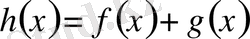
болса, онда
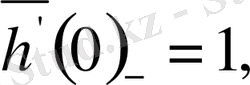
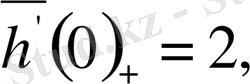
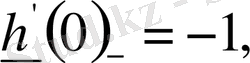
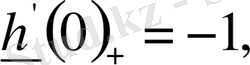 яғни
яғни
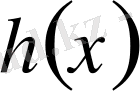
функциясының х = 0 нүктесіндегі туындылық сандары әртүрлі екенін көреміз.
Анықтама.
Егер
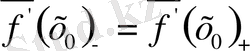 болса, онда олардың ортщ мэнін
болса, онда олардың ортщ мэнін
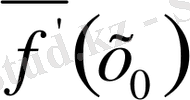 арқылы белгілейміз де, оны
арқылы белгілейміз де, оны
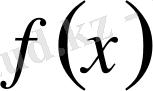 функциясының х
0
нүктесіндегі жоғарғы туындысы деп атаймыз.
функциясының х
0
нүктесіндегі жоғарғы туындысы деп атаймыз.
Осыған ұқсас,
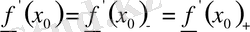
санын
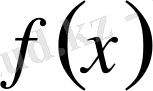 функциясының
функциясының
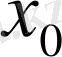 нүктесіндегі төменгі туындысы
деп атаймыз.
нүктесіндегі төменгі туындысы
деп атаймыз.
Жоғарыдағы бірінші мысалда
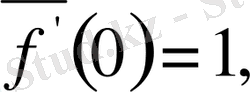
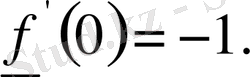 Туындылық сандардың кейбір қарапайым қасиетгерін атап өтейік.
Туындылық сандардың кейбір қарапайым қасиетгерін атап өтейік.
1. Егер
 функциясы х
0
нүктесінің маңайында өспелі болса, онда
функциясы х
0
нүктесінің маңайында өспелі болса, онда
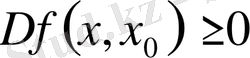 екені айқын, демек туындылық сандардың бәрі де бұл нүктеде теріс емес. Осыдан, бұл жағдайда
екені айқын, демек туындылық сандардың бәрі де бұл нүктеде теріс емес. Осыдан, бұл жағдайда
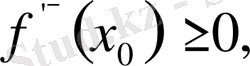
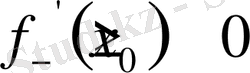 (10)
(10)
теңсіздіктері шығады.
2. Егер
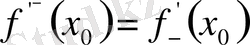 болса, онда х
0
нүктесінде
болса, онда х
0
нүктесінде
 функциясының туындысы бар және
функциясының туындысы бар және
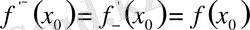 .
.
Басқаша айтқанда, жоғарғы
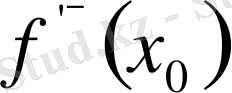 және төменгі
және төменгі
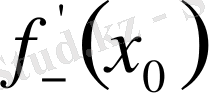 іуындылардың х
0
нүктесінде өзара тең болуы осы нүктеде
іуындылардың х
0
нүктесінде өзара тең болуы осы нүктеде
 туындысының болуының қажет және жеткілікті шарты.
туындысының болуының қажет және жеткілікті шарты.
Дәлелдеуі.
Анықтама бойынша
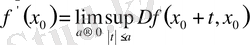 Супремумның анықтамасы бойынша а > 0 үшін
Супремумның анықтамасы бойынша а > 0 үшін
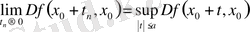 болатындай
{t
п
}
тізбегі табылады.
болатындай
{t
п
}
тізбегі табылады.
Сондықтан
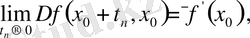
демек, егер
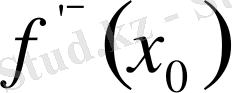 бар болса, онда кезкелген
бар болса, онда кезкелген
 тізбегі үшін, оның ішінде
тізбегі үшін, оның ішінде
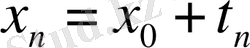 тізбегі үшін,
тізбегі үшін,
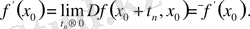 Ұқсас жолмен
Ұқсас жолмен
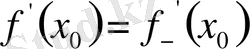 екендігі дәлелденеді, демек,
екендігі дәлелденеді, демек,
Керісінше, егер
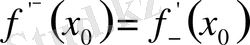 болса, онда
болса, онда
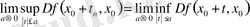
Функцияның нүктедегі жоғарғы және төменгі шектерінің тең болуы бұл функцияның осы нүктеде шегі бар екендігіне пара-пар болатыны анализден белгілі. Сондықтан (11) теңдіктен
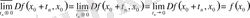
яғни жоғарғы және төменгі туындылары бар нүктеде функцияиым туындысы бар. Мақсатымыз осыны дәлелдеу еді.
1-лемма
.
Функция
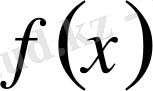 [а, b]
кесіндісінде шынайы өсетін болсын, Егер жиын
Е
[а, b]
кесіндісінде шынайы өсетін болсын, Егер жиын
Е
 (а, b)
мен
р
0
> 0
саны үшін
(а, b)
мен
р
0
> 0
саны үшін
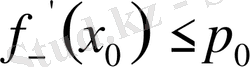 теңсіздігі әрбір
х
теңсіздігі әрбір
х
 Е
үшін орындалатын болса, онда
Е
үшін орындалатын болса, онда
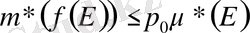
Дәлелдеуі.
Кезкелген р
0
> 0 және
 сандарын алайық! 11 пункттегі 1-теорема бойынша
сандарын алайық! 11 пункттегі 1-теорема бойынша
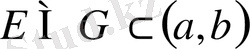 және
және
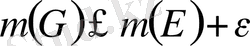 шарттары орындалатындай
шарттары орындалатындай
 жиыны табылады. Лемманың шарты бойынша кезкелген
жиыны табылады. Лемманың шарты бойынша кезкелген
 үшін
үшін
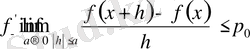 (12)
(12)
демек,
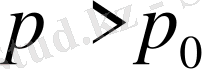 болғандықтан
болғандықтан
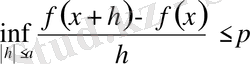 (13)
(13)
болатындай а > 0 табылады.
 ашық жиын және
ашық жиын және
 болғандықтан, а санын жеткілікті аз етіп алсақ, онда
болғандықтан, а санын жеткілікті аз етіп алсақ, онда
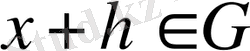 . Енді
. Енді
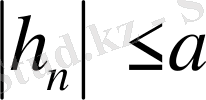 және
және
 талаптарына сай {
һ
п
}тізбегін алайық. Әрине
һ
п
= һ
п
(х)
әрбір
талаптарына сай {
һ
п
}тізбегін алайық. Әрине
һ
п
= һ
п
(х)
әрбір
 Е үшін өзінше тізбек. Төменгі туынды бар дегеніміз
Е үшін өзінше тізбек. Төменгі туынды бар дегеніміз
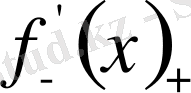 және
және
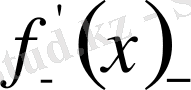 сандары бар және екеуі тең деген сөз. Сондықтан
һ
п
> 0
деп алсақ та шек (12) төменгі туындыға тең болады. Сонымен
һ
п
> 0
деп жорып, мына кесінділерді қарастырайық:
сандары бар және екеуі тең деген сөз. Сондықтан
һ
п
> 0
деп алсақ та шек (12) төменгі туындыға тең болады. Сонымен
һ
п
> 0
деп жорып, мына кесінділерді қарастырайық:
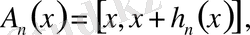
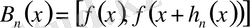 (14)
(14)
Мұнда
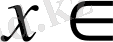 Е және
Е және
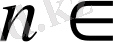 N.
N.
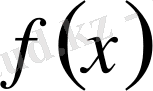 функциясы шынайы өсетін және
һ
п
> 0,
болғандықтан,
функциясы шынайы өсетін және
һ
п
> 0,
болғандықтан,
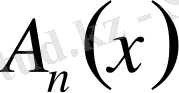
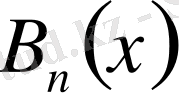 кесінділерінің ешқайсысы нүктеге айналмайды (басқаша айтқанда олар мардымды кесінділер) .
кесінділерінің ешқайсысы нүктеге айналмайды (басқаша айтқанда олар мардымды кесінділер) .
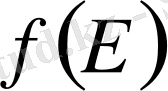 арқылы
арқылы
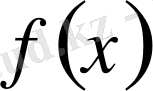 функциясының Е жиынында қабылдайтын мәндерінің жиынын
:
белгілейміз. Көрер көзге, әрбір
функциясының Е жиынында қабылдайтын мәндерінің жиынын
:
белгілейміз. Көрер көзге, әрбір
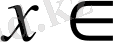 Е үшін
Е үшін
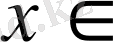 А
п
(х)
және
А
п
(х)
және
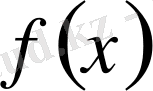
 В
п
(х),
демек
В
п
(х),
демек
В = { В
п
(х) },
яғни
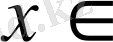 Е,
Е,
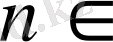 N шарттарына сәйкес барлық кесінділер жиыны
N шарттарына сәйкес барлық кесінділер жиыны
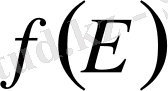 жиынын Витали мағынасында бүркейді. Витали теоремасы бойынша В жиынында өзара қиылыспайтын, ақырлы не саналымды және
жиынын Витали мағынасында бүркейді. Витали теоремасы бойынша В жиынында өзара қиылыспайтын, ақырлы не саналымды және
 шарты орындалатын
шарты орындалатын
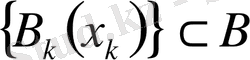 ішжиыны бар. Осы
В
к
(х
к
)
кесінділеріне сәйкес
А
к
(х
к
)
кесінділері де өзара қиылыспайтыны айқын. Сондықтан (кесіндінің өлшемі оның ұзындығына тең екенін ескере),
ішжиыны бар. Осы
В
к
(х
к
)
кесінділеріне сәйкес
А
к
(х
к
)
кесінділері де өзара қиылыспайтыны айқын. Сондықтан (кесіндінің өлшемі оның ұзындығына тең екенін ескере),
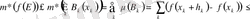
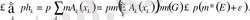
Енді
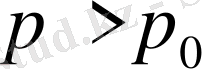 және
және
 шарттарына сай р мен
шарттарына сай р мен
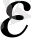 кезкелген сандар болғандықтан,
кезкелген сандар болғандықтан,
 және
және
 кезінде соңғы теңсіздіктен
кезінде соңғы теңсіздіктен
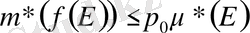
теңсіздігі шығады. Лемма дәлелденді.
2-лемма
. Егер
[а, b]
кесіндісінде
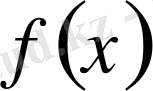 шынайы өсетін болса,
шынайы өсетін болса,
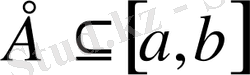 жиынының әрбір нүктесінде
жиынының әрбір нүктесінде
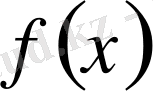 үз
іліссіз және
үз
іліссіз және
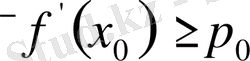 болса, онда
болса, онда
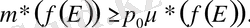
Дәлелдеуі.
Кезкелген
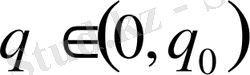 және
және
 сандарын алайық.
сандарын алайық.
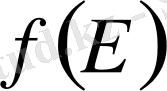 жиыны үшін
жиыны үшін
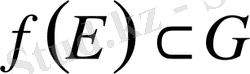 және
және
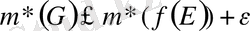 шарттарына сай ашық жиын
шарттарына сай ашық жиын
 табылады. Шарт бойышпа әрбір
табылады. Шарт бойышпа әрбір
 үшін
үшін
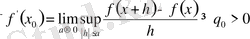
болғандықтақ,
 шартына сай
шартына сай
 саны үшін
саны үшін
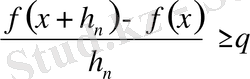
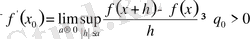
теңсіздігі,
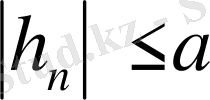 жә
жә
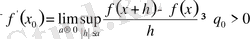 не
не
 шарттарын қанағаттандыратын қайсыбір
шарттарын қанағаттандыратын қайсыбір
 тізбегі үшін, орындалады. 1-леммадағы қорытуға үдсае, бул жолы да һ„ > 0 деп есептеуге болады.
тізбегі үшін, орындалады. 1-леммадағы қорытуға үдсае, бул жолы да һ„ > 0 деп есептеуге болады.
Тағы да А п (х) = [х, х+һ„(х) ], В п (х) = [і"(х) Дх + һ„(х) ) ] кесінділеріп қарастырайық. Ашық жиын О Г(х) функциясының Е жиынында қабылдайтын мэвдерінің Г(Е) жиынын қамтңды. Оған қоса, Г(х) осы жиынында үзіліссіз болғандыктан, һ„ мейлінше аз болса В„(х) с О.
А„(х) кесінділері Е жиынын Витали мағынасында буркейтіні айқық, (11-п., 6-теорема) (һ п (х) } бүркемесінен саиы ақырлы, болмаса саналымды және и*(Е\^А к (х к ) ) = 0 шартыи қанағатгандыратын {А к (х к ) }ь £ ы қиылыспайтын кесінділердің жиыныи бөліп алуға болады. Осы кесінділерге сэйкес В к (х к ) кесінділері де, Г(х) шынайы өспелі болғандықтан, өзара қиылыспайды. Сондыктан, жиыи өлшемінің қасиетгерін ескере отырып, мына теңсіздіктерге келеміз:
* 4=1 Ы\
Ч 4=1
= - £ мВ к (Хк) = -м(иВ К (х К ) ) < -цО < - [\і*(т + е]
Мүлдағы я < Чо және 8 > 0 сандары осы теңсіздіктерді қанағатгыратын кезкелген сандар болғандықтан ц Т ^ 0 және 8 -> 0 кезде, осыдан : '1
114
II ц*(Ғ(Е) ) ^ЧоЦ*(Е)
; і еңсіздігі шығады. Лемма дэлелденді.
Теорема. Егер/(х) функциясы [а, Ь] кесіндісінде өспелі болса, онда (а, в) интервалының барлың нүктелерінде дерлік оның туындысы бар және ол (а, в) интервалында цосындыланатын функция. Сонымен қатар 3
\Г(х) <ііі<№-№ (и)
Дәлелдеуі. §(х) = {(х) + х функциясы шынайы өспелі ф^кция. Осы () ункцияның үзіліссіз нүктелерінің жиыны Е болса, онда [а, Ь] \ Е ақырлы не саналымды жиын. Функцияның туындысы ақырсыз болатын Ііоо = {хеЕ: / (х) = <я} жиынының өлшемі нөлге тең, себебі, егер ; ^і^Еос = а > 0 болса, онда 2-леммадағы ц 0 < / (*) = оо санын мейлінше і улкен етіп алуға болар еді. Сонда лемманың тү_жырьшы бойынша ц*(§(Еоо) > роа мейлінше үлкен сан болар еді, бірақ ол мүмкін емес. ! Демек, ц*Еоо = 0, яғни Е да өлшемді жиын және \лЕ х = 0. Енді кезкелген 0<р<^ рационал сандары үшін
Е рч = {хеЕ: 2_'(х) < р < Ч < ^'(х) } жиывдарын анықтайық. 1-2- леммалар бойынша
Ч м*(Е м ) < ц*(§(Ер Ч ) ) < р ц*(Еи), Ал, бүл теңсіздіктер тек ц*(Е р( , ) = 0 болғанда ғана орындала алады.
Егер х нүктесінде §'(х) жоқ болса, онда & '(■*) * ё'(х), ал функция £(х) өспелі болғандықтан 0 < §'( х ) < ё'( х) - Бүл жағдайда
£'0) <р<ч< §'(х)
теңсіздіктері орындалатындай оң рационал сандар р мен ^ табыладм демек, х е Е рч . Сондықтан мұндай х нүктелерінің жиыны А = д у^ I',, ,,
жиынына, яғни өлшемі нөлге тең жиындардың саналымды бірігуіи енеді.
Сонымен, §(х) функциясының туындысы жоқ нүктелер (а, в) \Е, Е^ және А жиындарының бірігуіне енеді, ал бұлар өлшемі нөлге тсм жиындар. Демек, §(х) функциясы (а, в) интервалының барлмк нүктелерінде дерлік туывдалатын функция. Ал Г(х) = §(х) - х болғандықтан, (а, в) интервалыньщ барлық нүктелерінде дерлік §(х) функциясының туындысы бар.
Енді (15) теңдігін дэлелдеу қалды. Сол мақсатпен §(х) функциясыіі х < а үшін Г(х) = Г(а) және х > Ь үшін £(х) = Ғ(Ь) тевдіктерімен [а, һ кесіндісінің сыртына жалғастырайық. Сонансоң, хе[а, Ь] нүктелеріндс
Ғ в (х) = п [Г(х + 1/п) - Қх) і (пеМ)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz