Модуль таңбасы бар теңсіздіктерді шешу әдістері


Модульді теңсіздіктерді шешу әдістері
Теңдулермен қатар теңсіздіктер де қазіргі математика салаларында маңызды орын алады. Көптеген зерттеу жұмыстарында теңсіздіктерді қолданады және көп жағдайларда бұл жұмыстардың нәтижелері де теңсіздіктермен көрсетіледі.
Теңдеулер сияқты, математика курсында оқылатын теңсіздіктердің де бірнеше түрлері бар: бүтін теңсіздіктер, рационал теңсіздіктер, иррационал теңсіздіктер, модуль таңбасы бар теңсіздіктер, тригонометриялық теңсіздіктер, көрсеткіштік және логарифмдік теңсіздіктер.
Модуль таңбасы бар теңсіздіктер
Айнамалылары модуль таңбасының астында кездесетін теңсіздіктерді модуль таңбасы бар теңсіздіктер деп атаймыз.
Модуль таңбасы бар теңсіздіктерді шешідің бірнеше әдістері бар:
- модульді сан осіндегі екі нүктенің ара қашықтығы ретінде қарастырып, теңсіздікті шешу.
- мысал. теңсіздігін щещу керек.
Шешуі.
- ді сан осіндегі
және 1 нүктелерінің ара қашықтығы деп қарастырамыз. Теңсіздіктің шарты бойынша біз сан осіндегі 1 нүктесінен 3 бірліктен кіші қашықтықта жатқан нүктелердің бәрін табуымыз керек. Сан осінде 1 нүктесін және одан үш бірлік өлшем қашықтықта жататын екі нүкте - береуі 1 нүктесінің оң жағында, екіншісі оның сол жағында болатындай етіліп салынады. Сан өсінде салынған нүктелер - 2, 1, 4.
Сөйтіп, теңсіздіктің жауабы (-2; 4) .
Бұл әдіс кез келген модуль таңбасы бар теңсіздікті шешуге жарамайды. Бұл әдіспен тек қана 1 - мысалдағы теңсіздік сияқты теңсіздіктерді шешуге болады.
- Теңсіздіктердің екі жағын квадраттау әдісі.
теңсіздігін шешу керек дейік.
және
- тың анықталу облысындажататын
-тің кезкелген мәнінде
, болатыны түсінікті. Сондықтан
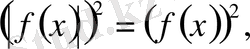
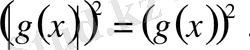
Берілген теңсіздік мына.
(2) теңсіздігіне барабар. Сөйтіп (1) теңсіздігін (2) теңсіздігін шешуге келтіреді.
2-мысал .
теңсіздігін шешу керек.
Шешуі. Берілген теңсіздіктің екі жағы да теріс
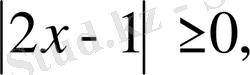
сондықтан берілген теңсіздікті өзімен барабар мына теңсіздікпен алмастырамыз:
.
Осыдан
немесе
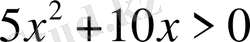
Осыдан екі жүйе пайда болады. Берілген теңсіздіктің шешуі осы екі жүйенің шешулерінің бірігуі болғандықтан былай жазамыз:
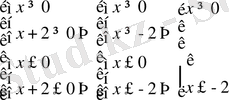
және
жүйе құрамайды. Бұлар екі жүйенің шешулері. Олардың бірігуі берілген теңсіздіктің жауабы болады.
Жауабы:
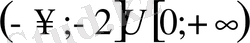
3-мысал.
теңсіздігін шешейік.
Шешуі. Теңсіздіктің екі жағы да теріс емес, ендеше теңсіздіктің екі жағын квадраттаймыз, содан
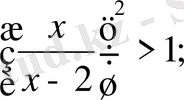
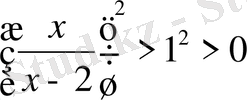
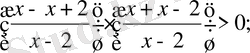
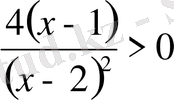
мұндағы
яғни бөлшектің бөлімі нөл болмауы керек.
- тің қабылдай алатын мәндерінің облысы

Ақырғы теңсіздіктен
. Теңсіздіктің жауабы:
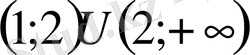
- Модульдің анықтамасына негізделген әдіс - теңсіздікті теңсіздіктер жүйесімен алмастыру.
Модельдің анықтамасы бойынша:
егер
егер
Мысал келтіріп түсіндірейік.
4-мысал.
теңсіздігін шешейік.
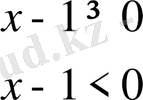
егер
егер
ендеше беріліген теңсіздікті онымен барабар екі жүйемен алмастарымыз. Берілген теңсіздіктің шешімі осы екі жүйеніңшешімдерінің бірігуі болады.
бірінші жүйенің шешуі
екінші жүйенің шешуі
Берілген теңсіздіктің шешуі осы екеуінің бірігуі. Жауабы: (-1; 3)
5-мысал
теңсіздігін шешейік.
Шешуі. Теңсіздікті мына теңсіздіктер жүйесімен алмастырайық.
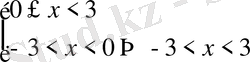
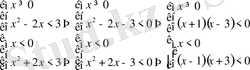
Теңсіздіктің жауабы: (-3; 3)
6- мысал .
теңсіздігін шешейік.
Шешуі. Берілген теңсіздікті шешудің орнына, мына төмендегі екі жүйені шешіп, екеуінің жауабын біріктіріп, берілген теңсіздіктің жауабы етіп аламыз.
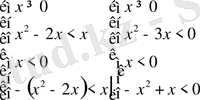
Осыдан шығатыны;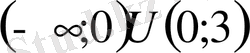
Теңсіздіктің жауабы осы.
7- мысал.
теңсіздігін шешейік.
Шешуі. Берілген теңсіздікті екі жүйемен алмастырамыз.
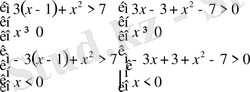
Осыдан
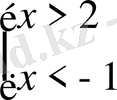
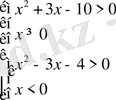
Теңсіздіктің шешуі:
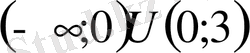
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz