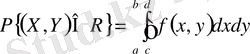Көпөлшемді ықтималдар теориясы: үлестіру функциялары, шартты үлестірімдер, тәуелсіздік, ковариация және қосындының үлестірімдері


Лекция 1
Ықтималдар теориясы,
математикалық статистика немесе кездейсоқ процесс.
Ықтималдар теьриясының қолданылуларында тәжірибе нәтижесі бір ғана кездейсоқ шамадан тәуелді емес, екі немесе одан да көп жүйе және кездейсоқ вектор құрайтын есептер кездеседі.
Мысалы кездейсоқ таңдалған жанұяның жиыны оның тамағына, киім, аяқ киім, жол шығыны, басқа да қажеттіліктеріне, өнімнің жақсы болуы ауа райына байланысты және т. б.
Кездейсоқ вектор немесе
п
-өлшемді кездейсоқ шама деп
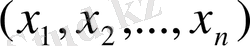 п
кездейсоқ шамадан тұратын реттелген жиынның көп өлшемді кездейсоқ шама, кездейсоқ вектор, кездейсоқ шамалар жүйесі - бір математикалық объекттің бірнеше баламасы. Көп өлшемді кездейсоқ шамалар бір өлшемді тәріздес дискретті болуымен бірге үзіліссіз болуы мүмкін.
п
кездейсоқ шамадан тұратын реттелген жиынның көп өлшемді кездейсоқ шама, кездейсоқ вектор, кездейсоқ шамалар жүйесі - бір математикалық объекттің бірнеше баламасы. Көп өлшемді кездейсоқ шамалар бір өлшемді тәріздес дискретті болуымен бірге үзіліссіз болуы мүмкін.
Дискретті кездейсоқ вектор - компоненті дискретті кездейсоқ шама болатын кездейсоқ вектор.
Үзіліссіз кездейсоқ вектор - компоненттері үзіліссіз кездейсоқ шама болатын кездейсоқ вектор.
Екі өлшемді кездейсоқ шаманың үлестіру функциясы.
Екі теңсіздіктің
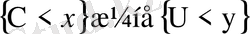 бірдей орындалу ықтималдығын (Х, У) кездейсоқ шаманың үлестіру функциясы деп атайды.
бірдей орындалу ықтималдығын (Х, У) кездейсоқ шаманың үлестіру функциясы деп атайды.
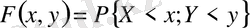
Екі өлшемді кездейсоқ шаманы декарттық координатажүйесінде кездейсоқ нүкте ретінде оң геометриялық интегралын пайдаланып,
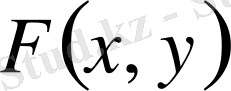 үлестіру функциясы (Х, У) кездейсоқ жүйенің төбесі (х, у) нүктесіндегі және одан төмендеу, солға қарай орналасқан шексіз квадратқа түсетін ықтималдығының бар екендігі жайында айтуға болады.
үлестіру функциясы (Х, У) кездейсоқ жүйенің төбесі (х, у) нүктесіндегі және одан төмендеу, солға қарай орналасқан шексіз квадратқа түсетін ықтималдығының бар екендігі жайында айтуға болады.
у (х, у)
0 х
Х кездейсоқ вектордың бірінші компонентасынның үлестіру функциясын
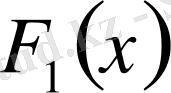 , кездейсоқ нүктенің оң жақтан х абциссасымен шектелген жартылай жазықтыққа түсу ықтималдығын белгілейміз. У шамасының үлестіру функциясын
, кездейсоқ нүктенің оң жақтан х абциссасымен шектелген жартылай жазықтыққа түсу ықтималдығын белгілейміз. У шамасының үлестіру функциясын
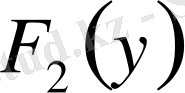 - жоғарыдан у ординатасымен шектелген жартылай жазықтыққа түсу ықтималдығын белгілейміз.
- жоғарыдан у ординатасымен шектелген жартылай жазықтыққа түсу ықтималдығын белгілейміз.
у у
у
0 х х 0 х
Екі өлшемді кездейсоқ шаманың қасиеттері:
1.
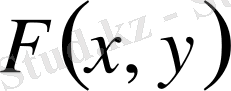 үлестіру функциясы аргументі болса кемімейтін функция:
үлестіру функциясы аргументі болса кемімейтін функция:
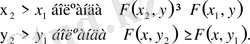
2.
 -те үлестіру функциясы нөлге тең:
-те үлестіру функциясы нөлге тең:
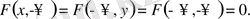
3. Егер екі аргумент те
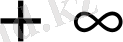 болса, онда үлестіру функциясы бірге тең:
болса, онда үлестіру функциясы бірге тең:
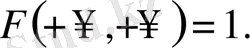
4. Егер екі аргументтің бірі
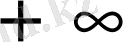 болса, екі өлшемді вектордың үлестіру функциясы компоненті басқа аргументке сәйкес болатын үлестіру функциясына ауысады:
болса, екі өлшемді вектордың үлестіру функциясы компоненті басқа аргументке сәйкес болатын үлестіру функциясына ауысады:
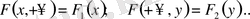
Үлестіру функциясы үзіліссіз функциялар үшін де дискретті кездейсоқ шамалар үшін де бар. Көп өлшемді үзіліссіз шамалар үлестірімі әдетте үлестірім тығыздығы сипаттайды.
Екі өлшемді кездейсоқ шаманың үлестіру тығыздығы деп кездейсоқ шаманың кішкентай тік төртбұрышқа түсу ықтималдығының осы тік төртбұрыштың ауданына қатынасының шегін айтады, оның өлшемдері нөлге ұмтылады.
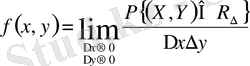
y ∆y
y
∆x
0 x x
Екі өлшемді үзіліссіз кездейсоқ шаманың үлестіру тығыздығы үлестіру функциясының екінші ретті аралас дербес туындысы ретінде есептеледі:
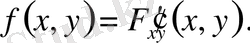
Үлестіру ықтималдығын пайдаланып (Х, У) екі өлшемді кездейсоқ шаманың a және b абсциссаларымен және c, d ординаталарымен шектелген R тік төртбұрышына түсу ықтималдығын есептеу формуласын жазуға болады:
d
R
c
a b
Үлестіру функциясын тығыздық арқылы өрнектейміз. F(x, y) үлестіру функциясы абсциссасы
 және х пен, ал ординатасы
және х пен, ал ординатасы
 және у пен шектелген тік төртбұрышқа түсу ықтималдығы болып табылады:
және у пен шектелген тік төртбұрышқа түсу ықтималдығы болып табылады:
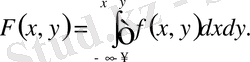
Үлестіру тығыздығының қасиеттері:
1. Екі өлшемді кездейсоқ векторлық үлестіру тығыздығы теріс емес функция
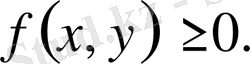
2. кі өлшемді кездейсоқ векторлық үлестіру тығыздығынан шексіз шекте алынған екі еселі интеграл 1-ге тең:
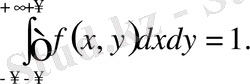
3. Кездейсоқ компоненттің үлестіру тығыздығы келесі формулалармен алынады:
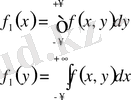
Бұл қасиет үлестіру функциясы және кездейсоқ вектордың үлестіру тығыздығымен үлестіру функциясын байланыстыратын формулалары үшін сәйкес қасиеттерден келіп шығады.
Енді дискретті екі өлшемді кездейсоқ векторларға жүгінейік.
Дискретті (Х, У) кездейсоқ вектордың үлестіру заңы - бұл (Х, У) кездейсоқ вектордың барлық мүмкін болатын мәндерінің жиыны және олардың ықтималдығы:
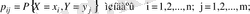
п, т- Х және У кездейсоқ шамаларының шекті және шексіз болатын мүмкін мәндер саны.
Барлық
i
және
j
мәндері бойынша
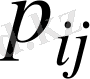 -ықтималдар қосындысы бірге тең:
-ықтималдар қосындысы бірге тең:
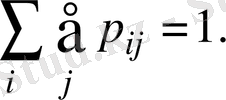
Үзіліссіз жағдай сияқты, кездейсоқ вектордың үлестіру заңын біле отырып сәйкес индекстері бойынша
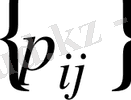 ықтималдарды қосындылау арқылы координаттар ықтималдарының үлестіруін табуға болады:
ықтималдарды қосындылау арқылы координаттар ықтималдарының үлестіруін табуға болады:
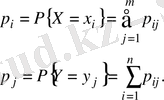
Мысалы. Өнімнің сапасы екі Х және У кездейсоқ шамаларымен сипатталады. (Х, У) кездейсоқ векторының үлестіру заңы кестеде берілген:
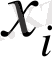
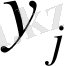
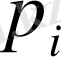
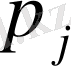
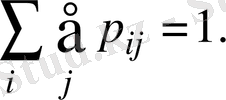
Кестенің i- ші қатары мен j- ші бағанының қиылысында ықтималдар орналасқан:
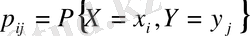
Кездейсоқ вектордың Х және У үлестіру заңының координатасын табайық.
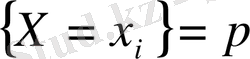 оқиғасының
i-
ші қатары орналасқан ықтималдар қосындысы болып табылады.
оқиғасының
i-
ші қатары орналасқан ықтималдар қосындысы болып табылады.
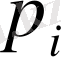 ықтималдары кестенің соңғы бағанында орналасқан.
ықтималдары кестенің соңғы бағанында орналасқан.
Х кездейсоқ шаманың үлестіру қатары келесі түрге ие:
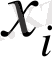
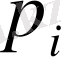
У үлестіруінің қатарын кестенің баған элементтері қосындысын анықтай отырып табамыз. Бұл
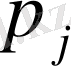 ықтималдары кестенің соңғы қатарында орналасқан.
ықтималдары кестенің соңғы қатарында орналасқан.
У кездейсоқ шаманың үлестіру қатары келесі түрге ие:
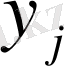
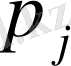
Енді п кездейсоқ шамалар немесе п -өлшемді кездейсоқ шамалар жүйесіне көшейік.
п
-өлшемді кездейсоқ шаманың үлестірк функциясы
- бұл
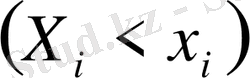 түрінде берілген теңсіздіктің бірге орындалу ықтималдығы:
түрінде берілген теңсіздіктің бірге орындалу ықтималдығы:
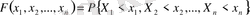
Үлестіру функциясының қасиеттері екі өлшемді жағдайға ұқсас.
Үзіліссіз п- өлшемді кездейсоқ шама үшін үлестіру тығыздығы ұғымы енгізіледі.
п-
өлшемді
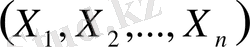 кездейсоқ шаманың үлестіру тығыздығы - бұл әрбір аргументі бойыншы бір рет алынған
кездейсоқ шаманың үлестіру тығыздығы - бұл әрбір аргументі бойыншы бір рет алынған
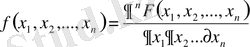
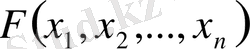 үлестіру функциясының
п
-ші аралас дербес туындысы.
үлестіру функциясының
п
-ші аралас дербес туындысы.
Дискретті п- өлшемді кездейсоқ шамалар үшін үлестіру заңы маңызды рөл атқарады.
Дискретті п- өлшемді кездейсоқ шаманың үлестіру заңы - бұл п- өлшемді кездейсоқ шаманың барлық мүмкін болатын мәндері мен олардың ықтималдарының жиынтығы:
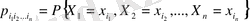
Лекция 2
Тәуелді және тәуелсіз кездейсоқ шамалар
Екі кездейсоқ шамалар жүйесінің (екі өлшемді вектор) үлестіру заңын біле отырып, жүйеге кіретін жеке шамалардың үйлесімді заңын калай анықталатындығын алдыңғы параграфта көрсетілген болатын.
Бұдан келесі сұрақ туады: жүйеге кіретін жеке шамалардың үйлесімді заңы бойынша жүйенің үйлесімді заңын табуға болмайды ма? Жалпы жағдайда бұны орындауға болмайды екен. Жүйені толығымен сипаттау үшін жүйеге кіретін әрбір шаманың үйлесімділігін білу жеткіліксіз; сонымен қатар, жүйеге кіретін шамалардың арасындағы тәуелділікті білу қажет. Бұл тәуелділік шартты үйлесімділік заңының көмегімен сипатталады.
Х үйлесімді кездейсоқ шаманың В шартындағы үлестірудің шартты функциясы деп Х кездейсоқ шаманың В шарты
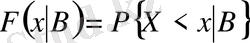
Орындалғанда х санынан кіші болуының шартты ықтималдығын айтады.
Үзіліссіз кездейсоқ шамалар жүйесі үшін үлестірудің шартты тығыздығы маңызды роль атқарады.
(Х, У) үзіліссіз кездейсоқ векторының компоненті үлестірудің шартты тығыздығы - бұл басқа бір кездейсоқ шаманың анықталған мәнді қабылдау шартынан шыққан бір кездейсоқ шаманың үлестіру тығыздығы, яғни
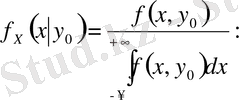
және
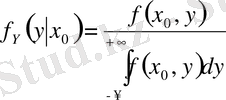
Мысалы: (Х, У) үзіліссіз векторы радиусы 1-ге тең шеңберде бірқалыпты үлестірілген, яғни
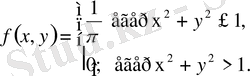
Осы вектордың компонент үлестіруінің шартты тығыздығын табу керек.
Шешуі: Алдымен бөлімінің интегралын анықтап алайық:
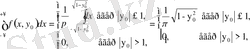
Осыған ұқсас,
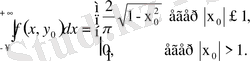
Осылайша,
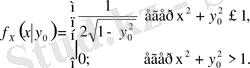
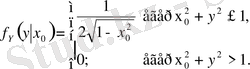
Енді дискретті жағдайын қарастырайық.
(Х, У) дискретті кездейсоқ векторының компонент шартты үлестіруі - бұл басқа бір кездейсоқ шаманың анықталған мәнді қабылдау шартынан шықғатын бір кездейсоқ шаманың бірқатар үлестіруі, яғни
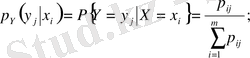
Мұндағы
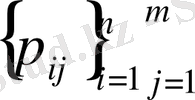 - (Х, У) -тің үлестіру заңы.
- (Х, У) -тің үлестіру заңы.
т, п - шекті немесе шексіз болуы мүмкін.
Мысалы: (Х, У) дискретті кездейсоқ векторының үлестіру заңы кестемен берілген.
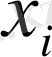
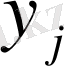
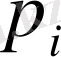
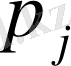
У кездейсоқ шама
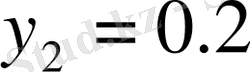
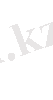 мәнін қабылдағандағы Х кездейсоқ шаманың шартты үлестіруін табу керек.
мәнін қабылдағандағы Х кездейсоқ шаманың шартты үлестіруін табу керек.
Шешуі: Кесте бағанынан
 мәніне сәйкес келетін
мәніне сәйкес келетін
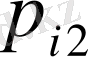 мәнін таңдап және оларды 0, 25-ке бөлгенде,
мәнін таңдап және оларды 0, 25-ке бөлгенде,
 шартпен келесі Х шартты үлестіруін аламыз:
шартпен келесі Х шартты үлестіруін аламыз:
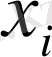
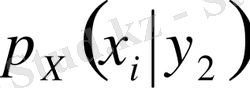
Кездейсоқ шамалар жүйесін оқып білуде әрқашанда олардың тәуелділігінің дәрежесі мен болмысына көңіл бөлу керек. Бұл тәуелділік қаншалықты кең ауқымды берілсе, соншалықты тар ауқымда да берілуі мүмкін. Кейбір жағдайларда кездейсоқ шамалардың арасындағы тәуелділік бір кездейсоқ шаманың мәнін біле отырып басқаның да мәнін дәл көрсетуге болатындай тар болуы мүмкін. Ал кейде кездейсоқ шамалардың арасындағы тәуелділікті тәуелсіз деп есептеуге болатындай әлсіз болуы мүмкін.
Нақты белгілеулерге көшейік.
Х және У кездейсоқ шамаларын тәуелсіз дейміз егер кез-келген х және у үшін
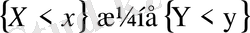 жағдайлары тәуелсіз болса, яғни
жағдайлары тәуелсіз болса, яғни
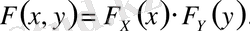
(Х, У) үзіліссіз кездейсоқ шамалар үшін үлестірудің тығыздығы сәйкес тығыздықтарға тең:
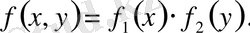
Мысалы: (Х, У) кездейсоқ векторының үлестіру тығыздығы келесі түрде берілген:
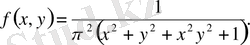
Х және У кездейсоқ шамаларының тәуелді немесе тәуелсіз екендігін анықтаңыз,
Шешуі: Бөлімін көбейткіштерге жіктегеннен шығатыны:
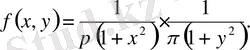
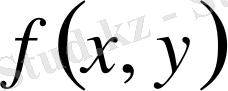 функциясының екі көбейтінді функцияға бөлінуінен, оның ішінде тек біреуінің х-қа, ал екіншісі тек у-қа тәуелді, Х және У шамалары тәулсіз болу керектігін қорытамыз. Шынында да, кездейсоқ шаманың компонент тығыздығын вектор тығыздығы арқылы өрнектейтін формуланы қолдана отырып алатынымыз:
функциясының екі көбейтінді функцияға бөлінуінен, оның ішінде тек біреуінің х-қа, ал екіншісі тек у-қа тәуелді, Х және У шамалары тәулсіз болу керектігін қорытамыз. Шынында да, кездейсоқ шаманың компонент тығыздығын вектор тығыздығы арқылы өрнектейтін формуланы қолдана отырып алатынымыз:
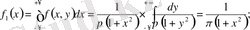
осыған ұқсас,
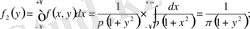
бұдан,
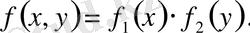
және Х және У шамалары тәуелсіз.
Тәелсіздік түсінігін п шамалы жағдайға жалпылауға болады.
Кездейсоқ
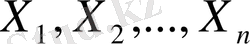 шамаларын жиыннында үзіліссіз дейміз, егер кез-келген
шамаларын жиыннында үзіліссіз дейміз, егер кез-келген
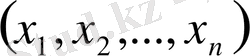 үшін жиынында
үшін жиынында
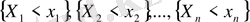 жағдайлары тәуелсіз болса.
жағдайлары тәуелсіз болса.
Ықтимал теориясының шектеулі теоремаларына қатысты көптеген нәтижелер шығатын кездейсоқ шамалар жиынында тәуелсіз деген болжамнан алынған.
Тәуелсіз кездейсоқ шамалар үшін үлестірудің шартты функциясы шартсызбен сәйкес келеді. Шынында да,
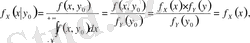
осыған сәйкес,
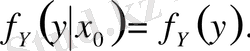
Енді тәуелді шамаларды қарастырайық.
Кездейсоқ шамалардың арасындағы ықтимал тәуелділік іс жүзінде жиі кездеседі. Егер Х және У кездейсоқ шамалар ықтимал тәуелділікте болса, бұл Х шамасының өзгеруінен У шамасы да анық түрде өзгереді дегенді білдірмейді, бұл Х шамасының өзгеруінен У шамасы да өзгеру тенденциясына ие болады (мысалы, Х шамасының өсуімен өсу немесе кему) . Бұл тенденция тек жалпы түрде ғана орындалады және бұдан қандайда бір бөлек жағдайда қайтуы мүмкін.
Ықтимал тәуелділіктегі кездейсоқ шамалар мысал ретінде, сәбидің бойы мен жасы, қандайда бір заттың шығарылуының шығысы мен кірісі, жарнама үшін шығыс және сатылатын заттың көлемі және т. с. с. болады.
Кездейсоқ шамалардың арасындағы тәуелділік дәрежесін негізінде тәуелділіктің сандық сипатының көмегімен бағалайды.
Лекция 3.
Тәуелсіздіктің сандық сипаты
(ковариация, корреляция)
Кездейсоқ вектордың негізгі сандық сипаттамалары моменттер болып табылады.
(Х, У) кездейсоқ вектордың
k, s-
ретті моменті
деп
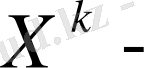 тің
тің
 -ке көбейтіндісінің математикалық күтімі:
-ке көбейтіндісінің математикалық күтімі:
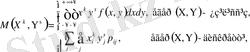
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz