Атомның магниттік моменті

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

1. 1. Атомның магниттік моменті

Орбиталдық магниттік моменті. Атомның L механикалық моментімен магниттік момент байланысқандығы бұрын айтылған болатын. Сутегі атомындағы электронның орбиталық қозғалысынан пайда болатын η-дің L-мен байланысы үшін классикалық өрнек алынған болатын. Кванттық теорияда η және L шамаларын ή және Ĺ операторларымен алмастыру қажет:

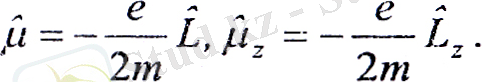(1)

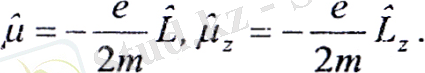Осыдан электронның магниттік моментінің қасиеттерін зерттеу ή және Ĺ операторларының қасиеттерін зерттеуге келтірілетіндігі көрінеді. ή және Ĺ, және операторларының бір-бірінен айырмашылығы тек тұрақты көбейткіш болатындықтан, бұлардың қасиеттері өте ұқсас: магниттік және механикалық моменттер бірдей ережелер бойынша квантталады.

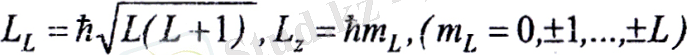Стационарлық күйде тек η L магниттік моменті модулінің және оның кез келген Z өсіне проекцияларының біреуінің нақты мәндері болады. (1) және

өрнектерін еске алып

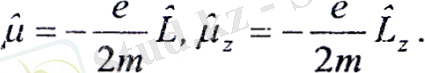ή және операторларының меншікті мәндерін жазамыз:

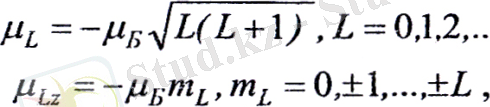(2)

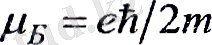(3)

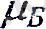мұндағы - Бор магнетоны: Ол магниттік момент

квантының ролін атқарады.

Атап өтетін нәрсе:

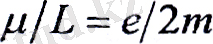Магниттік моменттің механикалық моментке қатынасы, яғни

(4)

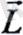гиромагниттік қатынас деп аталады; жоғарыда келтірілген формулалардағы «-» таңбасы және векторлары бағыты бойынша өзара қарама-қарсы болатындығына нұскайды.

Спиндік магниттік момент және оның кез келген z өсіне проекциясы былай анықталады.

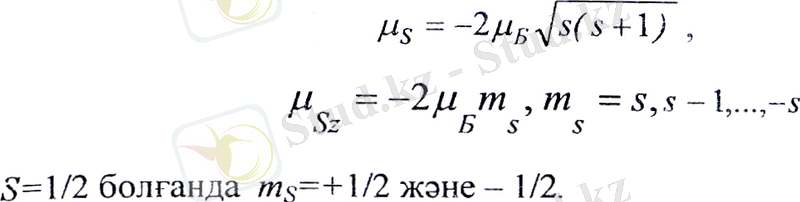(5)

(6)

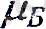Электронның спиндік магниттік моменті бір Бор магнетонына тең деп айту қабылданған. Бұлай айту мынаған байланысты: магниттік моментгі өлшегенде эдетте оның проекциясы өлшенеді, ал ол бір -ға тең.

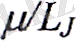Атомның толық магниттік моменті. Спиннің екі еселенген магнетизмі салдарынан толық моменттердің гиромагниттік қатынасы едәуір күрделенеді. Ол L, S және J кванттық сандарына тәуелді болады. Кванттық теорияда жүргізілген тиісті есептеу η магниттік моменті және оның z өсіне проекциясын табуға мүмкіндік берді:

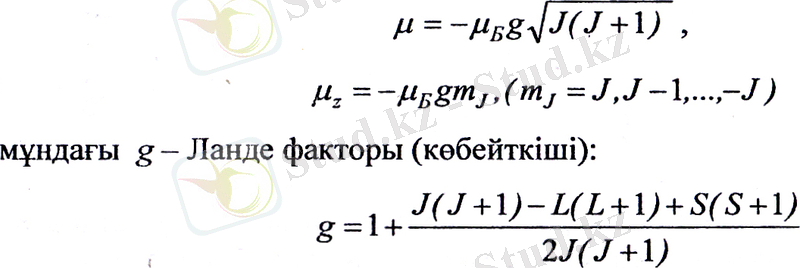
(7)

(8)

(9)

1. 2 штерн және герллх тәжірибесі

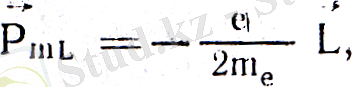Біз электронның, орбиталық моментінің сыртқы магнит өрісінде кеңістіктік квантталғандығын қарастырдық. Бор теориясы бойынша ондай квантталу болмауы керек, орбиталық момент кеңістікте әр түрлі, кез келген бағытта болып, әр түрлі мәндер қабылдауы қажет. Міне, бұл Бор теориясының кванттық механиканың қорытындыларымен қайшылықтарының бірі. Бұл қайшылық не себептен болады деген сұрақ туады. 1922 жылы қойылған О. Штерн және В. Герлах тәжірибесінің мақсаты әр түрлі химиялық элементтердің

(10)

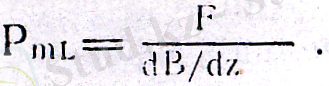- электрон массасы, е. - электрон заряды) магниттік моменттерін өлшей отырып, орбиталық, және магниттік моменттерінің квантталуын зерттеу болды. Өлшеулерді жүргізу үшін Менделеев таблицасының бірінші группасындағы химиялық элементтердің атомдарын қарастырды. Себебі, бұл группадағы элементтердің атомдарының сыртқы валенттік қабатында бір валенттік электрондары болады, ал қалған ішкі қабаттардағы электрондардың орбиталық, және магниттік моменттері бір-бірімен өзара компенсацияланған. Сонда тәжірибеде, тек бір валентті электронның магниттік моментін өлшесе болғаны:

(11)

Мұндағы В - магнит өрісінің индукциясы, Ғ - магнит өрісінде зарядталған бөлшекке әсер етуші күш, бөлшектердің z өсінің бойымен ауытқуы қарастырылады. Штерн және Герлах тәжірибесінің схемасы-суретте берілген. А атом көзінен, белгілі бір температураға дейін қыздырған кезде, күміс атомдары ұшып шығады. Әдейі формада істелген NS - электромагнит көмегімен күшті біртексіз магнит өрісі В алынады.

Күшті біртексіз магнит өрісінен өткен күміс атомдары Ф фотопластинкаға соғылады. Егер атомның орбиталық, магннттік моменттері магнит өрісінде әр түрлі кез келген мәндерді қабылдайтын болса, күміс атомдары фотопластинка да негізінен орта жернде шоғырланған болар еді. Күміспен және бірінші периодтағы басқа элементтердің атомдарымен жүргізілген тәжірибелер,

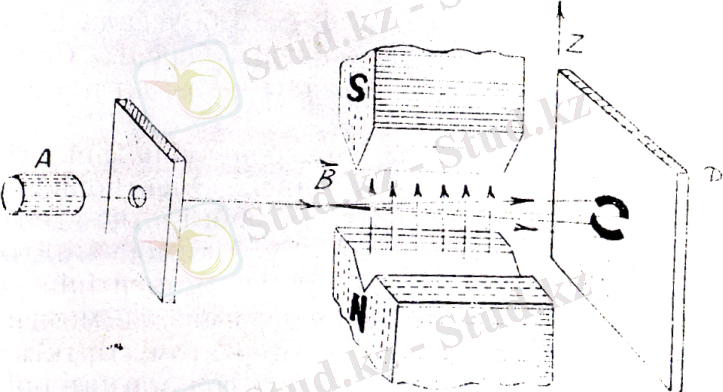
атомдардың магнит өрісінде екіге бөлінетінін көрсетті, яғни қарастырылып отырған атомдардың магниттік моментінің бағдарлану мүмкіндігі екеу екенін көрсетті. Алдыңда айтып кеткендей, Штерн және Герлах тәжірибелерінде сыртқы I валентті электронның, магниттік моментін өлшеген:

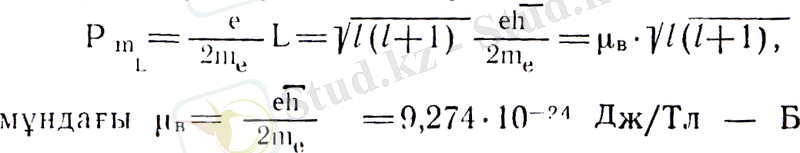
Бор магнетоны

деп аталатын тұрақты шама. Атомдардың және электронның магниттік моменттері Бор магнетонымен беріледі.

Тәжірибеден dB/dz мәні белгілі, ал F күшін атомдардың ауытқуы арқылы өлшеп, (11) формуласынан берілген элемент атомдарының, дәлірек айтсақ, электрондарының магниттік моменті табылған. Штерн және Герлах атомның магниттік моментінің магнит өрісіне проекциясы сан жағынан Бор магнетонына тең екенін тапқан. Міне, сөйтіп Штерн және Герлах тәжірибелері электрондар мен атомдардың импульс моменттерінің (магниттік моменттерінің) сыртқы магнит өрісінде дискреттік квантталған мәндерді қабылдайтынын және магнит моментінің сандық мәні Бор магнетонына еселі болғанын практика жүзінде дәлелдеді.

1. 3 Электрон спині

Сонымен Штерн және Герлах тәжірибесіндегі алынған элементтер атомдарының күйін қарастырайық. Менделеев таблицасының I группасындағы элементтердің электрондары s, яғни орбиталдык импульс моменті ι = 0 күйде болады. Сонда, тәжірибеде өлшеніп алынған қандай импульс моменті (магниттік момент) деген сұрақ туады?

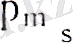Бұл сұракка жауап беру үшін 1925 жылы Д. Уленбек және С. Гаудемит электронның орбиталық импульс моментімен қатар меншікті механикалық импульс моменті болады деп есептеді. Оны «спин» деп атады (ағылшын тілінен аударғанда «ұршық») және оған байланысты пайда болатын меншікті магниттік момент болады. Ал меншікті механикалық импульс моменті,

яғни спин қалай пайда болады? Әуелгі кезде Уленбек және Гаудемит спин электрон-шариктін өз өсінен айналуынан пайда болады деген жорамал айтты. Бірак кейіннен, келесі жай есептеулердің нәтижесі бұл жорамал дұрыс емес екенін дәлелдейді. Лоренцтің есептеуінше электрон радиусы

Салыстырмалық теориясы бойынша жарық жылдамдығынан артық жылдамдық болмауға тиіс, яғни электрон-шариктің өз өсінен айналуы туралы жорамал дұрыс емес екен. Қазіргі көзқарастарга қарағанда спин дегеніміз электронның кеңістіктегі қозғалысына байланыссыз, өшпейтін өзіне тән механикалық моменті. Спин-электронның массасы, заряды сиякты касиетті. Кванттық механика зандары бойынша спин де квантталған; яғни дискреттік мәндерге ие болуы керек, әрекет квантының бірлігімен өлшенеді.

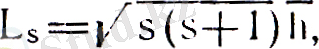(13)

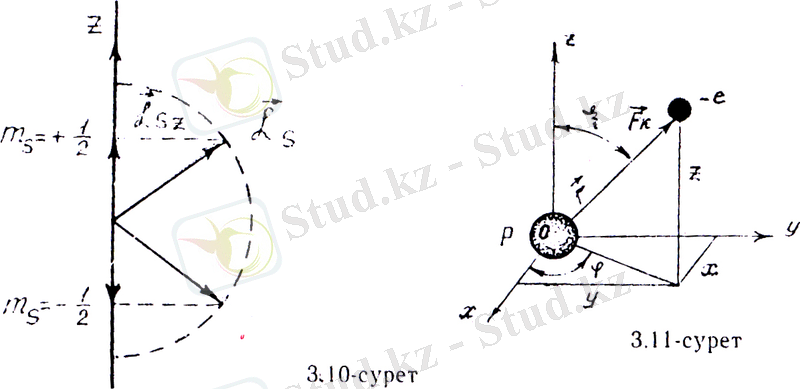
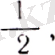мұндағы s - кванттық сан спиндік кванттық сан деп аталады. Сонда, Штерн және Герлах тәжірибесіндегі сыртқы магнит өрісі бағытымен бағыттас z өсіне түсірілген спиннің проекциясы болады да, магнит өрісінде векторы 2s+l әр түрлі багытта бағдарлана алады, яғни электронның, бағдарлануы екі бағытта:

2-s+l -=2. Сонда s = яғни берілген магнит өрісінің бағытына

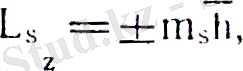проекциясы

(14)

мұндағы - магниттік спиндік сан. Тәжірибедегі бағдарлану

екі бағытта = ±1/2. Бір электрондардың спині +

ал енді біреулерінің спині-болады екен.

Басқа да элементар бөлшектер - протон, нейтрон мсзондардың да спиндері болады. Жартылай тақ, спинді бөлшектері фермиондар (электрон, протон, нейтрон және т. с. с), ал спині жоқ немесе жұп спинді бөлшектерді бозондар (фотон, л-мезон және т. с. с. ) деп атайды.

Сонымен атомдағы электрондардың күйіп сипаттау үшін 4 кванттық сан (бас кванттық -n, орбиталық - l, магинттік - nl және спиндік - s) керек екен.

1. 4 Атом құрылысы және оның спектрлері

Алдымызға, өткен тақырыптарды қорытындылай отырып, біз мынадай сұрақ қойсақ: атомның құрылысы қандан, электрондар қалай орналасқан? Бұл сұрақтарға кванттық механика тұрғысынан қарап жауап беру керек?

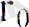Ол үшін ең қарапайым атом - сутегі атомын қарастырайық. Сутегі атомы бір протоннан және бір электроннан тұрады. Протон массасы электрон массасына қарағанда өте үлкен болғандықтан протонды қозғалмайды деп есептейміз. Сопда ядроны - протонды ара қашықтықта (радиус) айналып жүретін бір электронның потенциалдык энергиясы (Кулон заңын ескерсе, е - элементар заряд)

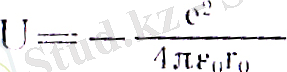(15)

болады. Miнe, осы ядроны айналып қозғалатын электрон үшін Бор теориясында (біз алдыңғы параграфтарда қарастырып кеткен) электрон орбиталары туралы түсінік енгізген. Ал, шынында кванттық механика тұрғыснан қарастырсақ, орбита туралы түсінік өзінің мағынасын жоғалтады (Гейзенбергтің анықталмағандық қатынасынан білеміз) . Сонда орбитаны қандай түсінікпен ауыстырамыз? Атомдағы электрон күйін біз тек электрон бұлты, яғни электронның орнын көрсететін ыктималдықтың үлестірілуі арқылы сипаттаймыз.

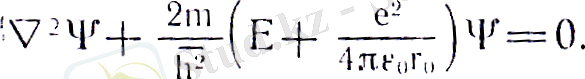(16)

Сфералык координаталар системасын қолданамыз-г, ф, £, себебі қарастырып отырған электронымызға протон (р) тұргысынан әсер ететін күш, центрлі-симметриялық күш болып табылады. (16) теңдеуінің, шешімі Е энергияның кез келген оң және теріс дискреттік мәндері үшін

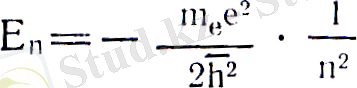(17)

п=1, 2, 3, . . . (17) қатынасының дискреттік мәндері сутегі атомының энергетикалық спектрін E1, Е2, Е3, . . . , Еn құрайды, ал n - бас кванттық сан, энергетикалық сипаттамасы болып табылады. Суретте электронның потенциалдық энергиясының электронның, ядродан (г) ара қашықтығына байланыстылығы берілген. Суреттен Е<0 болғанда, электрон қозғалысы шектелген, гиперболалық потенциалдық шұңқырдың ішінде болады. Ал Е>0 болса, электрон қозғалысы шектелмеген, атомнан бөлініп кете алады. Бұдан электронның теріс энергиялы күйі, оның ядромен байланыскан күйі болып табылады. Бірдей энергиялары бар, яғни бас кванттық сандары бірдей, бірақ әр түрлі мәні бар күйлерді ерекшеленген, азғынданған күйлер дейді.

(16) теңдеудін меншікті мәндері үш бүтін сандык параметрлерге байланысты

n және

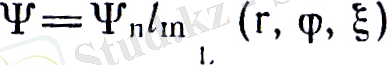(18)

l 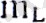және параметрлері, алдыңғы тақырыптарда қарастырған орбиталық және магниттік кванттық сандар. Сутек атомының негізгі (ең төменгі) энергетикалық күйінде n=1, l=0, -0,

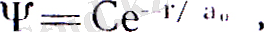яғни ls күйі сфералық симметриялық күй. Бұл күйде электрон ядродан r қашықтықта кез келген нүктеде бірдей ықтималдықпен табылады, сфера түріндегі электрон бұлтын түзеді, яғни ф және ζ бұрыштарына тәуелсіз. Сондықтан бұл күйде толқындық, функция ψ тек қана электронның ядродан r0 ара қашықтығымен анықталады. ls күйдегі электрон үшін Шредингер теңдеуі мына түрге келеді:

(19)

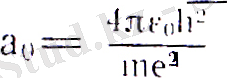
сутегі атомы үшін тұрақты шама және формуласындағы

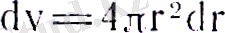1-ші Бор орбитасының радиусына тең. С - ықтималдықты нормалау шартымен аныщқталатын тұрақты шама. Электронның бір

көлемде табылу ықтималдығын нормалау шарты:

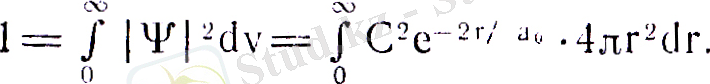
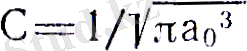
Интегралдан, екенін тауып, (19) формуласына қойсақ. ls күйдегі электрон үшін

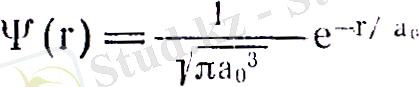(20)

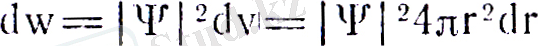электронның. Dv көлемінде табылу ықтималдығы

(20) формуласындағы толқындық, функция мәнін қойсақ

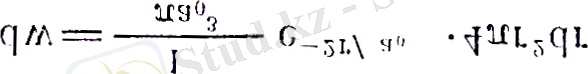
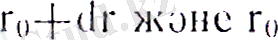
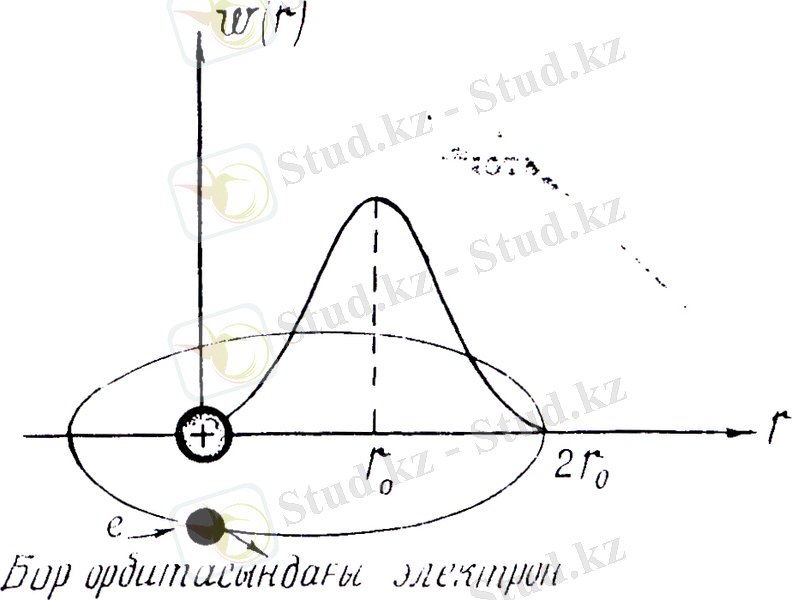
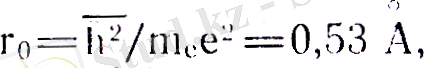Электронның, ара қашықтығында табылу ықтималдығының тығыздығы w(r) негізгі күй үшін ара қашықтықтың функциясы және оның максимумы 1-ші Бор орбитасы радиусының ұзындығына тең.

Сутегі атомының электроны сырттан белгілі бір энергия алып n= 2 күйгe көшсін делік. Бұл күйде l = 0, немесе l = 1, ал w(r) функциясының r-ге тәуелділігі.

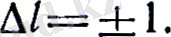Сутегі тәріздес ионданған атомдар (мысалы Не+, Li++) күйлерін сутегі атомы сияқты сипаттауға болады. Атомның жарық шығаруы немесе жұтуы электрондарының бір энергетикалық деңгейден екінші денгейге ауысқанда болатынын біз қарастырғанбыз. Кванттық механикада орбиталық кванттық сан үшін іріктеу ережесі болады: