Физика есептерін шешудің алгоритмі және тиімді оқыту әдістері


Физика есептерін шешу маңызын арттыру жолдары
Физиканы оқып үйрену мен болып жатқан физикалық процесстерді жете түсіну барысында физикалық есептерді шешудің маңызы зор. Өтілген тақырыпты жетік меңгеру үшін, оның физикалық мағанасын ашу, есеп шығару сияқты жолдар оқушының алған білісін тереңдете түседі. Физикалық есептерді шешуді әр оқытушы немесе ізденуші өз тәжірибесінен, оқыту әдісімен бар шеберлігін қолдана отырып, оқушы санасына жеткізуге тырысады. Айталық, кейбір авторлардың (1, 2, 3) ұсынып жүрген физикалық есептерін шешіп үйрену әдістерін бірнеше сатыға бөліп қарастырғанын көреміз. Оны бірден күрделі жолмен шешей, жеңіл жолдарын қарастыру керек болады. Себебі физиканың кейбір тарауларын жеке алып қарасақ, ол физиканы жаңа оқып жүрген оқушы үшін өте ауыр, тіпті кейде оның жетік меңгерген оқушыларға немесе оқытушыларға арналғанын байқайсын. Сондықтан жекелеген сатыларды барлық есептерді шешуге олануға болмайды.
Қазіргі кезде арнайы әдістер және есеп шығару тәсілдері бар. Енді әрбір оқытушы физика пәнін оқытуда өз іс-тәжірибесін жете пайдаланып, оқушының осы пәнге деген ынта-жігерін оята білуге тырысу керек. Осындай жағдайда физикалық есепті неден бастау керек, қандай физикалық заңдарға, құбылыстарға сүйенген жөн? - деген сұрақтар туындайды. Бұл сұрақты берілген есепті оқи отырып, жауап береміз. Есеп шығару барысында физиканың тек бірғана бөлімін оқып қоймай, басқада бөлімдерін, тіпті кейде басқа да пәндермен (мысалы: химия, астрономия, математика, т. б. ) байланысын ескерген жөн. Есепті мәтіндік, графикалық, экспериментальды т. б. түрлерін білеміз. Есеп шығарудың өзі көп ізденісті талап еткендіктен ен тиімдісі - физикалық есептердің түрлеріне қарай шешу, алгорнитмдерін жасау болып табылады. Алгоритм есептерді әрі түсінікті жолмен шығаруға көмегін тигізеді. (Схеманы қараңыз)
Схемада есеп шығару жолдары рет-ретімен берілген. Ол есептің барлық түрлері үшін жасалған, оқушыларға қарапайым, әрі түсінікті, әрі шешуге қолайлы. Мұндай талдау арқылы шығарылған есептер оқушының физикалық процесстердің теориясынан түсінбегендерін есеп шығару барысында толық түсінуге септігін тигізеді.
Физикалық есептерді шығаруда компьютерді пайдалану өте қолайлы. Қазіргі электронды техниканың өркендеген заманында барлық мектептерде, оқу орындарында компьютермен қамтамасыз етілгендіктен, оны барлық сабақтарда пайдалану керек. Программалау тілдері арқылы әр есепке программалар құруға болады. Бұл бізге есептегі физикалық шамаларға әр түрлі мәндер бере отырып бірнеше нәтижелер алуымызға борлады. Әсіресе екі шаманың қатынасына графиктер тұрғызу, сондай-ақ физикалық эксперименттердің зертханалық әдістерін жүргізудің маңызы зор. Оқушының компьютермен жұмыс істеу арқылы оның физика пәніне, физикалық есептерді шешуге деген қызығушылығын арттыруға болады. Аталған алгоритм бойынша нақты мысал келтіре кетейік:
Есеп.
Жазық конденсатордың астарларының арақашықтығы d=1 см және потенциалдар айырмасы U=200B. Осы конденсатордың төменгі астарына қалыңдығы d
2
= 8мм эбонит
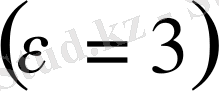 орналастырылған. Эбониттің байланысқан зарядтарының беттік тығыздығын анықтау керек.
орналастырылған. Эбониттің байланысқан зарядтарының беттік тығыздығын анықтау керек.
1) есепті берілген схема бойынша шешейік. Есептің мәтінін мұхият оқып шыққан соң, қысқаша математикалық белгілермен берілгенін жазамыз.
Берілгені: БЖ
d=1см 10 -2 м
U=200B
d 2 =8мм 10 -3 м

Табу керек σ=?
2) Бұл есептің мақсаты, эбонит пластинканың (эбонит пластинка диэлектрик, ток өткізбейтін орта ретінде қарастырылып отыр) зарядталған беттегі зарядтың беттік тығыздығын σ деп белгілеп отырып анықтау. Есепте конденсатор астар-ларының арақашықтығы, потенциалдық айырмасы және эбонит пластинканың қалыңдығы берілген. Біз қарастырған ортаны біртекті деп алайық. Эбонит пластинканың диэлектрик өтімділігін
 ке тең.
ке тең.
3) Есептің мазмұнына сай түсінікті болу үшін сүретін салайық.
Мұндағы:
d - конденсатор астарларының арақашықтығы;
d 2 - эбонит пластинканың қалыңдығы;
Е 1 - конденсатор кернеулігі;
Е 2 - эбонит пластинканың кернеулігі.
4) Есеп электро динамика бөлімінің электр сыйымдылығы және конденсатрлар тақырыбына берілген. Осы тақырыптар бойынша негізгі формулаларға тоқталайық.
5) Есепте берілген конденсаторлардың астарларының арақашықтығы d=1см 10 -2 м, эбонит таяқшаның қалыңдығы d 2 =8мм 10 -3 м етіп бірліктер жүйесіне келтірейік.
6) Осы 2-5 бөлімдер бойынша талдауды жалғастырайық. Есепті шешу үшін өрістің кернеулігі потенциалдар айырмасымен мына формула арқылы байланысатынын ескерсек:
E=U/d, бұдан
U=Ed
Осыған орай, конденсатордың оң астары үшін потенциалдар айырмасын жазайық U 1 =E 1 d 1 , ал, айырмасы U 2 =E 2 d 2 .
Демек, жалпы конденсатор үшін толық потенциалдар айырмасын былай жазылады:
U=E 1 d 1 +E 2 d 2 (1)
Диэлектриктрлік өтімділік деген диэлектриктің электрлік қасиеттерін қарастыру үшін енгізілген шама. Ортаның диэлектрлік өтімділігі дегеніміз- біртекті диэлектрлік ішіндегі электр өрісінің кернгеулігін модулі, вакуумдағы өріс кернеулігінің модулінен неше есе кем екенін көрсететін физикалық шама. Олай болса біздің сүретіміз бойынша диэлектрлік өтімділік мынаған тең:
 (2)
(2)
Мұндағы E 1 - біртекті диэлектрлік ішіндегі кернеулік, E 2 - эбонит пластинканың кернеулігі.
(Бұл формула кеңістіктің бәрін толтырған біртекті орта үшін және конденсатор ішіндегі біртекті пластина үшін орындалады. Кез келген түрдегі дене үшін E 1 және E 2 арасындағы тәуелділік күрделірек болады. Дененің пішімі және вакуумдегі өріс кернеулігіне қатысты анықталады. )
(2) формуладан
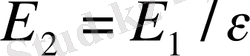 (3)
(3)
(1) формулаға
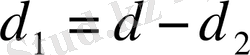 (сүрет бойынша табамыз) қойып былай жазайық,
(сүрет бойынша табамыз) қойып былай жазайық,
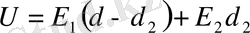
Осы формуладан
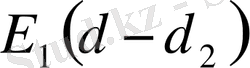 табайық,
табайық,
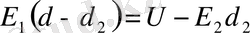
бұл формуладан E 1 - ді табамыз,
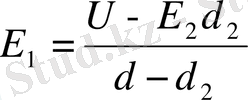
Табылған формула (3) формулаға қойып мынаны аламыз:
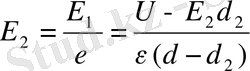
Осы теңдіктен Е 2 - ні табу үшін, математикада пропорция амалын қолданамыз.
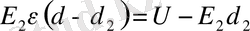
Бұдан
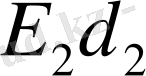 теңдігін сол жағына шығарайық, сонда
теңдігін сол жағына шығарайық, сонда
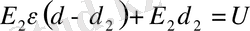 Е
2
-ні
жақшаның сыртына шығарамыз, одан мынадай теңдеу шығады:
Е
2
-ні
жақшаның сыртына шығарамыз, одан мынадай теңдеу шығады:
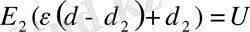
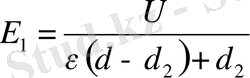 (4)
(4)
Зарядтың беттік тығыздығын мына формуламен анықталатыны белгілі:
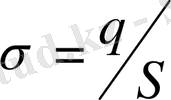 (5)
(5)
Зарядтың беттік тығыздығы беттегі зарядтың сол бет ауданына қатынасына тең екен. Кернеулікпен беттік заряд тығыздығы арасындағы қатынас мынадай байланыс арқылы табылатынын біле отырып:
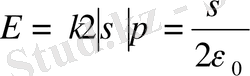 (6)
(6)
Бұл тек біртекті зарядталған денеге жақын орналасқан электр өрісінің кернеулігін есептеу үшін қоланылады.
Конденсатор астарлары арасындағы кернеулік Е әр конденсатор астарындағы Е 1 және Е 2 кернеулердің қосындысына тең.
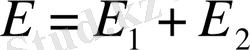 (7)
(7)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz