Функция ұғымы, берілу әдістері мен графигі: тура және кері пропорционалдық


Функция және оның графигі
Функция ұғымын анықтау
Функция аса маңызды математикалық ұғымдардың бірі және де ол заттар мен құбылыстардың өзара байланысын бейнелейді.
Бүгінде функцияны анықтаудың әр түрлі жолдары белгілі. Солардың бірінде функция ұғымы бастапқы ұғым ретінде алынады.
Енді бірінде бастапқы ұғым ретінде бейнелеуді алалды да, функция деп бір X жиынын екінші Y жиынына бейнелеуді түсінеді. Бұл жайдайда xєX элементпен yєY болатын, бір және тек бір ғана элемент жұптүзей алынатына ерекшеленеді. Сонда функцияныз белгілеп көрсету үшін
 , φ, ψ және т. с. с. символдар пайдаланады. Ал X жиыны функцияның анықталу облысы және Y жиынын функцияның мәндерінің облысы деп атайды.
, φ, ψ және т. с. с. символдар пайдаланады. Ал X жиыны функцияның анықталу облысы және Y жиынын функцияның мәндерінің облысы деп атайды.
Анықталу облысы X және мәндерінің облысы Y болатын
 (x) функцияны символдар арқылы мына түрде X → Y немесе айнымалылырдың көмегімен x
xєx
→y
yєy
деп белгілейді, сонда функция мәнінің белгісі ү-тің орнына
(x) функцияны символдар арқылы мына түрде X → Y немесе айнымалылырдың көмегімен x
xєx
→y
yєy
деп белгілейді, сонда функция мәнінің белгісі ү-тің орнына
 символын жиі қолданады. Бұл жайдайда ункцияны x→
символын жиі қолданады. Бұл жайдайда ункцияны x→
 (x) түрінде белгілейді. Кейде x жиыны элементтерін функцияның аргументі деп атады да,
(x) түрінде белгілейді. Кейде x жиыны элементтерін функцияның аргументі деп атады да,
 -ті аргумент x-тің немесе анымалы x-тің функциясы дейді.
-ті аргумент x-тің немесе анымалы x-тің функциясы дейді.
Сандық функцияның анықтамасы
Бейнелеулер, қатынастар және сәйкестіктер табиғаты әр түрлі жиындарда берілуі мүмкін екендігі белгілі, ендеше олардың дербес түрі болып табылатын функцияның да анықталу облысы мен мәндерінің облысы әр түрлі жиындар бола алады.
Ал математика курсында негізінен сандық және нүктелік жиындар қарастырылады, өйткені осы жиындарда функцияның әр түрлі қасиеттерін қарастыру өте қолайлы.
X және Y қандай да бір сандық жиындар болсын /X
 R, Y
R, Y
 R/.
R/.
Анықтама.
X жиынында анықталған, ал мәндері Y жиынында болатын сандық функция деп ербір xєX санына бір ғана yєY санын сәйкес қоятын
 сәйкестікті айтады.
сәйкестікті айтады.
Сандық функцияны негізінен x→
 (x), xєX немесе y =
(x), xєX немесе y =
 (x) түрінде белгілейміз. Сонда сандық X жиыны -
(x) түрінде белгілейміз. Сонда сандық X жиыны -
 функциясының анықталу облысы, ал
функциясының анықталу облысы, ал
 (x) түріндегі барлық сандардан тұратын, мұндағы xєX, сандық Y жиыны
(x) түріндегі барлық сандардан тұратын, мұндағы xєX, сандық Y жиыны
 -тің мәндерінің жиыны болып табылады.
-тің мәндерінің жиыны болып табылады.
Және де
 функциясының анықтау облысын D (
функциясының анықтау облысын D (
 ) арқылы; ал оның мәндерінің жиының Е (
) арқылы; ал оның мәндерінің жиының Е (
 ) арқылы да белгілейді.
) арқылы да белгілейді.
Функцияның берілу тәсілдері және оның графигі
Функцияны көрсетіп беру үшін сандық X жиынды және әрбір xєX санына сәйкес келетін y санын, яғни функцияның мәнін табу үшін қолданылатын тәсілді көрсетіп беру керек болады.
Жалпы алғанда, егер әрбір xєX санына қанда да бір y саны сәйкес қойылса, онда X
 R жиынында сандық функция берілген дейді. Сонда әрбір y =
R жиынында сандық функция берілген дейді. Сонда әрбір y =
 (x), xєX функциясымен, оның мәндерімен тұратын, яғни
(x), xєX функциясымен, оның мәндерімен тұратын, яғни
 (x), xєX, сандық Y
(x), xєX, сандық Y
 R жиыны байланысты болады.
R жиыны байланысты болады.
Функцияны әр түрлі тәсілмен анықтап береді. Соның ішінде ең көп тарағы - функцияның аналитикалық тәсілмен берілуі, яғни аргументтің мәні бойынша функцияның сәйкес мәнін табу кезінде орындалатын амалдардың жиынтығын көрсететін формула арқылы функцияның берілуі. Сонда функцияның анықталу облысы көрсетіледі. Егер формула арқылы берілген функцияның анықталу облысы айқын түрде көрсетілмесе және ешқанда қосымша шектеулер келтірілмесе, онда функцияның анықталу облысы, айнымалының осы формуланың мән-мағынасы болатындай барлық мәндерінен тұрады. Мысалы:
3x-1,
егер
x
 0
0
y=
2x,
егер
x
 0, y=
0, y=
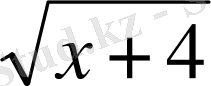
Функцияны аргументтің мәндері және функцияның сәйкес мәндері арасындағы сәйкестік заңын сөз арқылы сипаттаудың келтіруімен де анықтап беруге болады. Осындай функциялар үшін арнайы таңбалардың да енгізілуі орынды. Мысалы: y=[x], xєR, мұндағы {x}=x-{x}, x санының бөлшек бөлігі.
Функцияны, оның графигі деп аталатын, координаттық жазықтың қандай да бір сызығының көмегімен анықтап беруге болады. Жалпы алғанда, әрбір функциямен қандай да бір сызық - осы функциның графигі байланысты. Алайда бұған кері ұйғарым әрдайым тура бола бермейді, өйткені xєX болатын x-тің берілген мәнінде оған сәйкес келктін функцияның бір ғана мәні y бар болады. Сондықтан ордината осіне параллель жүргізілген әрбір түзуде функцияның графигіне тиісті бірден артық болмайтын нүкте ғана жатуы тиіс. Мәселен, шеңбер қанда да бір функциның графигі болып табылмайды, өйткені шеңбердің екі нүктесі жататын ордина осіне параллель түзулер бар.
y
y=
 (x)
(x)
x
Жалпы алғанда y
 (x), xєX функциясының графигі деп xєX ал y=
(x), xєX функциясының графигі деп xєX ал y=
 (x) болатын (x; y) парлардың; яғни (x,
(x) болатын (x; y) парлардың; яғни (x,
 (x) ), xєX түріндегі парлардың жиынын айтады. Осындай реттелген әрбір парға координаттық жазықтықтың абсциссасы x және ординатасы y=
(x) ), xєX түріндегі парлардың жиынын айтады. Осындай реттелген әрбір парға координаттық жазықтықтың абсциссасы x және ординатасы y=
 (x) бір ғана нүктесі сәйкес келкді. Ендеше координаттық жазықтықтың дәл осындай нүктелерінің жиыны y=
(x) бір ғана нүктесі сәйкес келкді. Ендеше координаттық жазықтықтың дәл осындай нүктелерінің жиыны y=
 (x), xєX функциясының графигін кескіндейді.
(x), xєX функциясының графигін кескіндейді.
Кейбір жағдайларда, аргументің таңдап алынған мәндерінде функцияның мәндерін табуға мүмкіндік беретіндей кесте құруға болады. Осындай кестелердің мысалдары ретінде сандардың квадраттарының және кубтарының кестелерін, тригонометриялық функциялар мәндерінің кестелерін және т. б. атаған жөн. Әсіресе, X жиыны шектеулі болса, онда анымалылардың сәйкес мәндерінің кестелерін пайдаланған тым қолайлы Бұл жағдайда функция кестелік тәсіл арқылы анықтап берілген болып табылады.
Дегенмен функцияның ананлитикалық және графигтік тәсілдермен берілуі оны оқып-үйренуге өте қолайлы. Осыған орай, аналитикалық тәсілмен берілетін нақты функцияларды анықтайық. Біз оларды мынадай ретпен оқып-үйренеміз:
а/ қандай да бір функцияға киліктіретін, яғни оны енгізу себепші болатын нақты жағдайларды қарастырамыз;
ә/ функцияның анықтамасын тұжырымдаймыз және оны формуламен анықтап береміз де, осы формуланың құрамындағы параметрлерді зерттейміз;
б/ оқып-үйренетін функцияны график арқылы кескіндеп көрсетеміз;
в/ функцияның кейбір касиеттерін қарастырамыз.
Тура пропорционалдық, оның қасиеттері және графигі
t - жаяу адамның қозғалыс уақыты, s - оның жүрген жолы және ол v км/сағ жылдамдықпен бірқалыпты қозғалыста болсын делік. Сонда v тұрақты болғанда t-ның әрбір мәніне s-тің бір ғана мәні келеді және ол s= v ∙ t формуласымен есептеледі. Сондықтан s= v ∙ t формуласы, тура пропорционалдық, яғни s дегеніміз t-ға тура пропорционал, деп аталатын функцияны анықтап береді.
Анықтама.
Тура пропорционалдық деп y=kx формуласыны, мұндағы, x тәуелсіз айнымалы, ал k
 0 және kєR, көмегімен берілетін функцияны айтады.
0 және kєR, көмегімен берілетін функцияны айтады.
Бұл формула айнымалы y-тің айнымалы x-ке тәуелділігін, яғни анымалы y-тің анымалы x-ке тура пропорционал екендігін анықтап береді, мұндағы k - пропорционалдық коэффициент.
Ал y=kx функциясының қасиеттері болады.
1. Оның анықталу облысы нақты сандардың R жиыны.
2. Оның графигі координаталардың басы арқылы өтетін түзу сызық, өйткені x=0, y=0 және
 k
k
 0, kєR. Сонымен бірге, егер k>0 болса, онда түзу I және III координаталық ширектер ақылы өтеді, ал егер k<0 болса, онда II және IY координаталық ширектер арқылы өтеді. Графигі салу үшін бір ғана, мәселен нүктесін табу жеткілікті болып есептеледі.
0, kєR. Сонымен бірге, егер k>0 болса, онда түзу I және III координаталық ширектер ақылы өтеді, ал егер k<0 болса, онда II және IY координаталық ширектер арқылы өтеді. Графигі салу үшін бір ғана, мәселен нүктесін табу жеткілікті болып есептеледі.
y y
y=kx (k>0) y=kx (k<0)
x x
3. Егер k>0 болса, x>0 болғанда, онда y>0,
x<0 болғанда, онда y<0.
Егер k<0 болса, x>0 болғанда, онда y<0,
x<0 болғанда, онда y>0.
4. Егер k>0 болса, онда R жиынында өседі, ал k<0 болса, онда кемиді.
5. Егер x және y айнымалылардың мәндері оң сандар болса, онда x айнымалы мәндері бірнеше есе артса y айнымалы мәндері де сонша есе артады, яғни
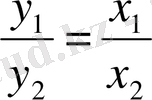 болады.
болады.
Кері пропорционалдық, оның қасиеттері және графигі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz