Фредгольм теоремалары мен симметриялық интегралдық теңдеулер: меншікті мәндер, ортонормаланған функциялар және Гильберт-Шмидт теоремасы


4. 4. Фредгольм теоремалары.
Жоғарыдағы талқылаған мәселелер нәтижесінде келесі теоремаларды тұжырымдауға болады.
- теорема (Фредгольмнің 1- теоремасы) . Егер λ регуляр сан, ал ядросы үзіліссіз
(61)
біртекті емес интегралдық теңдеудің жалғыз ғана үзіліссіз шешімі бар болады, ол шешім
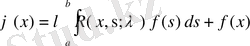
формуласымен анықталады.
Бұл теоремадан салдар ретінде мынадай тұжырым шығады.
- теорема. Егер λ регуляр сан болса, онда біртекті
(62)
теңдеудің тек нольдік яғни
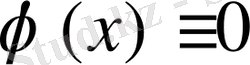 шешуі ғана бар болады. Сондықтан егер біртекті (62) теңдеуінің нольдік емес шешімі бар болса, ол жағдай тек λ шектік сан болған жағдайда орындалады.
шешуі ғана бар болады. Сондықтан егер біртекті (62) теңдеуінің нольдік емес шешімі бар болса, ол жағдай тек λ шектік сан болған жағдайда орындалады.
- теорема. Егер λ0меншікті сан болса, онда біртекті (62) теңдеуініңшешімі бар болады.
Дәлелдеуі. Меншікті мән λ 0 резольвентаның r еселі полюсі болсын, демек резольвента мына Лоран қатарына жіктелсін:

мұндағы
 . Интеграл теңдеуді
. Интеграл теңдеуді
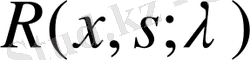 үшін Лоран қатармен ауыстырып, одан кейін оның екі жағын
үшін Лоран қатармен ауыстырып, одан кейін оның екі жағын
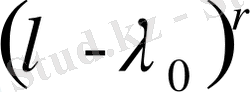 - не көбейтіп, сонан соң
- не көбейтіп, сонан соң
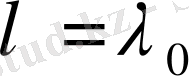 деп алып,
деп алып,
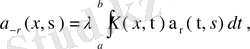
теңдігін аламыз, яғни теорема орынды.
Егер жоғарыдағы (61) теңдеуіне түйіндес
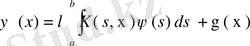
теңдеуіне Фредгольм әдісін толығымен қайталасақ, оның да шешімін
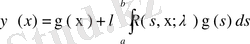
түрінде анықтаймыз, мұндағы
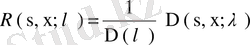 .
.
Бұдан бөлшектің бөлімінде Фредгольм анықтауышы
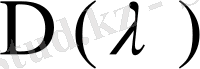 алымында х пен s- тің орындары ауысқан
алымында х пен s- тің орындары ауысқан
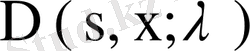 анықтауышы тұрғанын байқаймыз. Сондықтан түйіндес теңдеу мен жоғарыдағы (61) теңдеуінің меншікті сандары ортақ. Демек мына тұжырым орынды.
анықтауышы тұрғанын байқаймыз. Сондықтан түйіндес теңдеу мен жоғарыдағы (61) теңдеуінің меншікті сандары ортақ. Демек мына тұжырым орынды.
- теорема. Біртекті (62) интегралдық теңдеуі мен оған түйіндес
(63)
теңдеуі пара- пар (олардың бірдей шешімдері бар болады немесе екеуінің де шешімі жоқ болады) .
Ескерту. Егер біртекті интегралдық теңдеу нольдік емес бір
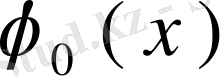 шешімі бар болса, онда ол теңдеудің ақырсыз көп нольдік емес шешімдері бар болады, себебі
шешімі бар болса, онда ол теңдеудің ақырсыз көп нольдік емес шешімдері бар болады, себебі
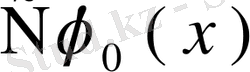 те сол теңдеудің шешімі болады мұнда С- кез келген тұрақты шама.
те сол теңдеудің шешімі болады мұнда С- кез келген тұрақты шама.
Біртекті интегралдық теңдеудің меншікті мәні λ санына сәйкес сызықты тәуелсіз шешімдерінің саны ол мәннің рангі деп аталады. λ меншікті мән болсын, ал
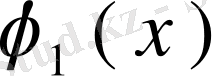 ,
,
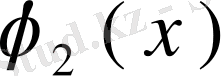 , . . . ,
, . . . ,
 функциялары сол меншікті мәнге сәйкес сызықты тәуелсіз меншікті функциялар болсын, яғни (62) теңдеуінің λ- ға сәйкес нольдік емес шешімдері былай жазылсын:
функциялары сол меншікті мәнге сәйкес сызықты тәуелсіз меншікті функциялар болсын, яғни (62) теңдеуінің λ- ға сәйкес нольдік емес шешімдері былай жазылсын:
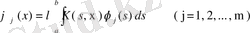 .
.
Меншікті функциялардан тұрақты коэффициенттер арқылы түзілген сызықты комбинация да меншікті функция болғандықтан, бұл функцияларға ортогональдау процесін қолдануға болады. Демек, меншікті функцияларды өзара ортогональ және нормаланған деп айтуға болады.
Соңғы теңдікті
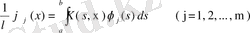
түрінде көшіріп жазайық. Міне бұл өрнектің сол жағы
 - тің ортонормаланған меншікті функциялар системасы бойынша түзілген Фурье коэффицинті екенін көреміз. Бессель теңсіздігі бойынша
- тің ортонормаланған меншікті функциялар системасы бойынша түзілген Фурье коэффицинті екенін көреміз. Бессель теңсіздігі бойынша
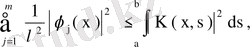
ал бұл өрнектің екі жағын х бойынша a- дан b- ға дейін интегралдап,
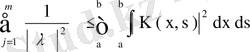
теңсіздігін, одан кейін
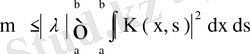
өрнегін аламыз. Бұл теңсіздік
 меншікті санына сәйкес сызықты тәуелсіз функциялар саны m соңғы теңсіздіктің оң жағынан (ақырлы саннан) аспайтынын көрсетеді. Нәтижеде мына тұжырым орынды.
меншікті санына сәйкес сызықты тәуелсіз функциялар саны m соңғы теңсіздіктің оң жағынан (ақырлы саннан) аспайтынын көрсетеді. Нәтижеде мына тұжырым орынды.
- теорема. Кез келген меншікті мәнге сәйкес сызықты тәуелсіз функциялар саны ақырлы, яғни кез келген меншікті санның рангі шектелген.
- теорема. Фредгольмнің 2- теоремасы Біртекті (62) интегралдық теңдеуі мен оған түйіндес теңдеулердің сандары бірдей сызықты тәуелсіз шешімдері бар болады; яғни ортақ меншікті сандардың рангілері бірдей.
Дәлелдеуі. Теореманы қарсы жорып дәлелдейік. (62) теңдеуінің меншікті мәні
 - ның рангі m, ал (63) теңдеуіндегі меншікті мәннің рангі
- ның рангі m, ал (63) теңдеуіндегі меншікті мәннің рангі
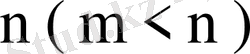 болсын.
болсын.
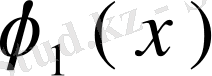 ,
,
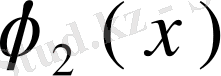 , . . . ,
, . . . ,
 және
және
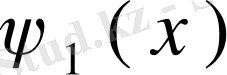
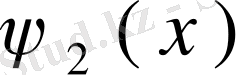 , . . . ,
, . . . ,
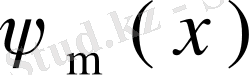 функциялары сәйкес түрде (62) және (63) теңдеулерінің сызықты тәуелсіз шешімдері делік. Жоғарыда айтқандай, бұл жерде де ол шешімдерді ортонормаланған деп аламыз.
функциялары сәйкес түрде (62) және (63) теңдеулерінің сызықты тәуелсіз шешімдері делік. Жоғарыда айтқандай, бұл жерде де ол шешімдерді ортонормаланған деп аламыз.
Жаңадан ядро түзейік
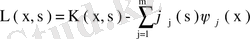 (64)
(64)
және мына екі өзара түйіндес теңдеулерді жазайық:
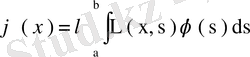 ,
,
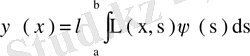 .
.
(64) ядросына байланысты бұл теңдеулерді
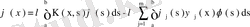 , (65)
, (65)
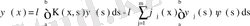 (66)
(66)
түрінде жазайық.
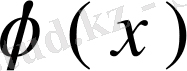 функциясы (65) теңдеуінің шешімі болсын. Теңдеудің екі жағын да
функциясы (65) теңдеуінің шешімі болсын. Теңдеудің екі жағын да
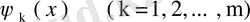 функциясына көбейтіп, нәтижелерді х бойынша a- дан b- ға дейін интегралдап, келесі теңдеуді аламыз:
функциясына көбейтіп, нәтижелерді х бойынша a- дан b- ға дейін интегралдап, келесі теңдеуді аламыз:
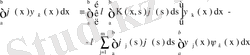
Егер біз
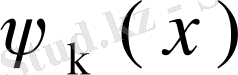 функциялары
функциялары
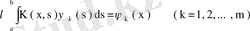
теңдеулерінің шешімдері екенін және олардың ортонормаланғанын еске алсақ, алдыңғы теңдеуді
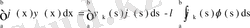
түрінде жазамыз. Бұдан
 екенін ескеріп,
екенін ескеріп,
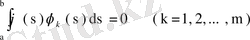 (67)
(67)
өрнегін аламыз. Демек, (67) шарттарын пайдаланып, (65) теңдеуін
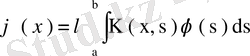
түрінде жазамыз. Бұдан біз (65) теңдеуінің кез келген шешімі (62) теңдеуін де қанағаттандыратынын көреміз. Олай болса,
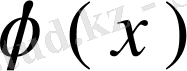 шешімі сызықты тәуелсіз шешімдердің сызықты комбинациясы ретінде, яғни
шешімі сызықты тәуелсіз шешімдердің сызықты комбинациясы ретінде, яғни
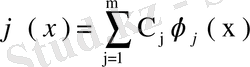
түрінде өрнектеледі екен.
Енді барлық
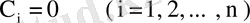 екенін көрсетейік. Ол үшін теңдіктің екі жағында
екенін көрсетейік. Ол үшін теңдіктің екі жағында
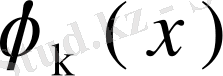 - ке көбейтіп, нәтижені х бойынша a- дан b- ға дейін интегралдап,
- ке көбейтіп, нәтижені х бойынша a- дан b- ға дейін интегралдап,
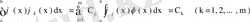
қатысын аламыз. Бұдан (67) өрнектерін ескеріп,
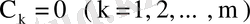 екенін шығарамыз. Сонымен
екенін шығарамыз. Сонымен
 , яғни біртекті теңдеудің тек нольдік шешімі ғана бар болатынын көреміз.
, яғни біртекті теңдеудің тек нольдік шешімі ғана бар болатынын көреміз.
Енді түйіндес теңдеудің нольге тең емес шешімі бар болатынын көрсетейік. (66) теңдеуінде
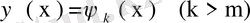 деп алып және
деп алып және
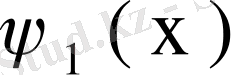 ,
,
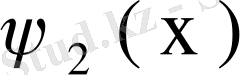 , . . . ,
, . . . ,
 - ортогональ функциялар системасы екенін ескеріп, оның үстіне
- ортогональ функциялар системасы екенін ескеріп, оның үстіне
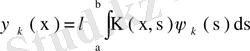
екнін пайдаланып,
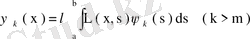
теңдігін аламыз, яғни
 түйіндес теңдеудің шешімі. Демек, нәтижеде 3- теоремаға қайшы тұжырымға келеміз. Бұл қайшылық
түйіндес теңдеудің шешімі. Демек, нәтижеде 3- теоремаға қайшы тұжырымға келеміз. Бұл қайшылық
 болуы мүмкін еместігін көрсетеді. Дәл осылай
болуы мүмкін еместігін көрсетеді. Дәл осылай
 жағдайының да мүмкін болмайтынын дәлелдей аламыз. Сондықтан
жағдайының да мүмкін болмайтынын дәлелдей аламыз. Сондықтан
 , демек, Фредгольмнің 2- теоремасы дәлелденді.
, демек, Фредгольмнің 2- теоремасы дәлелденді.
Енді
 ядроның меншікті мәні болған жағдайда біртекті емес (61) теңдеуін зерттейміз. (61) теңдеуінің шешімі бар, ол
ядроның меншікті мәні болған жағдайда біртекті емес (61) теңдеуін зерттейміз. (61) теңдеуінің шешімі бар, ол
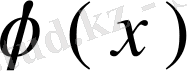 деп қабылдайық. Теңдеудің екі жағын да сәйкес түйіндес теңдеудің меншікті функциялары
деп қабылдайық. Теңдеудің екі жағын да сәйкес түйіндес теңдеудің меншікті функциялары
 - ке көбейтіп, одан кейін х бойынша a- дан b- ға дейін интегралдап,
- ке көбейтіп, одан кейін х бойынша a- дан b- ға дейін интегралдап,
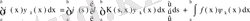
өрнегін аламыз. Бұл жерде (63) теңдеуін пайдалансақ,
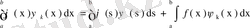 ,
,
бұдан
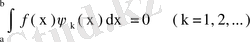 (68)
(68)
шығады. Демек (61) теңдеуінің шешілуі үшін
 функциясы (68) шартын қанағаттандыруы қажет, бұл шарттағы
функциясы (68) шартын қанағаттандыруы қажет, бұл шарттағы
 түйіндес функцияның
түйіндес функцияның
 меншікті мәніне сәйкес меншікті функциялар. Енді осы (68) шарттарының жеткілікті де болатынын көрсетейік. (68) шарты орынды деп қабылдайық.
меншікті мәніне сәйкес меншікті функциялар. Енді осы (68) шарттарының жеткілікті де болатынын көрсетейік. (68) шарты орынды деп қабылдайық.
 ядросын (64) формуласы бойынша түземіз.
ядросын (64) формуласы бойынша түземіз.
Біз жоғарыда
 саны бұл ядроның меншікті мәні емес екенін көрдік, демек
саны бұл ядроның меншікті мәні емес екенін көрдік, демек
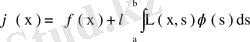 (69)
(69)
теңдеуінің шешуі бар. Бұл теңдеуді мына
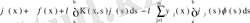
түрде жазып, оның екі жағын да
 функциясына көбейтіп, одан кейін х бойынша a- дан b- ға дейін интегралдап,
функциясына көбейтіп, одан кейін х бойынша a- дан b- ға дейін интегралдап,
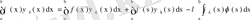
өрнегін аламыз. Бұдан (68) шартын пайдаланып,
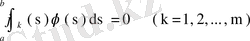
екенін көреміз.
Сонымен (69) теңдеуі (61) теңдеуіне келтірілді, яғни (69) теңдеуінің шешімі
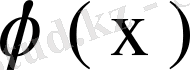 (61) теңдеуінің де шешімі екен. Демек (68) шарттары жеткілікті екенін дәлелдедік. Егер осы шарттар орындалса, онда біртекті емес (61) теңдеуінің жалпы шешімі қандай да бір дербес
(61) теңдеуінің де шешімі екен. Демек (68) шарттары жеткілікті екенін дәлелдедік. Егер осы шарттар орындалса, онда біртекті емес (61) теңдеуінің жалпы шешімі қандай да бір дербес
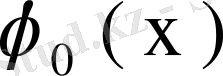 шешімі мен біртекті теңдеудің жалпы шешімінің қосындысынан тұрады:
шешімі мен біртекті теңдеудің жалпы шешімінің қосындысынан тұрады:
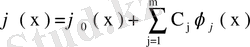 ,
,
мұндағы
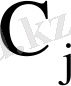 - тұрақты шамалар. Сөйтіп, бұл жағдайда (61) теңдеуінің ақырсыз көп шешімдері бар болады. Дербес
- тұрақты шамалар. Сөйтіп, бұл жағдайда (61) теңдеуінің ақырсыз көп шешімдері бар болады. Дербес
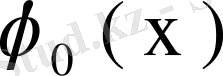 шешімін
шешімін
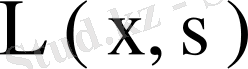 ядросының резольвентасы арқылы анықтайды.
ядросының резольвентасы арқылы анықтайды.
Міне бұл талқылаулар нәтижесінде мына тұжырымды дәлелдедік.
- теорема. Фредгольмнің теоремасы. Егер(61) теңдеуінің меншікті мәні болса, онда ол теңдеудің шешілуі үшін сол теңдеудегібос мүшесі (68) шартын қанағаттандыруы қажетті де жеткілікті. (68) (61) теңдеуіне түйіндес біртекті теңдеудің меншікті функциялары. Егер (68) шарттар орындалса, онда (61) теңдеуінің ақырсыз көп жиынды шешімі бар болады да олар соңғы формуламен өрнектеледі.
Сонымен дәлелденген теоремаларды былай қорытындылауға болады.
1. Егер Фредгольмнің біртекті интегралдық теңдеуінің тек нольдік шешімі ғана бар болса, онда оған сәйкес біртекті емес интегралдық теңдеудің кез келген бос мүше
 үшін жалғыз ғана шешімі бар болады.
үшін жалғыз ғана шешімі бар болады.
- Берілген біртекті интегралдық теңдеу мен оның түйіндес интегралдық теңдеуінің шешімдері бірдей нольге тең немесе нольге тең емес болады. Бұған қоса олардың меншікті мәндерінің рангтері бірдей болады.
- Біртекті интегралдық теңдеудің нольге тең емес шешімдері бар болған жағдайда, біртекті емес интегралдық теңдеудің шешімі бар болуы үшін оның бос мүшесі түйіндес интегралдық теңдеудің меншікті функцияларымен ортогональ болуы қажетті де жеткілікті.
- СИММЕТРИЯЛЫҚ ИНТЕГРАЛДЫҚ ТЕҢДЕУЛЕРСимметриялық ядролар және олардың кейбір қасиеттері
кеңістігінде
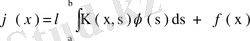
интегралдық теңдеуін қарастырайық. Егер нақты ядро
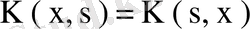 шартын қанағаттандырса, оны симметриялық ядро деп атайды. Мысалы,
шартын қанағаттандырса, оны симметриялық ядро деп атайды. Мысалы,
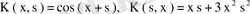
симметриялық ядролар. Комплекстік
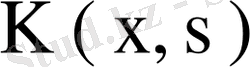 ядросы
ядросы
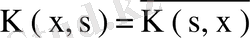 шартын қанағаттандырса, оны симметриялық эрмиттік ядро деп атайды. Ядросы симметриялық ядро болатын интегралдық теңдеуді симметриялық интегралдық теңдеу деп айтады.
шартын қанағаттандырса, оны симметриялық эрмиттік ядро деп атайды. Ядросы симметриялық ядро болатын интегралдық теңдеуді симметриялық интегралдық теңдеу деп айтады.
Егер
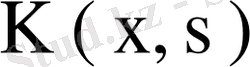 симметриялық (эрмиттік) ядро болса, онда бұл ядроның қайталанған ядролары симметриялық болады. Расында, қайталанған ядро анықтамасы бойынша
симметриялық (эрмиттік) ядро болса, онда бұл ядроның қайталанған ядролары симметриялық болады. Расында, қайталанған ядро анықтамасы бойынша
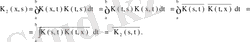
Дәл осылай жалпы жағдай үшін де бұл қасиеттің орынды екенін оңай көруге болады.
Егер
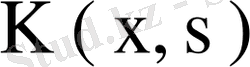 симметриялық эрмиттік ядро болса, онда Фредгольм орераторы
симметриялық эрмиттік ядро болса, онда Фредгольм орераторы
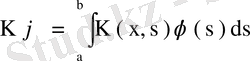
өзіне түйіндес, яғни
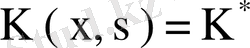 болады. Расында
болады. Расында
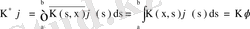 .
.
Біз бұдан былай нақты аргументті симметриялық ядроларды қарастырамыз.
- Симметриялық ядролы интегралдық теңдеулердің негізгі қасиеттері
1-теорема. Симметриялық ядролы интегралдық теңдеулердің әр түрлі меншікті мәндеріне сәкес меншікті функциялар өзара ортогональ.
Дәлелдеуі. Симметриялық
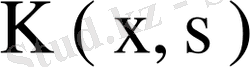 ядроның меншікті мәндері
ядроның меншікті мәндері
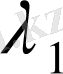 мен
мен
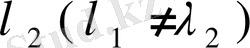 , ал
, ал
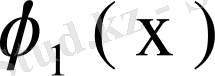 пен
пен
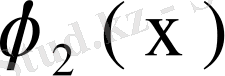 оларға сәйкес меншікті функциялар болсын. Сонда
оларға сәйкес меншікті функциялар болсын. Сонда
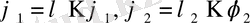 теңдеулері орынды. Бірінші теңдеуді
теңдеулері орынды. Бірінші теңдеуді
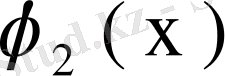 , ал екіншіні
, ал екіншіні
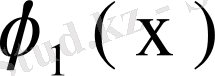 функциясына көбейткеннен соң олардың айырымын интегралдап, мына теңдікті аламыз:
функциясына көбейткеннен соң олардың айырымын интегралдап, мына теңдікті аламыз:
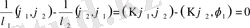
немесе
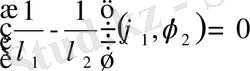 .
.
Бұл теңідеуде
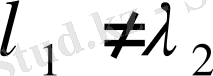 болғандықтан, ол тек
болғандықтан, ол тек
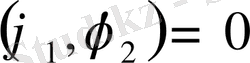 болған жағдайда ғана орынды. Теорема дәлелденді.
болған жағдайда ғана орынды. Теорема дәлелденді.
2- теорема. Симметриялық ядроның меншікті мәндері нақты сандар болады.
Дәлелдеуі. Меншікті
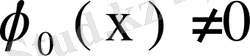 функциясына сәйкес меншікті мән
функциясына сәйкес меншікті мән
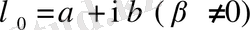 - комплекс сан деп ұйғарайық. Сонда
- комплекс сан деп ұйғарайық. Сонда
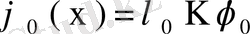 теңдігі орынды.
теңдігі орынды.
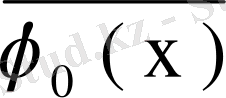 меншікті функциясының меншікті мәні
меншікті функциясының меншікті мәні
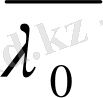 болатынын, яғни
болатынын, яғни
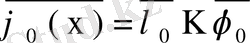 теңдігі орынды екенін оңай байқауға болады. 1- теоремадан
теңдігі орынды екенін оңай байқауға болады. 1- теоремадан
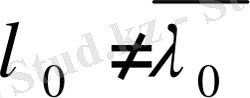 болғандықтан,
болғандықтан,
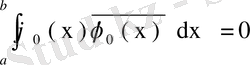 , демек
, демек
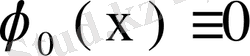 . Сонымен
. Сонымен
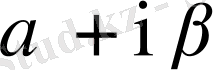 саны
саны
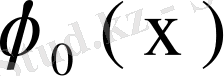 функциясының меншікті мәні бола алмайды.
функциясының меншікті мәні бола алмайды.
Ескерту. Меншікті функцияларды әрбірінің нормасына бөліп нормалауға болады. Одан кейін, егер бір меншікті мәнге бірнеше сызықты тәуелсіз меншікті функциялар сәйкес келсе, онда оларды Шмидтің ортогональдау әдісін қолданып, өзара ортогоналдауға және нормалауға болады. 1- теоремадан әр түрлі меншікті мәндерге сәйкес меншікті функциялар өзара ортогональ екенін көргенбіз.
Демек, симметриялық ядроның меншікті функциялары жиынын ортонормаланған система деп есептеуге болады. Бұдан былай, бір меншікті мәнге бірнеше сызықты тәуелсіз меншікті функциялар сәйкес келетін жағдайда, меншікті мәндер тізбегін жазарда, сол меншікті мәнге қанша меншікті функция сәйкес келсе, сонша қайталап жазамыз. Бұдан кейін әрбір меншікті мәнге жалғыз меншікті функция сай келеді деп айта аламыз. Сонымен қатар келешекте меншікті мәндерді абсолют шамалары бойынша өсетіндей етіп реттеп жазамыз.
Егер меншікті мәндер ақырсыз көп болса, онда Фредгольм теоремасы бойынша олардың шексіздікте шектік нүктелері болуы мүмкін, сондықтан,
 жағдайда
жағдайда
 болады.
болады.
- лемма. Екінші қайталанған ядроның меншікті мәндері жиыны сол ядроның меншікті мәндерінің квадраттарының жиынынан тұрады.
Дәлелдеуі.
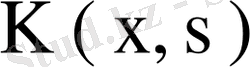 ядросының меншікті мәні
ядросының меншікті мәні
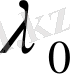 - ге сәйкес меншікті функциясы
- ге сәйкес меншікті функциясы
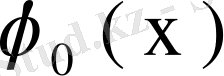 болсын, сонда
болсын, сонда
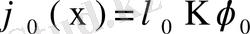 теңдігі орынды. Бұл теңдікке
теңдігі орынды. Бұл теңдікке
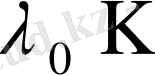 операторын қолданып,
операторын қолданып,
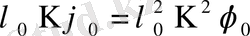 теңдеуін аламыз. Одан кейін осы теңдеулерден
теңдеуін аламыз. Одан кейін осы теңдеулерден
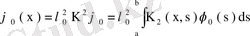
теңдеуі шығады. Бұл соңғы теңдеуден
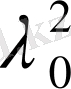 саны -
саны -
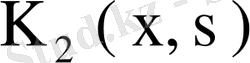 ядросының
ядросының
 меншікті функциясын сәйкес меншікті мәні екенін көреміз.
меншікті функциясын сәйкес меншікті мәні екенін көреміз.
Екінші жағынан
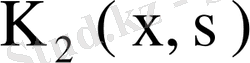 ядросының меншікті мәні
ядросының меншікті мәні
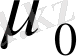 ал
ал
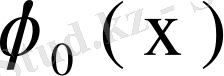 оған сәйкес меншікті функциясы болсын, яғни
оған сәйкес меншікті функциясы болсын, яғни
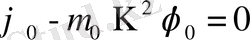 шарты орындалсын. Бұл соңғы теңдеуді
шарты орындалсын. Бұл соңғы теңдеуді
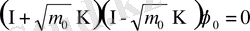 (70)
(70)
түрінде жазып және
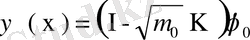 деп белгілейік. Мұнда
деп белгілейік. Мұнда
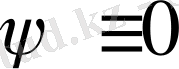 болуы мүмкін. Бұл жағдайда да дәлелденді.
болуы мүмкін. Бұл жағдайда да дәлелденді.
- лемманың салдары. Егерсимметриялық ядро болса, онда қайталанушы ядроның меншікті мәндері оң.
Ескерту. Дәл осылай қайталанған
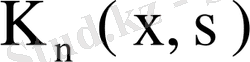 ядросының меншікті мәндерінің жиынына
ядросының меншікті мәндерінің жиынына
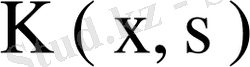 ядросының n- дәрежелі меншікті мәндері жиыны дәл келеді.
ядросының n- дәрежелі меншікті мәндері жиыны дәл келеді.
3-теорема. Кез келген симметриялық ядроның кемінде бір меншікті мәні бар болады.
Дәлелдеуі. Қайталанған
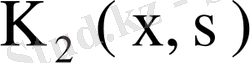 ядросының кемінде бір меншікті мәні бар екенін дәлелдейік, онда жоғарыда лемма бойынша
ядросының кемінде бір меншікті мәні бар екенін дәлелдейік, онда жоғарыда лемма бойынша
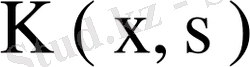 - тың да меншікті мәні бар болады.
- тың да меншікті мәні бар болады.
Қайталанған ядро
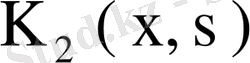 - тың
- тың
 жазықтығының
жазықтығының
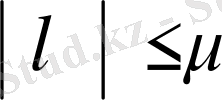 болатындай облысында меншікті мәні жоқ болсын (мұндағы
болатындай облысында меншікті мәні жоқ болсын (мұндағы
 - кез келген оң сан) . Кез келген
- кез келген оң сан) . Кез келген
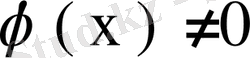 функциясын алып, жаңадан
функциясын алып, жаңадан
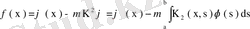 (71)
(71)
функциясын құрамыз. Әрине,
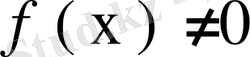 . Қарсы жағдайда, яғни
. Қарсы жағдайда, яғни
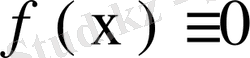 болса,
болса,
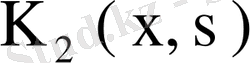 ядросының меншікті мәні
ядросының меншікті мәні
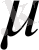 болар еді де теорема дәлелденген болар еді. Сондықтан (71) теңдеуін бос мүшесі
болар еді де теорема дәлелденген болар еді. Сондықтан (71) теңдеуін бос мүшесі
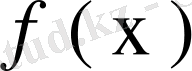 ал белгісіз функция
ал белгісіз функция
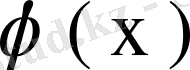 болған 2- текті интегралдық теңдеу ретінде қарастырамыз. Бұл теңдеудің шешімі
болған 2- текті интегралдық теңдеу ретінде қарастырамыз. Бұл теңдеудің шешімі
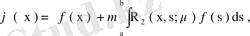
мұндағы
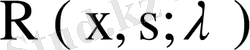 жоғарыдағы (71) теңдеудегі
жоғарыдағы (71) теңдеудегі
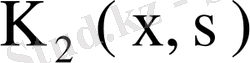 ядросының резольвентасы. Бұл теңдіктің екі жағын да
ядросының резольвентасы. Бұл теңдіктің екі жағын да
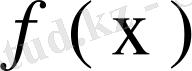 функциясына скаляр көбейтсек,
функциясына скаляр көбейтсек,
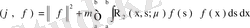 (72)
(72)
теңдігі шығады. Жоғарыда біз
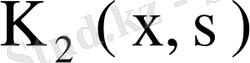 ядросының
ядросының
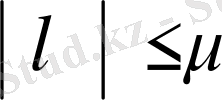 дөңгелегі ішінде меншікті мәні жоқ деп ұйғардық, олай болса,
дөңгелегі ішінде меншікті мәні жоқ деп ұйғардық, олай болса,
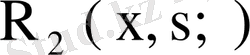 резольвентасы
резольвентасы
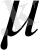 - ға қатысты бүтін функция, яғни оны
- ға қатысты бүтін функция, яғни оны
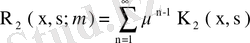
түрінде өрнектеуге болады. Бұл жағдайда (72) теңдігіндегі интеграл былай жазылады:
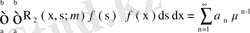 ,
,
мұндағы
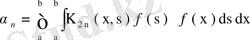 .
.
Енді осы
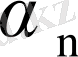 оң сан екенін көрсетейік. Соңғы өрнектен
оң сан екенін көрсетейік. Соңғы өрнектен
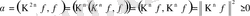 .
.
Олай болса, (72) теңдігінен
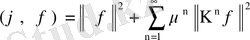
және бұдан
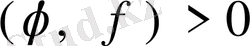 екені шығады., демек (71) теңдігінен
екені шығады., демек (71) теңдігінен
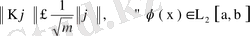 (73)
(73)
Енді
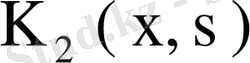 ядросының ешқандай меншікті мәні жоқ деп ұйғарайық. Бұл жағдайда
ядросының ешқандай меншікті мәні жоқ деп ұйғарайық. Бұл жағдайда
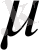 санын жеткілікті мөлшерде үлкен етіп, яғни
санын жеткілікті мөлшерде үлкен етіп, яғни
 деп алуға болады. Олай болса, (73) теңсіздігінен
деп алуға болады. Олай болса, (73) теңсіздігінен
 , яғни
, яғни
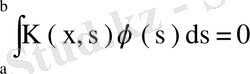 болады. Бұндай кезде
болады. Бұндай кезде
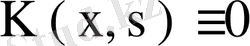 екенін дәлелдеу қиын емес. Расында, х- ті тұрақтылап,
екенін дәлелдеу қиын емес. Расында, х- ті тұрақтылап,
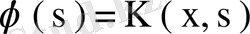 деп алсақ,
деп алсақ,
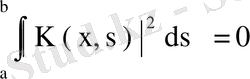
екені шығады, яғни
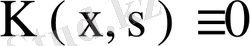 . Сонымен егер
. Сонымен егер
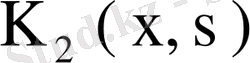 ядросының бірде- бір меншікті мәні жоқ болса, онда
ядросының бірде- бір меншікті мәні жоқ болса, онда
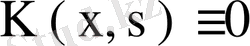 екен. Демек, егер
екен. Демек, егер
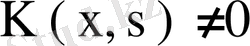 болса, онда
болса, онда
 қайталанушы ядросының кемінде бір меншікті мәні бар болады. 3- теорема дәлелденді.
қайталанушы ядросының кемінде бір меншікті мәні бар болады. 3- теорема дәлелденді.
Ескерту. (73) теңсіздігі
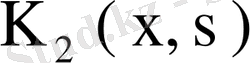 ядросының меншікті мәні жоқ болатын
ядросының меншікті мәні жоқ болатын
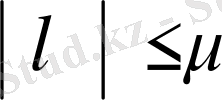 дөңгелегі ішінде орынды, басқаша айтқанда ол
дөңгелегі ішінде орынды, басқаша айтқанда ол
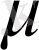 саны
саны
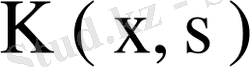 ядросының ең кіші меншікті мәнінен аз болғанда қанағаттанады.
ядросының ең кіші меншікті мәнінен аз болғанда қанағаттанады.
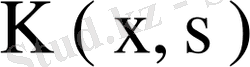 ядросының модуль шамасы бойынша ең кіші меншікті мәні
ядросының модуль шамасы бойынша ең кіші меншікті мәні
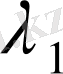 болсын, сонда
болсын, сонда
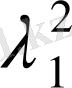 саны
саны
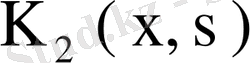 ядросының меншікті мәні болады. Егер
ядросының меншікті мәні болады. Егер
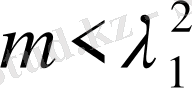 болса, (73) теңсіздігі орынды. Сол (73) теңсіздігінен
болса, (73) теңсіздігі орынды. Сол (73) теңсіздігінен
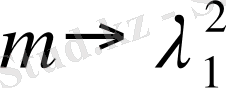 болғанда
болғанда
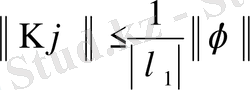 .
.
Бұл теңсіздікте теңдік қатысы
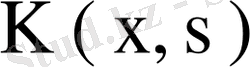 ядросының
ядросының
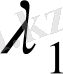 меншікті мәніне сәйкес
меншікті мәніне сәйкес
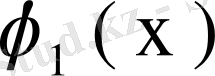 меншікті функциясы үшін орындалады. Расында, бұл жағдайда
меншікті функциясы үшін орындалады. Расында, бұл жағдайда
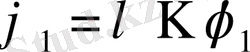 . Бұдан
. Бұдан
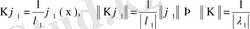 .
.
4- теорема. Егер
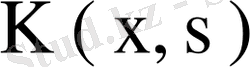 симметриялық ядро болса, онда оның меншікті мәні сол ядро резольвентасының қарапайым полюсі болады.
симметриялық ядро болса, онда оның меншікті мәні сол ядро резольвентасының қарапайым полюсі болады.
Дәлелдеуі. Қарсы жориық, яғни
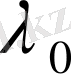 меншікті мән
меншікті мән
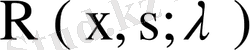 резольвентасының
резольвентасының
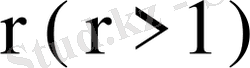 ретті полюсі болсын. Онда
ретті полюсі болсын. Онда
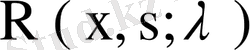 Лоран қатарына жіктеледі.
Лоран қатарына жіктеледі.
 (74)
(74)
мұндағы
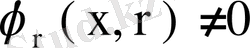 . Резольвента мына интегралдық теңдеуді қанағаттандырады:
. Резольвента мына интегралдық теңдеуді қанағаттандырады:
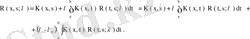
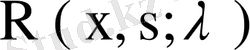 орнына (74) теңдігінің оң жағын қойып, одан кейін алынған өрнектің екі жағындағы көпмүшеліктердегі
орнына (74) теңдігінің оң жағын қойып, одан кейін алынған өрнектің екі жағындағы көпмүшеліктердегі
 айырымы коэффициенттерін теңестіріп,
айырымы коэффициенттерін теңестіріп,
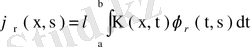 ,
,
 (75)
(75)
теңдіктерін аламыз. Бұл теңдіктердің біріншісін
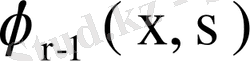 - ке, ал екіншісін -
- ке, ал екіншісін -
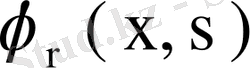 - ке көбейтіп, одан кейін алынған нәтижелерді қоссақ,
- ке көбейтіп, одан кейін алынған нәтижелерді қоссақ,
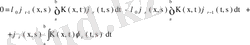
теңдігі шығады. Мұны х бойынша a- дан b- ға дейін интегралдасақ және ядроның симметриялығын пайдалансақ, онда
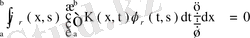 ,
,
одан кейін бұл өрнекке (75) теңдігін қолдансақ,
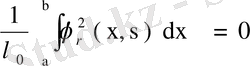
немесе барлық жерде дерлік
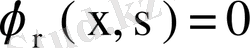 екені шығады. Демек,
екені шығады. Демек,
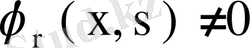 деген шартқа кері қорытынды алдық. Міне бұл қайшылық теореманың орынды екенін дәлелдейді.
деген шартқа кері қорытынды алдық. Міне бұл қайшылық теореманың орынды екенін дәлелдейді.
5- теорема. әрбір шектелген интервалда
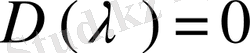 теңдеуінің ақырлы санды түбірлері бар болады.
теңдеуінің ақырлы санды түбірлері бар болады.
Дәлелдеуі. Қарсы жориық, яғни
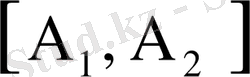 кесіндісінде
кесіндісінде
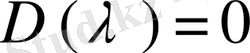 теңдеуінің ақырсыз көп түбірлері жиыны
теңдеуінің ақырсыз көп түбірлері жиыны
 бар деп ұйғарайық. Әрбір
бар деп ұйғарайық. Әрбір
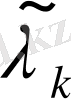 түбірлеріне
түбірлеріне
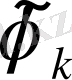 меншікті функциясы сәйкес келетіні, олардың
меншікті функциясы сәйкес келетіні, олардың
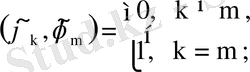
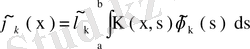
шарттарын қанағаттандыратыны белгілі. Соңғы теңдіктен
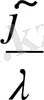 өрнегі
өрнегі
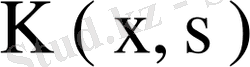 ядросының
ядросының
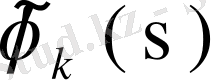 ортонормаланған системасы бойынша Фурье коэффициенттрі екенін көреміз. Бессель теңсіздігін пайдаланып
ортонормаланған системасы бойынша Фурье коэффициенттрі екенін көреміз. Бессель теңсіздігін пайдаланып
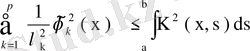
теңсіздігін аламыз. Бұны х бойынша a- дан b- ға дейін интегралдасақ,
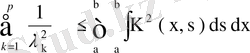 .
.
Ал
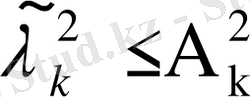 болғандықтан, соңғы теңсіздіктер
болғандықтан, соңғы теңсіздіктер
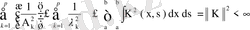 .
.
Егер
 болса, соңғы теңсіздіктің сол жағы кез келген шамадан үлкен бола алады, сондықтан бұл теңсіздік орындалмайды. Міне бұл қайшылық теореманы дәлелдейді.
болса, соңғы теңсіздіктің сол жағы кез келген шамадан үлкен бола алады, сондықтан бұл теңсіздік орындалмайды. Міне бұл қайшылық теореманы дәлелдейді.
- Ядроны қатарға жіктеу
Симметриялық
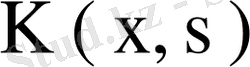 ядросын қарастырайық. Оның меншікті мәндері
ядросын қарастырайық. Оның меншікті мәндері
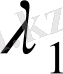 ,
,
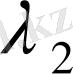 , . . . ,
, . . . ,
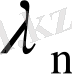 , . . . , ал меншікті функциялары
, . . . , ал меншікті функциялары
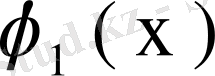 ,
,
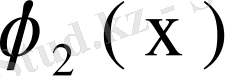 , . . . ,
, . . . ,
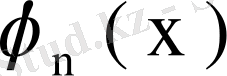 , . . . болсын. Меншікті функциялар ортонормаланған, ал меншікті мәндер абсолют шамаларының өсу ретімен орналасқан болсын. Жаңадан
, . . . болсын. Меншікті функциялар ортонормаланған, ал меншікті мәндер абсолют шамаларының өсу ретімен орналасқан болсын. Жаңадан
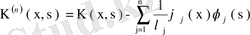 (76)
(76)
симметриялық ядросын құрайық.
4- лемма.
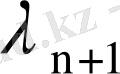 ,
,
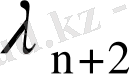 , . . . ,
, . . . ,
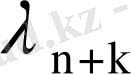 , . . . ;
, . . . ;
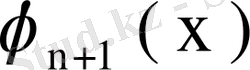 ,
,
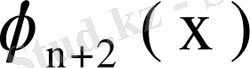 , . . . ,
, . . . ,
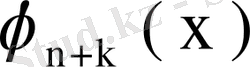 , . . . тізбектері симметриялық
, . . . тізбектері симметриялық
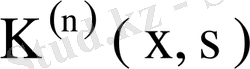 ядросының меншікті мәндері мен оларға сәйкес меншікті функциялары болады.
ядросының меншікті мәндері мен оларға сәйкес меншікті функциялары болады.
Дәлелдеуі.
 болсын. Бірінші тізбектен
болсын. Бірінші тізбектен
 - ді, ал екінші тізбектен оған сәйкес келуші
- ді, ал екінші тізбектен оған сәйкес келуші
 функциясын алып,
функциясын алып,
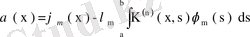
өрнегін құрайық. Енді
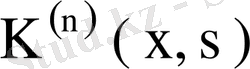 ядросын (76) өрнегімен ауыстырып мынадай теңдік аламыз:
ядросын (76) өрнегімен ауыстырып мынадай теңдік аламыз:
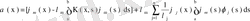 .
.
Бұндағы
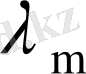 мен
мен

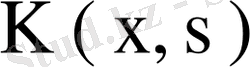 ядросының меншікті мәні мен меншікті функциясы болғандықтан, квадрат жақшадағы өрнек нольге тең және
ядросының меншікті мәні мен меншікті функциясы болғандықтан, квадрат жақшадағы өрнек нольге тең және
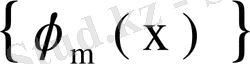 функциялары системасы ортонормаланғандықтан,
функциялары системасы ортонормаланғандықтан,
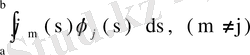
Демек,
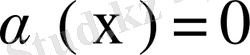 , яғни
, яғни
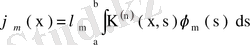 , олай болса,
, олай болса,
 жағдайында
жағдайында
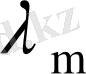 мен
мен
 -
-
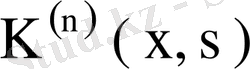 ядросының меншікті мәні мен меншікті функциясы.
ядросының меншікті мәні мен меншікті функциясы.
Керісінше, егер
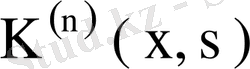 ядросы үшін
ядросы үшін
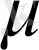 саны мен
саны мен
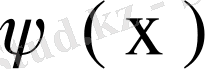 функциясы меншікті мән мен меншікті функция болса, онда олар
функциясы меншікті мән мен меншікті функция болса, онда олар
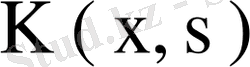 ядросының меншікті мәндері мен меншікті функцияларының жиындарынан табылады. Ұйғарым бойынша
ядросының меншікті мәндері мен меншікті функцияларының жиындарынан табылады. Ұйғарым бойынша
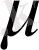 мен
мен
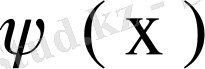
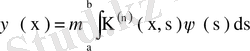
теңдеуін қанағаттандырады. Бұл теңдіктегі
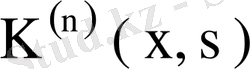 ядросын (76) өрнегі бойынша ауыстырсақ,
ядросын (76) өрнегі бойынша ауыстырсақ,
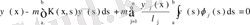 (77)
(77)
Бұл теңдеудің екі жағын да
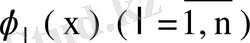 функциясына скаляр көбейтіп,
функциясына скаляр көбейтіп,
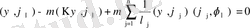
теңдеуіне келеміз.
 ядросының симметриялық және
ядросының симметриялық және
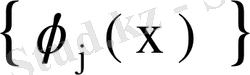 функцияларының ортонормаланған қасиетін ескерсек,
функцияларының ортонормаланған қасиетін ескерсек,
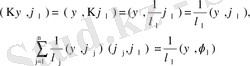
өрнектерін аламыз. Бұл жағдайда алдыңғы теңдеуден
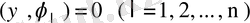 ортогоналдық шарты шығады. . онда (77) теңдеуі:
ортогоналдық шарты шығады. . онда (77) теңдеуі:
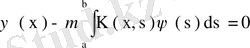
түрінде жазылады. Бұл теңдеуден
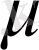 мен
мен
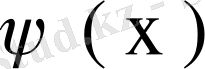 -
-
 ядросының меншікті мәні мен меншікті функциясы екенін, ал
ядросының меншікті мәні мен меншікті функциясы екенін, ал
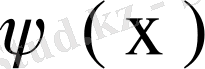 - тің
- тің
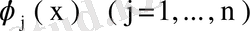 функцияларымен ортогональ болғандықтан
функцияларымен ортогональ болғандықтан
 ретті меншікті функциялардың біреуімен сай келетінін көреміз.
ретті меншікті функциялардың біреуімен сай келетінін көреміз.
Салдар. Егер
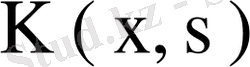 ядросының n- нен көп меншікті мәні бар болса, онда
ядросының n- нен көп меншікті мәні бар болса, онда
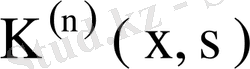 ядросының меншікті мәндерінің модулі бойынша ең кішісі
ядросының меншікті мәндерінің модулі бойынша ең кішісі
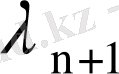 болады.
болады.
Берілген ядроның меншікті мәндері
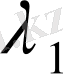 ,
,
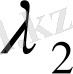 , . . . ,
, . . . ,
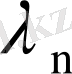 ақырлы санды болған жеке жағдайды қарастырайық. Онда
ақырлы санды болған жеке жағдайды қарастырайық. Онда
 ядросының бірде- бір меншікті мәні болмайды. Бұндай жағдайда бұрын дәлелденген теорема бойынша
ядросының бірде- бір меншікті мәні болмайды. Бұндай жағдайда бұрын дәлелденген теорема бойынша
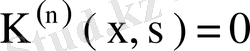 немесе
немесе
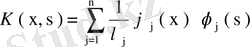 .
.
Осы формуладан
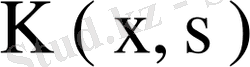 ядросының ерекшеленген ядро екенін көреміз. Кез келген ерекшеленген ядроның ақырлы санды меншікті мәндері бар болғандықтан және жоғарыдағы талдаулардан мына теорема орынды.
ядросының ерекшеленген ядро екенін көреміз. Кез келген ерекшеленген ядроның ақырлы санды меншікті мәндері бар болғандықтан және жоғарыдағы талдаулардан мына теорема орынды.
Дини теоремасы. Квадратымен интегралданатын симметриялық ядроның меншікті мәндері мен меншікті функциялары ақырлы санды болуы үшін оның ерекшеленген ядро болуы қажетті де жеткілікті.
Салдар. Кез келген квадратымен интегралданатын
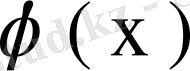 функциясы үшін
функциясы үшін
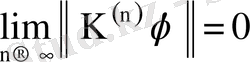
теңдігі орынды.
Дәлелдеуі. Егер
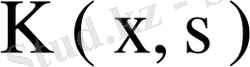 ерекшеленбеген ядро болса, соңғы теңдіктің орындалуы ап-айқын. Бірінші салдар бойынша
ерекшеленбеген ядро болса, соңғы теңдіктің орындалуы ап-айқын. Бірінші салдар бойынша
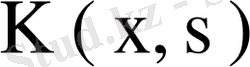 ядросы ерекшеленбеген болса, онда
ядросы ерекшеленбеген болса, онда
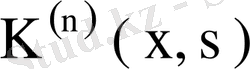 ядросының модулі бойынша ең кіші меншікті мәні
ядросының модулі бойынша ең кіші меншікті мәні
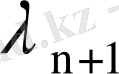 болады.
болады.
Жоғарыдағы (73) теңсіздігі бойынша
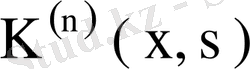 ядросы, оның меншікті мәні мен меншікті функциясы үшін
ядросы, оның меншікті мәні мен меншікті функциясы үшін
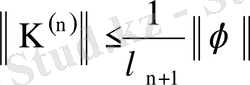
теңсіздік орынды және
 жағдайда
жағдайда
 болғандықтан соңғы өрнектен
болғандықтан соңғы өрнектен
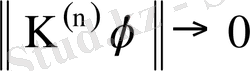 .
.
Тұрақты болған х үшін
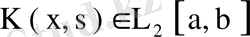 олай болса, ол ядро ортонормаланған
олай болса, ол ядро ортонормаланған
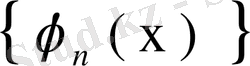 системасы бойынша
системасы бойынша
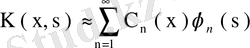
Фурье қатарына жіктеледі де, ал Фурье коэффициенттері
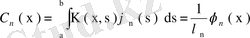
теңдігімен анықталады. Сонымен,
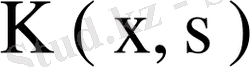 ядросына оның меншікті функциялар системасы
ядросына оның меншікті функциялар системасы
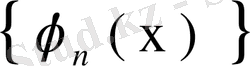 бойынша
бойынша
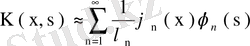
түріндегі бисызықты деп аталатын Фурье қатары сәйкес келеді екен. Бессель теңсіздігі бойынша
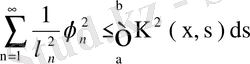 . (78)
. (78)
Бұл теңсіздіктегі қатар мүшелері оң және оларды мүшелеп х бойынша a- дан b- ға дейін интегралдап
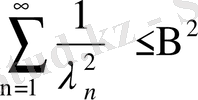 теңсіздігін аламыз, яғни
теңсіздігін аламыз, яғни
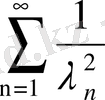 қатары жинақты.
қатары жинақты.
Енді
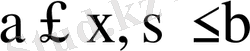 квадратында
квадратында
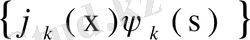 системасының ортонормаланғандығын және Рисс- Фишер теоремасын ескерсек, мынадай қорытындыға келеміз.
системасының ортонормаланғандығын және Рисс- Фишер теоремасын ескерсек, мынадай қорытындыға келеміз.
Теорема. Бисызықты қатар
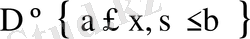 облысында орташа мағынада жинақты және ол қатардың қосындысы сол ядроға тең.
облысында орташа мағынада жинақты және ол қатардың қосындысы сол ядроға тең.
Енді қайталанған ядроларды жіктейік. Егер
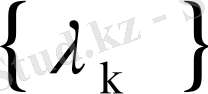 сандары мен
сандары мен
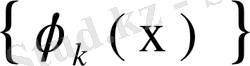 функциялары
функциялары
 симметриялық ядросының меншікті мәндері мен меншікті функциялары болса, онда
симметриялық ядросының меншікті мәндері мен меншікті функциялары болса, онда
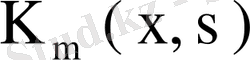 қайталанатын ядросының меншікті мәндері
қайталанатын ядросының меншікті мәндері
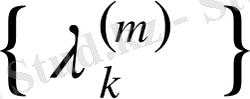 , ал меншікті функциялары
, ал меншікті функциялары
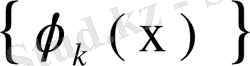 екені белгілі, яғни
екені белгілі, яғни
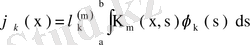 (79)
(79)
теңдігі орындалады.
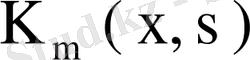 ядросын х аргументін тұрақтылап, ортонормаланған
ядросын х аргументін тұрақтылап, ортонормаланған
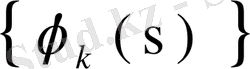 системасы бойынша Фурье қатарына жіктесек,
системасы бойынша Фурье қатарына жіктесек,
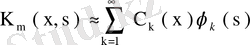 ,
,
мұндағы Фурье коэффициенттері
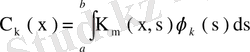
өрнегімен анықталады. Бұдан және (79) теңдігінен
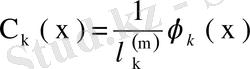 .
.
Сонымен
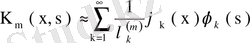 . (80)
. (80)
Егер
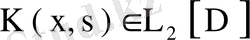 болса, онда
болса, онда
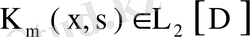 екенін көрсету қиын емес. Сондықтан (80) қатары Рисс- Фишер теоремасы бойынша орташа мағынада жинақты. Егер
екенін көрсету қиын емес. Сондықтан (80) қатары Рисс- Фишер теоремасы бойынша орташа мағынада жинақты. Егер
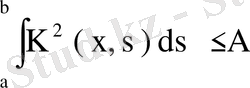 болса, онда (80) қатар тек орташа мағынада ғана жинақты емес, оның m > 2 болғанда абсолютті және бірқалыпты жинақты болатынын дәлелдеуге болады.
болса, онда (80) қатар тек орташа мағынада ғана жинақты емес, оның m > 2 болғанда абсолютті және бірқалыпты жинақты болатынын дәлелдеуге болады.
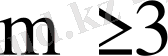 болсын.
болсын.
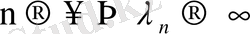 болғандықтан, n санының жеткілікті мөлшерде үлкен мәндерінде
болғандықтан, n санының жеткілікті мөлшерде үлкен мәндерінде
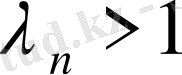 . Оларды ескеріп, (80) өрнегіне Коши- Буняковский теңсіздігін пайдалансақ,
. Оларды ескеріп, (80) өрнегіне Коши- Буняковский теңсіздігін пайдалансақ,

Жоғарыдағы (78) Бессель теңсіздігі мен соңғы теңсіздіктен
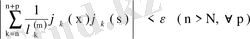
екені шығады. Олай болса, қатардың жинақтылығын көрсетуші Коши белгісі бойынша (80) қатары бірқалыпты жинақты және оның қосындысы
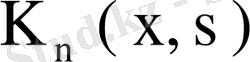 болады. Сонымен мына теорема орынды.
болады. Сонымен мына теорема орынды.
Теорема. Егер
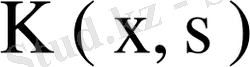 ядросы
ядросы
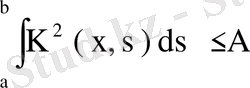 шартын қанағаттандырса, онда,
шартын қанағаттандырса, онда,
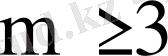 мәндерінде (80) қатары
мәндерінде (80) қатары
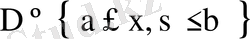 облысында абсолютті және бірқалыпты жинақты болады да
облысында абсолютті және бірқалыпты жинақты болады да
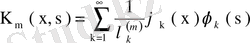 .
.
Мысал. Фредгольмнің 2- текті интегралдық
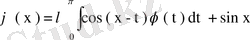
теңдеуінің шешімін табайық.
Шешуі.
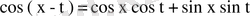 формуласын пайдалансақ теңдеуді
формуласын пайдалансақ теңдеуді
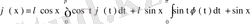
түріне келтіреміз. Бұл өрнекте
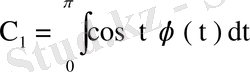 ,
,
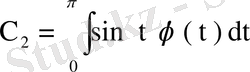
деп белгілесек, онда
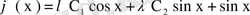 теңдеуі шығады. Бұл теңдеуде
теңдеуі шығады. Бұл теңдеуде
 мен
мен
 белгісіз тұрақты коэффициенттер. Оларды табу үшін теңдіктің екі жағын
белгісіз тұрақты коэффициенттер. Оларды табу үшін теңдіктің екі жағын
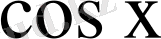 пен
пен
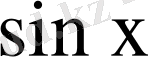 функцияларына көбейтіп, одан кейін х бойынша 0- ден
функцияларына көбейтіп, одан кейін х бойынша 0- ден
 - ге шейін интегралдап
- ге шейін интегралдап
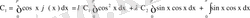 ,
,
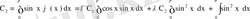
немесе
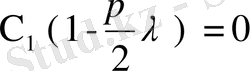 ,
,
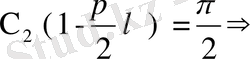
 ,
,
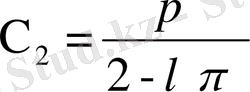 екенін табамыз. Демек, берілген теңдеудің шешімі
екенін табамыз. Демек, берілген теңдеудің шешімі
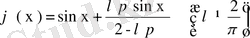
болады.
- Гильберт- Шмидт теоремасы
Егер
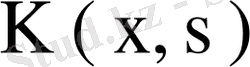 симметриялық ядросы үшін
симметриялық ядросы үшін
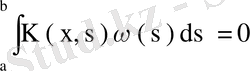 теңдігін қанағаттандыратындай
теңдігін қанағаттандыратындай
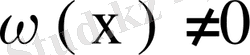 функциясы табылмаса, онда
функциясы табылмаса, онда
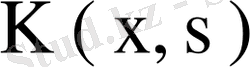 ядросы тұйық деп, ал ондай
ядросы тұйық деп, ал ондай
 функциясы табылса, онда
функциясы табылса, онда
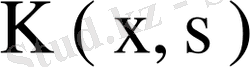 ядросы тұйық емес деп аталады.
ядросы тұйық емес деп аталады.
- теорема (Шмидт) . Меншікті функциялар системасы тұйық болуы үшін ядроның тұйық болуы қажетті де жеткілікті.
Дәлелдеуі.
тұйық емес ядро болсын, яғни
функциясы табылып,
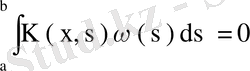
шарты орындалсын. Соңғы өрнекті
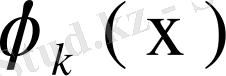 функциясына көбейтіп, сонан соң х бойынша a- дан b- ға дейін интегралдасақ,
функциясына көбейтіп, сонан соң х бойынша a- дан b- ға дейін интегралдасақ,
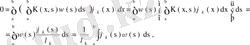
яғни
 системасы тұйық болмайды.
системасы тұйық болмайды.
Керісінше,
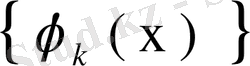 меншікті функциялар системасы тұйық болмасын, яғни
меншікті функциялар системасы тұйық болмасын, яғни
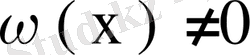 табылып, олар үшін
табылып, олар үшін
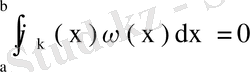 (81)
(81)
теңдігі орындалсын. Жоғарыда дәлелденген тұжырымнан
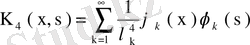 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz