Массалар центрі аз ауытқыған магниттелген симметриялық жасанды жерсеріктердің прецессиясыз, нутациясыз және меншікті айналусыз қозғалысының теңдеулері, дербес шешімдері және басқару моменттері


Кіріспе
Дипломдық жұмыс кіріспеден, үш бөлімнен, қорытындыдан және қосымшадан тұрады. Бірінші бөлімде Эйлердің канондық айнымалылары арқылы массалар центрі аз ауытқыған навигациялық серіктің прецессиясыз және нутациясыз қозғалыстарының теңдеулері қорытылып, дербес шешімдері мен басқару моменттері анықталып шығарылады. Екінші бөлімде Эйлердің айнымалылары арқылы массалар центрі аз ауытқыған серіктің прецессиясыз, нутациясыз және меншікті айналусыз қозғалыстарының теңдеулері қорытылып, дербес шешімдері мен басқару моменттері анықталып шығарылады. Үшінші бөлімде анықталған дербес шешімдерінің графиктері тұрғызылып, басқару моменттерінің өзгеру заңдылығы тұрғызылады. Жер серігінің магниттік моментін дәл анықтау теориялық және тәжірибелік көзқарас тұрғысынан қарағанда өте қиын есеп болып келеді. Магниттік моменттің жеке құраушыларын жеткілікті дәлдікпен сыртқы магнит өрісінен және серіктің орналасуынан тәуелсіз деп есептеуге болады. Мұндай магниттік моменттер: тұрақты магниттермен және электрлік жүйелермен құрылатын моменттер. Магниттік моменттің басқа құраушылары жеткілікті түрде сыртқы орта мен серіктің орналасуына тәуелді болады. Барлық шығындар, сонымен қатар, капиталдық салымдар мен интеграциялау жүйесін құру мен еңгізудің экономикалық тиімділігі есептеледі. Бесінші бөлімде өмір тіршілік жағдайы қаралады. Жер серігіне әсер ететін гравитациялық, магниттік және аэродинамикалық табиғаттың моменттері мәндері бойынша салыстырылады. Бірақ, арнайы қондырғыларды қолдану көрсетілген моменттердің біреуін басқалардан бірнеше дәрежеге артық етіп көрсетеді. Осы жағдайды ескере отырып, болашақта серік динамикасына осы моменттердің тек біреуінің әсерін қарастырамыз. Бұл басқа моменттер негізгісінен өлшемі бойынша біршама кіші және ұйытқушылар қатарына жатқызылады деген болжамға эквивалент. Мысалы, егер жер серігіне күшті магниттер орнатылған болса, онда серіктің айналмалы қозғалысы негізінен оның магниттік өрісі мен жердің магниттік өрісінің арақатынасымен анықталады. Сондықтан, магниттік моментті артық деп санап, басқа моменттердің әсерін ескермейміз. Симметриялы дененің магнит моменті симметрия өсімен бағытталған. Әртүрлі себептермен массалар центрі аз ауытқуы мүмкін. Жер серігінің массалар центрі аз ауытқығандағы және серік қабыршағының магниттелуін ескеріп серіктің қозғалысын қарастыралық.
Монитордан шығатын зиянды электрмагниттiк толқындардың әсері, жұмыс аймағының жеткiлiксiз жарықтығы, сыртқы ортаның үлкен температурасы, табиғи жарықтың жоқтығы немесе кемшiлiгi деген сұрақтар қарастырылады. Серіктерді навигациялық есептерді шешуге қолданудың маңыздылығы негізінен оның Жердің үлкен аймағынан немесе Жер маңындағы кеңістіктен көріну мүмкіндіктеріне байланысты. Бұл жағдай, навигациялық ақпаратты қолданушы болатын, объектінің көріну аймағын серіктің көру аймағына дейінгі мәнге біршама үлкейтуге, сондай-ақ объектінің, анықталатын объектіден үлкен қашықтықта орналасқан, координатасы белгілі объектіге қатысты навигациялық анықтама жүргізуге мүмкіндік береді. Ол үшін анықталатын объект серіктің көру аймағында орналасуы қажет.
Дипломдық жұмыста массалар центрі аз ауытқуындағы магниттелетін навигациялық және массалар центрі аз ауытқуындағы магниттелетін серіктердің сәйкес прецессиясыз, нутациясыз және меншікті айналусыз қозғалыстарының дербес шешімдері мен басқару моменттері қорытылып, арасындағы тәуелділік заңдылығы құрылады.
Бұл жұмыста қабыршағы магниттелген симметриялы серіктің массалар центрі аз ауытқығандағы ұйытқымалы қозғалысының дербес шешімдері мен олардың арасындағы байланысы қарастырылады. Қозғалыстағы серіктің кинетикалық энергиясын азайту үшін магниттік демферлер құрумен активті және пассивті магниттік тұрақтандыру теориясында аз ауытқуы бар стационар қозғалыстарды зерттеу маңызды болып табылады.
Сонымен қатар, магниттелген динамикалық симметриялы жасанды жер серіктің, оның қабыршағының магниттелуінің және массалар центрі аз ауытқуының салдарынан пайда болған ұйытқуды ескеріп, сондай-ақ ұйытқусыз, қабыршағы магниттелетін және серіктің массалар центрі аз ауытқитын әртүрлі жағдайлардағы навигациялық серіктердің қозғалыстарын қарастырылады. Тәуелділік графиктерін MatLab бағдарламалау ортасы көмегімен тұрғызылады.
1 Массалар центрі аз ауытқыған магниттелген серіктің қозғалысы
1. 1 Жердің магнит өрісінде қозғалатын серікке әсер ететін күштер туралы мәліметтер
Магниттелген дененің кернеулігін Н магниттік өріске орналастыратынболсақ, онда бұл денеге келесі формуламен анықталатын күш моменті әсеретеді.
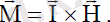 (1. 1)
(1. 1)
Мұндағы:Н - дененің магниттік моменті. I -дененің магниттік моменті.
Жер серігіндегі магниттік момент онда функционалдаушы электрлік жүйелердің және тұрақты магниттердің бар болуынан, сондай-ақ серіктің металды корпусының магниттелуінен пайда болады.
Жер серігінің магниттік моментін дәл анықтау теориялық және тәжірибелік көзқарас тұрғысынан қарағанда өте қиын есеп болып келеді. Магниттік моменттің жеке құраушыларын жеткілікті дәлдікпен сыртқы магнит өрісінен және серіктің орналасуынан тәуелсіз деп есептеуге болады. Мұндай магниттік моменттер: тұрақты магниттермен және электрлік жүйелермен құрылатын моменттер. Магниттік моменттің басқа құраушылары жеткілікті түрде сыртқы орта мен серіктің орналасуына тәуелді болады. Олар, келтірілген (наведенный) магниттік момент және Фуко токтарының әсерінен пайда болатын магниттік момент болып табылады. Кеңістіктің жер серігі орналасқан бөлігінде сыртқы геомагниттік өріс біртектіге жақын болғандықтан, магниттік моментті есептеу біршама жеңілдетіледі.
Жер серігінің магниттік моменті I0 тұрақты құраушы мен IH қабыршақтың магниттік моментінің қосындысынан тұрады деп есептейік, яғни
 (1. 2)
(1. 2)
Мұнда құйынды токтардың магниттік моменттерінің әсерін ескермейміз.
Тұрақты магниттік моментінің жер серігі денесіндегі орнын бағыттаушыкосинустар кестесімен анықталық.
 (1. 3)
(1. 3)
Анықтау үшін, Oz өсінің бағытын
 моментінің осы өске проекциясы теріс болатындай етіп таңдап алынған деп санаймыз.
моментінің осы өске проекциясы теріс болатындай етіп таңдап алынған деп санаймыз.
Жеткілікті созылған симметриялы дене магниттелген өрісте негізінен өзінің симметрия өсінің бойында магниттелетіні белгілі және келтірілген магниттік момент сыртқы өрістің кернеулік векторының дененің симметрия өсіне проекциясына пропорционал болады. Серік қабыршағының симметрия өсі оның бас инерция өстерінің бірімен, мысалы,
z
өсімен сәйкес келеді деп есептелік. Онда қабыршақтың
 магниттік моментін келесі формуламен анықтауға болады:
магниттік моментін келесі формуламен анықтауға болады:

мұндағы, z 0 - z осінің ортасы, β3 - z 10 векторының бағыттаушы косинусы, ς - серік қабыршағының магниттелуін сипаттайтын параметр және де бұл келесідей анықталады:

мұндағы: µ0 - серік қабыршағының материалының салыстырмалы магниттік өтімділігі, µ1 - Жердің магниттелуінің тұрақтысы; ν - көлем; R - жер серігінің массалар центірінің радиус-векторы.
Өткізгіште Фуко токтары (құйынды токтар) - магниттік өрістің күш сызығымен қиылысқан кезде пайда болады, бірақ та біз оларды ескермейміз.
Жер серігінде үлкен магниттік момент құру қажет болған жағдайда, не серікте орнатылған, орамдарының бойымен ток өтетін, соленоидтар, не тұрақты стержендік магниттер қолданылады. Соленоидтар негізінен серіктің активті басқару жүйесінде, ал тұрақты магниттер геомагниттік өріс бойында пассивті стабилизация жүйелерінде қолданылады.
Жер серігіне магниттік күш моменттерінен басқада көптеген моменттер әсер етеді. Онша үлкен емес орбита үшін ең алдымен гравитациялық және аэродинамикалық моменттерді ескеру қажет.
Жер серігінің атмосферамен әсерлесуі, серікті қума ағыстың (набегающий поток) бағытына сәйкес орналастыруға тырысатын, моменттің пайда болуына және оның айналуының тежелуіне әкеліп соғады.
Жер серігіне әсер ететін гравитациялық, магниттік және аэродинамикалық табиғаттың моменттері мәндері бойынша салыстырылады. Бірақ, арнайы қондырғыларды қолдану көрсетілген моменттердің біреуін басқалардан бірнеше дәрежеге артық етіп көрсетеді. Осы жағдайды ескере отырып, болашақта серік динамикасына осы моменттердің тек біреуінің әсерін қарастырамыз. Бұл басқа моменттер негізгісінен өлшемі бойынша біршама кіші және ұйытқушылар қатарына жатқызылады деген болжамға эквивалент. Мысалы, егер жер серігіне күшті магниттер орнатылған болса, онда серіктің айналмалы қозғалысы негізінен оның магниттік өрісі мен жердің магниттік өрісінің арақатынасымен анықталады. Сондықтан, магниттік моментті артық деп санап, басқа моменттердің әсерін ескермейміз.
Симметриялы дененің магнит моменті симметрия өсімен бағытталған. Әртүрлі себептермен массалар центрі аз ауытқуы мүмкін. Жер серігінің массалар центрі аз ауытқығандағы және серік қабыршағының магниттелуін ескеріп серіктің қозғалысын қарастыралық.
1. 2 Массалар центрі аз ауытқыған серіктің қозғалысы туралы мәселенің қойылуы
Магниттелген динамикалық симметриялы серіктің, оның қабыршағының магниттелуінің және массалар центрінің аз ауытқуының салдарынан пайда болған, ұйытқуды ескеріп, сондай-ақ ұйытқусыз, қабыршағы магниттелетін және серіктің массалар центрі аз ауытқитын әр-түрлі жағдайлардағы навигациялық және навигациялық емес серіктердің қозғалыстарын қарастырайық. Серіктің массалар центрі экваториалды жазықтықта дөңгелек орбитамен қозғалады. Серікке күшті магниттер орнатылған, сондықтан оның массалар центрінің айналасындағы қозғалысы, негізінен, оның магниттік моменті мен тура дипольмен моделденетін Жердің магнит өрісінің өзара әсерлесуімен анықталады [1], [2] . Геомагниттік өріс тура дипольмен моделденеді.
Жер серігінің қозғалысын сипаттау үшін орбитал координаталар жүйесі мен серікке қатаң бекітілген координаталар жүйесінің өстерінің арасындағы бұрыштарды енгізу ыңғайлы . Яғни, басы жер серігінің массалар центрінде болатын Oxyz координаталар жүйесі, z өсі массалар центрінің орбитасының радиус-векторының бойымен бағытталған, х өсі - орбитаға транверсал бойымен және у өсі - орбитаның жазықтығына нормаль бойымен бағытталған. Ox 1 у 1 z 1 жүйесі серікке қатаң бекітілген; z 1 өсі серіктің динамикалық симметрия өсімен сәйкес келеді.
Серікке қатаң бекітілген координаталар жүйесінің орбиталды координаталар жүйесіне қатысты орны φ, ψ, θ (φ- меншікті айналыс бұрышы, ψ - прецессия бұрышы, θ - нутация бұрышы) Эйлер бұрыштарымен анықталады. Эйлер бұрыштары төменгі суретте көрсетілгендей берілген. Серіктің қозғалысын негізгі Оξηζ координаталар жүйесіне байланыстырамыз.
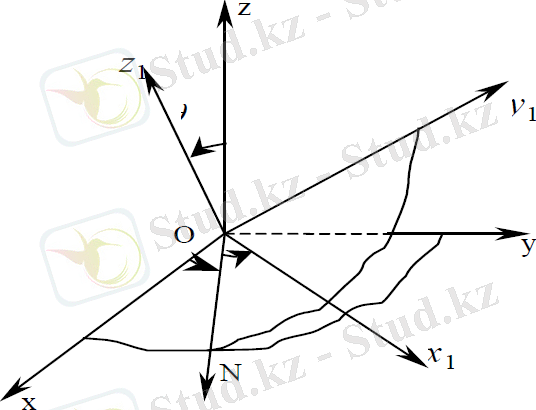
сурет 1. 1 Координаталар жүйелері
Қарастырылып отырған жағдайда жердің жасанды серігінің массалар центрі экваториалды жазықтықта дөңгелек орбитамен қозғалсын, онда геомагниттік өрістің кернеулігі абсолют кеңістікте қозғалмайды, әрі серіктің орбитасының жазықтығына нормаль бойымен бағытталады және тұрақты мәнге ие болады:
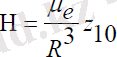 (1. 4)
(1. 4)
мұндағы, z10 - z1 өсінің ортасы, µe - Жердің магниттелуінің тұрақтысы, R - Жерге қатысты серіктің массалар центрінің радиус-векторы [2] .
Абсолют бұрыштық жылдамдықтың бас инерция өстеріне проекциясы былай жазылады:
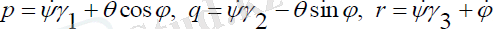 (1. 5)
(1. 5)
Мұндағы, φ’, ψ’, θ’ - сәйкесінше меншікті айналыс, прецессия, нутация бұрыштарының бұрыштық жылдамдықтары, ал γ1, γ2, γ3 - бағыттаушы косинустардың мәндері, олар орбиталды координаталар жүйесінің айналуының бұрыштық жылдамдықтарын береді және былай анықталады:
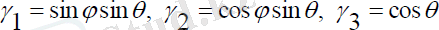 .
.
1. 3 Серіктің кинетикалық энергиясы мен ұйытқу функциясы
:

Бірақ, , яғни A=B болғандықтан, :
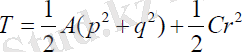 (1. 6)
(1. 6)
мұндағы, А=B, C - серіктің бас инерция моменттері.
Болашақта әртүрлі жағдайда Жердің жасанды серігінің қозғалыс теңдеуін құру кезінде қажет болатын өрнектерді құрайық:
 (1. 7)
(1. 7)
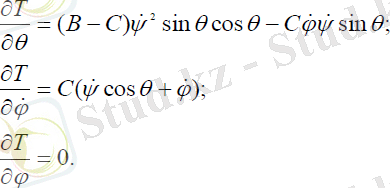
Серіктің массалар центрі аз ауытқуының серік қабыршағының магниттелуінің салдарынан туындаған аз ұйытқуды сипаттайтын функцияны келесі түрде жазалық:
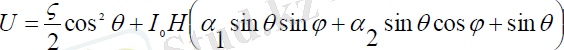 (1. 8)
(1. 8)
Онда:
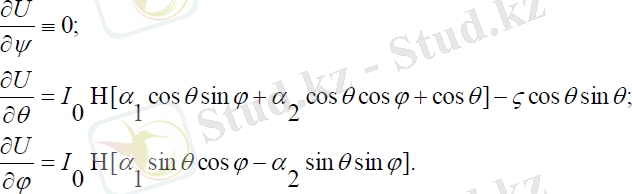 (1. 9)
(1. 9)
. Сондықтан, : .
1. 4 Навигациялық серік туралы мәлімет
. Бұлжағдай, , , сондай-ақобъектінің, , . Ол үшін анықталатын объект серіктің көру аймағында орналасуы қажет.
Навигациялық серіктер биіктігі 600 . . . 36000 км болатын орбитаға шығарылады. Төменгі биіктіктегі навигациялық серіктердің орбитасының биіктігі 600 . . . 3000 км және айналу периоды 0, 5 . . . 2, 5 сағат. Орташа биіктіктегі навигациялық серіктер 13000 . . . 2 км биіктіктегі диапазонда орналасқан, ал айналу периоды 8 сағаттан 12 сағатқа дейін созылады. Ең үлкен биіктіктегі орбиталар (36100 км) геосинхронды серіктерге тән болады, олардың айналу периоды Жердің өзінің айналу осіне қатысты толық бұрылуына тең болады, яғни 24 сағат. Мұндай серіктер, олардың орбитамен айналу бұрыштық жылдамдықтарының Жердің айналу бұрыштық жылдамдығына тең болуына байланысты, белгілі бір нүктенің үстінде тұрып қалады. Мұндай навигациялық серіктер көру аймағы неғұрлым үлкен, бұрыштық диаметрі 162о болғандықтан, теориялық және практикалық көзқарас тұрғысынан қарағанда навигациялық есептерді шешуде эффективті болып келеді.
Сурет 1. 2 Жер серіктің дөңгелек орбитадағы тепе-теңдік жағдайлары
2 Массалар центрі аз ауытқыған навигациялық магниттелган серіктің қозғалыс теңдеулері мен дербес шешімдері
2. 1 Ұйытқушы күштері жоқ навигациялық серіктің нутациясыз және прецессиясыз қозғалыс теңдеулерімен дербес шешімдері
Навигациялық серіктер үшін меншікті айналу бұрыштық жылдамдық тұрақты болады, яғни . φ=const.
Прецессиясыз қозғалысты қарастырайық, яғни ψ=ψ0; ψ=0 .
Қозғалыс теңдеуін құрайық:
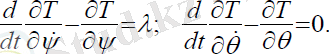 (2. 1)
(2. 1)
Сонда (1. 7) өрнектерді ескеріп, ізделініп отырған, шамаларына байланысты екі сызықсыз екінші ретті теңдеулер жүйесін аламыз:
 (2. 2)
(2. 2)
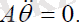
(2. 2) :
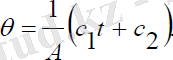 (2. 3)
(2. 3)
Мұндағы, c1, c2 - интегралдау тұрақтылары.
Яғни, меншікті айналу және прецессия бұрыштары тұрақты шамаларға тең, ал нутация бұрышы сызықты заңмен өзгергенде басқару моменті қажет болмайды.
Нутациясыз қозғалыс
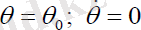 шарттарымен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
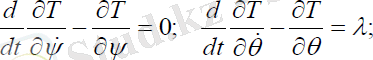 (2. 4)
(2. 4)
Оларізделінді
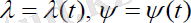 :
:
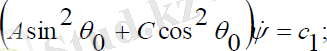 (2. 5)
(2. 5)
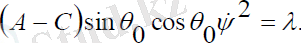
Мұндағы, c1= const. (2. 4) , :
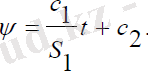 (2. 6)
(2. 6)
Мұндағы:
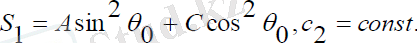
:
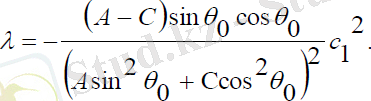 (2. 7)
(2. 7)
, алпрецессиябұрышы (2. 6) (2. 7) қатынасыменанықталады.
2. 2 Магниттелетін навигациялық серіктің прецессиясыз және нутациясыз қозғалыстеңдеулерімен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
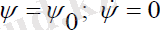 шарттары орындалатын жағдайдағы қозғалыс.
шарттары орындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құралық:
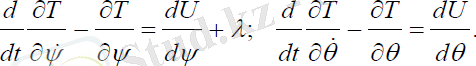 (2. 8)
(2. 8)
Сонда (1. 7) өрнектерді ескеріп, ізделініп отырған шамаларына байланысты екісызықсыз екінші ретті теңдеулер жүйесін аламыз:
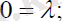 (2. 9)
(2. 9)
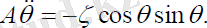
(2. 9) жүйенің екінші теңдеуі сызықты емес екінші ретті дифференциалдық теңдеу. θ - ға қатысты бір рет интегралдасақ, бірінші ретті сызықты емес дифференциалдық теңдеу аламыз:
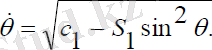 (2. 10)
(2. 10)
Мұндағы,
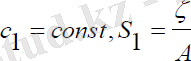 .
.
(2. 10) -дың шешімін бастапқы шарттар бере отырып Рунге-Куттыңсандық әдісі көмегімен есептейміз. Есептеу жолы жұмыстың .
Нутациясыз қозғалыс
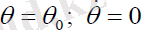 шарттарымен анықталады. Онданавигациялық серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онданавигациялық серіктің қозғалыс теңдеуі мына түрде болады:
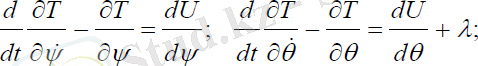 (2. 11)
(2. 11)
Олар ізделінді
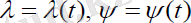 шамаларына қатысты екі теңдеулер жүйесін береді:
шамаларына қатысты екі теңдеулер жүйесін береді:
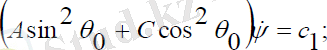 (2. 12)
(2. 12)
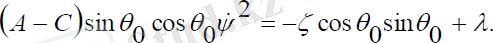
Мұндағы, c1=const .
(2. 12) теңдеулер жүйесінің бірінші теңдеуінен прецессия бұрышыныңжылдамдығы тұрақты, оны интегралдасақ прецессия бұрышы мынадайсызықты заңмен өзгеретінін көреміз:
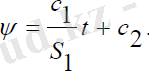 (2. 13)
(2. 13)
Мұндағы:
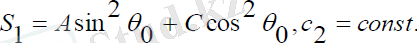
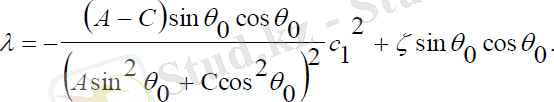 (2. 14)
(2. 14)
Прецессиясыз қозғалысты қамтамасыз ететін басқару функциясы: (2. 14)
Меншікті айналу және нутация бұрыштары тұрақты шамаларға тең, ал прецессия бұрышы (2. 13) сызықты заңмен өзгергенде басқару моменті (2. 14) қатынасымен анықталады.
2. 3 Массалар центрі аз ауытқыған навигациялық серіктің прецессиясыз және нутациясыз қозғалыс теңдеулері мен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
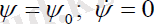 шарттары орындалатын жағдайдағы қозғалыс.
шарттары орындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құрайық:
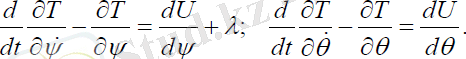 (2. 15)
(2. 15)
Сонда (1. 7) өрнектерді ескеріп, ізделініп отырған
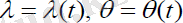 шамаларына байланысты екі сызықсыз екінші ретті теңдеулер жүйесін аламыз:
шамаларына байланысты екі сызықсыз екінші ретті теңдеулер жүйесін аламыз:

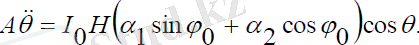 (2. 16)
(2. 16)
(2. 16) жүйенің екінші теңдеуін қатысты бір рет интегралдасақ:
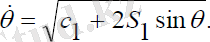 (2. 17)
(2. 17)
Мұндағы:
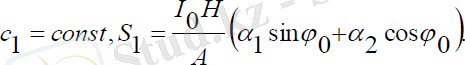
(2. 17) теңдеуінің шешімін бастапқы шарттар бере отырып Рунге-Куттың сандық әдісі көмегімен есептелінеді. Есептеуі қосымшада келтіріледі. Бұл жағдайда да басқару моменті нөлге тең, демек, массалар центрі аз ауытқыған навигациялық серіктің прецессиясыз қозғалысы кезінде басқару моменті қажет болмайды.
Нутациясыз қозғалыс
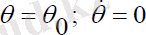 шарттарымен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
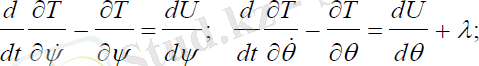 (2. 18)
(2. 18)
Олар ізделінді
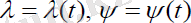 шамаларына қатысты екі теңдеулер жүйесін береді:
шамаларына қатысты екі теңдеулер жүйесін береді:
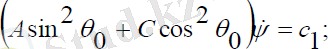 (2. 19)
(2. 19)
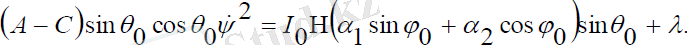
Мұндағы, c 1 =cons (2. 19) теңдеулер жүйесінің бірінші теңдеуінен прецессия бұрышының жылдамдығы тұрақты, яғни прецессия бұрышы мынадай сызықты заңымен өзгереді:
 (2. 20)
(2. 20)
Мұндағы:
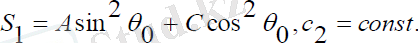
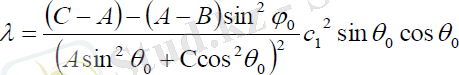 (2. 21)
(2. 21)
Меншікті айналу және нутация бұрыштары тұрақты шамаларға тең, ал прецессия бұрышы (2. 20) сызықты заңмен өзгергенде басқару моменті (2. 21) қатынасы мен анықталады.
2. 4 Массалар центрі аз ауытқыған магниттелетін навигациялық серіктің прецессиясыз және нутациясыз қозғалыс теңдеулері мен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
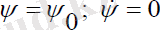 шарттары орындалатын жағдайдағы қозғалыс.
шарттары орындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құрайық:
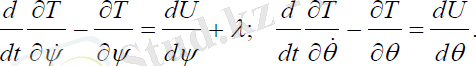 (2. 22)
(2. 22)
Сонда (1. 7) өрнектердіескеріп, ізделініпотырғанλ =λ( t ), θ =θ ( t ) :
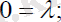
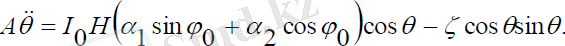 (2. 23)
(2. 23)
(2. 22) :
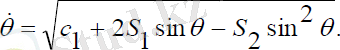 (2. 24)
(2. 24)
:
Мұндағы:
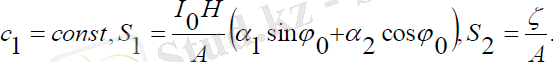
(2. 24) теңдеуінің шешімін бастапқы шарттар берео тырып, Рунге-Куттың санды қәдісі көмегімен есептелінеді. Есептеуі қосымшада келтіріледі. Бұл жағдайда да басқару моменті нөлге тең, демек, массалар центрі аз ауытқыған магниттелетін навигациялық серіктің прецессиясыз қозғалысы кезінде басқару моменті қажет болмайды.
Нутациясыз қозғалыс
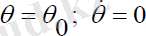 шарттары мен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
шарттары мен анықталады. Онда навигациялық серіктің қозғалыс теңдеуі мына түрде болады:
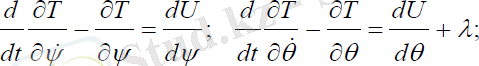 (2. 25)
(2. 25)
Олар ізделінді
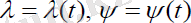 шамаларына қатысты екі теңдеулер жүйесін береді:
шамаларына қатысты екі теңдеулер жүйесін береді:
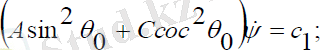 (2. 26)
(2. 26)
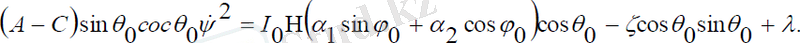
Мұндағы, c 1 =const . (2. 26) теңдеулер жүйесінің бірінші теңдеуінен прецессия бұрышының жылдамдығы тұрақты, яғни прецессия бұрышы мынадай сызықты заңымен өзгереді:
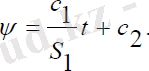 (2. 27)
(2. 27)
Мұндағы:
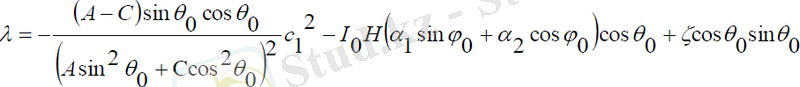 (2. 28)
(2. 28)
Меншікті айналу және нутация бұрыштары тұрақты шамаларға тең, ал прецессия бұрышы (2. 27) сызықты заң мен өзгергенде басқару моменті (2. 28) қатынасымен анықталады. Онда серік нутациясыз регулярлы прецессия жасайтыны көрсетіледі.
3 Массалар центрі аз ауытқыған магниттелген серіктің қозғалыс теңдеулері мен дербес шешімдері
3. 1 Ұйытқушы күштері жоқ серіктің прецессиясыз, нутациясыз және меншікті айналусыз қозғалыс теңдеулері мен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
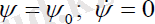 шарттары орындалатын жағдайдағы қозғалыс.
шарттары орындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құрайық:
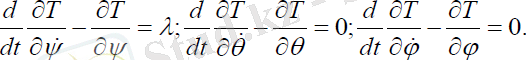 (3. 1)
(3. 1)
Сонда (1. 7) өрнектердіескеріп, ізделініпотырған
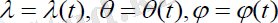 :
:
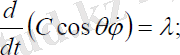
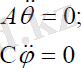 (3. 2)
(3. 2)
(3. 2) , θжәне :
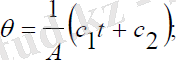 (3. 3)
(3. 3)

Мұндағы, c1, c2, c3, c4 - интегралдау тұрақтылары.
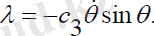 (3. 4)
(3. 4)
Демек, , .
Нутациясыз қозғалыс
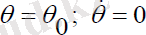 шарттары мен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
шарттары мен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
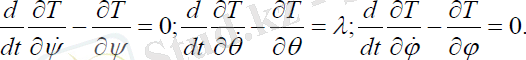 (3. 5)
(3. 5)
Олар ізделінді
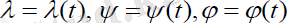 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
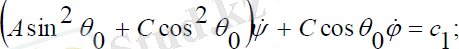
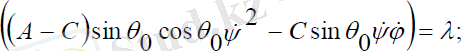 (3. 6)
(3. 6)
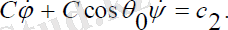
Мұндағы, c1, c2 - интегралдау тұрақтылары. (3. 6) теңдеулер жүйесінің бірінші және үшінші теңдеулерін бір-біріне қатысты өрнектеп, шешетін болсақ, онда прецессиямен меншікті айналу бұрыштарын анықтайтын мынадай тәуелділіктерді аламыз:
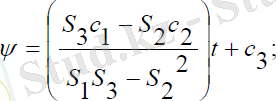 (3. 7)
(3. 7)
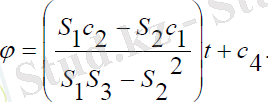
Мұндағы:
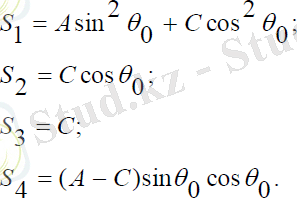
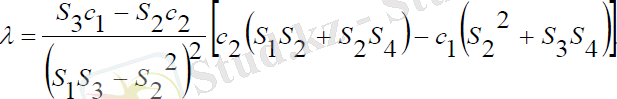 (3. 8)
(3. 8)
Нутация бұрышы тұрақты болғанда прецессия және меншікті айналу бұрыштары (3. 7) сызықты қатынастарымен анықталып, басқару моменті (3. 8) шамасына тең болады.
Меншікті айналусыз қозғалыс
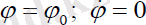 шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
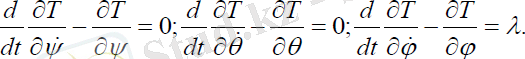
Олар ізделінді
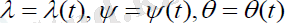 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
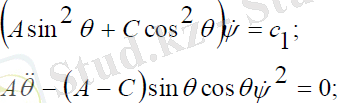 (3. 10)
(3. 10)
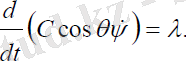
Мұндағы, c1- интегралдау тұрақтысы. (3. 10) теңдеулер жүйесінің біріншісінен ψ - прецессия бұрышының жылдамдығын тауып, екінші теңдеуге қойып, θ -ға бір рет интегралдасақ, θ -ға және ψ -ге қатысты бірінші ретті сызықты емес теңдеулер жүйесін аламыз:
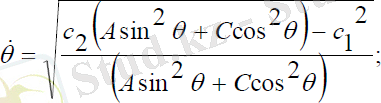 (3. 11)
(3. 11)
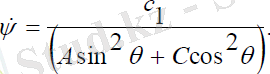
Мұндағы, c2- интегралдау тұрақтысы.
Ал басқару моменті нутация бұрышына тәуелді өзгеріп, келесі қатынаспен анықталады:
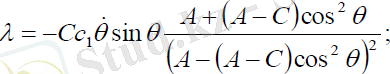 (3. 12)
(3. 12)
(3. 11) теңдеулер жүйесінің шешімін Рунге-Куттың сандық әдісі көмегіменқосымшада келтірілген.
3. 2 Магниттелетін серіктің прецессиясыз, нутациясыз және меншікті айналусыз қозғалыс теңдеулері мен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
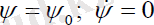 ; шарттарыорындалатын жағдайдағы қозғалыс.
; шарттарыорындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құрайық:
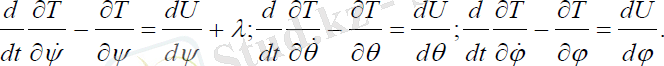 (3. 13)
(3. 13)
Сонда (1. 7) өрнектерді ескеріп, ізделініп отырған λ =λ( t ), θ =θ ( t ), ϕ =ϕ( t ) шамаларына байланысты үш екінш іретті теңдеулер жүйесін аламыз:
 (3. 14)
(3. 14)
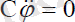
(3. 14) :
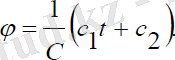 (3. 15)
(3. 15)
Мұндағы:c1, c2- интегралдау тұрақтылары. (3. 14) жүйенің екіншітеңдеуін θ -ға қатысты бір рет интегралдасақ, онда бірінші ретті сызықты еместеңдеу аламыз:
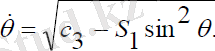 (3. 16)
(3. 16)
Мұндағы,
c3=const
,
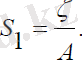
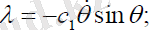 (3. 17)
(3. 17)
(3. 16) теңдеудің шешімі Рунге-Куттың санды қәдісі көмегімен қосымшада келтірілген.
Нутациясыз қозғалыс
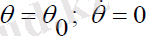 шарттарымен анықталады. :
шарттарымен анықталады. :
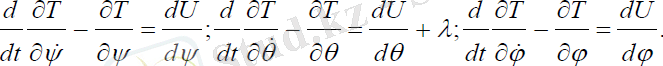 (3. 18)
(3. 18)
Олар ізделінді
 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
 (3. 19)
(3. 19)
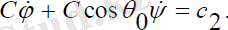
Мұндағы, c1, c2- интегралдау тұрақтылары
(3. 19) теңдеулер жүйесінің біріншімен үшінші теңдеуілерінб ір-біріне қатысты өрнектеп шешетін болсақ, онда мынадай тәуелділікті аламыз:
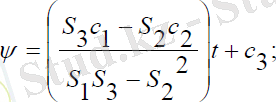 (3. 20)
(3. 20)
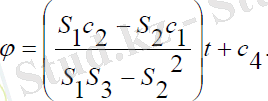
Мұндағы:

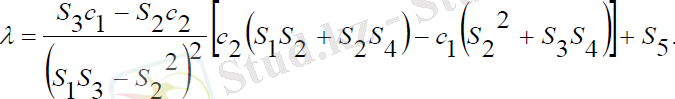 (3. 21)
(3. 21)
Нутация бұрышы тұрақты болғанда, прецессия және меншікті айналу бұрыштары (3. 20) сызықты қатынастары мен анықталып, басқару моменті (3. 21) шамасына тең болады.
Меншікті айналусыз қозғалыс
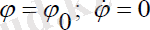 шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
 (3. 22)
(3. 22)
Олар ізделінді
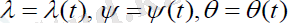 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
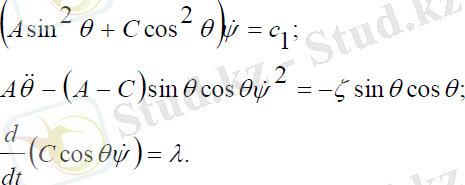 (3. 23)
(3. 23)
Мұндағы, с1 - интегралдау тұрақтысы.
(3. 23) теңдеулер жүйесінің бірінші теңдеуінен ψ -прецессия бұрышының жылдамдығын тауып, екінші теңдеуге қойып, θ -ға бір рет интегралдасақ, θ - ға және ψ -ге қатысты бірінші ретті сызықты емес теңдеулер жүйесін аламыз:
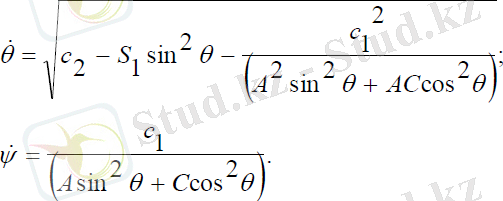 (3. 24)
(3. 24)
Мұндағы,
c2=const
,
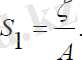
Ал басқару моменті (3. 23) жүйенің үшінші теңдеуін шешу арқылы, былай анықталады:
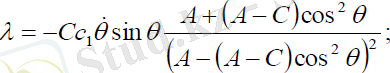 (3. 25)
(3. 25)
(3. 24) теңдеулер жүйесінің шешімін Рунге-Куттың сандық әдісікөмегімен қосымшада келтірілген.
3. 3 Массалар центрі аз ауытқыған серіктің прецессиясыз, нутациясыз және меншікті айналусыз қозғалыс теңдеулері мен дербесшешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
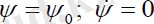 шарттарыорындалатын жағдайдағы қозғалыс.
шарттарыорындалатын жағдайдағы қозғалыс.
Қозғалыс теңдеуін құрайық:
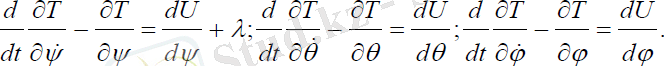 (3. 26)
(3. 26)
Сонда (1. 7) өрнектерді ескеріп, ізделініп отырған
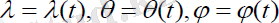 шамаларына байланысты үш екінші ретті теңдеулер жүйесін аламыз:
шамаларына байланысты үш екінші ретті теңдеулер жүйесін аламыз:
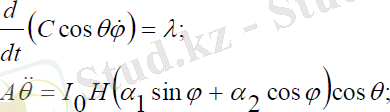 (3. 27)
(3. 27)
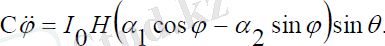
(3. 27) жүйенің соңғы екі теңдеуі екінші ретті сызықсыз теңдеулер. Осы теңдеулер шешімдері Рунге-Куттың сандық әдісімен қосымшада келтірілген.
Нутациясыз қозғалыс
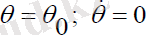 шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
шарттарымен анықталады. Онда серіктің қозғалыс теңдеуі мына түрде болады:
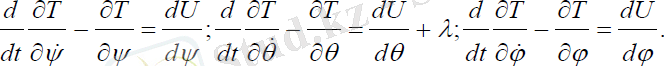 (3. 28)
(3. 28)
Олар ізделінді
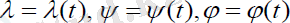 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
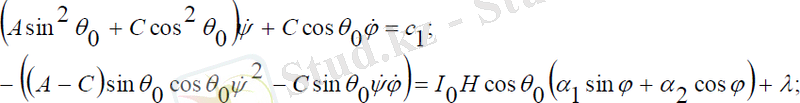
 (3. 29)
(3. 29)
Мұндағы, с1 - интегралдау тұрақтысы. (3. 29) теңдеулер жүйесінің біріншісінен ψ-ды өрнектеп, осы жүйенің үшінші теңдеуіне қойып, ψ - ға бір рет интегралдасақ, онда ψ - ге қатысты бірінші ретті сызықсыз теңдеу аламыз.
Оған қоса жүйенің бірінші теңдеуін ескерсек, келесідей бірінші ретті теңдеулержүйесін аламыз:
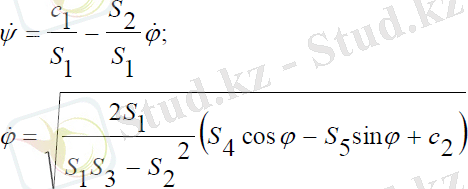 (3. 30)
(3. 30)
Мұндағы:
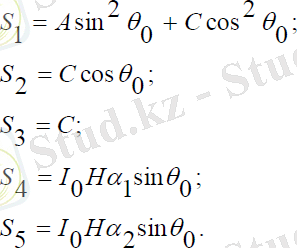
Мұндағы, с2- интегралдау тұрақтысы. (3. 30) теңдеулер жүйесі біріншіретті сызықсыз болғандықтан, Рунге-Куттың сандық әдісі көмегімен шешілгеншешімі қосымшада келтірілген.
Меншікті айналусыз қозғалыс
 шарттарымен анықталады.
шарттарымен анықталады.
Онда серіктің қозғалыс теңдеуі мына түрде болады:
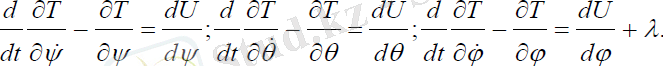 (3. 31)
(3. 31)
Олар ізделінді
 шамаларына қатысты үш теңдеулер жүйесін береді:
шамаларына қатысты үш теңдеулер жүйесін береді:
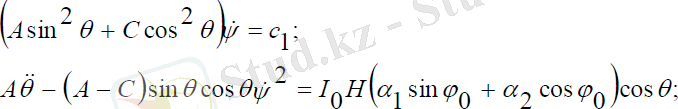 (3. 32)
(3. 32)
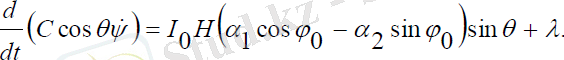
Мұндағы, с1- интегралдау тұрақтысы. (3. 32) теңдеулер жүйесініңбіріншісінен ψ-прецессия бұрышының жылдамдығын тауып екінші теңдеугеқойып, θ -ға бір рет интегралдасақ, θ - ға және ψ -ге қатысты бірінші реттісызықты емес теңдеулер жүйесін аламыз:
 (3. 33)
(3. 33)

Мұндағы:
c2=const
,
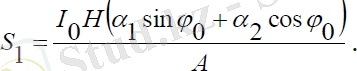
(3. 33) теңдеулер жүйесінің шешімі Рунге-Куттың сандық әдісі көмегіменқосымшада келтірілген.
3. 4 Массалар центрі аз ауытқыған магниттелетін серіктіңпрецессиясыз, нутациясыз және меншікті айналусыз қозғалыс теңдеулерімен дербес шешімдері
Прецессиясыз қозғалысты қарастырайық, яғни
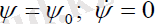 шарттарыорындалатын жағдайдағы қозғалыс.
шарттарыорындалатын жағдайдағы қозғалыс.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz