Дискреттеу және сигналдарды қалпына келтіру: кванттау, Котельников теоремасы және дискретті Лаплас, Фурье, Z түрленістері


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:
1 Дискреттеу және дабылдарды қалпына келтіру
1. 1 Дабылдарды Дискреттеу
Деңгей бойынша Дискреттеу (кванттау) деп кванттау шкаласының шешілген мәніне шаманың үздіксіз мәнің жатқызатын операцияны түсінеді. Математикалық көзқарастан кванттау операциясына сәйкес келетін шешу тәртібімен (кванттаудың төменгі шекарасынан жоғарғы шекарасына немесе оның ортасына) үздіксіз шаманың мәнің анықтауға байланысты. Сандық бағаны алу үшін деңгей бойынша кванттаудан кейін кодтау операциясына көшеміз.
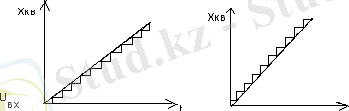
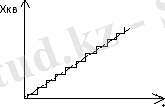
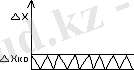
1. 1 - сурет
Суретте бірқалыпты деңгей бойынша кванттау операциясы көрсетілген, үздіксіз шаманың мәнінің мүмкін диапазоны Х кванттаудың тең интервалдарына n бөлінеді.
Кванттаудың әрбір интервалының ұзындығы кванттау қадамы деп аталады.
Бірінші және екінші жағдайда да абсолютті қателік кванттау қадамына тең, соңғысында - кванттау қадамының жартысына .
Сандық өлшеу аспаптарында кванттау автоматты түрде орындалады. Деңгей бойынша кванттау, экспериментатордың аналоготы аспабының шкаласынан саналатың, сандық регистрация бойынша орындалады.
1. 2 Уақыт бойынша Дискреттеу
Уақыт бойынша үздіксіз функциядан дискретті уақыт функциясына өтудің ең қарапайым тәсілі, белгілі дискретті уақыт кезінде функция санауынан алу жолмен орындалады. Нәтижесінде
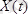 үздіксіз функциясы
үздіксіз функциясы
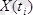 әп-сәттегі мәндердің жиынтығымен алмастырылады.
әп-сәттегі мәндердің жиынтығымен алмастырылады.
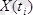 мәндері бойынша берілген дәлдікпен алдыңғысың қалпына келтіретің жаңа функцияны қалпына келтіруге болады
мәндері бойынша берілген дәлдікпен алдыңғысың қалпына келтіретің жаңа функцияны қалпына келтіруге болады
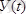 .
.
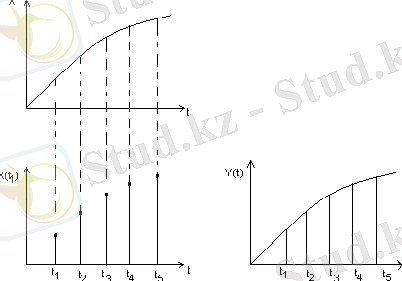
1. 2 - сурет
Интервал аз болған сайын, функцияның қалпына келуі дәлдірек болады. Котельников теоремасына сәйкес кванттаудың ең тиімді интервалы таңдалады, ол келесідей болады: егер функция
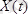 жиілігі қию жиілігінен жоғары болмаса
жиілігі қию жиілігінен жоғары болмаса
 , онда ол сол уақытта толығымен өзінің әп-сәттегі мәнімен анықталады, бір-бірінен
, онда ол сол уақытта толығымен өзінің әп-сәттегі мәнімен анықталады, бір-бірінен
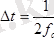 , сек шамаға қалады.
, сек шамаға қалады.
1. 3 Котельников Теоремасы
Котельников теоремасына сәйкес үздіксіз функция шексіз мүшелерінің қосындысымен Котельников қатары түрінде келтірілген.
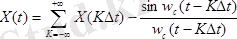 ;
;
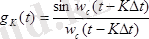 ;
;
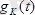 - оның қасиеттерінің функция санағы
- оның қасиеттерінің функция санағы
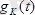
1.
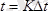 уақыты кезінде ол ең үлкен мәнге жетеді, 1 тең.
уақыты кезінде ол ең үлкен мәнге жетеді, 1 тең.
2.
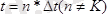 уақыты кезінде функция санағы 0 тең.
уақыты кезінде функция санағы 0 тең.
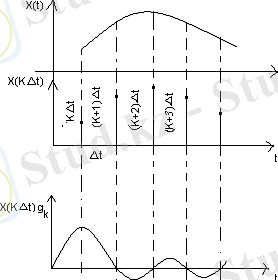
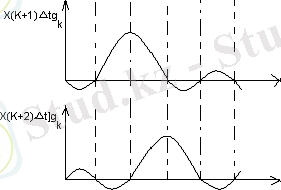
1. 3 сурет
Котельников қатарына жаюдың практикалық маңызы мұнда, ол байланыс каналдары арқылы
 торланған функцияның мәні жіберіледі және бастапқы функцияның санағы емес. Байланыс каналдары арқылы
торланған функцияның мәні жіберіледі және бастапқы функцияның санағы емес. Байланыс каналдары арқылы
 үздіксіз функцияны жіберу үшін, келесі операцияларды орындау қажет:
үздіксіз функцияны жіберу үшін, келесі операцияларды орындау қажет:
1.
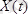 функциясының
функциясының
 уақыт кезіндегі
уақыт кезіндегі
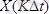 санақтарын алу керек.
санақтарын алу керек.
2. Байланыс каналдары арқылы бұл шамаларды кез келген келетін әдіспен жіберу.
3. Қабылдау бөлігіндегі жіберілген санақтарды қалпына келтіру және тең немесе пропорционалды санағы бар амплитудаларымен импульстарды құру .
4. Төмеңгі жиіліктегі идиалды функцияның кірісіне осы импульстарды беру, екіншісінің шығысында сәйкес функциялар санағы қалыптасады.
5. Алынған функцияларды қосылғаннан кейін бастапқы функцияны
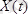 табу немесе оған ұқсасын.
табу немесе оған ұқсасын.
Шынайы жағдайларда үздіксіз шаманы тура қалпына келтіруге болмайды, себебі қию жиілігін
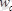 және сәйкес келетің Дискреттеу қадамын
және сәйкес келетің Дискреттеу қадамын
 таңдау, спектордың жоғары жиілікті
таңдау, спектордың жоғары жиілікті
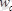 дан
дан
 дейінгі мүшелерін жоғалтуға әкеп соғады және әдістемелік қателіктің пайда болуына әкеледі.
дейінгі мүшелерін жоғалтуға әкеп соғады және әдістемелік қателіктің пайда болуына әкеледі.
2 Лапластың дискретті түрленуі
Лапластың дискретті түрленуі (ДПЛ), ДПФ сияқты, аргументті интегралді Дискреттеу түрленуі арқылы алынады (t k = kDt, w n = nDw) :
Y(p) =
 y(t) exp(-pt) dt, Y(p
n
) = Dt
y(t) exp(-pt) dt, Y(p
n
) = Dt
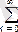 y(t
k
) exp(-p
n
t
k
), (8. 2. 1)
y(t
k
) exp(-p
n
t
k
), (8. 2. 1)
мұнда p = s+jw - комплексті жиілік, s ³ 0.
y(t) = (1/2pj)
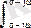 Y(p) exp(pt) dp. y(t
k
) = Dt
Y(p) exp(pt) dp. y(t
k
) = Dt
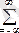 Y(p
n
) exp(p
n
t
k
) . (8. 2. 2)
Y(p
n
) exp(p
n
t
k
) . (8. 2. 2)
Y(p) функциясын Лаплас функциясының бейнесі, ал y(t) - түпнұсқа дейді. При s = 0 болса Лаплас түрленуі біржақты Фурье түрленуіне айналады, ал каузальды дабылдар үшін - ПФ толық аналогы. Лаплас түрленуі функцияның спектральді анализі үшін қолданылады, фурье бейнесі жоқ Фурье интегралынан айырмашылығы болғандықтан:
Y(p) =
 y(t) exp(-st-jwt) dt =
y(t) exp(-st-jwt) dt =
 y(t) exp(-st) exp(-jwt) dt =
y(t) exp(-st) exp(-jwt) dt =
 y'(t) exp(-jwt) dt.
y'(t) exp(-jwt) dt.
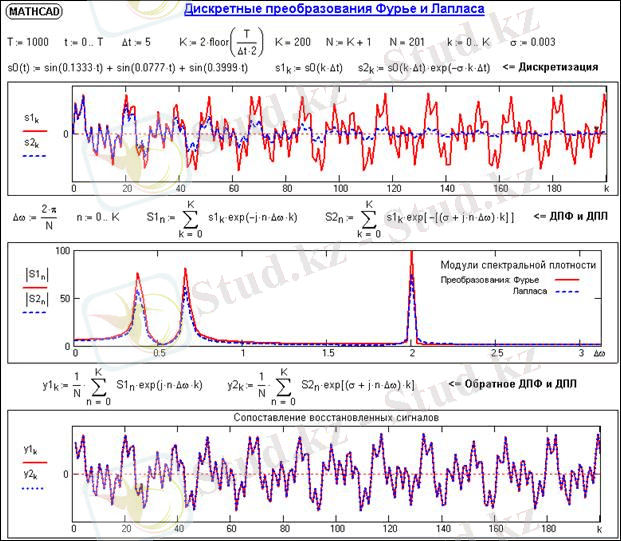
2 - сурет. Лаплас пен Фурье түрленуінің салыстырымы.
Казуальді дабылдың оң жақ интегралы Фурье түрленуін көрсетеді, y'(t) дабылдың экспоненциалды көбейткіші арқылы exp(-st) таңдауы s>0 -ге өшкен және соңғы энергия бойынша айналады. Барлық қасиеттер және Фурье түрленуінің теоремалары сәйкес аналогқа ие және Лаплас түрленуі.
2. 1 Фурье түрленуі
Дискретті Фурье түрленуі аргументтің Дискреттеу интегралының түрленуімен тікелей алынуы мүмкін (t k = kDt, f n = nDf) :
S(f) =
 s(t) exp(-j2pft) dt, S(f
n
) = Dt
s(t) exp(-j2pft) dt, S(f
n
) = Dt
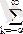 s(t
k
) exp(-j2pf
n
kDt)
s(t
k
) exp(-j2pf
n
kDt)
s(t) =
 S(f) exp(j2pft) df, s(t
k
) = Df
S(f) exp(j2pft) df, s(t
k
) = Df
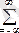 S(f
n
) exp(j2pnDft
k
)
S(f
n
) exp(j2pnDft
k
)
Уақыт бойынша Дискреттеу функциясы спектрдің периодтылығынна алып келеді, ал жиілік бойынша спектрдің дискретизацисы - функция периодтылығына алып келеді. Сонымен қоса ұмытпауымыз керек (8. 1. 1) сандық қатардың S(f n ) -ы функцияның үзіліссіз Дискреттеу S'(f) функцияның дискретті спектрі s(t k ), тура (8. 1. 2) санды қатардың мәніне тең s(t k ) үзіліссіз функцияның Дискреттеу болып келеді s'(t), және қайта қалпына келген кезде үзіліссіз функция S'(f) және s'(t) дискретті есептеуге сәйкес S'(f) = S(f) және s'(t) = s(t) Котельников-Шеннон теоремасының жүзеге асуында ғана кепіл болады.
Дискретті түленулер үшін s(kDt) Û S(nDf), және функция, және оның спектрі дискретті және периодты, ал сандық массивтер негізгі периодтардың берілуіне сәйкес Т = NDt ( 0-ден до Т-ға дейін немесе Т/2-ден Т/2-ге дейін), және 2f N = NDf (f N -ден f N -ге дейін), мұнда N - есептеу саны, бұдан:
Df = 1/T = 1/(NDt), Dt = 1/2f N = 1/(NDf), DtDf = 1/N, N = 2Tf N.
байланысы динамикалық және жиілікті формадағы дискретті дабылдар ақпаратты шартпен тең бағалылы болып келеді. Басқалай айтқанда: функция есептеудің саны және оның спектрлері ұқсас. Бірақ әрбір комплексті спектрді есептеу екі заттай санды көрсетеді, және соған сәйкес копмлексті спектрді есептеу саны функция есептеуінен 2 есеге үлкен. Ол солай. Бірақ спектр көрінісі комплексті формада - спектральді функцияның математикалық көрінісі, нақты есептеулер екі комплексті есептеудің түйіндестерінің қосылуынан құрылады, ал функция спектрі туралы толық ақпарат комплексті формамен тек бір жағынан тұжырымдалады - шын есептеулер және жалған бөліктің комплексті сандарыныі жиілікті интервалда 0ден f N -ге дейін, себебі ақпараттың екінші бөлігі 0ден -f N -ге дейін диапазонда бірінші бөлікпен түйіндес және қосымша ақпаратты жеткізбейді.
Дискретті көрініс кезіндн дабыл аргументі t k әдетте k сандарымен қойылады (берілгені бойынша Dt = 1, k = 0, 1, …N-1), ал Фурье түрленуі n аргумент бойынша жүзеге асады (жиілік бойынша қадам саны) негізгі периодтарда. N мәні кезінде, 2 еселік:
S(f
n
) º S
n
=
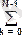 s
k
exp(-j2pkn/N), n = -N/2, …, 0, …, N/2.
s
k
exp(-j2pkn/N), n = -N/2, …, 0, …, N/2.
s(t
k
) º s
k
= (1/N)
 S
n
exp(j2pkn/N), k = 0, 1, …, N-1.
S
n
exp(j2pkn/N), k = 0, 1, …, N-1.
Спектрдің негізгі периоды (8. 1. 4) -те циклдық жиілікте -0, 5- ден 0, 5 -ке дейін, бұрыштық жиілік -p - ден p ге дейін. Жұп мәнде N шегі негізгі периодты жиілік бойынша ( ±f N мәні) жиілік бойынша есептеуде жарты қадамда орналасқан ±(N/2) және, осыған сай, жоғарғы шектің қосылуы N/2-ге тең болып орналасады.
Еспетеу операцияларында ЭЕМ -да теріс жиілікті аргументтерден басқа (n санынң теріс мәні) және бірдей алгоритмдердің тура және кері Фурье түрленулердің қолданулары 0 -ден 2f N -ға дейінгі интервалда қабылданады, ал соммалану (8. 1. 5) -те 0 де N-1-ге дейін сәйкес жүзеге асады. Осыдан ескеру керек, комплексті түйіндес есптеуде S n * интервалы(-N, 0) екіжақты спектрдің интервалында 0-2f N S N+1-n есептеуіне сәйкес (яғни түйіндес есптеулер 0-2f N инетрвалында S n және S N+1-n есептеуі болады ) .
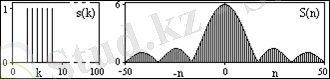
2. 1 - сурет
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz