Мектепте матиматиканы үйретудің жалпы мақсаттары

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 116 бет
Таңдаулыға:

Жоспар

1. Геометриялык фигураларды ажырату, қарапайым салуларды орындау.

2. Геометриялық шамаларды өлшеу және геометриялық фигуралардың периметрін, ауданын және көлемін есептеп табу құзыреттіліктерін қалыптастыратын геометрия элементтерін кезеңдер бойынша оқыту технологиясы.

1. Дәстурлі әдістеме салу есебін шешуді - анализ, синтез (салу), делелдеу және зерттеу -төрт кезеңге бөлуді ұсынады. Алайда есепті шешудің дәстүрлі схемасының (жолының) қандайда кезеңі жиірек түсіп қалады, мәселен, көбінесе «дәлелдеу» кезеңіне ерекше көңіл бөлінбейді. Осы тұрғыдан мысал ретінде «қабырғалары а және в тік төтбұрыш салу»есебін қарастырайық. .

Геометриялық салулардың қарапайым есептеріне мыналар жатады; берілген түзуге (берілген кесіндіге) параллель және перпендикуля болатын түзулерді салу; бұрыштардың салу; кесінділерді салу ; шеңберді және оның доғаларын салу; щеңберге жүргізілген жанамаларды салу; көпбүрышты сырттай сызылған шеңбірді салу және шеңберге іштей сызылған көпбұрышты салу көпбұрышқа іштей сызылған шеньерді салу және шенберге сырттай сызылған көпбұрышты салу; үшбұрыштарды салу студенттердің жеке өзіндік жүмысына арналған тапсырма. Салу есептерінде «бұрыш берілген» және «кесінді берілген» деп жиі айтылады. Бұл сөздер кесіндінің (сәйкес пүрде бұрыштың ) сандық мәні емес, геометриялық кескіні берілгендігін білдіреді. Салу есептерін орындаған кезде мынаны да еске алу керек; кейбір геометриялық фигураларды салу есебі белгілі бір дәрежедегі дәлдікті сақтай отырып практика жүзінде фигура сызу емес, біздің құралдарымыз салудың абсалют дәлдігін қамтамасыз етеді деп, сызғыш пен циркуль көмегімен қажетті салудың теориялық тұрғыдан қалай орындалатынын анықтау.

Бастауыш сыныпта математиканы оқытуда геометриялық мазмұнды есептер қарастырылады. Мысалы, тіктөртбұрыштың периметрін былайша табуға болады: оның еніне ұзындығын қосып, екіге көбейтуге болады. Квадратта барлық қабырғалары тең. Сондықтан оның периметірі 4 еселенген ұзындығына тең болады. Көпбұрыштың периметірі латынның Р әріпімен белгілейді.

Р= 4+4+8+8=24(см)

Р= (4+8) *2=24 (см)

Шаршының периметірі: Р=8*4=32(см)

Кесінді жайында түсінік беру және оларды басқа фигуралардан ажыратуды үйрету, кесінді салудың ерекшелігімен таныстыру.

Геометриялық шамалар жайындағы, әсіресе «ұзындық» пен «аудан» туралы оқушылар білімдері әр алуан мақсатта қолданылатын материалдың қатарына жатады. Сондықтан олар жайындағы түсініктің дұрыс қалыптасуына және сәйкес ұғымдарды практикалық мақсатта қолдануға оқушыларды жеткілікті машықтандыруға курста қолайлы жағдайлар жасалған. Оның ең негізгісі - фигура периметрі мен ауданын оқытып үйрету . Мәселен, алдымен ұзындық және аудан сияқты шамалардың бола алатынын оқушылар практикалық жұмыстар нәтижесінде (кесінділерді, әр түрлі жазық фигураларды салыстыру) түсінеді, сонан кейін шаманың өлшем бірлігі (1 см, 1 см ² ) енгізіледі, әрі қарай оқушылар шаманы өлшеудің негізгі тәсілін игереді, ең соңында шаманың басқа да өлшем бірліктерінің арасындағы қатыстар тағайындалады.

2. Тік төртбұрыш пен шаршының аудандарын табу ережелерімен таныстыру.

а) Дайындық әр түрлі тәсілмен есептеу қажет : тік төртбұрыш неше шаршыдан тұрады?

Қатар бойында : 5 шаршыдан 4 қатар - 5 · 4 = 20 (шаршы)

Баған бойынша : 4 шаршыдан 5 баған - 4 · 5 = 20 (шаршы)

Тік төртбұрыштағы шаршылар санын оқушылар өз беттерімен әр түрлі тәсілмен сынайды: 8 · 3 = 3 · 8 = 24

ә) Тік төртбұрыш пен шаршының аудандарын табу.

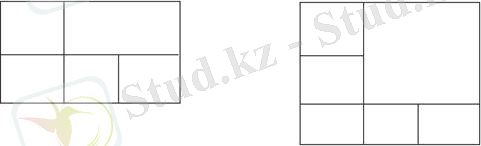
1 см ²

Бір бағанда неше квадрат сантиметр бар? (екі) Осындай тағы неше баған бар? (үш) Тік төртбұрыштың қабырғалары 1 см-ден неше тең бөлікке бөлінген? (екі және үш) . Оның ауданын табу керек: 2 · 3 = 6 см ² , (шаршымен де осыған ұқсас) 3 · 3 = 9 см ² .

Әр фигураның қабырғалары неше сантиметрді құрайды?

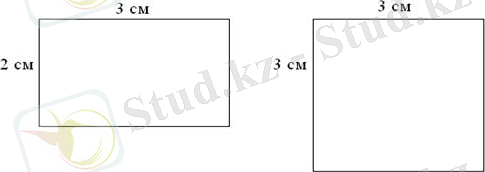
Тік төртбұрыш : 2 см және 3 см.

Шаршы: 3 см және 3 см.

Фигураның қабырғаларын 1 см-ден неше тең бөліктерге бөлуге болады? (2-ге және 3-ке; 3-ке және 3-ке) . Әр фигурада неше квадрат сантиметр баған бар? (3 бағаннан) . Әр фигураның ауданын тап: 2 · 3 = 9

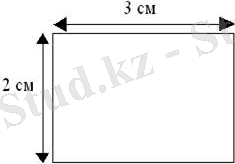
2 см тік төртбұрышта екі қатар квадрат сантиметр бар екенін көрсетеді; 3 см тік төртбұрышта үш баған квадрат сантиметр бар екенін көрсетеді, демек, тік төртбұрыштың ауданы 2 · 3 = 6 см ²

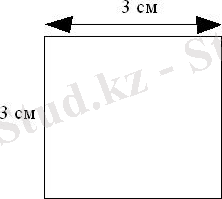
3 см шаршыда үш және үш баған квадрат сантиметр бар екенін көрсетеді, демек, шаршының ауданы 3 · 3 = 9 см ² .

б) Шаршы мен тік төртбұрыштың периметрін және ауданын әр түрлі тәсілдермен табуды салыстыру:

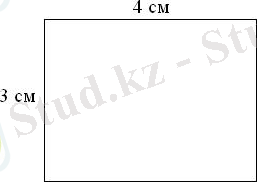
Периметр: Аудан:

І. 3 + 4 + 3 + 4 = 14 І. 3 · 4 = 12

ІІ. 3 · 2 + 4 · 2 = 14 ІІ. 4 · 3 = 12

ІІІ. (3 + 4) · 2 = 14

Жауабы : 14 см. Жауабы : 12 см ² .

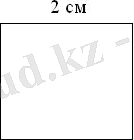
Периметр: Аудан:

І. 2 + 2 + 2 + 2 = 8 І. 2 · 2 = 4

ІІ. 2 · 4 = 8

Жауабы: 8 см. Жауабы: 4 см ²

в) Тік төртбұрыштың және шаршының ауданын табу ережелерімен таныстыру:

Тік төртбұрыштың ұзындығы 4 см, неі 2 см. Тік төртбұрыштың ауданы

4 · 2 = 8 см ² немесе 2 · 4 = 8 см ²

Ереже: Тік төртбұрыштың ауданын табу үшін оның бірдей өлшеммен берілген ұзындығын еніне көбейту керек.

Бақылау сұрақтары

1. Геометриялық салуларға мысалдар келтір.

2. Геометриялық мазмұнды есептер түрлерін ата.

3. Геометриялық мазмұнды есептермен жұмыс істеу әдістемесін көрсет.

Әдебиеттер:

1. Оспанов Т. К., Кочеткова О. В., Астамбаева Ж. Қ. Жаңа буын оқулықтары бойынша математиканы оқыту әдістемесі. 1-4-сыныптар. - Алматы: «Атамұра», 2005.

2. Т. Қ. Оспанов, Ш. Х. Құрманалина, С. К. Құрманалина. Бастауыш мектепте математиканы оқыту әдістемесі. - Астана, «Фолиант», 2007.

3. Кдырбаева А. А. и др. Внеклассная работа по математике в начальной школе. - Алматы, 2000.

4. Астамбаева Ж. Қ. Бастауыш мектепте математиканы оқыту теориясы мен технологиясы. (Практикалык, лабораториялық сабақтар, СОӨЖ) . - Алматы, 2008.

Жоспар

1. Қарапайым геометриялық салулар; геометриялық мазмұнды есептер.

2. Геометриялық шамалар (фигураның периметрі, ауданы мен көлемі) және көпбұрыштардың периметрлерін, тік төртбұрыштың (шаршының) ауданын, тік бұрышты параллелепипедтің (текшенің) көлемін есептеп табу.

1. Геометриялық фигураларды салу « бір жақты » сызғыш циркуль көмегімен орындалады. « Бір жақты » сызғыш дегеніміз бір ғана істі орындау үшін, яғни берілген екі нүкте арқылы түзу жүргізу үшін қолданылатын құрал. Циркуль дегеніміз - шеңбер салу үшін және берілген кесіндіні түзу бойында геометриялық жолмен салу үшін қолданылатын құрал. Алайда басқадай да құралдар көмегімен орындалатын саулар болады. Мысалы: тек қана циркуль арқылы Моро - Маскерони салулары тек қана сызғыш арқылы, егер де жазықтықта шеңбер және оның центрі сызулы болса, тек қана жиектері пааллель сызғыш арқылы, тек қана сүйір бұрыштың көмегімен және т. б құралдары арқылы орындалатын салулар.

2. Аудан - жазық нәрселердің қасиеті ретінде олардың басқа қасиеттерінің арасынан ажыратылып көрсетіледі. Тіпті мектеп жасына дейінгі балалар нәрселердің аудандарына қарап салыстырады және салыстырылатын нәрселер бір -бірінен айрықша, өзгеше немесе мүлдем бірдей болса, «көп», «аз» «тең, бірдей» қатынастарын дұрыс тағайындайды. Мұнда балалар нәрселердің бірінің үстіне бірін қойып өлшеуді сирек пайдаланады, нәрселерді үстелдің үстінде, жерде, бір парақ қағаз бетінде т. с. с. алып тұрған орнына қарай салыстыра отырып, олардың көз мөлшерімен салыстырады. Мысалы, қайын жапырағы үйеңкі жапырағынан кіші, біздің үйдің жанындағыға қарағанда, мектептің жанындағы мұз айдынын үлкен, барлық құймақ - үлкен де емес, кіші де емес, бірдей т. б.

Ауданды оқыту әдістемесін қарастырайық:

1. Фигураның ауданымен таныстыру.

а) Дайындық : бірінші сыныпта оқушылар геометриялық фигуралармен танысады:

Фигураны бөліктерге бөлу және фигураны бөліктерден құрастыру.

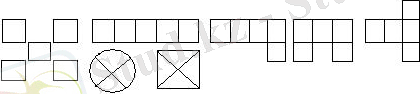
Дамытушылық сипаттағы тапсырмалар ұсынылады: неше фигура берілген?

Фигураларды түрлендіру :

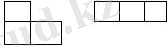
Бір шаршы қалатындай бір таяқшыны ал. Тағы қандай фигуралар қалады?

Екінші сыныпта жұмыс жалғастырылады.

Үшінші сыныпта аудан ұғымы еңгізіледі: әр түрлі фигуралар көрсетіледі де, оқушылар қай фигура көп орын алтынын анықтайды.

Ол үшін тақтаға әрбір фигураның контурын салып, қортынды шығарту қажет: әр фигура тақта бетінің қандай да бөлігін алады, ол аудан делінеді.

Одан кейін фигуралардың аудандары салыстырылады: алдымен «көз мөлшерімен» содан соң салыстыру нәтижесі беттестіру арқылы тексеріледі.

Фигураларды беттестіргенде, олар толығымен бір-бірімен беттесе, онда олардың аудандары бірдей.

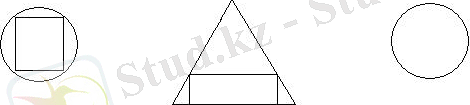
Егер бір фигура екіншісінің ішінде толығымен жататын болса, онда бірінші фигураның ауданы екіншісінен кіші болады (және керсінше) .

Беттестіру арқылы салыстыру тәсілі әрқашан да орындала бермейтінін көрсету кажет.

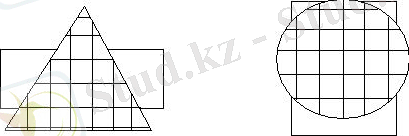
Ешбір фигура толығымен екінші біреуінің ішінде ешқандай да жағдайда жатпайды.

Аудандары бірдей фигураларды табу мүмкін емес, өйткені оларды бір-бірімен беттестіруге болмайды.

Фигураның бірдей шаршыларға, яғни шартты өлшеуіштерге (см ² еңгізуге дайындық) бөлу.

Әр фигура неше шаршыдан құралғанын санау және олардың аудандарын салыстыру: шаршыларының саны артық фигураның ауданы артық .

көрсету (әр балада осындай модель бар) : осы шаршының қабырғаларының ұзындықтарын өлшеу - 1 см, осыдан мынадай анықтама жасауға болады: « Қабырғаларының ұзындығы 1 см-ге тең шаршы квадрат сантиметр деп

аталады ».

1 см ² жазуды көрсету - бұл аудан бірлігі.

Оқушылар шатастырып алмас үшін сызықты және квадраттық өлшеу бірліктерін салыстыру.

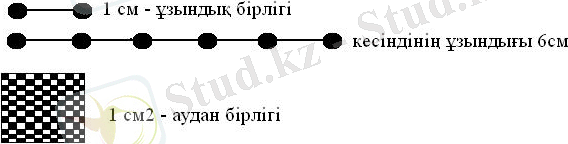
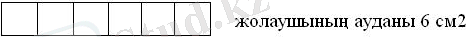
2. Ауданды өлшеу бірліктерін қалыптастыру.

а) 1 см ² моделін пайдаланып, оқушылар әр түрлі геометриялық фигуралар құрастырады және олардың аудандарын қайсысында квадрат сантиметрлер артық (кем) болса, сол фигураның ауданы артық (кем) болатынын айтады.

9 см ² 6 см ²

ә) Фигураның ауданы оны квадрат сантиметрлерге бөлу арқылы табылатындығын хабарлау. Әр фигураның ауданы неге тең? Аудандары бірдей фигура бар ма?

б) Квадрат сантиметрлерге бөлінбейтін - еркін пішіндегі дөңгелектер, сопақшалар сияқты фигуралар көрсетіледі; толық емес шаршылар шығады.

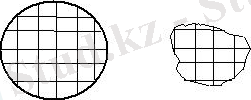
в) Еркін пішіндегі фигуралардың аудандарын өлшеуге арналған арнайы құрал көрсетіледі - ол палетка деп аталады - квадрат сантиметрлерге бөлінген мөлдір пластина (10х10) . Ауданды өлшеу үшін ол фигураның үстіне салынады.

г) Палетканы қолдану тәсілі және ауданды есептеу үлгісі көрсетіледі :

толық шаршылар санына толық емес шаршылардың жартысы қосылады - бұл фигураның ауданы, мысалы, 9 см ² + 16 см ² : 2 = 9 см ² + 8 см ² = 17 см ² .

3. Тік төртбұрыш пен шаршының аудандарын табу ережелерімен таныстыру.

а) Дайындық әр түрлі тәсілмен есептеу қажет : тік төртбұрыш неше шаршыдан тұрады?

Қатар бойында : 5 шаршыдан 4 қатар - 5 · 4 = 20 (шаршы)

Баған бойынша : 4 шаршыдан 5 баған - 4 · 5 = 20 (шаршы)

Тік төртбұрыштағы шаршылар санын оқушылар өз беттерімен әр түрлі тәсілмен сынайды: 8 · 3 = 3 · 8 = 24

І. (2 · 2) · 5 = 20 см ²

ІІ. 2 · (2 · 5) = 20 см ² - шаршыладың ауданы.

г) Үшбұрыштың (тік бұрышты) ауданы туралы түсінік.

Осындай екі үшбұрыштан тік төртбұрыш құрастыр.

Оның ауданын тап: 4 · 3 = 3 · 4 = 12 см ² .

Осы үшбұрыштың ауданы туралы не айтуға болады? (Оның ауданы тік бұрышты төртбұрыштың ауданының жартысына тең) .

4 см және 3 см => (4 · 3) : 2 = 12 : 2 = 6 см ² .

ғ) Күрделі фигуралардың аудандарын оларды қарапайым геометриялық фигураларға бөліп, ереже бойынша аудандарын табу арқылы табу.

S = S _ٱ + S _∆ = 16 + 6 = 22 см ²

Тақырыбы: «Геометрия элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы.

Жоспар

1. «Геометрия элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы.

2. Желінің негізгі нысандары: қарапайым геометриялық фигуралар, олардың қасиеттері мен белгіленуі.

1. Бастауыш сыныптарда геометриялық материал бөлек тақырып болып қарастырылмайды. Геометриялық материал арифметикалық және алгебралық материалдарымен тығыз байланыста қарастырылады. Бастауыш сыныпта: кеңістік туралы түсінік, нақты фигура туралы ұғым, геометриялық фигуралармен байланысты қарапайым ұғымдар, оларды ажырату, геометриялық шамаларды өлшеу, фигураларды салудың бастама білігін қалыптастыру, әртүрлі геометриялық шамалармен таныстыру қарастырылады да, оқушылар геометриялық алғашқы түсінтерді жинақтайды әрі дамытады, кейбір геометриялық терминдермен танысады; қарапайым сызу және өлшем құралдарын пайдалан біліудің қарапайым дағдыларын меңгереді.

Бастауыш сыныпта қарастырылатын мазмұнды жаттығулар мен есептер жүйесі және олармен жұмыс істеу әдістемесі балаларда кеңістік ұғымының, бақылау, салыстыру, абстракциялау және жалпылау біліктерінң дамуына ықпал жасауға тиіс.

Геометриялық фигуралар тек оқытудың мақсатын ғана емес, оқытудың құралы да геометриялық материалдар сандардың реттік қатары, арифметикалық амалдар тексті есептер, үлес сияқты мәселелерді оқыту барысында көрнекі құрал ретінде пайдаланылады;

Геометриялық ұғымдарға (тік төртбұрыштың, шаршы және периметрдің басқаларына) анықтама тек қана остенсивті түрде көрсету арқылы беріледі;

Геометриялық материалдар оқушылардың ойлау қабілетін дамыту үшін де пайдаланылады;

Геометриялық материалдар оқушыларға математика мен өмір байланысын түсінуге есептігін тигізеді;

Геометриялық материалдар оқушыларда практикалық іскерліктер қалыптастырады.

Геометриялық материалды оқып үйренудің неғұрлым тиімді әдісі болып табылатын мына сияқты лаборатория- практикалық әдістер: қағаздан, таяқшалардан, сымнан фигуралардың модельдерін жасау; сызу, өлшеу т. б. Мұнда елеусіздеу белгілерін(түсі, өлшемі, жазықтықта орналасуы т. б. ) өзгертіп ала отырып объектілердің алуан түрлілігін қамтамасыз етудің, балаларға елеулі белгілерін-нәрселердің формасын, фигуралардың қасиеттерін т. б. айырып көрсете білуді меңгеру мен көмек берудің маңызы зор.

Геометриялық түсініктер мен ұғымдарды өздігінен және мейлінше айрықша бағытта ұсына отырып, орындалатын болса да мүмкін болатын жерде сабақта геометриялық материалдарды оқып үйрену арифметикалық және алгебралық материалды оқып үйренумен байланыстырылуы тиіс.

Тақтадан сызбаларды орындау үшін сыныпта сызба-өлшеуіш аспаптар жиынтығының: сызығштың, сызба үшбұрышының, циркульдің болуы қажет.

Мектепте оқу - тәрбие үрдісін ұйымдастыруда қазіргі кезде өзара байланысты екі мақсат көзделеді:

Оқушылардың ойлау қабілетін дамыту және өз бетімен білім алу ынтасын тәрбиелеп, оның жолдарын үйрету.

Оқушылардың шығармашылық қабілеті мен ойлау шеберліктерін тек ізденумен проблемаларды өз бетінше шеше білуді үйретумен жетілдіруге болады. Мұндай ізденуді іске асыруда оқушыларға тыңғылықты білім беруде проблемалы оқытудың маңызы зор.

Бастауыш сыныптарда геометриялық материалды оқып үйренудің негізгі міндетттері:

1. Оқушылардың нүкте, түзу сызық, түзу кесінді, сынық сызық, бұрыш, көпбұрыш, дөңгелек сияқты геометриялық фигуралар туралы айқын

түсініктерін және алғашқы ұғымдарын қалыптастыру;

2. Геометриялық фигуралар: сызықтар (түзу, қисық, тұйықталған, тұйықталмаған, сынық сызықтар, перпендикулярлар және пареллельдер) ; нүкте, сәуле, бұрыш, кесінді, көпбұрыштар: үшбұрыш, төртбұрыш, тік төртбұрыш, шаршы; олардың элементтері (төбелері, бұрыштары, қабырғалары) ; сопақша, дөңгелек, шебер және олардың элементтері (центрі, радиусы, диамтері) туралы нақты түсінік қалыптастыру.

3. Ұзындық жөнінде нақты түсінік қалыптастыру және заттың ұзындығын салыстыру, кесіндінің ұзындығын өлшеу сияқты ұғымдарды меңгеру.

4. Ұзындықтың өлшемі бірліктерімен: сантиметр, дециметр, метр, километр, миллиметр және олардың арасындағы қатынаспен таныстыру.

5. Сызғыштың көмегімен кесіндінің ұзындығын өлшеу, сондай - ақ берілген ұзындық бойынша кесінділер сызу, кесіндінің ұзындығын кеміту немесе арттыру, кесінділерді ұзындықтарына қарай салыстыру біліктерін түрлендіру (іріден ұсаққа және керісінше) ; әр түрлі бірліктермен берілген ұзындықты салыстыру, сондай - ақ шамалармен ( ұзындық ) амалдар

орындауға үйрету.

6. Ұзындық бірліктерін түрлендіру (іріден ұсаққа және керісінше) ; әр түрлі бірліктермен берілген ұзындықты салыстыру, сондай - ақ шамалармен (ұзындық) амалдар орындауға үйрету.

7. Фигураның ауданы туралы түсінік беру және фигураның ауданын салыстырудың әр түрлі тәсілдерімен таныстыру.

8. Аудан бірліктері: см ² , дм ² , м ² , мм ² , ар, гектармен таныстыру. «Палетканың» көмегімен фигураның ауданын табуға үйрету.

9. Аудан бірліктері арасындағы қатынасты игеру және шамаларды түрлендіруге, салыстыруға және аудан бірліктерімен амалдар орындауға үйрету.

10. Тік төртбұрыш, шаршы, сондай-ақ әлдеқайда күрделі фигуралардың аудандарын табуға үйрету.

11. Қарапайым кеңістік денелерімен: текше және тік бұрыштары параллелепипед; олардың элементтері: төбелері, жақтары, қырларымен таныстыру.

12. Геометриялық фигураларды өлшеу және оларды «көз мөлшерімен», «еркін өлшеммен қолмен» салу, құралдардың: сызғыш, траспортир, циркульдің көмегімен, сызықтары бар және сызықсыз қағазды салу, практикалық біліктерге жаттықтыру.

13. Кесіндінің қосындысы мен айырмасын, көпбұрыштардың периметрі мен ауданын, текшенің және тік бұрышты параллелепипедтің көлемін табуға үйрету.

14. Геометриялық фигураларды түрлендіруге үйрету.

2. Геометрия элементтерін оқытып үйретудің басты және аса маңызды нәтижесі - фигураларды бір-бірінен ажырату және оларды тани білу іс-әрекетін меңгеру. Ол оқу процесінде, әсіресе, геометриялық мазмұнды жаттығулар мен материалдарды қарастыру барысында жүзеге асырылады. Дегенмен, бастауыш буынның соңын ала осындай іс-әрекеттер түрлерін арнайы қайталау, тиянақтау, жетілдіру, қорытындылау, бір жүйеге келтіру бағытында арнайы жұмыстар ұйымдастырудың тиімділігін тәжірибе көрсетіп отыр. Алайда, төрт жылдық бастауыш мектептін соңына қарай берілетін қайталауға арналған жаттығулардың ішінде геометриялық мазмұнды тапсырмалар жетеу-ақ (10) . Олардың өзі дәстүрлі мәселелерді (периметр мен ауданды есептеу және салыстыруды, кыадрат пен тік төртбұрышты салуды) қайталауға арналған. Әрине, бұл мәселелер өзінің дидактикалық құнын жойған жжоқ, дегенмен, олар бағдарламада анықталған негізқгі геометриялық іс-әрекеттерді оқушылардың тиянақты меңгеруін қамтамасыз ете алмайды. Сондықтан негізгі геометриялық іс-әрекеттерді тиянақтала, жетіле, дами түсуіне себепші болатын және бастауыш буынының соңын ала арнайы өткізілетін қайталау сабақтарында қарастырылуы тиісті жаттығуларды келтірейік.

Бірінші топтың жаттығулары ажырату және танып білу іс-әрекеттерінің орындалуын көздейдді. Мұнда оқушылар жаттығуларды орындау барысында фигуралардың бірнеше қасиеттерден тұратын сипаттамалық белгілерін еске түсіреді және оларды айтып шығады, әрі қарай сол қасиеттер фигураға тәне екенін біртіндеп тағайындап, тексеруден өткізеді, сонан кейін әрбір фигураның қарастырып отырған ұғымға тиісті немесе тиісті емес екендігі жайында қорытынды жасайды.

1) Суретті қараңдар:

Көпбұрыш, үшбұрыш, төртбұрыш, тік төртбұрыш, шаршы, тік бұрыш, тік емес бұрыш болатын фигуралардың сәйкес нөмірлерін теріп жазыңдар.

2) Суретті қараңдар:

Әрббір фигураның сәйкес «атын» келтіріңдер.

3) Суретті қараңдар:

Барлық тік бұрыштардың, көпбұрыштардың, шаршының сәйкес нөмірлерін теріп жазыңдар.

4) Суретті қараңдар:

Барлық тік төртбұрыштарддың, шаршының сәйкес нөмірлерін теріп жазыңдар.

5) Суретті қараңдар:

Барлық тік бұрыштардың, тік емес бұрыштардың сәйкес нөмірлерін теріп жазыңдар.

6) Суретті қараңдар:

Барлық төртбұрыштардың, тік төртбұрыштардың, шаршылардың сәйкес нөмірлерін теріп жазыңдар.

7) Суретті қараңдар:

Әрбір фигураның сәйкес атын келтіріңдер. Әрбір суретте қанша кесінді бар?

8) Суретті қараңдар:

Әрбір үшбұрыштың, тік төртбұрыштың сәйкес белгіленуін жазып көрсетіңдер. Әрбір фигураны белгілеп көрсету үшін қанша әріп пайдаланылған? Неліктен?

Сызбаны қараңдар:

Сызбадан барлық көпбұрыштарды табыңдар және оларды қалай аталатынын жазып көрсетіңдер.

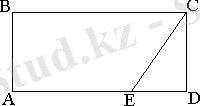
Екінші топтың жаттығулары геометриялық фигуралардың бейнелерін еске түсіруді көздейді.

1. Кез келген үшбұрыш, төртбұрыш, шаршы, кесінді, тік емес бұрыш, көпбұрыш сызыңдар.

2. Кез келген үшбұрыш сызыңдар. Оның төбелерін әріптермен белгілеңдер де, қалай аталатынын жазып көрсетіңдер.

3. Кез келген тік төртбұрыш сызыңдар. Оның төбелерін әріптермен белгілеңдер де, қалай аталатыын жазып көрсетіңдер.

4. Кез келген кесінді сызыңдар, оның ұштарын әріптермен белгілеңдер де, қалай аталатынын жазып көрсетіңдер.

Үшінші топтың жаттығулары сызу дағдыларын қалыптастыруға және тиянақты түсуге арналады. Сонда әр түрлі жағдайларда геометриялық фигураларды салудың ерекшеліктері пысықталады.

1. Кез келген шаршы салыңдар.

2. Қабырға 3 см шаршы салыңдар.

3. Кез келген кесінді салыңдар.

4. Ұзындығы мынадай кесінді салыңдар: 5 см, 1 дм, 2 см.

5. Кез келген тік төртбұрыш салыңдар.

6. Іргелес қабырғалары 2 см және 3 см тік төртбұрыш салыңдар.

Осы тапсырманың қайсысын орындағанда болсын, алдымен сәйкес фигураның сипаттамалық белгілері мен қасиеттері еске түсіріледі де, әрі қарай фигура қалауымызша алынған өлшем бойынша немесе берілген шарттарға сәйкес салынады.

Төртінші топтың жаттығулары оқушылардың геометриялық шамалар, оларды өлшеу және есептеп шығару жайындағы білімдерін бір жүйеге келтіреді және қорытындылайды.

1. Сызбаның берілгендерін пайдалынып, фигураның периметрін табыңдар: