Ағындар бұрылған, бөлінген және тоғысқан кезде аэродинамиканың кедергі коэффициенттерін өлшеудің аспаптары мен әдістері

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Кіріспе

Жергiлiктi кедергiге ағынның формасының кенеттен өзгеруі (жергiлiктi), жəне сыртқы шекара бағытының ауысыуы (шұғыл кеңею, тарылу мен бұрылу, желдетіс терезесі, қазбаның тарамдалу орны, кроссингiлер, желдетіс арналары т. б. ) жатады

Жергiлiктi кедергi нысандарының қосынды кедергi күшi, олардың салыстырмалы орналасуымен өзара қашықтығына тəуелдi.

Жергiлiктi кедергi нысандарының өзара қашықтығы ағынның деформация дəрежесiмен келесi кедергiге кiруiндегi оның шекаралық қабатын қалпына келуiн анықтайды. Деформацияланған жылдамдық өрiсiнiң толық қалпына келуi жергiлiктi кедергiден кризистiк қашықтықта жүредi. Егер екi кедергiнiң өзара қашықтығы кризистiк қашықтықтан кiшi болса, онда екiншiсiнiң бiреуi табылған орында, құйындау қарқыны мен кедергi шамасы аз болады.

Ағындар бұрылған, бөлінген және тоғысқан кезде аэродинамиканың кедергі коэффициенттерін өлшеудің аспаптары мен әдістері

Массаның сақталу заңы . Ауаның қозғалу заңына орай бұл заңды былай тұжырымдауға болады: ауаның бiртектi бөлшектен тұратын кез келген көлемiнiң массасы, оның қозғалысы кезiнде тұрақты болып қалады. Яғни, массаның уақытқа байланысты өзгерiсi нөлге тең. Егер ауа ағынындағы, тұрақты тығыздығы бар ауаның элементар көлемiн бөлiп көрсетсек, онда масса сақталу заңы былай өрнектеледi:

$dM/dt\ = \ 0\$

мұнда, М - бөлiнген көлемдегi ауа массасы; t - уақыт.

Бұл теңдеудегi ағын жылдамдығының координат осьтерiне проекциясы мына түрде болады:

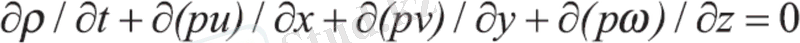(6. 4)

мұнда, u , υ, ω - ағын жылдамдығының координат осьтегi проекциясы.

(6. 4) өрнегi ағынның үздiксiздiгiнiң теңдеуi деп аталады. (6. 3) теңдеуiнен уақыт бойынша толық алынған туындысымен (6. 4) теңдеуiнен уақыт бойынша дербес алынған туындысында айырма болады. Толық туынды дифференциалданатын шаманың уақыт бойынша даму үдерісімен кеңiстiктегi қарастырылып отырған көлемнiң қозғалысын есепке алса, ал дербес туынды кеңiстiктегi көлемнiң орын ауыстыру өзгерiсiн есепке алмайды. Ағын сипаты (тығыздық, жылдамдық, қысым, т. б. ) стационар қозғалыс (қалыптасқан) үшiн кеңiстiктегi кез келген бiр бекiтiлген нүктеде уақыт бойынша өзгермейдi, = 0 да үздiксiздiк теңдеуi мынадай түрге келедi:

$\rho\ = \ const$ болғанда (6. 5) мына түрге келедi:

Қазбаның тұрақты қимасында: u = ω =0 (6. 6) болатындықтан, (6. 6) теңдеуiнен u = const екенiн табамыз. Яғни, ауа қозғалысының жылдамдығы ұқсас нүктеде тұрақты. (6. 6) теңдеуiнен көрiнетiндей бiр бағыттағы ағын жылдамдығының өсуi, оның басқа бағыттағы жылдамдығының кемуiне əкелуi керек, өйткенi теңдеудiң сол бөлiгiндегi мүшелердiң қосындысы, олардың мүшелерiнiң бiреуi терiс (ағынның баяулауы, ал қалғандарының оң (үдетiлген ағын) болғанда ғана нөлге тең болады. (6. 3) теңдеуiнен қазбадағы ауаның стационар қозғалысы үшiн аламыз:

М = const (6. 7)

Сонымен қазбадағы ауаның массалық шығыны тұрақты. Қазбадағы ауаның массалық шығынын келесі түрде өрнектейміз,

M = ρQ (6. 8)

мұнда, Q - ауаның қазбадағы көлемдiк шығыны. Онда изотермиялық (ρ=const) ағын үшiн (6. 7) өрнегiнен: Q = const

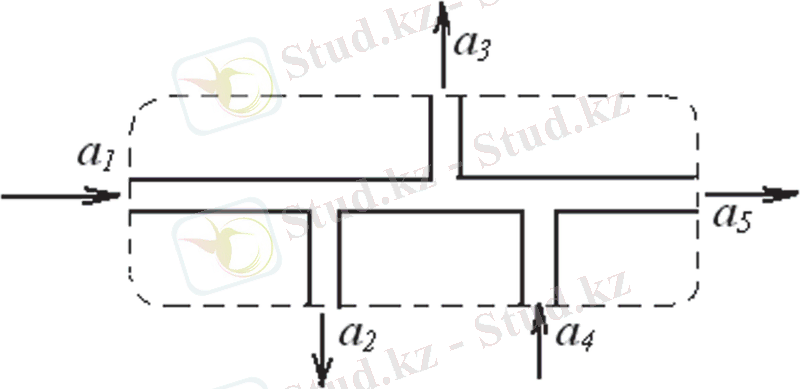
6. 2-сурет . Ауа ағыстарының таралу сұлбасы

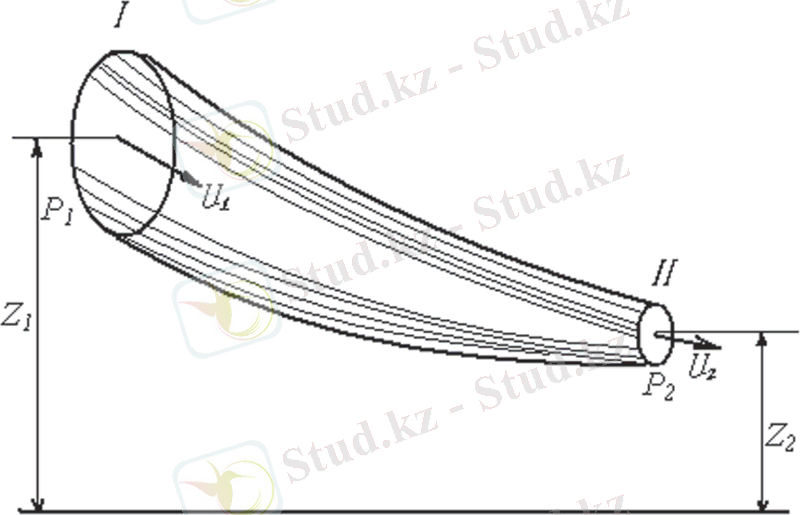
6. 3-сурет. Қазбадағы ауа ағыстарына байланысты

Бернулли теңдеуін шығаруға арналған сұлба

(6. 8) өрнегiнен (шығын теңдеуi деп те атайды) қазбадағы ағынның қозғалысы стационар болғанда ауаның көлемдiк шығыны тұрақты болады.

Ағынның тарамға бөлiнген жерiнде (6. 8) теңдеуi мына түрге

енеді:

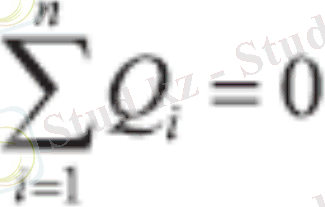(6. 9)

мұнда, і - ағын нөмірi; n - тарамдағы ағын саны.

6. 2-суретте көрсетiлген сұлба үшiн (6. 9) теңдеуi мына түрде өрнектеледi:

Q1 - Q2 - Q3 + Q4 - Q5 = 0

мұнда, 1, 2, 3, 4, 5 - ағындарындағы сəйкес Q1, Q2, Q3, Q4, Q5 ауа шығыны (оң таңбалы тарамға кiретiн ағын ол сол таңбалы шығатын ағын деп қабылданған) .

Қазбадағы ауа шығынын мына түрде жазайық:

Q = uSB (6. 10)

SВ - қазбаның көлденең қимасының ауданы (6. 8) бен (6. 10) өрнегiнен:

uSB = const (6. 11)

(6. 11) өрнегiнен қазба қимасы неғұрлым үлкен болса, онда одан өтетiн ауа жылдамдығы солғұрлым аз болатыны көрiнедi.

Энергияның сақталу заңы. Қозғалыстағы ауаға қолданатын бұл заң мына түрде баяндалуы мүмкiн: Қозғалыстағы ауаның белгiлi бiр уақыт аралығындағы кез келген көлемдегi энергиясының өзгерiсi, оған берiлетiн жылу энергиясымен ауаға түскен сыртқы күштiң жұмысының қосындысына тең яғни:

ΔEB+ΔEn+ΔEk= ΔQ+ΔA (6. 12)

мұнда, ΔEB - молекула қозғалысының кинетикалық энергиясымен оның потенциялық энергиясының өзара əсерiмен анықталатын қозғалыстағы ауаның iшкi энергия өзгерiсi; ΔEn - қозғалыстағы ауаның потенциялық энергия өзгерiсi; ΔEk - қозғалыстағы ауаның кинетикалық энергия өзгерiсi.

ΔQ - қозғалыстағы ауаның жылу энергиясының өзгерiсi. ΔА - сыртқы күштiң жұмысы. Қазбадағы ауа қозғалысына əсер ететiн сыртқы күш ауа қозғалысына кедергi келтiретiн күшпен (үйкелiс күшi) статикалық қысымнан тұрады.

ΔEB = ΔQ = 0 болатын адиабаттық ағын мен элементар ағынша қозғалысынан тұратын ауа ағыны өрнегiн (6. 12) келесі түрде өрнектеуге де болады:

dр + gρdz + d(ρu2) /2 +gρdh = 0 (6. 13)

мұнда, h - ауаның бiр өлшем салмағына тиесілі сыртқы күштiң

жұмысы.

(6. 13) өрнегiн дифференциальдық формадағы Бернулли теңдеуi (1738 ж осы теңдеудi тапқан Д. Бернуллидiң құрметiне орай) дейдi. (6. 13) өрнегiн қазбаның p =const кезiндегi I - ағынша қимасы бойымен II - ағынша қимасына дейiн интегралдап (6. 3-сурет) аламыз:

p1 - p2 + gρ(z1 - z2) + (ρ/2) (u - u ) = h (6. 14)

мұнда, p1, p2 I жəне II қимаға сəйкес келетiн ауаның статикалық қысымы: I жəне II қимаға сəйкес келетiн z1 жəне z2 қысымды ауа бағанының биiктiгi: u1, u2 - тиісінше I, II - қимадағы орташа жылдамдық.

Қазбадағы барлық ағын үшiн I жəне II қимада ауа тығыздығы

əртүрлi болғанда (6. 14) теңдеуi мынадай болады:

(p1 - p2) + g(ρ1z1 - ρ2z2) + [k1 (ρ1u /2) - k2 (ρ1u /2) ] = h (6. 15)

мұнда, k1, k2 - қазбаның I жəне II қимасындағы ауа жылдамдығын таралуының бiркелкi еместiгiн есепке алатын, кинетикалық энергия коэфицентi; h - ағынның I қимадан II қимаға орын ауыстырғандағы барлық сыртқы күштiң орындайтын жұмысы.

Дөңгелек штрек тəрiздi қазба үшiн,

k = 1 + 21, 7 α

толық емес бекiткiш рамамен бекiтiлген штрек тəрiздi қазба үшiн,

k = 0, 810 + 28, 7 α

мұнда, α - үйкелiс коэффициентi.

Сыртқы күш ауаның алғашқы энергиясын азайтуы (үйкелiс күшi) немесе оны жоғарылатуы (мысалы, желдеткiштiң жұмыс кезiн де) мүмкiн. Бiрiншi жағдайда. h > 0 ,

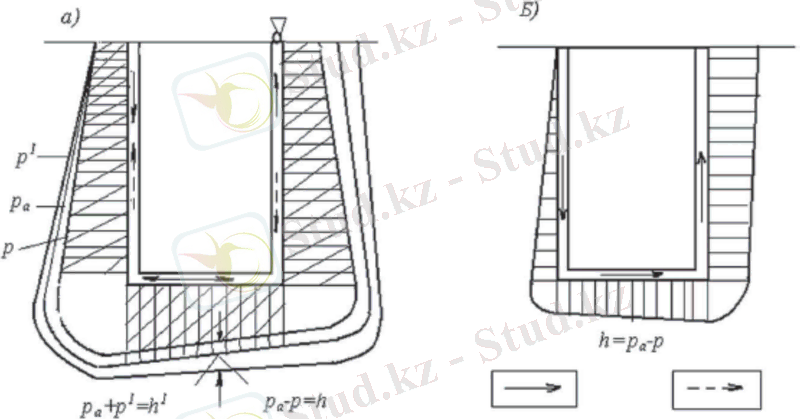
6. 4-сурет . Абсолютті қысымның ( а ) эпюрасы мен депрессиясы ( б ) : pаатмосфералық қысым; р’ - желдетудiң сору кезiндегi қысымы; p’’ - бұл да сол, айдау кезiнде; 1 - сорып желдету кезiндегi ауа қозғалысы; 2 -айдау кезiндегi ауа қозғалысы.

Ал екiншi жағдайда h < 0 ; (6. 15) теңдеуiндегi жақшадағы екi қосылғыш ағынның потенциалды энергиясының өзгеруiн, ал үшiншiсi - оның кинетикалық энергия өзгерiсiн көрсетедi. Сонымен, ағынның кез келген екi қимасы арасындағы толық энергия өзгерiсi осы учаскеде ауа қозғлысының кедергiсiн жеңуге шығындалатын (h > 0) энергияға немесе ағынға түсетiн энергияға (h < 0) немесе екеуiн де бiр мезгiлде тең болады.

(6. 15) теңдеуiндегi төмендегiден көрiнетiндей ауа қысымы, тереңдiктегi атмосфералық қысым болып табылмайды. Жеңiлiрек болу үшiн Р1 = Р2 = Р деп алсақ (6. 15) теңдеуi мына түрге енеді:

(p1 - p2) +g(ρ1z1 - ρ2z2) + [ k1(ρ1u /2) - k2(ρ1u /2) ] =

= p1 + gρΔz - p2 + ΔPдин= pa - p2 + Δpдин = h (6. 16)

мұнда, pa - z2 тереңдiктегi атмосфералық қысымға тең болатын қысым. (6. 16) теңдеуінен шығады,

р2 = pa - (h - Δpдин)

Осылайша р2 қысымы z2 тереңдіктегі атмосфералық қысымға тең жəне ол, I - II қима арасындағы қозғалған ауаның жоғалтқан энергиясы мен осы қима арасындағы динамикалық қысым айырмасына тең болатындай шамаға кемидi (6. 4-сурет) .

Бернулли теңдеуiнен h=const кезiнде қимадағы ауаның қозғалыс жылдамдығының өзгеруi қысымның өзгеруiне əкеледi. Сондықтан қимадағы ауа қозғалысының жылдамдығының артуы (мысалы, оның шығындауы арқылы кемуi) оның статикалық қысымын кемiтедi не керiсiнше. Бернулли теңдеуi шахталық аэродинамиканың негiзгi теңдеулерiнiң бiрi. Өйткенi ол аэродинамикалық мəселелерді бiрiктiрiп, оның көптеген сұрақтарына жауап бередi. Ол ауа ағынының көлем бiрлiгiндегi кинетикалық жəне потенциалық энергияның балансын өрнектейдi. p1 p2 қысымдар айырмасы желдеткiштiң салдарынан болады да, ол желдеткiштiң депрессиясы hв деп аталады.

Қосымша қысымдар айырмасы gp1 z1 - p2 z2 табиғи фактордан пайда

Болатындықтан сорудың табиғи депрессиясы деп аталады. ΔPдин - дi hдин -мен белгiлейiк. Сонда (6. 15) теңдеуi мына түрге енедi:

hв ± he ± hдин = h (6. 17)

(6. 17) теңдеуiндегi he ± hдин өрнегi, желдеткiштен алынатын I жəне II қима арасындағы толық энергия ағынының өзгерiсi болып табылады: Яғни:

hпол ± he = h (6. 18)

Табиғи сорылу энергия ағыны (he > 0) болғанда ұлғайта алады, (he < 0) болғанда кедергi рөлiн атқарады. Ағынға əсер етудiң осындай факторлары басқаша да болуы мүмкiн, (гидрошахтадағы көпіршіктердің ашық ағыны, сағадан соғатын жел жəне т. б. )

Бернулли теңдеуiн бiрнеше энергия көзiне, барлық кедергi түрiне қолдануды қорыта отырып, табамыз:

hвн = h (6. 19)

мұнда, hвн - сыртқы көзден түсетiн ауаның көлем бiрлiгiнiң энергиясы; h - көлем бiрлiгiнiң оның қозғалысына келтiретiн кедергiнi жеңуге шығындалатын энергиясы.

(6. 19) теңдеуiнен көрiнгендей қазбадағы сыртқы көзден түсетiн ауа ағынының адиабатты жағдайдағы ауа қозғалысына ауа қозғалысы жолындағы энергия толықтай барлық кедергiлердi жеңуге шығындалады.

Жергiлiктi кедергiні есептеу .

Жергiлiктi кедергiнiң депрессиясын есептеудi анықтаушы күштiң тепе-теңдiгi (7. 8) формуласынан шығарып алуға болар едi. Бiрақ оны қолдану ауа қозғалысын нақты ең үлкен жылдамдығын анықтау қажеттiлiгiнен қиындайды. Бұл мақсат үшiн тəжiрибемен табылған формуланы пайдаланады. Мұның мəнi жергiлiктi кедергiнiң депрессиясы ағын энергиясының бөлiгi болатындығында. Яғни:

h= ξρu2/2 (7. 19)

мұнда, ξ - жергiлiктi кедергi коэффициентi.

Ауа жылдамдығын оның шығынымен өрнектеп табамыз.

h = ξ(ρ/2S2) Q2 = RQ2 (7. 20)

мұнда, S - қазбаны көлденең қимасының ауданы, м2; Q - ауа шығыны, м3/сек; R - Hc2/м8 қазба учаскесiнiң жергiлiктi кедергiсiмен қоса алғандағы аэродинамикалық кедергiсi, ол келесі формуламен анықталады:

R = ξρ/2/S2 (7. 21)

(7. 19) өрнегiнен қазбаның жалпы депрессиясындағы жергiлiктi кедергiнiң депрессиясы ауа жылдамдығы үлкен болған сайын арта түсетіні байқалады. Ауа жылдамдығының ең үлкен жерде (желдеткiш арналарында, оқпан сағасы маңында т. б. ) жергiлiктi кедергiнің депрессиясы бiрнеше жүздеген паскалға жетуi мүмкiн. Жергiлiктi кедергiлерден тұратын күрделi қатардың (желдеткiштер арнасы, крос синги жəне басқалар) жалпы депрессия қатардағы жергiлiктi кедергiлердiң депрессиясымен (17. 9) формуласымен анықталатын үйкелiс депрессиясының қосындысына тең.

Желдетіс терезесiндегi қысымның (Па) жоғалуын анықтау үшiн А. А. Харев келесі формуланы ұсынады:

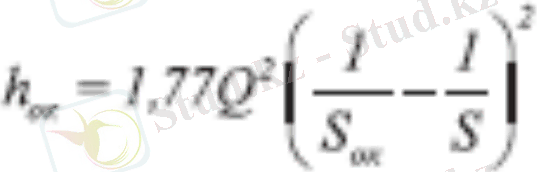(7. 22)

мұнда, Q - терезеден өтетiн ауа шығыны, м3/сек; Soк - терезе ауданы, м2; S - қазбаның терезе орнатылған жердегi көлденең қимасының ауданы, м2. (7. 22) формуласы Soк/S кез келген мəнiне тура келеді.

Жергiлiктi кедергi коэффициентiн анықтау .

Əдетте жергiлiктi кедергi коэффициентi ξ эксперименттiк жолмен анықталады. Ол үшiн жергiлiктi кедергi учаскесiнiң депрессиясын, жергiлiктi кедергiге дейiнгi жəне онан кейiнгi ауа қозғалысы жылдамдығын жəне ауаның тығыздығын анықтайды. Сонан соң (7. 19) формуласы бойынша ξ мəнiн есептейдi. Табылған ξ мəнi осыған есептелген жылдамдықпен үйлесуi керек. ξ мəнi жергiлiктi кедергiнiң түрi мен қазбаның бұдырлық дəрежесiне тəуелдi. Қазба жағдайында ξ мəнi Re санына тəуелсiз. Дегенмен, жалпы жағдайда ξ (Re) тəуелдiлiгi α(Re) тəуелдiлiгiне ұқсас. ξ коэффициентiне ағынның қатты шекарасындағы жеке элементтердiң салыстырмалы көлемi мен формасы əсер етедi. Сондай-ақ, ауа ағынының шұғыл ұлғаюында ξ коэффициентi қазбаның өзгерiс болғанға дейiнгi жəне онан кейiнгi көлденең қимасының қатынасы үлкен болған сайын үлкен болады.

Егер қиманың бiрiншiсiнен екiншiсiне өтуi неғұрлым бiркелкi болса, онда ξ коэффициентi азаяды. Ағынның бұрылу бұрышы үлкен болған сайын, ξ мəнi артады, ал бұрыш жиегi доғалданған сайын кемидi. ξ мəнi ауа қозғалысына қарсы орналасқан қуыспен тiк бұрыш жасағанда айтарлықтай ұлғаяды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.