Үзіліссіз кездейсоқ шамалардың үлестірім функциясы мен сандық сипаттамалары


КІРІСПЕ2
1. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ ҮЛЕСТІРІМ ФУНКЦИЯСЫ3
2. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫ5
ҚОРЫТЫНДЫ6
Пайдаланылған әдебиеттер тізімі7
КІРІСПЕБұл реферат жұмысының тақырыбы: “Үзіліссіз кездейсоқ шаманың сандық сипаттамалары” деп аталады.
Жұмыстың құрлымы: кіріспеден, 1 тараудан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады. Әр бөлімде егжей-тегжейлі ақпарат берілген және теңдеулер жүйесі туралы қарастырылған . Осы тақырыптарды зерттей отырып, сызықтық оператордың векторлық мәні, қолданулары туралы ақпараттар берілген.
Жазылып отырған реферат жұмысында бұл мектеп математика курсында математиканы оқып-үйренуге айтарлықтай орын беріледі. Сонымен қатар қазіргі қолданылып жүрген оқу бағдарламасы мектепте оқылатын дәстүрлі математикалық білім мазмұнына да, оны оқыту жүйесіне де үлкен өзгерістер енгізгендігі жайында айтылады. Балалардың математикаға деген ынтасын арттыруға, олардың өз бетінше жұмыс істей білу дағдысын тәрбиелеуге ерекше назар аударылады. Математикалық есеп оқушылардың ұғымдарды, теорияны және математика әдістерін меңгерудің тиімді де, айырбасталмайтын құралы болып табылады. Оқушылардың ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктері мен дағдыларының қалыптасуында, практикамен байланысын көрсетуде есептің алатын орны өте зор екендігі көрсетіледі. Математиканы оқытудағы басты мақсаттарға жетуге есеп - басты қызметші болып табылады.
1. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ ҮЛЕСТІРІМ ФУНКЦИЯСЫХ кездейсоқ шама дискретті болса оның үлестірім заңы кесте түрінде жазылады. Ал үзіліссіз кездейсоқ шаманың қабылдайтын мәндері шексіз болғандықтан ондай үлестірім заң жазылмайды. Сондықтан үлестірім функциясы ұғымын енгіземіз.
Анықтама . Х кездейсоқ шаманың х нақты саннан кіші мән қабылдау ықтималдығын кездейсоқ шаманың үлестірім функциясы деп атайды және Ғ(х) деп белгілейді:
F(х) = Р (Х < x) .
Кейде үлестірім функциясын «интегралдық функция» деп те атайды.
Үлестірім функциясының қасиеттері:
1-қасиет
.
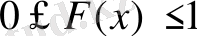 (анықтама бойынша үлестірім функциясы ықтималдық болып табылады) .
(анықтама бойынша үлестірім функциясы ықтималдық болып табылады) .
2-қасиет
. Үлестірім функциясы кемімейтін функция, яғни
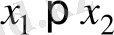 болса
болса
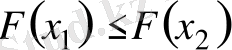 (
(
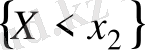 оқиғасы
оқиғасы
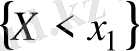 оқиғасын қамтиды) .
оқиғасын қамтиды) .
3-қасиет
.
 (
(
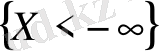 оқиғасы жалған оқиға болғандықтан
оқиғасы жалған оқиға болғандықтан
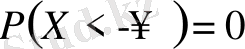 ,
,
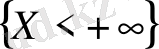 оқиғасы ақиқат оқиға болғандықтан
оқиғасы ақиқат оқиға болғандықтан
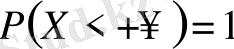 ) .
) .
4-қасиет
.
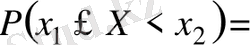
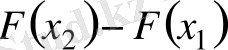 .
.
Анықтама. Кездейсоқ шаманың үлестірім функциясынан алынған туынды кездейсоқ шаманың үлестірім тығыздығы деп аталады және f(x) деп белгіленеді:
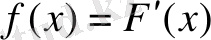
Кейде үлестірім тығыздығын «дифференциалдық функция» деп те атайды. Дифференциалдық функция Х кездейсоқ шаманың мәндері тәжірибені қайталап жасағанда х нақты санының маңайында қаншалықты жиі пайда болатындығын көрсетеді.
Дифференциалдық функция белгілі болғанда кездейсоқ шаманың үлестірім функциясын табу қиын емес:
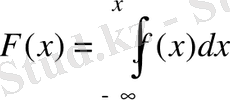 .
.
Дифференциалдық функция қасиеттері:
1-қасиет
.
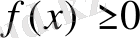 (кемімейтін функция туындысы теріс болмайды) .
(кемімейтін функция туындысы теріс болмайды) .
2-қасиет
.
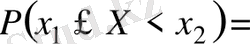
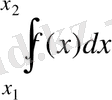 , себебі,
, себебі,
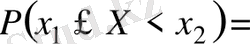
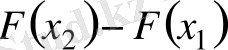
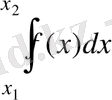 .
.
3-қасиет
.
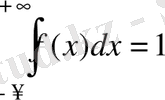 .
.
Мысал . Х кездейсоқ шама үлестірім тығыздығымен берілген
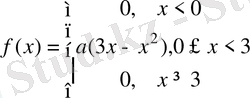 .
.
Табу керек: 1) белгісіз
а
-ны; 2)
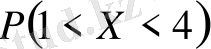 ; 3) Интегралдық функцияны; 4) Дифференциалдық және интегралдық функция графиктерін салу.
; 3) Интегралдық функцияны; 4) Дифференциалдық және интегралдық функция графиктерін салу.
Шешуі
. 1) Дифференциалдық функцияның қасиеті бойынша
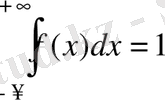 . Біздің жағдайымызда тығыздық үш интервалда және әр интервалда тығыздық түрлі формулалармен берілген, сондықтан:
. Біздің жағдайымызда тығыздық үш интервалда және әр интервалда тығыздық түрлі формулалармен берілген, сондықтан:
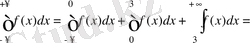
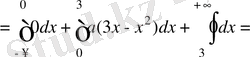
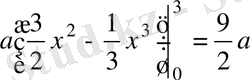 .
.
Сонда,
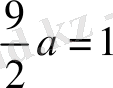 осыдан
осыдан

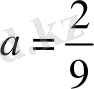 .
.
2)
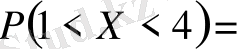
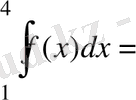
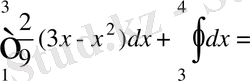
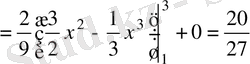 .
.
3) Интегралдық функцияны табайық.
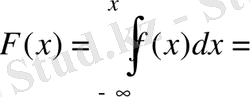
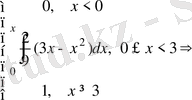
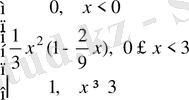 .
.
4) Дифференциалдық және интегралдық функция графиктері суретте көрсетілген.
2. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫАнықтама. Үзіліссіз кездейсоқ шаманың математикалық үміті деп оның х мәні мен үлестірім тығыздығы көбейтіндісінен алынған анықталған интегралы айтады
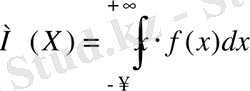 .
.
Мұндағы меншіксіз интегралды жинақталады деп қарастырамыз (егер жинақталмаса кездейсоқ шаманың математикалық үміті жоқ болады) .
Егер үзіліссіз кездейсоқ шаманың М(х) математикалық үміті бар болып, оның f(x) үлестірім тығыздығы жұп функция болса, онда
М(х) = 0
болады. Жалпы, егер кездейсоқ шаманың f(x) үлестірім тығыздығы қандай да бір х=а нүктесіне қарағанда симметриялы болса, онда
М(х) = а
болады.
Анықтама . Үзіліссіз кездейсоқ шаманың дисперсиясы деп оның х мәнінің математикалық үміттен ауытқуының квадраты мен үлестірім тығыздығы көбейтіндісінен алынған анықталған интегралы айтады
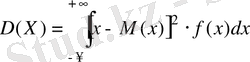 .
.
Әдетте дисперсия оңай есептелiнетiн мынадай формула қолданылады:
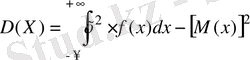
Үзіліссіз кездейсоқ шама дисперсиясынан алынған квадрат түбiр орта квадраттық ауытқу болады:
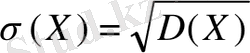 .
.
Осы реферат жұмыста “ Үзіліссіз кездейсоқ шаманың сандық сипаттамалары ” туралы біліп, білімімізді кеңейтіп, математикалық ой-өрісімді кеңейттік.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz