Кездейсоқ шамалар: үзіліссіз шаманың үлестірім функциясы, үлестірім тығыздығы және математикалық үміті


ЖОСПАР
1. КЕЗДЕЙСОҚ ШАМАЛАР
2. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ ҮЛЕСТІРІМ ФУНКЦИЯСЫ
3. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫ
Пайдаланылған әдебиеттер тізімі
1. КЕЗДЕЙСОҚ ШАМАЛАР
Бiз, кездейсоқ оқиға түрлерiмен (үйлесiмсiз және үйлесiмдi оқиғалар, тәуелдi және тәуелсiз оқиғалар) танысып, олардың ықтималдықтары қандай деген мәселемен айналыстық. Бiр сөзбен айтар болсақ, тәжiрибе нәтижесiнде пайда болатын оқиғаның сапалық сипаттамасы - кездейсоқ оқиғамен - жұмыс жасадық.
Ендi бiз оқиғалардың сандық сипаттамасымен танысамыз. Сандық болғандықтан оқиға қандай да бiр сандық шамалармен сипатталуы керек. Мысалы, бiр күннiң сандық сипаттамасы ретiнде оның ұзақтығын алуға болады. Бiр күнде 24 сағат бар. Ол өзгермейдi, яғни тұрақты шама. Ал осы бiр күн iшiнде адамның жұмыс iстеу уақытын алатын болсақ, ол өзгередi, яғни кездейсоқ шама болады. Адам бiр күнде 7-8 сағат, 3-4 сағат, тiптен мүлде жұмыс iстемеуi де мүмкiн.
1. 1. Кездейсоқ шама. Бiрнеше мысал қарастырудан бастайық.
1-мысал . Теңгенi үш рет лақтырғанда елтаңба жағымен түсу санын қарастырайық.
Жасалатын тәжiрибе: теңгенi үш рет лақтыру.
Iзделiндi шама: осы үш ретте елтаңба жағымен түсу саны. Теңгенi үш рет лақтырғанда бiрде-бiр рет елтаңба жағымен түспеуi мүмкiн, немесе 1, 2 рет не тiптi 3 ретте де елтаңба жағымен түсуi мүмкiн. Тәжiрибе алдында iзделiндi шама өзiнiң мүмкiн 4 мәнiнiң қайсысын қабылдайтыны белгiсiз, тек мiндеттi түрде осы төрт мәннiң бiреуiне тең болады.
2-мысал . Қандай да бiр қалада бiр айда дүниеге келген сәбилер санын қарастырайық.
Жүргiзiлетiн бақылау: Бiр айда дүниеге келген сәбилердi бақылау.
Iзделiндi шама: Осы дүниеге келген сәбилер саны. Ол қалада бiр айда дүниеге бiрде-бiр сәби дүниеге келмеуi мүмкiн, немесе бiреу, екеу, т. с. с. сәбилер дүниеге келуi мүмкiн. Тәжiрибе алдында iзделiндi шама өзiнiң мүмкiн мәндерiнiң (0, 1, 2, . . . ) қайсысын қабылдайтыны белгiсiз, тек мiндеттi түрде осы мәндердiң бiреуiне ғана тең болады.
3-мысал . Мерген центрi белгiленген, радиусы R-ге тең нысананы көздеп атты дейiк. Тиген оқтың центрден қаншалықты ауытқығанын табайық.
Жүргiзiлген сынақ: мергеннiң нысананы көздеуi.
Iзделiндi шама: оқтың центрден қаншалықты ауытқығаны. Мерген дәл центрге тигiзуi мүмкiн, ол кезде ауытқу нөлге тең. Ал егер центрден өзге жерге тисе, сол жерден бастап центрге дейiнгi ара-қашықтықты керектi дәлдiкке дейiн әруақытта өлшеп алуға болады. Сонда iзделiндi шама 0 мен R-дiң арасында жатқан кез келген санды қабылдай алады. Тәжiрибе алдында iзделiндi шама өзiнiң мүмкiн мәндерiнiң ([0, R] кесiндiсiне тиiстi кез келген сан) қайсысын қабылдайтыны белгiсiз, тек мiндеттi түрде осы мәндердiң бiреуiне ғана тең болады.
Анықтама . Тәжiрибе нәтижесiнде алдын-ала белгiсiз, бiрақ нақтылы бiр мән ғана қабылдайтын шаманы кездейсоқ шама деймiз.
Кездейсоқ шамаларды латын алфабитiнiң үлкен әрiптерiмен (Х, У, Z), ал олардың қабылдайтын мүмкiн мәндерiн кiшi әрiптерiмен (х 1 , х 2 , . . . , х п , у 1 , у 2 , . . . , z 1 , z 2 , . . . ) белгiлейдi.
Қарастырған мысалдардағы шамамалардың бәрi де кездейсоқ шамалар екен: Х - теңгенi үш рет лақтырғанда елтаңба жағымен түсу саны; У - бiр айда дүниеге келген сәбилер саны; Z - оқтың центрден ауытқу саны.
Бастапқы екi мысалда, бiз кездейсоқ шаманың қабылдайтын мәндерiн нақтылы санай аламыз. 1-мысалда ол мәндер: 0 (бiре-бiр рет елтаңба жағымен түспедi), 1 (елтаңба жағымен 1 рет түстi), 2 (елтаңба жағымен 2 рет түстi), 3 (елтаңба жағымен 3 рет түстi) .
Ал 2-мысалда, ол мәндер: 0 (бiрде-бiр сәби дүниеге келмедi), 1 (бiр сәби дүниеге келдi), 2 (екi сәби дүниеге келдi), т. с. с.
2. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАНЫҢ ҮЛЕСТІРІМ ФУНКЦИЯСЫ
Х кездейсоқ шама дискретті болса оның үлестірім заңы кесте түрінде жазылады. Ал үзіліссіз кездейсоқ шаманың қабылдайтын мәндері шексіз болғандықтан ондай үлестірім заң жазылмайды. Сондықтан үлестірім функциясы ұғымын енгіземіз.
Анықтама . Х кездейсоқ шаманың х нақты саннан кіші мән қабылдау ықтималдығын кездейсоқ шаманың үлестірім функциясы деп атайды және Ғ(х) деп белгілейді:
F(х) = Р (Х < x) .
Кейде үлестірім функциясын «интегралдық функция» деп те атайды.
Үлестірім функциясының қасиеттері:
1-қасиет
.
 (анықтама бойынша үлестірім функциясы ықтималдық болып табылады) .
(анықтама бойынша үлестірім функциясы ықтималдық болып табылады) .
2-қасиет
. Үлестірім функциясы кемімейтін функция, яғни
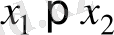 болса
болса
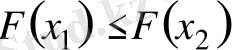 (
(
 оқиғасы
оқиғасы
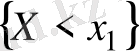 оқиғасын қамтиды) .
оқиғасын қамтиды) .
3-қасиет
.
 (
(
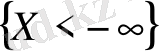 оқиғасы жалған оқиға болғандықтан
оқиғасы жалған оқиға болғандықтан
 ,
,
 оқиғасы ақиқат оқиға болғандықтан
оқиғасы ақиқат оқиға болғандықтан
 ) .
) .
4-қасиет
.

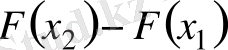 .
.
Анықтама. Кездейсоқ шаманың үлестірім функциясынан алынған туынды кездейсоқ шаманың үлестірім тығыздығы деп аталады және f(x) деп белгіленеді:

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz