Ықтималдықты есептеуде комбинаторика элементтерін қолдану


КІРІСПЕ2
1. Ықтималдықты есептеуде комбинаторика элементтерін қолдану3
2 Қосу ережесі6
3 Көбейту ережесі7
Қорытынды9
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР10
Комбинаторика (лат. Combino - жалғастырамын) - комбинаторикалық анализ деп те аталады.
Комбинаторикалық анализ комбинаторикалық математика, комбинаторика - математиканың кез келген шектеулі жиын (шектеудің кейбір шарттарын шексіз жиын) бөліктерінің орналастырылуы мен өзара орналасуына байланысты мәселелерін зерттейтін бөлімі.
Комбинаторикалық сипаттағы идеялар ықтималдық теориясы, алгебра тәрізді математикалық бөлімдерінде өте кең тараған. Комбинаторикалық анализ есептері ерте кезден - ақ белгілі болған. Оның дамуына көптеген математиктер елеулі үлес қосты. Бірақ комбинаторикалық анализ өз алдына пән ретінде тек 20 ғасырда ғана қалыптаса бастады. Комбиторикалық графтар теориясы, шектеулі автоматтар теориясы тәрізді математиканың салаларымен тығыз байланысты. Оның тәжірибелері ғылыми тәжірибелерді жоспарлауды және оларға талдау жасауда, сызықтық және динамикалық бағдарламалауда, математикалық экономикада, т. б. ғылым мен техникалық көптеген салаларында қолданылады. Комбинаторикалық анализ проблемасының үш түрі бар.
Санап шығу есептерінде объектілердің шектеулі жиынынды кездесетін шарттарды қанағаттандыратын орналастырулар саны қарастырады. Іс жүзінде мұндай есептер жасаушы функциялар әдісі мен Д. Пойаның (1887-1985) (американдық математик) санап шығу әдісінің көмегімен шешіледі.
Салу есептерінде кейбір қасиеттері сақталатын шектеулі жиын бөліктері конфигурациясының болуы, егер болса оның салынатындығы туралы мәселелер қарастырылады. Таңдап алу есептерінде ішкі жиын бөліктерінің кейбір құрамын таңдап алу шарттары зерттеледі. мұндай есептерді шешкенде комбинаторлық ойлармен қатар алгебралық аппарат та қолданылады.
Дискреттік математика - математиканың дискретті құрылымдардың қасиеттернін зерттейтін саласы. Мұндай құрылымдарға шектеулі топтар, шектеулі графтар, сондай-ақ, ақпаратты түрлендіргіш кейбір математикалық модельдер шектеулі автоматтар, Тьюринг машинасы, т. б. жатады. Бұлар шектеулі сипаты бар құрылымдар болып есептеледі. Дискретті математиканың шектеулі құрылымдарды зерттейтін бөлігін шектеулі математика деп атайды. Дискреттік математикада, жоғарыда аталған шектеулі құрылымдармен бірге, кейбір алгебралық жүйелер, шексіз графтар, белгілі бір түрлері есептеу сұлбалары, т. б. зерттеледі. «Дискреттік математика» және «шектеулі математика» ұғымдарының синонимі ретінде кейде «дискреттік талдау» термині қолданылады.
Ықтималдықтар теориясы мен математикалық статистиканы оқып үйренуге өмірдің өзі негіздейді. Өмірдің өзі кездейсоқ жағдайларға толы. Әр адам сол кездейсоқтыққа дайын болу үшін мәліметтерді талдаудың негізгі әдістерін, ықтималдық заңдылықтарын білуі қажет. Ықтималдықтар теориясы және математикалық статистика әдістері алуан түрлі салаларда кеңінен қолданылады, оның ішінде физика, геодезия, астрономия, атқылау теориясы, психология, лингвистика, биология, медицина, социология, археология және адамның басқа да қызмет салаларында пайдаланылады. Сол себепті, мектеп математикасында ықтималдықтар теориясы мен математикалық статистика элементтері оқытыла бастады. Математиканың бұл саласы оқушының логикалық ойлау қабілетін дамытуға, шыңдауға бағытталған.
Кездейсоқ оқиғаның ықтималдығын есептеу үшін біз комбинаторика элементтерін пайдаланымыз. Комбинаторика әдістері барлық мүмкін болатын жағдайлар санын есептеуге септігін тигізеді. Комбинаторикалық есептердің шешулерінің санын есептеу үшін түрліше формулалар қолданылады, олар негізінен қосу және көбейту ережелеріне сүйенеді.
Қосу ережесі
Егер А элементті m тәсілмен, ал В элементті n тәсілмен таңдап алатын болса және А мен В элементтерін таңдау бір-бірінен өзгеше болған жағжайда, «А немесе В»-ны таңдау жолы (m+n) тәсілмен орындалады.
1-есеп. «Халық» банкінде 3 сарапшы, 5 программист және 10 мененджер жұмыс істейді. Мереке күніне байланысты бір қызметкерді кезекшілікке қою керек. Мекеме бастығы кезекшіні неше тәсілмен таңдай алады?
Шығарылуы.
Мекеме бастығы бір сарапшыны
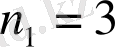 тәсілмен, бір программистті
тәсілмен, бір программистті
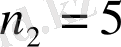 тәсілмен, бір мененджерді
тәсілмен, бір мененджерді
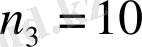 тәсілмен таңдай алады. Мекеме бастығы бір қызметкерді қосу ережесі бойынша
тәсілмен таңдай алады. Мекеме бастығы бір қызметкерді қосу ережесі бойынша
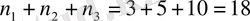 тәсілмен таңдай алады.
тәсілмен таңдай алады.
Көбейту ережесі
Егер х элементін k тәсілмен, ал у элементін m тәсілмен таңдауға болса,, онда
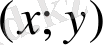 жұбын
жұбын
 тәсілмен таңдап алуға болады.
тәсілмен таңдап алуға болады.
2-есеп. Жанат пен Марат бір-бірімен ренжісіп қалғандықтан, екеуі бір автобусқа отырғысы келмейді. Жатақханадан университетке дейін сағат 7-ден 8-ге дейін 7 автобус жүреді. Соңғы автобусқа үлгермей қалса, онда дәріске кешігеді. Жанат пен Мараттың дәріске кешікпей, университетке әртүрлі автобуста келулерінің неше тәсілі бар?
Шығарылуы.
Жанат университетке
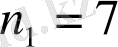 (7 автобустың біреуімен) әртүрлі тәсілмен келе алады, ал Марат университетке
(7 автобустың біреуімен) әртүрлі тәсілмен келе алады, ал Марат университетке
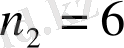 тәсілмен (себебі, бір автобуста Жанат отыр) жете алады. Олай болса, көбейту ережесі бойынша Жанат пен Марат дәріске кешікпей, университетке
тәсілмен (себебі, бір автобуста Жанат отыр) жете алады. Олай болса, көбейту ережесі бойынша Жанат пен Марат дәріске кешікпей, университетке
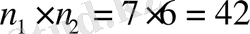 тәсілмен жете алады.
тәсілмен жете алады.
Алмастырулар
. Алмастырулар
деп бір-бірінен айырмашылығы тек қана орналасу ретінде ғана болатын
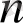 элементтің
элементтің
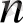 элементінен жасалған реттелген ішкі жиындарды айтамыз және алмастырулар санын келесі формуламен есептейміз:
элементінен жасалған реттелген ішкі жиындарды айтамыз және алмастырулар санын келесі формуламен есептейміз:
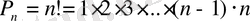
3-есеп. Бірдей карточкаларда А, К, П, Т, І әріптері жазылған. Карточкаларды әбден араластырып, бір қатарға қойғанда КІТАП сөзінің шығу ықтималдығы қандай?
Шығарылуы . Бес карточканың бір қатарға өзара орналасуының бір-бірінен айырмашылығы тек орналасу ретінде ғана болғандықтан (ТПАКІ, КТПАІ, ПТАІК, КІТАП, . . ), барлық мүмкін жағдайлар санын алмастыру формуласы бойынша табамыз, яғни
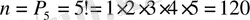 .
.
КІТАП сөзі тек бір жағдайда ғана пайда болады. Олай болса, ықтималдықтың классикалық анықтамасы бойынша, КІТАП сөзінің шығу ықтималдығы
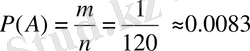
Орналастырулар.
Орналастырулар деп бір-бірінен айырмашылығы орналасу ретінде немесе құрамында болатын
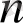 элементтің
элементтің
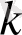 элементінен жасалған реттелген ішкі жиындарды айтамыз және орналастырулар санын келесі формуламен есептейміз:
элементінен жасалған реттелген ішкі жиындарды айтамыз және орналастырулар санын келесі формуламен есептейміз:
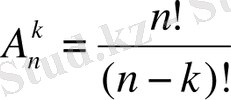
4-есеп. Ш, К, М, Н, Т, Ы, Е әріптері жазылған бірдей 7 карточка ішінен 4 карточка алып, бір қатарға қойылған. Сонда КЕНТ сөзінің шығу ықтималдығы қандай?
Шығарылуы. 7 әріптен алынған әрқайсысы 4 әріптен құралған реттелген ішкі жиындардың бір-бірінен айырмашылығы немесе ретінде, немесе құрамында болады (ШМТН, КНЕШ, ШНКЕ, . . . ) . Олай болса, орналастырулар формуласы бойынша барлық мүмкін жағдайлар саны
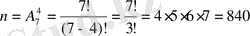 -қа тең.
-қа тең.
Ал, КЕНТ сөзі үшін қолайлы жағдайлар саны 1. Ендеше, ізделінді ықтималдық
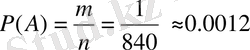 .
.
Терулер
. Терулер деп бір-бірінен айырмашылығы тек құрамында ғана болатын
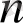 элементтің
элементтің
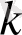 элементінен жасалған реттелген ішкі жиындарын айтамыз және терулер санын келесі формуламен есептейміз:
элементінен жасалған реттелген ішкі жиындарын айтамыз және терулер санын келесі формуламен есептейміз:
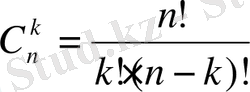
5-есеп. Лотореяның 1 тиражында 100 билет бар. Олардың 50-і ұтысты билеттер және 50-і ұтыссыз билеттер. Екі билет сатып алынған. Сатып алынған екі билеттің де ұтысты болу ықтималдығы неге тең?
Шығарылуы. Барлық мүмкін жағдайлар терулер формуласы бойынша
-ге тең.
Қолайлы оқиғалар саны
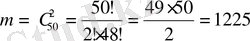 .
.
Олай болса, ізделінді ықтималдық
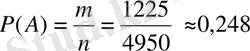 -ге тең.
-ге тең.
Өмірдегі сан мыңдаған оқиғаларға математикалық тұрғыда қортынды жасауға арналған негізгі тәсілдердің біреуі мүмкіндіктерді санау немесе комбинаторика болып табылады. Жиынның элементтерінің санын, оларды реттеу санын табу, барлық мүмкін болмыстардың санын табу қажеттігі өмірде көптеп кездеседі. Осы мәселені оңтайлы шешуге бізге мүмкіндік санау тәсілдері немесе комбинаторика көмектеседі. Математикалық оқиғаларды көбінесе жиындармен жиындарға қолданылатын амалдар арқылы белгілеп, мүмкіндіктер санын «қосу» және «көбейту» ережесін қолданып есептеу комбинаториканың негізі болады да комбинаторикалық мазмұнды есептерді шешу ісі көбінесе оны қандай бір жиынның элементтерінің санын, бұл элементтерді белгілі ретпен орналастыру мүмкіндігін немесе оның ішкі жиындарын санау арқылы шығарылатын болады.
Төменде комбинаторикалық бағыттағы әртүрлі есептерге мысалдар келтірілген. Бұл есептерді өз бетіңмен шығар.
1. а) Суретте неше кесінді кескінделген?
б) Суретте кескінделген үшбұрыштар санын тап.
2. 2 тиынды тастағанда әр түрлі неше тәсілмен түсуге болады?
3. 0; 1; 2; 3; 4; цифрлары арқылы қанша үш таңбалы сан жазуға болады? Бұлардың нешеуі 5 -ке бөлінеді? а) Цифр қайталанбайды. б) Цифр қайталанады.
4. 5х5 шахмет тақтасының сол жақ астыңғы көзіндегі бала жоғары немесе оң бағытқа бір аттап көшу арқылы оң жақ жоғарғы көзге неше әр түрлі маршрутпен жетуге болады?
5. Әр кесіндіде 4 нүкте болатындай етіп 10 нүкте және 5 кесіндіні орналастыр.
6. Дүние жүзіндегі барлық адамдардың ішінен таныстарының саны тақ адамдардың жұп болатынын дәлелде.
Енді комбинаторикалық есептерді шешудің негізгі тәсілдеріне тоқталсақ:
2 Қосу ережесіДербес жағдайдағы мүмкіндіктер санын есептеп, немесе ішкі жиынның элементтері мен оларды орналастыру сандарын есептеп өзара қосу және тізбе түрінде жазып өсу заңдылығын табу тәсілдері қолданылады. Бұл тәсілге жиындарға қолданылатын амалды пайдалансақ жиындардың бірігуінің элементерінің санын табуға арналған формуласын пайдаланамыз. Ал тізбекті пайдалансақ өзгеру заңдылығын, рекуренттік қатынасты байқау деген сияқты тәсілдер таңдауға тура келеді.
Мысал-1: 1-ден 100-ге дейінгі натурал сандардың ішінде 2 мен 3-тің кемінде біреуіне бөлінетін сан нешеу?
Шешуі: деп алсақ, 2 мен 3-тің кемінде біреуіне бөлінетін сандардың саны = 50 + 33 - 16 - ге тең болады. Мұндағы -2 мен 3-ке қатар бөлінетін сандар.
Мысал-2: 10 тор көзді жолақтың сол жақ шеткі көзіндегі тас оңға қарай 1 не 2 аттап көшу арқылы оң жақ шеткі көзге неше әр түрлі маршрутпен жетуге болады?
Шешуі: 2-ші көзге 1, 3-ші көзге 2 тәсілмен келе алады да 3- көзден бастап әр көзге оның алдындағы 2 көзден 1 не 2 аттап түсе алады. k-інші көзге келетін маршрут саны, рекурент формуласы бойынша есептеледі. Олай болса:,
Жауабы: 89- әр түрлі маршрут
Мысал -3: Сыныптағы 25 оқушының 15-і математика 9-ы физика пәнінен факультетив сабаққа қатысады да 6-ы бұл екеуінің қай-қайсысына қатыспайды. Екі факультетивке қатар қатысатын және тек математикаға қатысатын оқушылар қанша?
Шешуі: А- математикаға, В- физикаға қатысатын оқушылар жиыны болса =25 - 6 =19 болғандықтан екі фалультетивке қатар қатысатындар саны = 15 + 9 - 19=5 болады да тек математикаға ғана қатысатындар 15 - 5=10 оқушы.
Мысал-4: Алдындағы келтірілген 1 б) мысалдағы үшбұрыштар санын табайық.
Шешуі: Үшбұрыштың табанының сол жақ төбесі астыңғы табан бойындағы түйін нүктелерінде болатын үшбұрыштар санын оң жағынан бастап санап қоссақ, сәйкес 1, 2, 3, 4, 5, 6 болады да қосындысы 21-ді 2 еселеп алсақ суреттегі барлық үшбұрыштардың санын береді.
Жауабы: 42 үшбұрыш.
Мысал-5:
нүктелер тізбегінің санын квадрат сандар, ал төменгі
тізбектерді сәйкесінше үшбұрыш сандар және бестік сандар деп алайық.
а) 7- ші квадрат, үшбұрыш, бестік сандарды тап.
б) Квадрат, үшбұрыш, бестік сандарының заңдылығын тауып әр қайсысының 10- шы, 50- ші сандарын тап.
Шешуі: Квадрат сандардың заңдылығы айқын. Үштік сандар 2-сінен бастап алдыңғысына сәйкес 2, 3, 4, деген сияқты тізбектелген бүтін сандармен қосылып отыратындықтан 7-шісі 1+2+3+4+5+6+7=28 n-інші сан 1+2+ . . . + n = болады. Бестік сандар саны 1, 1+(1+3) = 2 + 3∙1, 5+(1+3+3) = 3+ (1+2) ∙3 . . .
яғни болады.
Мысал-6: А нүктесініен F-ке баратын әр түрлі неше маршрут бар?
Шешуі: В нүктесіне АВ және АDB 2 маршрутпен келуге болатындықтан B нүктесінің дәрежесі 2-ге, сол сияқты D-2, C-1, E-2 дәрежелі болады да F-ке маратын маршрут саны қосу ережесі бойынша 2+1+2=6 -ға тең болады.
3 Көбейту ережесіОқиға немесе жиынның әр элементінің мүмкігдігін есептеп барлық мүмкіндікті табу тәсілі көбейту ережесі арқылы жүзеге асырылады. Көбейту ережесін жиын арқылы анықтасақ n- элементтен тұратын А, m элементтен тұратын В жиындарының әр қайсысынан бір бір элемент алып құрастыруға болатын (а; в) парлар саны -ге тең. Осындай барлық мүмкін парлар жиынын А, В жиындарының Декараттық көбейтіндісі деп атап деп белгілейді.
Жоғарыдағы қортындыны қысқаша :
, болса деп жазамыз. Сол сияқты болатын k жиынның әр қайсы-сынан бір бір элемент алып құрастыруға болатын барлық k парлар саны - ға тең болады.
Мысал-1: 21 оқушысы бар сыныптың оқушыларын неше әр түрлі тәсілмен сапқа тұрғызуға болады?
Шешуі: 1- ші орынға 21- оқушының кез келгенін, 2- ші орынға 1- ші орынға тұрған оқушыдан басқа 20 оқушының кез келгенін, деген сияқты 21-інші орынға қалған 1 оқушыны таңдау арқылы 21- элементтен тұратын парлар таңдау керек болатындықтан сапқа тұрудың барлық мүмкіндігі . болады.
Мысал-2:
жиынтығынан солдан оңға қарай бағытпен «АСТАНА» сөзін әр түрлі неше тәсілмен оқуға болады?
Шешуі: С- әріптерінің әр қайсысына сол жақтағы А- дан баруға болатындықтан әр қайсысына 1, Т әрпінің әр қайсысына екі С- ның қайсысынан да баруға болатындықтан әр қайсысына 2 деген сияқты келуге болатын мүмкіндіктер бар болғандықтан барлық мүмкіндіктер саны Жауабы: Әртүрлі 36 тәсілмен оқылады.
Мысал-3: 6 лампа арқылы бөлмеге неше тәсілмен жарық беруге болады? (әр лампада жеке ажыратқыш бар, )
Шешуі: 6 лапаның әр қайсысында бөлмеге жарық беруге қатысудың «жану», «сөну» деген 2 мүмкіндігі болатындықтан есептің жауабы .
Коминаторика элементерін пайдаланып, ықтималдарды есептеу.
A = n(n-1) *(n-2) *(n-+1) ;
= n!:
C =
A, B, C,, , 32
A = n
, n2,, ,, n1=
C =
123\NAN
A =32 BAM
GGG
Мысал:Е, К, М, Н, Т, Ш, Ы.
1) 4-к;, , А һ 7*6*5*4*=840.
2) «КЕНТ» сөзінің шығу ықтималдығы.
P(A) = = = 0, 0012
n=840=A ; m= 1
Осы тәсілдермен қанша рет алмастыру жасауға болады.
«Шымкент» сөзінің шығу ықтималдығы.
P =7!=7*6*5*4*3*2*1=5040;
P(A) = = = 0, 0002
Мысал 2:
Анеферонс ойынында 32 карта ойнайды, 3 ойыншыға 10-10-нан таратылады. 2 картаны төнкеріп стол ортасынна кояды. .
- 2 тұз болуы;
- 1-еуі тұз, 1- еуі дама
n= C = = =496
m=C = = =6;
P(A) = = 12, 0012;
n=496
m=C *C = = = 1
P(B) = = 0, 032.
Қорытынды ... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz