Бірөлшемді кездейсоқ кезулер: баспалдақтық биіктіктер, Винер-Хопф факторизациясы және Фурье әдісі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:
Мазмұны
Кіріспе
Бұл жұмыста «баспалдақты» шамаларды жүйелі қолдану мен комбинаториялық тәсілдерге күш сала отырып, кездейсоқ кезудің есептері қарастырылады. Біз негізінен екі маңызды сұрақпен шектелеміз. Біріншіден, тиын лақтыруға қатысты қызықты нәтижелер жалпы жағдайға көшірілетіндігі және негізінен осы кезде дәл сондай тәсілдер қолданылатындығы көрсетілетін болады. Екінші сұрақ, бірінші уақытылы өту мен құлдыраудың есептерімен байланысты. Қазіргі кезде мұндай тақырыптарды белгілі Винер-Хопфтың теориясымен байланыстыру танымал болуда. Бірақ бұл байланыстар әдетте бейнеленгеніндей, бір- бірімен қатты тығыз емес. Бұл туралы (1. 3) тарауында талқыланатын болады.
Спарде-Андерсен ашқан флуктуация теориясындағы қуатты комбинаторлы тәсілдер барлық кездейсоқ кезулер теориясын жаңа қырынан көрсетті. Содан бері кездейсоқ кезулер мен кезектер теориясы арасында тығыз байланыстың кенеттен ашылуының қарқынды түрде дамуы ескерілді.
Дипломдық жұмыстың өзектілігі : Біздің жұмысымыздың тақырыбы бүкіл әлемде белсенді қарастырылып жатқан есептер мен өзекті мәселелердің бірі болып табылатын кездейсоқ кезу ұғымымен байланысты. Ықтималдық теориясы, физика, социология, медицина сонымен қатар популяциялық генетиканың көптеген мәселелері, шешімінде кездейсоқ кезулердің нақты типтерінің математикалық моделін құратын есептерге алып келеді. Біздің жұмысымыздың мәселелеріне елеулі еңбек сіңірген Д. Е. Бартон, Ф. Спицер, К. Ито, Г. Крамер, Б. В. Гнеденко және тағы басқа көптеген ғалымдардың есімдерін атап өтсек жеткілікті. Олай болса жұмысымыздың өзектілігі айқын.
Мақсаты: Көрсетілген процесстер моделінің қасиеттерін құру және зерттеу.
Міндеті: Кездейсоқ кезулердің нақты түрінің математикалық моделін құру.
Зерттеу нысаны: Кездейсоқ оқиғалар.
Зерттеу пәні : Сан түзуіндегі кездейсоқ кезу.
Идеал тиын лақтыру ойыны қазіргі күнде, өзінің көрнекілігімен көзге түсетін және жалпылау үшін жақсы ыңғайланған кездейсоқ кезудің көмегімен суреттеледі. Белгілі болғандай, егер
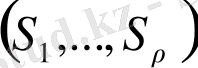 жолы
жолы
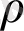 тиын лақтыру қатарының нәтижесі ретінде қарастырсақ, онда
тиын лақтыру қатарының нәтижесі ретінде қарастырсақ, онда
 дербес қосындылары пайда мәндерінің қатарын білдіреді. Геометриялық тұрғысынан қарастыру үшін, тиын лақтыру бірдей уақыт интервалынан соң орындалады деп болжау ыңғайлы, сондықтан
дербес қосындылары пайда мәндерінің қатарын білдіреді. Геометриялық тұрғысынан қарастыру үшін, тиын лақтыру бірдей уақыт интервалынан соң орындалады деп болжау ыңғайлы, сондықтан
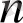 - ші тәжірибе
- ші тәжірибе
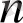 уақыт мезетінде жүзеге асады.
уақыт мезетінде жүзеге асады.
 тізбектелген дербес қосындылары
тізбектелген дербес қосындылары
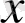 вертикальды осінің нүктелері арқылы өрнектелетін болады; олар кездейсоқ кезу жасайтын «бөлшектердің» күйі деп аталады. Бөлшек бірлік қадаммен түзу бойында жоғары немесе төмен қозғалатынын ескереміз. Жол осындай қозғалыстың графигін білдіреді.
вертикальды осінің нүктелері арқылы өрнектелетін болады; олар кездейсоқ кезу жасайтын «бөлшектердің» күйі деп аталады. Бөлшек бірлік қадаммен түзу бойында жоғары немесе төмен қозғалатынын ескереміз. Жол осындай қозғалыстың графигін білдіреді.
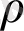 ұзындығының әрбір жолын кейбір кездейсоқ кезудің нәтижесі сияқты интерпритациялауға болады; осындай жолдардың
ұзындығының әрбір жолын кейбір кездейсоқ кезудің нәтижесі сияқты интерпритациялауға болады; осындай жолдардың
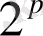 бар, және біз
бар, және біз
 ықтималдығын әрқайсысына тіркейміз. (Әрине, басқа да ықтималдың үлестірілімдері бар. Ол үшін қарастырып отырған кездейсоқ кезуді басқаларынан айыру үшін оны симметриялы деп атаймыз. )
ықтималдығын әрқайсысына тіркейміз. (Әрине, басқа да ықтималдың үлестірілімдері бар. Ол үшін қарастырып отырған кездейсоқ кезуді басқаларынан айыру үшін оны симметриялы деп атаймыз. )
Біз ондағы ықтималдық пен қарапайым оқиғалар кеңістігінің анықтамасын қорытамыз, бірақ олардың
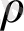 санынан тәуелділігі алаңдатады. Алдымен оның мәнін табу үшін, жолдың
санынан тәуелділігі алаңдатады. Алдымен оның мәнін табу үшін, жолдың
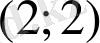 нүктесі арқылы өтетін оқиғасын қарастырамыз. Алғашқы екі қадамы оң болу қажет, және сондықтан осындай
нүктесі арқылы өтетін оқиғасын қарастырамыз. Алғашқы екі қадамы оң болу қажет, және сондықтан осындай
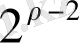 жолдары бар екені шығады. Күтілгендей, бұл оқиғаның ықтималдығы
жолдары бар екені шығады. Күтілгендей, бұл оқиғаның ықтималдығы
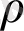 мәнінен тәуелсіз
мәнінен тәуелсіз
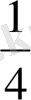 тең. Кез келген
тең. Кез келген
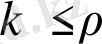 үшін жалпы жағдайда алғашқы
үшін жалпы жағдайда алғашқы
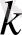 қадамы бекітілген күйімен
қадамы бекітілген күйімен
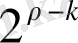 жолдары бар болады. Бұдан шығатыны, алғашқы
жолдары бар болады. Бұдан шығатыны, алғашқы
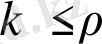 қадамдарымен анықталған оқиғалар
қадамдарымен анықталған оқиғалар
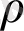 - дан тәуелсіз ықтималдыққа ие болатындығы шығады. Сондықтан практикада
- дан тәуелсіз ықтималдыққа ие болатындығы шығады. Сондықтан практикада
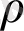 санының маңызы жоқ, егер ол жеткілікті үлкен болса. Басқаша айтқанда, кез келген
санының маңызы жоқ, егер ол жеткілікті үлкен болса. Басқаша айтқанда, кез келген
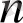 ұзындықты жол өте ұзақ жолдың бастапқы бөлігі сияқты қарастырылуы мүмкін және сондықтан соңғы жолдың ұзындығын анықтау қажет емес. Интуитивті және формальды көзқарас тұрғысынан тәжірибенің шектеусіз тізбегін қарастырған ыңғайлы, бірақ бұл қарапайым оқиғалардың саналымсыз кеңістіктерді қолдануға алып келер еді. Сондықтан әрі қарай қарапайым оқиғалар кеңістігін құраушы
ұзындықты жол өте ұзақ жолдың бастапқы бөлігі сияқты қарастырылуы мүмкін және сондықтан соңғы жолдың ұзындығын анықтау қажет емес. Интуитивті және формальды көзқарас тұрғысынан тәжірибенің шектеусіз тізбегін қарастырған ыңғайлы, бірақ бұл қарапайым оқиғалардың саналымсыз кеңістіктерді қолдануға алып келер еді. Сондықтан әрі қарай қарапайым оқиғалар кеңістігін құраушы
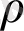 жолдардың ұзындығы біздің формулаларымызда кездесетін қадамдардың санынан көп деп есептейтін боламыз. Бұған қоса, біз өзімізге
жолдардың ұзындығы біздің формулаларымызда кездесетін қадамдардың санынан көп деп есептейтін боламыз. Бұған қоса, біз өзімізге
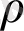 - ның бар екенін ұмытуға мүмкіндік береміз.
- ның бар екенін ұмытуға мүмкіндік береміз.
Біздің дипломдық жұмысымыздың тақырыбы бойынша берілген әдебиеттер тізімі өте ауқымды және кейде ол оқырманды шатастыруы мүмкін. Біздің ұсынып отырған теориямыздың қарапайымдылығы соншалық, бұған дейінгі олардың шынайы табиғи түсініктерін шешу қаншалықты қиын жұмыс болғанын ешкім ешқашан күдіктенуі мүмкін емес. Мысалы, бұрынғы терең әдістермен, кейде үлкен тапқырлықпен алынған қарапайым асимптотикалық бағалаулардың нәтижелері [1, (1. 5) ] практикалық тұрғыда көптеген қызықты нәтижелермен қамтылады.
(1. 6 - 1. 8) тараулары жұмысымыздың бірінші бөлігінен тәуелсіз дерлік. Біздің мазмұндауымыз біржақты және кездейсоқ кезулер теориясының бірқатар қызықты аспесктілерін шетте қалдырғанымызды атап көрсету қажет емес шығар. (Потенциялдар теориясы немесе группалар теориясымен байланыстылары сияқты) [1, 402 - б] .
◄ белгісі дәлелдеудің аяқталғанын немесе мысалдың соңын білдіреді.
Диплом жұмысының құрылым: Диплом жұмысы кіріспеден, 2 бөлімнен, қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады.
- кеңістігіндегі кездейсоқ кезу
1. 1 Негізгі ұғымдар мен белгілері
Бұл жұмыста барлық жерде
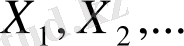 ол ешбір жартылай осьте шоғырланбаған бірдей
ол ешбір жартылай осьте шоғырланбаған бірдей
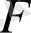 үлестірілген тәуелсіз кездейсоқ шамалардың мағынасы болады. (егер
үлестірілген тәуелсіз кездейсоқ шамалардың мағынасы болады. (егер
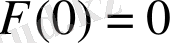 немесе
немесе
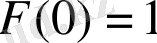 болғанда, қалпына келтіру теориясымен қамтылады) .
болғанда, қалпына келтіру теориясымен қамтылады) .
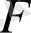 үлестірілімі арқылы жасалған кездейсоқ кезу - кездейсоқ шамалардың тізбегі
үлестірілімі арқылы жасалған кездейсоқ кезу - кездейсоқ шамалардың тізбегі
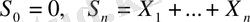 . (1. 1. 1)
. (1. 1. 1)
Кейде біз берілген
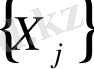 тізбегінің
тізбегінің
 кесіндісін қарастырамыз. Оның
кесіндісін қарастырамыз. Оның
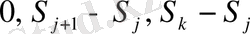 дербес қосындылары кездейсоқ кезудің кесінділері деп аталатын болады. Көрсеткіштер көбіне уақытша параметрлердің мәні ретінде қарастырылады. Осылайша,
дербес қосындылары кездейсоқ кезудің кесінділері деп аталатын болады. Көрсеткіштер көбіне уақытша параметрлердің мәні ретінде қарастырылады. Осылайша,
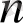 мезеті барлық кездейсоқ кезуді өткен кесінді және қалған кесінді деп бөледі.
мезеті барлық кездейсоқ кезуді өткен кесінді және қалған кесінді деп бөледі.
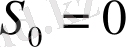 болғандықтан, кездейсоқ кезу 0 де басталады.
болғандықтан, кездейсоқ кезу 0 де басталады.
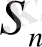 тізбегінің барлық мүшесіне тұрақты
тізбегінің барлық мүшесіне тұрақты
 қоса отырып,
қоса отырып,
 нүктесінен басталатын кездейсоқ кезуді аламыз. Осылайша,
нүктесінен басталатын кездейсоқ кезуді аламыз. Осылайша,
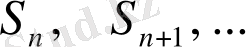 -
-
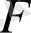 үлестірімі арқылы жасалған және
үлестірімі арқылы жасалған және
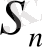 - нен басталатын кездейсоқ кезу.
- нен басталатын кездейсоқ кезу.
Әдебиетте бірнеше мәрте
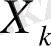 сәйкесінше
сәйкесінше
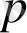 және
және
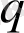 ықтималдықтарымен +1 және -1 мәндерін қабылдайтын кездейсоқ кезулер қарастырылады. Мұндай кезулер кезінде әрбір келесі рекордты мән алдыңғыдан +1 ге артып отырады және тізбектелген баспалдақты нүктелер өз алдына қарапайым 1, 2, . . . арқылы бірінші уақытылы өтуді білдіреді. Біз қабылдаған терминологияда баспалдақты биіктік алдын ала белгілі болатынын, тек онда тізбекті баспалдақты нүктелер арасындағы күтілген уақытты оқытуды талап етеді деп айта аламыз. Олар +1 арқылы өтетін бірінші уақытылы өтудің үлестірілімдері сияқты тәуелсіз кездейсоқ шамалар болып табылады. Жасаушы функция мынадай түрге ие:
ықтималдықтарымен +1 және -1 мәндерін қабылдайтын кездейсоқ кезулер қарастырылады. Мұндай кезулер кезінде әрбір келесі рекордты мән алдыңғыдан +1 ге артып отырады және тізбектелген баспалдақты нүктелер өз алдына қарапайым 1, 2, . . . арқылы бірінші уақытылы өтуді білдіреді. Біз қабылдаған терминологияда баспалдақты биіктік алдын ала белгілі болатынын, тек онда тізбекті баспалдақты нүктелер арасындағы күтілген уақытты оқытуды талап етеді деп айта аламыз. Олар +1 арқылы өтетін бірінші уақытылы өтудің үлестірілімдері сияқты тәуелсіз кездейсоқ шамалар болып табылады. Жасаушы функция мынадай түрге ие:
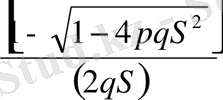 , (1. 1. 2)
, (1. 1. 2)
мұндағы,
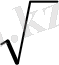 - оң түбірді білдіреді.
- оң түбірді білдіреді.
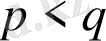 болғанда, бірінші уақытылы өту меншіксіз кездейсоқ шамалар болады. Өйткені ықтималдығы оң мән қабылдауы мүмкін;
болғанда, бірінші уақытылы өту меншіксіз кездейсоқ шамалар болады. Өйткені ықтималдығы оң мән қабылдауы мүмкін;
 - ға тең.
- ға тең.
Бір рекордтық мән жаңа рекордтық мәнді қабылдамас бұрын бірнеше рет қайталануы мүмкін. Бұндай салыстырмалы максимум нүктелері әлсіз баспалдақты нүктелер деп аталады. (бірінші әлсіз баспалдақты нүкте Бернулли қарапайым кездейсоқ кезуінде
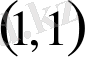 нүктесі болады) .
нүктесі болады) .
Осындай ескертулерден кейін формальды түрде баспалдақты шамаларды енгіземіз. Анықтама теңсіздіктерге негізделген, сондықтан төрт мүмкіндікке сәйкес баспалдақты шамалардың төрт түрі бар, яғни
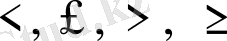 . Бұл түсінікті терминдермен өрнектелетін қос жіктеуге келтіріледі: өспелі және кемімелі (егер нүкте жайында айтылған жағдайда, біз «жоғарғы» және «төменгі» терминдерін пайдаланамыз), қатаң және әлсіз. Қосу және азайту, максимум және минимум секілді өспелі және кемімелі шамалар да симметриялы байланысты. Бірақ қатаң және әлсіз шамалар арасындағы айырмашылық анықтамалар мен белгілерде қиындық тудырады. Бұдан шығудың ең оңай жолы тек
. Бұл түсінікті терминдермен өрнектелетін қос жіктеуге келтіріледі: өспелі және кемімелі (егер нүкте жайында айтылған жағдайда, біз «жоғарғы» және «төменгі» терминдерін пайдаланамыз), қатаң және әлсіз. Қосу және азайту, максимум және минимум секілді өспелі және кемімелі шамалар да симметриялы байланысты. Бірақ қатаң және әлсіз шамалар арасындағы айырмашылық анықтамалар мен белгілерде қиындық тудырады. Бұдан шығудың ең оңай жолы тек
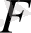 үздіксіз үлестірімін қарастыру болып табылады. Өйткені, осы жағдайда ғана қатаң және әлсіз шамалар бір ықтималдығымен бір - біріне тең. Әуелі дәл осы жолды таңдауға болады және қатаң мен әлсіз баспалдақты шамалар арасында айырмашылық жасамауға болады, бірақ мұндай айырмашылықтар бір жағынан жалпы теорияда және басқа жағынан тиын лақтыру ойыны сияқты мысалдарда да шарасыз.
үздіксіз үлестірімін қарастыру болып табылады. Өйткені, осы жағдайда ғана қатаң және әлсіз шамалар бір ықтималдығымен бір - біріне тең. Әуелі дәл осы жолды таңдауға болады және қатаң мен әлсіз баспалдақты шамалар арасында айырмашылық жасамауға болады, бірақ мұндай айырмашылықтар бір жағынан жалпы теорияда және басқа жағынан тиын лақтыру ойыны сияқты мысалдарда да шарасыз.
Қажетті ұғымдар мен келісімдерді енгізу үшін, алдымен өспелі қатаң баспалдақты шамаларды қарастырайық. Сосын біз әлсіз баспалдақты шамалар теориясы қатаң баспалдақты шамалар теориясының қарапайым салдыры екенін көрсетеміз. Кемімелі баспалдақты шамалар жеке теорияны қажет етпейді. Осылайша, біз заңды түрде, өспелі қатаң баспалдақты шамаларды қарастыра аламыз, және шатасу қауіпі болмаған жағдайда «өспелі» және «қатаң» атауларын пайдаланбауға болады.
Өспелі қатаң баспалдақты шамалар.
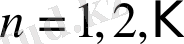 (ноль қабылданбайды) үшін
(ноль қабылданбайды) үшін
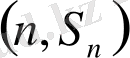 нүктелерінің тізбегін қарастырайық.
нүктелерінің тізбегін қарастырайық.
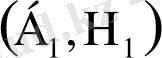 алғашқы қатаң жоғарғы баспалдақты нүктесі - бұл
алғашқы қатаң жоғарғы баспалдақты нүктесі - бұл
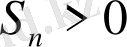 болатындай, көрсетілген тізбектің алғашқы мүшесі. Басқаша айтқанда,
болатындай, көрсетілген тізбектің алғашқы мүшесі. Басқаша айтқанда,
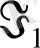 - төмендегі арақатынастармен анықталатын, оң (ашық) жарты осіне өткендегі бірінші мезет.
- төмендегі арақатынастармен анықталатын, оң (ашық) жарты осіне өткендегі бірінші мезет.
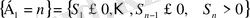 , (1. 1. 3)
, (1. 1. 3)
ал
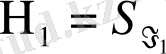 .
.
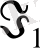 биіктігі бірінші баспалдақты мезет деп аталады, ал
биіктігі бірінші баспалдақты мезет деп аталады, ал
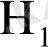 бірінші баспалдақты биіктік. Егер (1. 1. 3) формуласында ешбір оқиға басталмаса, онда бұл кездейсоқ шамалар анықталмаған болып қалады. Сондықтан екеуіде меншіксіз болуы мүмкін.
бірінші баспалдақты биіктік. Егер (1. 1. 3) формуласында ешбір оқиға басталмаса, онда бұл кездейсоқ шамалар анықталмаған болып қалады. Сондықтан екеуіде меншіксіз болуы мүмкін.
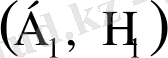 ортақ үлестірімі үшін біз
ортақ үлестірімі үшін біз
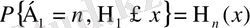 (1. 1. 4)
(1. 1. 4)
белгілеуін аламыз. Онда маргиналдық үлестірім
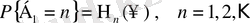 (1. 1. 5)
(1. 1. 5)
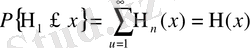 (1. 1. 6)
(1. 1. 6)
теңдеулерімен беріледі. Екі кездейсоқ шамада ақауы бірдей болады, дәлірек айтсақ
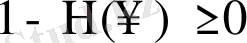 .
.
Бірінші баспалдақты мезеттен кейінгі кездейсоқ кезудің кесіндісі барлық кездейсоқ кезудің дәл ықтималды көшірмесі болып табылады. Оның бірінші баспалдақты нүктесі барлық кездейсоқ кезудің екінші баспалдақты нүктесі болып табылады және
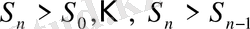 (1. 1. 7)
(1. 1. 7)
өрнегіндей қасиетке ие болады. Біз оны енді солай атаймыз, яғни кездейсоқ кезудің екінші баспалдақты нүктесі деп. Ол
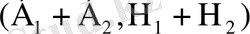 түрде болады. Мұндағы,
түрде болады. Мұндағы,
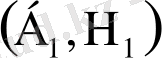 және
және
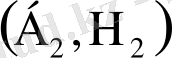 жұптары тәуелсіз және бірдей үлестірілген. Аналогты түрде біз кездейсоқ кезудің үшінші, төртінші және тағы басқа баспалдақ нүктелерін анықтай аламыз. Осылайша, егер ол (1. 1. 7) қатынасын қанағаттандырса,
жұптары тәуелсіз және бірдей үлестірілген. Аналогты түрде біз кездейсоқ кезудің үшінші, төртінші және тағы басқа баспалдақ нүктелерін анықтай аламыз. Осылайша, егер ол (1. 1. 7) қатынасын қанағаттандырса,
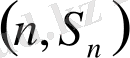 нүктесі жоғарғы баспалдақты нүкте болып табылады.
нүктесі жоғарғы баспалдақты нүкте болып табылады.
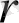 нөмірлі баспалдақты нүкте (егер ол бар болса)
нөмірлі баспалдақты нүкте (егер ол бар болса)
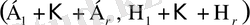 түріне ие болады, мұндағы
түріне ие болады, мұндағы
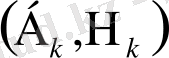 жұптары өзара тәуелсіз және (1. 1. 4) - пен бірдей үлестірімге ие.
жұптары өзара тәуелсіз және (1. 1. 4) - пен бірдей үлестірімге ие.
Белгілерді үнемдеу үшін біз
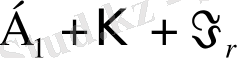 және
және
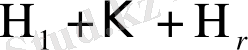 қосындысы үшін ешқандай жаңа әріп енгізбейміз. Олар
қосындысы үшін ешқандай жаңа әріп енгізбейміз. Олар
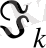 және
және
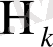 «қалпына келтірулер аралығымен» екі қалпына келтіру процесін құрайды. (Үзілгендер болуы мүмкін) . Кездейсоқ кезуде тек
«қалпына келтірулер аралығымен» екі қалпына келтіру процесін құрайды. (Үзілгендер болуы мүмкін) . Кездейсоқ кезуде тек
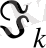 уақыттың рөлін атқарады. Айта кететіні, баспалдақты нүктелердің өзі екі өлшемді процессті қалпына келтіруді құрайды.
уақыттың рөлін атқарады. Айта кететіні, баспалдақты нүктелердің өзі екі өлшемді процессті қалпына келтіруді құрайды.
Баспалдақты биіктіктің орта санын анықтайтын өлшемін
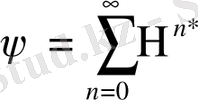 (1. 1. 8)
(1. 1. 8)
деп белгілейік (мұндағы
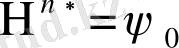 ) .
) .
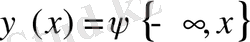 теңдеуімен берілетін сәйкес меншіксіз үлестірім функциясы
теңдеуімен берілетін сәйкес меншіксіз үлестірім функциясы
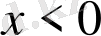 болғанда 0-ге тең, ал оң
болғанда 0-ге тең, ал оң
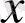 үшін
үшін
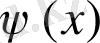 функциясы
функциясы
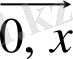 полюсінде баспалдақты нүктелердің орта санының қосуы бірге тең (уақыт шектелмейді) . Біз білетіндей, барлық
полюсінде баспалдақты нүктелердің орта санының қосуы бірге тең (уақыт шектелмейді) . Біз білетіндей, барлық
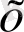 үшін
үшін
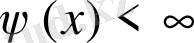 және меншіксіз баспалдақты шамалар жағдайында
және меншіксіз баспалдақты шамалар жағдайында
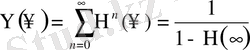 . (1. 1. 9)
. (1. 1. 9)
Ақырында, нөлдегі бірлік масса мен атомдық үлестірім үшін
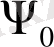 белгілеуін енгіземіз; осылайша, кез келген
белгілеуін енгіземіз; осылайша, кез келген
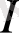 интервалы үшін
интервалы үшін
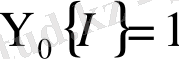 , егер
, егер
 болса, олай болмаған жағдайда
болса, олай болмаған жағдайда
 . (1. 1. 10)
. (1. 1. 10)
Өспелі әлсіз баспалдақты шамалар.
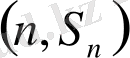 нүктесі әлсіз (жоғарғы) баспалдақты нүкте болады сонда тек қана сол жағдайда ғана, егер
нүктесі әлсіз (жоғарғы) баспалдақты нүкте болады сонда тек қана сол жағдайда ғана, егер
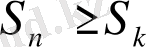 болса (
болса (
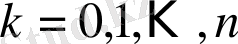 ) . Қатаң және әлсіз баспалдақты шамаларды қатар оқитын боламыз және біз жүйелі түрде сол әріптердің жоғарынан сызық салу арқылы әлсіз шамаларды белгілейміз. Сонымен
) . Қатаң және әлсіз баспалдақты шамаларды қатар оқитын боламыз және біз жүйелі түрде сол әріптердің жоғарынан сызық салу арқылы әлсіз шамаларды белгілейміз. Сонымен
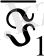 -
-
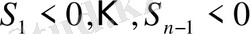 , бірақ
, бірақ
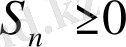 болатындай
болатындай
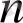 - нің ең кіші индексі. Басында айтылғандай, егер
- нің ең кіші индексі. Басында айтылғандай, егер
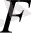 үлестірімі үздіксіз болса, онда қатаң және әлсіз шамаларды ажыратуды қажет етпейді. Жалпы жағдайда
үлестірімі үздіксіз болса, онда қатаң және әлсіз шамаларды ажыратуды қажет етпейді. Жалпы жағдайда
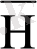 әлсіз баспалдақты биіктіктің үлестірімін
әлсіз баспалдақты биіктіктің үлестірімін
 үлестірім терминдерімен оңай көрсетуге болады. Бұл бізге (1. 1. 6) -да анықталған бір үлестіріммен шектелуге мүмкіндік береді.
үлестірім терминдерімен оңай көрсетуге болады. Бұл бізге (1. 1. 6) -да анықталған бір үлестіріммен шектелуге мүмкіндік береді.
Бірінші әлсіз баспалдақты нүкте бірінші қатаң баспалдақты нүктеге ұқсас, тек теріс мән арқылы өткендегі кездейсоқ кезудің нолге оралғандағы жағдайынан басқа; бұл жағдайда
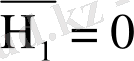 , және біз оны
, және біз оны
 . Осылайша,
. Осылайша,
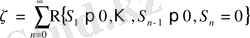 . (1. 1. 11)
. (1. 1. 11)
(Егер
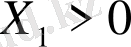 болса, бұл оқиға орындалуы мүмкін емес. Демек,
болса, бұл оқиға орындалуы мүмкін емес. Демек,
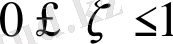 ) .
) .
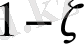 ықтималдығымен бірінші қатаң баспалдақты нүкте бірінші әлсіз баспалдақты нүктемен сәйкес келеді. Демек,
ықтималдығымен бірінші қатаң баспалдақты нүкте бірінші әлсіз баспалдақты нүктемен сәйкес келеді. Демек,
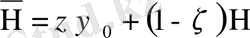 . (1. 1. 12)
. (1. 1. 12)
Басқаша айтқанда, бірінші әлсіз баспалдақты биіктіктің үлестірімі,
 үлестірімі мен нольде шоғырланған атомдық үлестірімінің қоспасы болады.
үлестірімі мен нольде шоғырланған атомдық үлестірімінің қоспасы болады.
Мысал. Бернуллидің кездейсоқ кезуінде бірінші әлсіз баспалдақты биіктік 1-ге тең сонда тек қана сонда, егер бірінші қадам +1 нүктесіне келгенде. Егер бірінші қадам -1 нүктесіне келсе, онда 0-ге қайтып келу (шартты) ықтималдығы 1-ге тең, егер
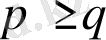 болса, қарсы жағдайда
болса, қарсы жағдайда
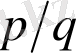 тең. Бірінші жағдайда
тең. Бірінші жағдайда
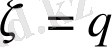 , екіншісінде
, екіншісінде
 . Мүмкін баспалдақты биіктіктер 1-ге және 0-ге тең, және олардың ықтималдығы
. Мүмкін баспалдақты биіктіктер 1-ге және 0-ге тең, және олардың ықтималдығы
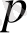 және
және
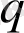 болады (
болады (
 ) . Онда
) . Онда
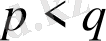 болғанда екі ықтимал да
болғанда екі ықтимал да
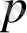 - ға тең. Соңғы жағдайда баспалдақты ықтимал тәуелсіз кездейсоқ шама болады. ◄
- ға тең. Соңғы жағдайда баспалдақты ықтимал тәуелсіз кездейсоқ шама болады. ◄
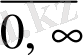 -не бірінші түсуіне дейінгі кездейсоқ кезудің
-не бірінші түсуіне дейінгі кездейсоқ кезудің
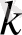 рет нольге оралу ықтималдығы
рет нольге оралу ықтималдығы
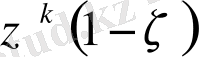 тең. Осындай оралулардың математикалық күтім саны
тең. Осындай оралулардың математикалық күтім саны
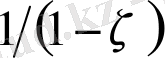 - ге тең. Бұл шама бізге әрбір баспалдақты биіктіктің күтілген еселігін береді (яғни оның келесі баспалдақты биіктіктің пайда болатын саны) . Демек,
- ге тең. Бұл шама бізге әрбір баспалдақты биіктіктің күтілген еселігін береді (яғни оның келесі баспалдақты биіктіктің пайда болатын саны) . Демек,
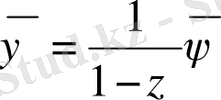 . (1. 1. 13)
. (1. 1. 13)
Осы арақатынастың қарапайымдылығы анық
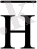 үлестірімін қолданбауға мүмкіндік береді.
үлестірімін қолданбауға мүмкіндік береді.
Кемімелі баспалдақты шамалар. Қатаң және әлсіз кемімелі баспалдақты шамалар симметриялы түрде анықталады, яғни
 белгісін
белгісін
 белгісіне ауыстыру арқылы. Арнайы белгілеулерді қажет ететін жағдайда біз кемімелі шамаларды жоғары «азайту» индексімен белгілейтін боламыз. Сонымен, бірінші қатаң төменгі баспалдақты нүктес
белгісіне ауыстыру арқылы. Арнайы белгілеулерді қажет ететін жағдайда біз кемімелі шамаларды жоғары «азайту» индексімен белгілейтін боламыз. Сонымен, бірінші қатаң төменгі баспалдақты нүктес
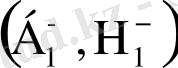 болады және т. с. с.
болады және т. с. с.
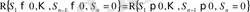 (1. 1. 14)
(1. 1. 14)
болғандақтан,
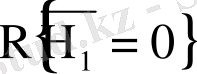 және
және
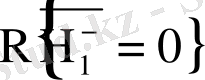 ықтималдықтары өзара тең болады. Осыдан, кемімелі баспалдақты шамалар үшін (1. 1. 12) және (1. 1. 13) формулалары
ықтималдықтары өзара тең болады. Осыдан, кемімелі баспалдақты шамалар үшін (1. 1. 12) және (1. 1. 13) формулалары
 шамасына тәуелді.
шамасына тәуелді.
1. 2 Қосалқылық. Кездейсоқ кезулердің типтері
Тиынды лақтыру кезінде туындайтын флуктуацияның қызықты қасиеттерін тағайындаған болатынбыз. Есептеу барысында, теріс бағытта алынған
 шамаларына негізделген қарапайым комбинаторикалық тұжырымдар қолданылды. Енді дәл осы тәсіл арқылы өте маңызды және жалпыланған нәтижелерге келе аламыз.
шамаларына негізделген қарапайым комбинаторикалық тұжырымдар қолданылды. Енді дәл осы тәсіл арқылы өте маңызды және жалпыланған нәтижелерге келе аламыз.
n
мәнін бекітіп алып,
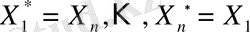 теңдіктері арқылы жаңа
n
кездейсоқ шамаларын еңгіземіз. Сәйкес дербес қосындылар мына түрде
теңдіктері арқылы жаңа
n
кездейсоқ шамаларын еңгіземіз. Сәйкес дербес қосындылар мына түрде
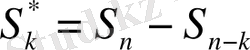 , мұндағы
, мұндағы
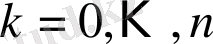 . Ал
. Ал
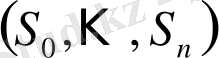 және
және
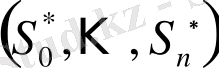 шамаларының ортақ үлестірімдері бір-біріне сәйкес. Сондықтан да
шамаларының ортақ үлестірімдері бір-біріне сәйкес. Сондықтан да
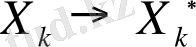 кескіндеуі,
кескіндеуі,
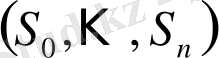 шамасымен байланысқан кез келген
А
оқиғасын бірдей ықтималдықты
шамасымен байланысқан кез келген
А
оқиғасын бірдей ықтималдықты
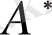 оқиғасына кескіндейді. Осы түрдегі кескіндеуді көз алдымызға елестету қиын емес, өйткені
оқиғасына кескіндейді. Осы түрдегі кескіндеуді көз алдымызға елестету қиын емес, өйткені
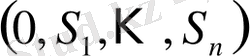 және
және
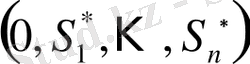 тізбектерінің графигі бір-бірінен тек 180º градусқа бұрыла жалғасып отырады.
тізбектерінің графигі бір-бірінен тек 180º градусқа бұрыла жалғасып отырады.
Мысал. а)
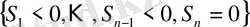 оқиғасына
оқиғасына
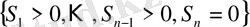 оқиғасы қосалқы болады. Бұл (1. 1. 14) қатынасының ақиқат екенін көрсетеді. Енді біз жоғарыда аталған «көшу» процедурасын (әрекетін), қатаң жоғарғы баспалдақтық нүктені анықтайтын
оқиғасы қосалқы болады. Бұл (1. 1. 14) қатынасының ақиқат екенін көрсетеді. Енді біз жоғарыда аталған «көшу» процедурасын (әрекетін), қатаң жоғарғы баспалдақтық нүктені анықтайтын
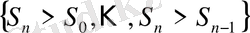 оқиғасына қолданамыз. Қосалқы оқиғалар
оқиғасына қолданамыз. Қосалқы оқиғалар
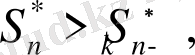
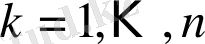 теңсіздіктері арқылы айқындалады. Бірақ,
теңсіздіктері арқылы айқындалады. Бірақ,
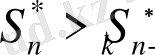 оқиғасы
оқиғасы
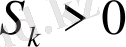 оқиғасына сәйкес келеді. Осылайша, әрбір
оқиғасына сәйкес келеді. Осылайша, әрбір
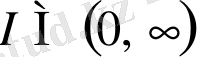 ақырлы интервалы үшін
ақырлы интервалы үшін
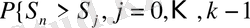 және
және
 =
=
=
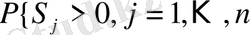 және
және
 . (1. 2. 1)
. (1. 2. 1)
Бұл теңдіктің сол жағы -
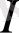 интервалына тиісті абсциссасы мен ординатасы бар болатын баспалдақтық нүктесінің табылу ықтималдығына тең. Ал оң жағы -
n
мезетінде
интервалына тиісті абсциссасы мен ординатасы бар болатын баспалдақтық нүктесінің табылу ықтималдығына тең. Ал оң жағы -
n
мезетінде
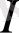 интервалына дәл тию ықтималдығына тең, және де
n
мезетіне дейін тұйық
интервалына дәл тию ықтималдығына тең, және де
n
мезетіне дейін тұйық
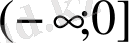 жартытүзуіне ешбір кіріс болмайды деп қабылдаймыз. (1. 2. 1) теңдігін қосындылай отырып, нәтижелерін саралаймыз.
ψ
шамасының (1. 1. 8) анықтамасына сәйкес теңдіктің сол жағы
жартытүзуіне ешбір кіріс болмайды деп қабылдаймыз. (1. 2. 1) теңдігін қосындылай отырып, нәтижелерін саралаймыз.
ψ
шамасының (1. 1. 8) анықтамасына сәйкес теңдіктің сол жағы
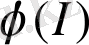 тең болады. Оң жағынан
тең болады. Оң жағынан
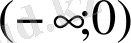 интервалына бірінші рет дәл тигенге дейінгі,
интервалына бірінші рет дәл тигенге дейінгі,
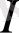 аралығына тию сандарының математикалық күтімін аламыз. Бұл шама ақырлы, өйткені
аралығына тию сандарының математикалық күтімін аламыз. Бұл шама ақырлы, өйткені
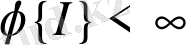 . Осылайша, біз келесі лемманы тағайындадық.
. Осылайша, біз келесі лемманы тағайындадық.
Қосалқылық туралы лемма.
ψ
шамасының екі түсіндірмесі бар. Әрбір ақырлы
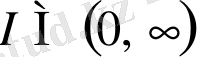 интервалы үшін
интервалы үшін
а)
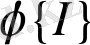 -
-
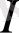 аралығындағы баспалдақтық нүктелер санының математикалық күтімі.
аралығындағы баспалдақтық нүктелер санының математикалық күтімі.
б)
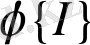 -
-
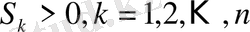 болатындай
болатындай
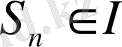 дәл тию санының математикалық күтімі.
дәл тию санының математикалық күтімі.
Басқа жағдайларда, дәлелдеуі терең мағыналы аналитикалық есептеулерді қажет ететін теоремаларды, осы қарапайым лемма көмегімен элементар әдіс арқылы дәлелдеуге мүмкіндік туындады. Лемманың аналитикалық құрылымы айтарлықтай күрделі емес, дегенмен оның тікелей салдарлары таңқаларлықтай нәтижелерге жетелейді.
Мысал. б) Қарапайым кездейсоқ кезу. (1. 1) мысалында сипатталған кездейсоқ кезуінде, ординатасы
k
болатын баспалдақтық нүкте сонда тек сонда ғана бар болады, егер кейбір
n
үшін
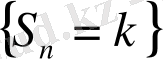 оқиғасы орындалады (бұл оқиғаның ықтималдығы
оқиғасы орындалады (бұл оқиғаның ықтималдығы
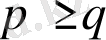 болғанда 1-ге және
болғанда 1-ге және
 болғанда
болғанда
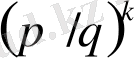 тең) . Қосалқылық леммасы бойынша, оның мағынасы мынадай: Симметриялы кездейсоқ кезуде, бірінші нөлге қайта айналу процессіне дейінгі
тең) . Қосалқылық леммасы бойынша, оның мағынасы мынадай: Симметриялы кездейсоқ кезуде, бірінші нөлге қайта айналу процессіне дейінгі
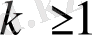 күйіне дәл тигізу санының математикалақ күтімі барлық
k
-лар үшін 1-ге тең болады. Бұл нәтиженің кереметілігі қаншалықты екенін, тиын лақтыру логикалық ойынының терминологиясына пайдаланғаннан соң ұғынуға болады. Біздің тұжырымдауымыз бойынша - нөлдік деңгейге бірінші рет айналғанға дейін Петрдің орташа жинақтық ұтысы ең болмағанда
k
-ның кез келген бір мәнін қабылдар еді. Көп жағдайларда мұндай тұжырым күмән тудырады, дегенмен математикалық есептеу жүргізу арқылы оны тексеріп, көз жеткізуге болады. (Бірінші нөлге қайта айналу уақытының математикалық күтімі туралы осыған дейін жасаған қорытындымыз, енді
k
бойынша қосынды болып табылады)
күйіне дәл тигізу санының математикалақ күтімі барлық
k
-лар үшін 1-ге тең болады. Бұл нәтиженің кереметілігі қаншалықты екенін, тиын лақтыру логикалық ойынының терминологиясына пайдаланғаннан соң ұғынуға болады. Біздің тұжырымдауымыз бойынша - нөлдік деңгейге бірінші рет айналғанға дейін Петрдің орташа жинақтық ұтысы ең болмағанда
k
-ның кез келген бір мәнін қабылдар еді. Көп жағдайларда мұндай тұжырым күмән тудырады, дегенмен математикалық есептеу жүргізу арқылы оны тексеріп, көз жеткізуге болады. (Бірінші нөлге қайта айналу уақытының математикалық күтімі туралы осыған дейін жасаған қорытындымыз, енді
k
бойынша қосынды болып табылады)
Бернуллидің симметриялы кездейсоқ кезуінде (тиын лақтыру) әрбір ±1 мәндері бірлік ықтималдықпен анықталған, бірақ осы оқиғалардың әрқайсысы үшін күту уақытының математикалық күтімі ақырсыз болады. Келесі теоремада - бұл қасиеттің тек тиын лақтыру ойынындағы ерекшелік емес екендігі көрсетіледі, яғни оң және теріс мәндері бірлік ықтималдылықпен анықталатын барлық кездейсоқ кезулер үшін осыған ұқсас тұжырым орынды.
Теорема 1. Кездейсоқ кезудің тек екі типі (түрі) бар:
(І) Тербелуші тип: қалыптастырудың өспелі және кемімелі процестері қайтымды;
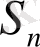 шамасы - ∞ пен + ∞ арасында ауытқиды, және де
шамасы - ∞ пен + ∞ арасында ауытқиды, және де
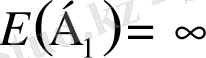 ,
,
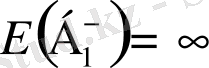 (1. 2. 2)
(1. 2. 2)
(ІІ) Шығымдық тип (айталық, - ∞-ке) : қалыптастырудың өспелі процесі үзілісті; кемімелі процесс меншікті болып табылады;
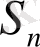 шамасы бірлік ықтималдықпен -∞-ке ұмтылып,
шамасы бірлік ықтималдықпен -∞-ке ұмтылып,
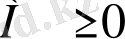 шектік максимумына жетеді; (1. 2. 5) және (1. 2. 7) қатынастары орындалады.
шектік максимумына жетеді; (1. 2. 5) және (1. 2. 7) қатынастары орындалады.
Дәлелдеуі.
(1. 2. 1) тепе-теңдігі қатаң теңсіздіктерді ауыстырған кезде де орындалады.
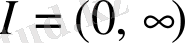 үшін мына өрнекті аламыз:
үшін мына өрнекті аламыз:
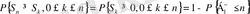 (1. 2. 3)
(1. 2. 3)
Теңдіктің сол жағы -
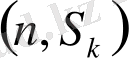 мәнінің әлсіз жоғарғы баспалдақтық нүкте болуының ықтималдығы. Бұл ықтималдықтардың қосындысы
мәнінің әлсіз жоғарғы баспалдақтық нүкте болуының ықтималдығы. Бұл ықтималдықтардың қосындысы
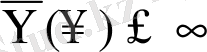 , және де (1. 1. 13) теңдігіне сүйене отырып
, және де (1. 1. 13) теңдігіне сүйене отырып
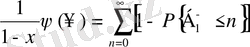 (1. 2. 4)
(1. 2. 4)
аламыз.
Егер кемімелі баспалдақтық процесс меншіксіз болса, онда қатар мүшелері нөлге ұмтылмайды және қатар жинақсыз болады. Бұл жағдайда
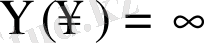 ; демек өспелі баспалдақтық процесс қайтымды деген сөз. Осылайша, біз интуитивті айқын факттың аналитикалық дәлелдемесін алдық: екі баспалдақтық процестердің, яғни өспелі де, кемімелі де процестер үзілісті болуы мүмкін емес.
; демек өспелі баспалдақтық процесс қайтымды деген сөз. Осылайша, біз интуитивті айқын факттың аналитикалық дәлелдемесін алдық: екі баспалдақтық процестердің, яғни өспелі де, кемімелі де процестер үзілісті болуы мүмкін емес.
Егер
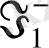 шамасы меншікті болса, онда (1. 2. 4) формуласы
шамасы меншікті болса, онда (1. 2. 4) формуласы
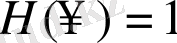 жағдайында (1. 2. 5) -ке түрленеді:
жағдайында (1. 2. 5) -ке түрленеді:
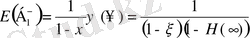 . (1. 2. 5)
. (1. 2. 5)
Көріп отырғандай,
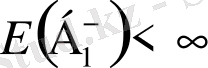 орындалады сонда, тек сонда ғана егер
орындалады сонда, тек сонда ғана егер
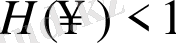 болса, яғни
болса, яғни
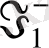 өспелі баспалдақтық шамасы меншікті болмаған жағдайында. Демек, не осы шамалардың бірі меншіксіз болады, не (1. 2. 2) өрнегі орындалады.
өспелі баспалдақтық шамасы меншікті болмаған жағдайында. Демек, не осы шамалардың бірі меншіксіз болады, не (1. 2. 2) өрнегі орындалады.
Егер
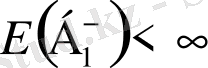 болса, онда қалыптастырудың өспелі процесі үзілісті. Бірлік ықтималдықпен ақырғы баспалдақтық нүктенің бар болатынын анықтай аламыз және мына максимум мәні шектелген:
болса, онда қалыптастырудың өспелі процесі үзілісті. Бірлік ықтималдықпен ақырғы баспалдақтық нүктенің бар болатынын анықтай аламыз және мына максимум мәні шектелген:
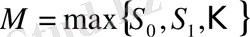 (1. 2. 6)
(1. 2. 6)
n
-ші баспалдақтық нүкте бар болсын делік, онда оның ақырғы болуының ықтималдығы
 тең. Сондықтан
тең. Сондықтан
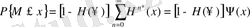 . (1. 2. 7)
. (1. 2. 7)
Келесі теоремаға көшпес бұрын мынадай белгілеулерді келісіп алайық,
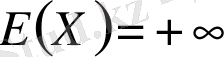 , егер сәйкес интеграл тек қана +∞-те жинақсыз болса, және де
, егер сәйкес интеграл тек қана +∞-те жинақсыз болса, және де
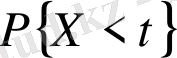 , егер функция (-∞, 0) аралығында интегралданса.
, егер функция (-∞, 0) аралығында интегралданса.
Теорема 2.
(І) Егер
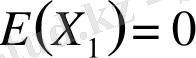 , онда
, онда
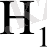 мен
мен
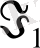 - меншікті шамалар және
- меншікті шамалар және
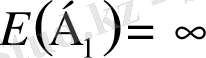 .
.
(ІІ) Егер
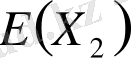 ақырлы әрі оң болса, онда
ақырлы әрі оң болса, онда
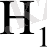 мен
мен
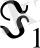 меншікті шамаларның ақырлы математикалық күтімдері бар және
меншікті шамаларның ақырлы математикалық күтімдері бар және
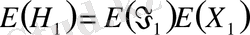 . (1. 2. 8)
. (1. 2. 8)
Кездейсоқ кезу +∞-ке бағытталады.
(ІІІ) Егер
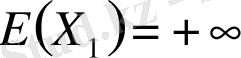 , онда
, онда
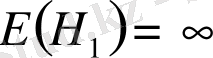 және кездейсоқ кезу +∞-ке бағытталады.
және кездейсоқ кезу +∞-ке бағытталады.
(IV) Қалған жағдайларда, не кездейсоқ кезу -∞-ке бағыт алады (демек,
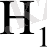 мен
мен
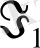 шамалар меншіксіз), немесе
шамалар меншіксіз), немесе
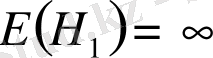 .
.
Дәлелдеуі. Егер n саны k - сыншы баспалдақтық мезетпен сәйкес болса, онда келесі теңбе-теңдік орынды
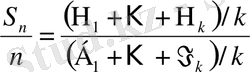 . (1. 2. 9)
. (1. 2. 9)
Енді қатаңданған үлкен сандар заңы
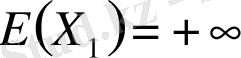 жағдайында да қолданымды екенін ескере кетейік, оны мысалдар арқылы көруге болады.
жағдайында да қолданымды екенін ескере кетейік, оны мысалдар арқылы көруге болады.
(І)
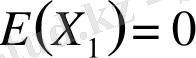 болсын.
k
→∞ ұмтылғанда, (1. 2. 9) өрнегінің сол жағы 0-ге бағытталады. Яғни, бөлшек бөлімі шексіздікке ұмтылады екен. Сондықтан,
болсын.
k
→∞ ұмтылғанда, (1. 2. 9) өрнегінің сол жағы 0-ге бағытталады. Яғни, бөлшек бөлімі шексіздікке ұмтылады екен. Сондықтан,
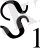 - меншікті шама және
- меншікті шама және
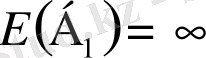 .
.
(ІІ) Егер
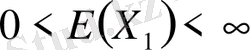 болса, онда қатаңданған үлкен сандар заңы бойынша кездейсоқ кезу ∞-ке ұласады. (1. 2. 5) формуласын ескерсек,
болса, онда қатаңданған үлкен сандар заңы бойынша кездейсоқ кезу ∞-ке ұласады. (1. 2. 5) формуласын ескерсек,
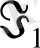 - меншіктішама және
- меншіктішама және
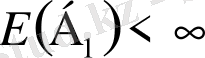 . Сондықтан (1. 2. 9) теңдігіндегі бөлшектің алымы мен бөлімі ақырлы шекке ұмтылады және теоремадан үлкен сандар заңына қайшы (1. 2. 8) өрнегі шығады.
. Сондықтан (1. 2. 9) теңдігіндегі бөлшектің алымы мен бөлімі ақырлы шекке ұмтылады және теоремадан үлкен сандар заңына қайшы (1. 2. 8) өрнегі шығады.
(ІІІ) Егер
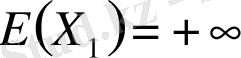 , онда ұқсас тұжырымдар бойынша
, онда ұқсас тұжырымдар бойынша
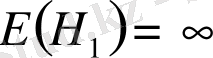 екенін көрсетуге болады.
екенін көрсетуге болады.
(IV) Қалған жағдайларда, егер
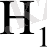 - меншікті шама және
- меншікті шама және
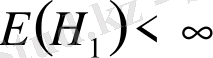 болса, онда кездейсоқ кезу -∞-ке ұмтылатынын көрсете аламыз. Кездейсоқ кезудің келесі қадамын қарастырайық,
болса, онда кездейсоқ кезу -∞-ке ұмтылатынын көрсете аламыз. Кездейсоқ кезудің келесі қадамын қарастырайық,
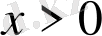 болғанда
болғанда
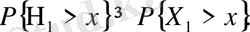 (1. 2. 10)
(1. 2. 10)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz