Бірөлшемді тікбұрышты потенциал шұңқырдағы бөлшек

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Жоспар

Кіріспе3

1. Бірөлшемді тікбұрышты потенциал шұңқырдағы бөлшек4

2. . Кванттық механика негіздері6

30. 5. Гармониялық осцилятор12

Қорытынды14

Пайдаланған әдебиеттер15

Кіріспе

Соңғы жылдары наноқұрылымдық жартылай өткізгіш қабықшаларының қолданылу аясының кеңеюіне байланысты олардың физикалық қасиеттерін өлшеу қазіргі физиканың орталық мәселесіне айналды. Наноқұрылымдық жартылай өткізгіштер жылдам жұмыс істейтін есептеуіш техниканы, оптоэлектрониканың, фотониканың жаңа тиімді құралдарын жасауда және дамытуда үмітті материал болып табылады. Наноқұрылымдық жартылай өткізгіштердің маңызды жетістігі сол - олардың геометриялық өлшемі мен конфигурациясын өзгерту арқылы жүйенің қасиеттерін басқаруға болады. Құрылымның параметрлерін басқарудың, бәрінен бұрын қуатты тасымалдаушылар мен фонондардың энергетикалық спектрін және наноқұрылымдардың оптикалық қасиеттерін басқарудың кең мүмкіндіктері ашылады.

Потенциалдық шұңқыр - бөлшектер өзара әсерлескенде бөлшектердің потенциалдық энергиясының оның сыртындағыдан аз болатын физикалық табиғаты анықталатын кеңістіктің шектеулі бөлігі. Потенциалдық шұңқырдың формасы мен оның мөлшерлері бөлшектердің өзара әрекеттесуінің физикалық табиғатымен анықталады. Атом электронының ядроға тартылуын сипаттайтын кулондық потенциалдық шұңқыр - маңызды жағдай болып есептеледі. “Потенциалдық шұңқыр” түсінігі атомдық және молекулалық физикада, қатты денелер мен атомдық ядро физикасында кең қолданылады.

1. Бірөлшемді тікбұрышты потенциал шұңқырдағы бөлшек

Бір өлшемді потенциалдық шұңқыр ішіндегі электрон үшін Шредингер теңдеуінің шешімін қарастыралық. Мұндай жағдай өте қарапайым, әрі жасанды. Дегенмен, ол Шредингер теңдеуінің және оның шешімдерінің негізгі ерекшеліктерін жеткілікті түрде оңай көрсетуге мүмкіндік береді.

Шексіз терең бір өлшемді потенциалдық шұңқырдағы бөлшек үшін меншікті энергия мәндері мен бұларға сәйкес меншікті функцияларды табайық. Массасы т бөлшек (электрон) тек х осі бойымен қозғала алатын болсын; және қозғалыс бөлшекті өткізбейтін 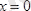және 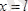қабырғаларымен шектелген болсын. Осы жағдайда U потенциалдық энергияның түрі 1а-суретте көрсетілгендей: 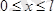болғанда 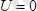, 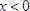және 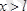болғанда 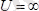болады.

Бір өлшемді есептер жағдайында стационарлық күйлер үшін Шредингер теңдеуі былай өрнектеледі:

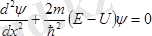. (4)

Потенциалдық шұңқырдан бөлшек шыға алмайды. Сондықтан бөлшектің шұңқыр сыртында табылу ықтималдығы нөлге тең. Осыған сәйкес 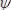толқындық функция да шұңқырдан тыс аймақтарда нөлге тең болады. Үздіксіздік шартынан 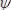шұңқыр шекарасында да нөлге тең болуға тиіс, яғни

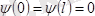. (5)

Осы шартта (4) теңдеуінің шешшімдері қанағаттандыруға тиіс. Шұңқыр ішінде 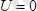болғандықтан (4) Шредингер теңдеуі осы жағдайда былай жазылады:

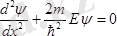. (6)

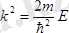белгілеуін енгізіп, тербелістер

теориясынан белгілі теңдеу алынады:

1-сурет .

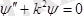Бұл теңдеудің жалпы шешімі белгілі, ол мынадай:

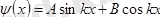. (7)

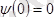шекаралық шартынан 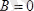болғандығы шығады; демек

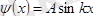(7а)

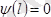шартынан 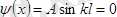болатындығы шығады; бұл егер

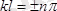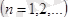, (8)

болған жағдайда ғана мүмкін болады. (8) теңдіктің екі жағын да квадраттап және 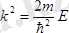өрнегін ескеріп, бөлшек энергиясының мәнін табамыз:

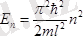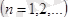, . (9)

Демек, Е энергия дискреттік мәндер жиынтығын қабылдайды. (9) өрнек қарастырылған потенциалдық шұңқырдағы бөлшектің энергиясын анықтайды. Шұңқыр ішінде бөлшектің потенциалдық энергиясы болмайтындықтан, толық энергиясы кинетикалық энергияға тең болады. Бөлшек энергиясы квантталған, яғни бөлшек энергиясы тек белгілі дискреттік мәндер қабылдай алады, бұлар меншікті мәндер болып табылады. Осы меншікті мәндер энергия деңгейлерінің жүйесін құрайды. 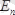деңгейге сәйкес келетін n бүтін саны осы деңгейдің кванттық саны деп аталады. 1б-суретте бөлшектің бірнеше энергия деңгейлерінің орналасуы көрсетілген. Ең аз энергиясы бар күй - негізгі, қалғандары - қозған күй деп аталады. Көрші деңгейлердің аралығы былай анықталады:

ғни бөлшек массасы және шұңқыр ені кеміген сайын 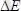арта түседі. n артқанда 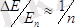қатынасы кемиді. Осыдан кванттық күйлердің дискреттігі кіші n жағдайында айқын байқалады да, үлкен n жағдайында бәсеңдеп, іс жүзінде жоғалады.

Шұңқырдағы бөлшектің энергиясы нөлге тең болуы мүмкін емес. Егер бөлшек энергиясы нөлге тең болса, онда оның толқындық функциясы да шұңқырдың кез келген нүктесінде нөл болар еді. Ал бұл бөлшектің шұнқырда болуы мүмкін емес деген мағына береді. Бөлшек энергиясының нөлге тең болмауы және мүмкін мәндерінің белгілі дискретті мәндермен шектелуі кванттық механикаға тән нәтижелер. Классикалық механикада энергия кез келген мәнге, соның ішінде нөлге тең бола алады. Анықталмағандық принципі бойынша да Е =0 энергия мәні келіспейді.

2. . Кванттық механика негіздері

Микробөлшектердің қозғалыс заңдылықтарын зерттейтін физиканың бөлімін кванттық механика деп атайды.

Элементар бөлшектерді және осы бөлшектердің аз санынан тұратын денелерді микробөлшектер деп атаймыз. Француз ғалымы де Бройль жарықтың екі жақтылық қасиеті электронға да орындалады деген болжам ұсынды, яғни электронның механикалық қозғалысына толқындық қасиет сәйкес келеді және бұл толқынның ұзындығы келесі формуламен анықталады:

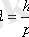немесе ,

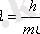мұндағы: р - дене импульсы, 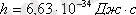-Планк тұрақтысы.

Бұл өрнек де Бройль формуласы деп аталады.

Ал бөлшектің кинетикалық энергиясы 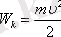екенін ескерсек, онда де Бройльдің толқын ұзындығы кинетикалық энергия арқылы келесі түрде өрнектеледі:

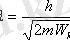Потенциалдар айырмасы 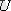-ға тең үдетуші электр өрісінен өткен электронның энергиясы:

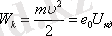
Соңғы өрнекті ескере отырып де Бройль формуласын келесі түрде өрнектеуге болады:

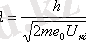мұндағы: .

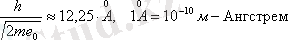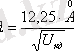Американ ғалымы Томсон жұқа металл фольгалардан шапшаң электрондарды өткізгенде экранда дифракциялық көрініс бақылады.

Бұл дифракциялық көрініс Брэгг-Вульф шартымен сипатталады:

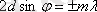
Кванттық механикада кез-келген микробөлшектің қозғалысына толқындық қозғалыс сәйкес келеді және бұл толқындық қозғалыс сол бөлшектің де Бройльдық толқын ұзындығымен сипатталады.

де Бройль толқынының амплитудасының квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды. Микробөлшектің кеңістіктің берілген нүктеде болу ықтималдығын анықтау үшін кеңістік пен уақыттың функциясы толқындық функция енгізілген.

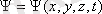функциясы толқындық функция немесе пси функция деп аталады.

Пси функциясының модулінің квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды.

Толқындық функция келесі шартты қанағаттандыруы қажет:

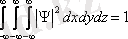Бұл шарт нормалану шарты деп аталады.

Гейзенберг анықталмаушылық принципі

Өзара байланысқан шамаларды анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды.

Кез-келген А және В байланысқан шамалары үшін Гейзенбергтің анықталмаушылық принципі келесі түрде жазылады:

.

Координата мен импульс үшін Гейзенбергтің анықталмаушылық принципі.

Координата мен импульсті анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды, яғни

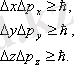
Энергия мен уақыт үшін Гейзенбергтің анықталмаушылық принципі:

мұндағы: 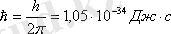-Планк тұрақтысы.

30. 2. Шредингер теңдеуі

Релятивистік емес кванттық механиканың негізгі теңдеуін неміс ғалымы Шредингер алды. Сондықтан бұл теңдеу Шредингер теңдеуі деп аталады.

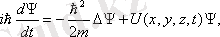
мұндағы: 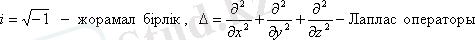, 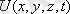- күштік өрістегі бөлшектің потенциалдық энергиясы.

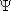- функциясына қойылатын шарттар:

1. 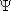- функциясы шекті, үздіксіз, бір мәнді болу қажет;

2. 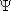- функциясы уақыт пен координаттар бойынша дифференциалы үздіксіз болуы қажет;

3. 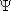- функциясының модулінің квадратының интегралы болу керек және бұл интеграл шекті болу керек.

Микроәлемде өтетін көптеген физикалық құбылыстарды қарастырғанда, мысалы атомдағы электронның күйін зерттегенде уақытқа тәуелсіз Шредингер теңдеуін қарастыру қажет болады. Ол үшін Шредингер жалпы теңдеуінен уақытты қысқарта отырып, Шредингердің стационар теңдеуі алынады.

Шредингер теңдеуіндегі пси функциясының шешімін келесі түрде іздейік: ,

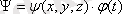мұндағы: 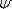айнымалысы координаталардың, 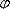- уақыттың функциясы болып табылады. Айнымалыларды бөле отырып Шредингердің стационар теңдеуі алынады

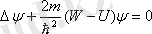Шредингер теңдеуін қанағаттандыратын 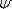функциясын осы теңдеудің меншікті функциясы деп атайды, ал осы теңдеуді қанағаттандыратын толық энергияның мәнін меншікті мән деп атайды.

30. 3. Еркін электрон қозғалысы

Бөлшектің еркін қозғалысы кезінде оның толық энергиясы кинетикалық энергиясына тең болады. Бұл жағдай үшін Шредингер теңдеуі келесі түрде жазылады:

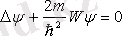Бұл теңдеудің шешімі

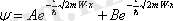
мұндағы: А, В- тұрақты шамалар.

Еркін электронның қозғалысына монохроматты жазық де Бройль толқыны сәйкес келеді.

3. Потенциал “шұңқырдағы” электрон

Бір өлшемді шексіз терең потенциалды шұңқырдағы электронның қозғалысын қарастырайық.

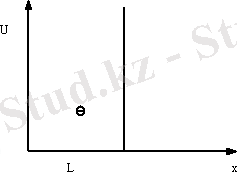
http://sanatez.net/fiz_electronka/htm/5_1.files/image062.gif

Электронның шұңқыр ішіндегі және тыс жердегі потенциалдық энергиясы келесі мәндерді қабылдайды

( ),

( ) .

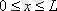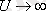Потенциалды өрісте қозғалатын электронның қозғалысы үшін Шредингер теңдеуін қолдана отырып, алатынымыз

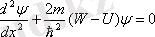
Электронның потенциалды шұңқырдан тыс жерде табылу ықтималдылығы нольге тең. Сол себепті терең потенциалды шұңқырдағы электронның қозғалысын зерттейтін есеп төменде көрсетілген шекті шарттары бар келесі дифферециалдық теңдеуді шешуге келеді

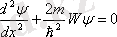мұндағы: 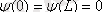толқындық функция үшін шекті шарттар.

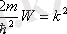белгілей отырып, теңдеудің шешімін келесі түрде жазамыз:

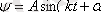
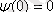шартынан 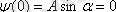және 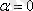екені алынады.

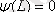шартынан 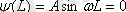және 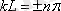( 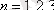) екені алынады.

Жоғарыдағы теңдеулерден -ні қысқарта отырып электронның энергиясының меншікті мәнін табамыз

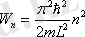мұндағы:

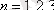
Потенциалдық шұңқырдағы электронның толық энергиясы тек дискретті мәндерді қабылдайды. Кванттық механикада дискреттік мәндерді қабылдайтын шамаларды квантталатын шамалар деп атайды.

Сондай-ақ потенциалды шұңқырдағы электронның меншікті функциясы келесі түрде жазылады:

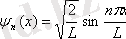30. 5. Гармониялық осцилятор

Квазисерпімді күштің әсерінен бір өлшемді тербеліс жасайтын бөлшекті гармониялық осцилятор деп аталады. Бұл бөлшектің потенциалдық энергиясы келесі формуламен анықталды:

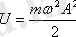
Гармониялық осцилятор үшін Шредингер теңдеуі келесі түрде жазылады:

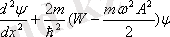
Дифференциалдық теңдеулер теориясынан жоғарыдағы теңдеудің шешімі келесі мәндерінде шекті, бірмәнді және үздіксіз болатыны дәлелденген:

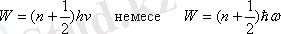мұндағы:

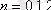
Суретте гармониялық осцилятордың энергетикалық деңгейлерінің схемасы көрсетілген. Ең аз мүмкін энергияның мәні 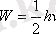Бұл энергияны нольдік энергия деп атайды.

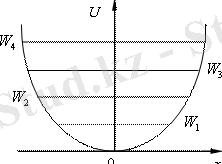
Абсолют ноль Кельвинде гармониялық осциляторлар тепе-теңдік күйінің айналасында нольдік тербеліс жасайды.

Қорытынды

Кванттық механика қазіргі заманғы физиканың негізгі теориясының бірі. Кванттық механика - микробөлшектердің (элементар бөлшектердің, атомдардың, молекулалардың) қозғалыс заңдылықтарын зерттейтін теория.

Кванттық механиканың алғашқы даму тарихын қарастыра отырып, негізгі үш кезеңді ерекше бөліп алуға болады. Бірінші кезең: XIX ғасырдың аяғы - 1912 ж. (алғашқы тәжірибелер және оларды түсіндіру әрекеттері) . Екінші кезең: 1913 - 1922 ж. ж. (Бордың кванттық теориясы) . Үшінші кезең: 1923 - 1927 ж. ж. (кванттық механиканың пайда болуы және дамуы) .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.