Ықтималдық теориясының негізгі теоремелері: қосу және көбейту теоремелері, шартты ықтималдық, толық ықтималдық формуласы және Байес теоремасы


ЖОСПАР
1. Ықтималдықтың негізгі теоремалары.
2. Қосу және көбейту теоремалары.
3. Толық ықтималдықтын формуласы.
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР
1. Ықтималдықтың негізгі теоремалары.
Теорема. Үйлесімсіз екі А және В оқиғалар қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең, яғни
Р(А+В) =Р(А) +Р(В) . (1)
Дәлелдеуі. Дәлелдеу үшін (1) теңдіктегі үш ықтималдықты есептеп, олардың мәндерін қайтадан осы теңдікке қойып, дұрыстығына көз жеткізу жеткілікті. Шынында да, тең мүмкіндікті үйлесімсіз оқиғалардың толық тобын құрайтын элементар оқиғалар саны n болсын. Олардың ішінде А оқиғасына қолайлысы
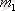 бұлар В үшін қолайсыз, В оқиғасына қолайлысы
бұлар В үшін қолайсыз, В оқиғасына қолайлысы
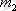 бұлар А үшін қолайсыз болсын. Демек, Р(А) =
бұлар А үшін қолайсыз болсын. Демек, Р(А) =
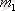 /n, P(B) =
/n, P(B) =
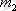 /n. А+В оқиғасына қолайлысы -
/n. А+В оқиғасына қолайлысы -
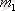 +
+
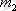 , өйткені А мен В үйлесімсіз. Сондықтан бір сынауда екеуіне де бірдей қолайлы элементар оқиғалар болмайды. Демек, Р(А+В) =(
, өйткені А мен В үйлесімсіз. Сондықтан бір сынауда екеуіне де бірдей қолайлы элементар оқиғалар болмайды. Демек, Р(А+В) =(
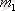 +
+
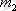 ) 1/ n=
) 1/ n=
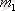 /n +
/n +
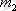 /n=Р(А) +Р(В) . Осымен теорема дәлелденді.
/n=Р(А) +Р(В) . Осымен теорема дәлелденді.
Бұл қасиет оқиғалар саны 2-ден артық (яғни саны n) болғанда орын алады.
Теорема. Егер A 1, A 2, …, A n қос-қостан үйлесімсіз оқиғалар болса, онда бұлардың қосындысының ықтималдығы әрқайсысының ықтималдықтарының қосындысына тең болады, яғни
Р(A 1 +А 2 + . . . +А n ) =Р(А 1 ) +Р(А 2 ) + . . . +Р(А n ) . (2)
Дәлелдеуі. Мұны толық математикалық индукция әдісімен дәлелдейік. n=2 болғанда теореманың дұрыстығы өткен теоремада дәлелденді. Бұл теорема n=k үйлесімсіз A 1, A 2, …, A k оқиғалары үшін дұрыс, яғни Р(A 1 +А 2 + . . . +А k ) =Р(А 1 ) +Р(А 2 ) + . . . +Р(А k ) болсын. Енді n=k+1 болғанда да теорема дұрыс болатынын дәлелдейміз. Берілгені бойынша A 1 +А 2 + . . . +А k, А k+1 оқиғалары қос-қостан үйлесімсіз, олай болса, (A 1 +А 2 + . . . +А k ) мен А k+1 оқиғалары да үйлесімсіз. Демек, бұл екі оқиғаға (1) формуласын пайдаланамыз, сонда
Р(A 1 +А 2 + . . . +А k +А k+1 ) =Р((A 1 +А 2 + . . . +А k ) +А k+1 ) =
(A 1 +А 2 + . . . +А k ) +Р (А k+1 )
болады. бұдан теореманың n=k+1 үшін де дұрыс екенін көреміз. Олай болса, теорема n-ның кез келген мәні үшін де дұрыс.
Ықтималдықтарды көбейту теоремасы.
Тәуелсіз және тәуелді оқиғалар. Ықтималдықтар теориясында оқиғаларды элементар оқиғаларға бөліп қана қоймай, оқиғалардың өзара тәуелділігі мен тәуелсіздігінің де жігін айырып қарастырады.
Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе, онда оларды тәуелсіз оқиғалар деп атайды.
1-мысал. Қобдишада 10 шар бар, оның төртеуі ақ, алтауы қызыл. Қобдишадан кез келген бір шарды алып, түсін белгілегеннен соң екіншісін алады. Бірінші алынған шар қызыл түсті болғанда екінші рет алынған шардың ақ түсті болу ықтималдығын анықтау керек.
Шешуі. Бұл мысалдың шешуі қобдишадан алынған бірінші шар түсі белгіленген соң екінші шарды алу алдында ол шар қайта қобдишаға салыну (бірінші тәсіл), әлде қайта салынбауына (екінші тәсіл) байланысты ықтималдық мәні түрліше болады.
Бірінші тәсіл. Қобдишадан бірінші рет алынған шар түсі қызыл болуы В оқиғасы болсын, онда
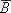 оқиғасы қобдишадан алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады. Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын, онда
оқиғасы қобдишадан алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады. Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын, онда
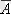 оқиғасы екінші ретте қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет алынғанда да қобдишадағы шарлар саны бастапқыдай болады. Сондықтан А оқиғасының ықтималдығы оған дейін қабдишадан қызыл шар (В оқиғасы) шығуына байланысты емес, өзгермейді және ол 0, 4-ке тең. Бұдан В оқиғасының пайда болуының А оқиғасының ықтималдығына әсері болмайтынын байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
оқиғасы екінші ретте қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет алынғанда да қобдишадағы шарлар саны бастапқыдай болады. Сондықтан А оқиғасының ықтималдығы оған дейін қабдишадан қызыл шар (В оқиғасы) шығуына байланысты емес, өзгермейді және ол 0, 4-ке тең. Бұдан В оқиғасының пайда болуының А оқиғасының ықтималдығына әсері болмайтынын байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Екінші тәсіл. Тәжірибе шарты 1 - мысалдағыдай, бірақ бірінші рет алынған шар қобдишаға қайта салынбайды. Бұл жағдайда екінші ретте А оқиғасының пайда болу ықтималдығы оның алдында қызыл шар (В), не ақ шар (
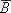 оқиғасы) шығуына байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші сынауда
оқиғасы) шығуына байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші сынауда
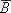 оқиғасы пайда болса (ақ шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы) ықтималдығы 3/9=1/3-ке тең. Осы сияқты, егер бірінші сынауда қызыл шар (
оқиғасы пайда болса (ақ шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы) ықтималдығы 3/9=1/3-ке тең. Осы сияқты, егер бірінші сынауда қызыл шар (
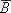 оқиғасы) не ақ шар (
оқиғасы) не ақ шар (
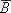 оқиғасы) шықты десек, онда екінші сынауда қызыл шар (
оқиғасы) шықты десек, онда екінші сынауда қызыл шар (
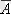 оқиғасы) пайда болу ықтималдығы сәйкес 5/9 және 2/3 сандарына тең. Екінші сөзбен айтқанда А және В оқиғалары- тәуелді оқиғалар, өйткені бірінші жолы В оқиғасының пайда болуы келесі жолы А оқиғасының пайда болу ықтималдығын өзгертіп отыр.
оқиғасы) пайда болу ықтималдығы сәйкес 5/9 және 2/3 сандарына тең. Екінші сөзбен айтқанда А және В оқиғалары- тәуелді оқиғалар, өйткені бірінші жолы В оқиғасының пайда болуы келесі жолы А оқиғасының пайда болу ықтималдығын өзгертіп отыр.
2. Қосу және көбейту теоремалары.
Шартты ықтималдық. 1-мысалда А оқиғасының ықтималдығын есептегенде комплексті шарттан басқа В оқиғасының пайда болу, не пайда болмауы әсер етіп, А оқиғасының ықтималдығын өзгертіп отырды. Мұндай ықтималдықты шартты ықтималдық деп атайды. Шартты ықтималдықты былай белгілейді: Р(А/В) немесе Р В (А) . Бұл былай оқылады: В оқиғасы орындалғанда А оқиғасының пайда болу ықтималдығы. Жоғарыда айтылғандарға сұйене отырып, А және В оқиғаларының тәуелсіздігін Р(А/В) = Р(А), (Р В (А) = Р(А) ) тұрінде жазуға болады. Бұл жағдайда 1-мысалдан
Р(А) =Р(А/В) =0, 4, Р(А) =Р(А/
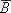 ) =0, 4
) =0, 4
сондай-ақ
Р(
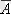 ) =Р(
) =Р(
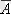 /В) =0, 6, Р(
/В) =0, 6, Р(
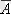 ) =Р(
) =Р(
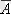 /
/
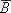 ) =0, 6
) =0, 6
Егер А және В оқиғалары бір-біріне тәуелді болса, онда сол мысалдан Р(А) =Р(А/В), Р(А/В) =4/9, Р(А/
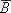 ) =1/3; сондай-ақ
) =1/3; сондай-ақ
Р(
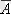 /В) =5/9, Р(
/В) =5/9, Р(
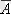 /В) =2/3.
/В) =2/3.
Шартты ықтималдықтың қасиеттері, шартсыз ықтималдық қасиеттеріндей.
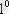 . Шартты ықтималдық мәні де, шартсыз ықтималдық мәні сияқты, нөл мен бір аралығында болады, яғни
. Шартты ықтималдық мәні де, шартсыз ықтималдық мәні сияқты, нөл мен бір аралығында болады, яғни
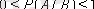
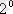 . P(U/B) =1.
. P(U/B) =1.
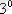 .
.

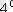 Егер
Егер
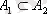 болса, онда
болса, онда
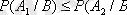
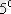 Егер
Егер
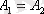 болса, онда
болса, онда
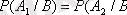
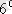 Егер
Егер
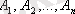 оқиғалары қос-қостан ұйлесімсіз, яғни
оқиғалары қос-қостан ұйлесімсіз, яғни
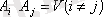 және
және
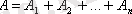 болса, онда
болса, онда


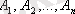 қос-қостан ұйлесімсіз болса және олар оқиғалардың толық жұйесін құраса, яғни
қос-қостан ұйлесімсіз болса және олар оқиғалардың толық жұйесін құраса, яғни
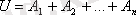 болса, онда
болса, онда
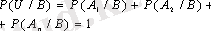
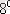 А мен
А мен
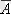 қарама-қарсы оқиғалар болса, онда
қарама-қарсы оқиғалар болса, онда
Р(А/В) =1-Р(
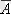 /В) .
/В) .
Ықтималдықтарды көбейту теоремасы. Бұл теорема тәуелді немесе тәуелсіз екі және бірнеше оқиғалардың бірден пайда болу ықтималдығын есептеуге мұмкіндік береді.
Теорема. Екі тәуелді оқиға көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен сол оқиға пайда болғандағы екінші оқиғаның шартты ықтималдығының көбейтіндісіне тең:
Р(АВ) =Р(А) Р(В/А) =Р(В) Р(А/В) .
3. Толық ықтималдықтын формуласы.
Күрделі оқиғалар ықтималдығын есептегенде ықтималдықтарды қосу, көбейту теоремаларын қатарынан жиі қолдануға тура келеді. Мұндай оқиғалардың ықтималдығын есептеуге арналған формуланы қорытудан бұрын мынадай мәселеге тоқтап өтейік.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz