Сызықтық программалаудың теориясы, қасиеттері және симплекстік әдіспен шешу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 57 бет
Таңдаулыға:
Жанай Гаухар 04401а
Сызықтық программалаудың есептері
Мазмұны
Кіріспе
Математикалық программалау өз алдына экстремальдық есептерді оқыту мен оларды шешу әдістерін қарастыру математиканың бір бөлімі болып табылады.
Экстемальдық есептердің жалпы түрдегі математикалық қойылымы анықтамадағы
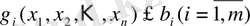 шартының
шартының
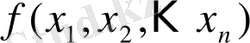 бүтін функциясынан тұрады, мұндағы
бүтін функциясынан тұрады, мұндағы
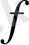 және
және
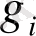 - берілген функция, ал
- берілген функция, ал
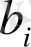 - кейбір нақты сан.
- кейбір нақты сан.
 және
және
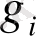 функцияларының қасиеттеріне байланысты математикалық программалауды белгілі бір есептердің классын оқыту мен оларды шешу әдістерімен шұғылданатын дербес пән ретінде қарастыруға болады.
функцияларының қасиеттеріне байланысты математикалық программалауды белгілі бір есептердің классын оқыту мен оларды шешу әдістерімен шұғылданатын дербес пән ретінде қарастыруға болады.
Ең алдымен математикалық программалаудың есептері сызықтық және сызықтық емес программалау есептері болып бөлінеді. Бұл жағдайда барлық
 және
және
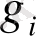 функциялары сызықтық болса, онда тиісті есеп те сызықтық программалудың есептері болып табылады.
функциялары сызықтық болса, онда тиісті есеп те сызықтық программалудың есептері болып табылады.
Математикалық программалаудың көбіне оқылатын бөлімі сызықтық программалау болып табылады. Сызықтық программалаудың есептерін шешу үшін көптеген тиімді әдістер, алгоритмдер және программалар жасалған.
Ең алғаш сызықтық программалаудың есептерінәйгілі Кеңес одағының математигі Контеровичпен тұжырымдалған, және бұл жұмысы үшін экономика бойынша Нобельдік сыйлығы тағайындалды.
Дипломдық жұмыс кіріспеден, үш параграфтан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Бірінші параграфта сызықтық программалаудың жалпы және негізгі есептеріне бірнеше мысалдар келтіру арқылы қарастырылған.
Екінші параграфта сызықтық программалаудың негізгі есебінің қасиеттеріне тоқталып өтілген.
Үшінші параграфта сызықтық программалаудың есептерін симплексті әдіспен шешуге байланысты мысалдар келтіріліп және олардың шешу жолдары көрсетілген.
Осы сызықтық программалаудың есептеріне қатысты көптеген мысалдар қарастырылып, олардың шығарылу әдістері зерттелген.
Дипломдық жұмыстың барлық теориялық материалдары мысалдар келтіру арқылы бекітіліп және әр түрлі әдістер қолдана отырып шешуге бағытталған.
Өзектілігі:
- Қазіргі заманғы ғылымның «Сызықтық программалау»-ға деген үлкен қызығушылықтың болуы;
- Сызықтық программалаудың есептеріне байланысты мәселелерді теориялық және практикалық маңыздылығы жағынан қарау.
Дипломдық жұмыстың мақсаты. Сызықтық программалаудың есептерін шешу әдістерін зерттеу.
Зерттеу объектісі. Сызықтық программалаудың есептері.
Зерттеу пәні. Сызықтық программалаудың есептерін шешу.
Зерттеу жұмысының міндеттері:
- ғылыми және әдістемелік материалдарды жинақтап талдау;
- сызықтық программалаудың есептерінің шешімдерін зерттеу;
- сызықтық программалаудың есептерін симплексті әдісті қолдану арқылы шешуді зерттеу.
1 Сызықтық программалаудың жалпы және негізгі есептері
Ең алдымен сызықтық программалау есептеріне бірнеше мысалдар қарастырайық.
Мысал 1.
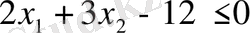
теңсіздігімен анықталатын жарты жазықтықты табыңыз.
Шешімі
. теңсіздікті тура теңдікке алмастыру арқылы
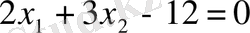 немесе
немесе
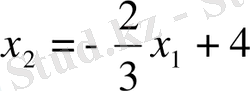 түзуінің теңдеуін аламыз (1 сурет) . Берілген теңсіздікті
түзуінің теңдеуін аламыз (1 сурет) . Берілген теңсіздікті
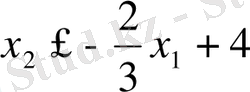 түріне келтіріп аламыз. Сәйкесінше, ізделініп отқан жарты жазықтық
түріне келтіріп аламыз. Сәйкесінше, ізделініп отқан жарты жазықтық
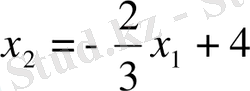 түзуінен төмен орналасқан.
түзуінен төмен орналасқан.
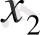
1 сурет
Мысал 2. Қандай жазықтықты
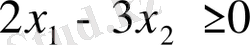
теңсіздігі анықтайды?
Шешімі
. теңсіздікті тура теңдікке алмастыру арқылы, координта басынан өтетін
 немесе
немесе
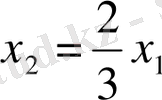 түзуінің теңдеуін аламыз. Ізделініп отырған жарты жазықтық
түзуінің теңдеуін аламыз. Ізделініп отырған жарты жазықтық
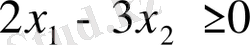 теңсіздігінен
теңсіздігінен
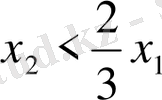 шығады және ол
шығады және ол
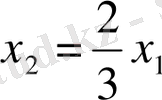 түзуінен төмен орналасқан (2 сурет) .
түзуінен төмен орналасқан (2 сурет) .
2 сурет
Мысал 3.
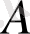 ,
,
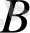 және
және
 бұйымдарының үш түрін дайындау үшін токарлық, фрезерлік, дәнекерлейтін және тегістейтін (өңдейтін) құралдар пайдаланылады. Құрал-жабдықтың әрбір типінің бір бұйымды өңдеуге шығындайтын уақыты 1 кестеде көрсетілген. Онда пайдаланылатын құрал-жабдықтың әрбір типінің жұмыс уақытының жалпы қоры, сондай-ақ, әрбір түрдің бір бұйымын жасаудан шығатын пайда көрсетілген. Олардың іске асырылуынан максимальді пайда болуы үшін кәсіпорынға қанша бұйым және қай түрінен дайындау (жасап шығару) қажеттігін анықтау талап етіледі. Тапсырманың математикалық моделін құрастыру керек.
бұйымдарының үш түрін дайындау үшін токарлық, фрезерлік, дәнекерлейтін және тегістейтін (өңдейтін) құралдар пайдаланылады. Құрал-жабдықтың әрбір типінің бір бұйымды өңдеуге шығындайтын уақыты 1 кестеде көрсетілген. Онда пайдаланылатын құрал-жабдықтың әрбір типінің жұмыс уақытының жалпы қоры, сондай-ақ, әрбір түрдің бір бұйымын жасаудан шығатын пайда көрсетілген. Олардың іске асырылуынан максимальді пайда болуы үшін кәсіпорынға қанша бұйым және қай түрінен дайындау (жасап шығару) қажеттігін анықтау талап етіледі. Тапсырманың математикалық моделін құрастыру керек.
1кесте
Құрал-жабдық
типі - металл
Түрдің бір бұйымын
өңдеуге шығындайтын уақыты (станок)
Фрезерлік - темір
Токарлық - аллюминий
Дәнекерлейтін - мыс
Тегістейтін - алтын
2
1
7
4
4
8
4
6
5
6
5
7
120
280
240
360
Шешімі. Бұйымның
 түрінен
түрінен
 бірлік,
бірлік,
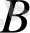 түрінен
түрінен
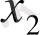 бірлік және
бірлік және
 түрінен
түрінен
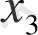 бірлік дайындалады делік. Онда сондай бұйым санының өндірісі үшін фрезерлік құрал-жабдықтың
бірлік дайындалады делік. Онда сондай бұйым санының өндірісі үшін фрезерлік құрал-жабдықтың
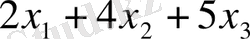 станок-сағат уақыты қажет болады.
станок-сағат уақыты қажет болады.
Аталмыш типтегі станоктардың жұмыс уақытының жалпы қоры 120-дан артық болғандықтан, теңсіздік орындалуы тиіс
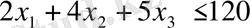 .
.
Токарлық, дәнекерлейтін және тегістейтін құрал-жабдықтардың қатысты мүмкін қолданылуын осылай пайымдау келесі теңсіздіктерге алып келеді:

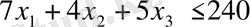

Мұнымен қоса дайындалатын бұйымдардың саны теріс бола алмайтындықтан
 . (1)
. (1)
Әрі қарай бұйымның
 түрінен
түрінен
 бірлік,
бірлік,
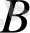 түрінен
түрінен
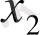 бірлік,
бірлік,
 түрінен
түрінен
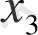 бірлік дайындалатын болса, онда оларды іске асырудан түсетін пайда
бірлік дайындалатын болса, онда оларды іске асырудан түсетін пайда
 құрайды.
құрайды.
Осылайша, келесі математикалық есепке келеміз: үш
 белгісізбен төрт сызықтық теңсіздіктің жүйесі
белгісізбен төрт сызықтық теңсіздіктің жүйесі
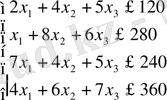 (2)
(2)
және осы айнымалы шамаға қатысты сызықтық функция берілген
 , (3)
, (3)
теңсіздік жүйесінің (2) барлық теріс емес шешімдері арасынан функция (3) максимальді мәнге ие болатындайды табу талап етіледі. Мұны қалай жасау керектігі алдағы уақытта көрсетіледі.
Теңсіздік жүйесімен (2) және айнымалылардың (1) теріс еместік шартымен бірге максимум анықтау керек болатын сызықтық функция (3) бастапқы есептің математикалық моделін қалыптастырады.
Функция (3) сызықтық, ал жүйе тек сызықтық теңсіздіктен тұратын болғандықтан, (1) -(3) есебі сызықтық программалау есбеі болып табылады.
Мысал 4. Қалалық сүт зауытының өнімдері - бөтелкелерге бөлшектелген сүт, айран және қаймақ. 1 т сүт, айран және қаймақ өндірісіне сәйкесінше 1010, 1010 және 9460 кг сүт талап етіледі. Мұнымен қоса, 1 т сүт пен айранды бөліп құю кезіндегі жұмыс уақытының шығыны 0, 18 және 0, 19 машина уақытын құрайды. 1 т қаймақты бөлшектеп құюға 3, 25 сағ бойы арнайы автоматтар жұмыс жасайды. Қаймағы алынбаған сүт өнімдерінің өндірісі үшін зауыт барлығы 136000 кг сүт пайдалана алады. Негізгі құрал-жабдықтар 21, 4 машина с бойы, ал қаймақты бөлшектейтін автоматтар 16, 25 сағ. бойы жұмыс істейді. 1 т сүт, айран және қаймақ өндірісіен келетін пайда сәйкесінше 30, 22 және 136 теңгеге тең. Зауыт күн сайын бөтелкелерге бөлшектеліп құйылған 100 т сүттен кем шығармауы тиіс. Басқа өнім өндірісіне ешқандай шектеу жоқ.
Өнімді шығарғаннан түсетін пайда максимальды болуы үшін зауыт күн сайын қандай өнімді және қандай мөлшерде дайындауы қажеттігін анықтау талап етіледі. Есептің математикалық моделін құрамыз.
Шешімі. Сүт зауыты күн сайын
 тонна сүт,
тонна сүт,
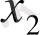 тонна айран және
тонна айран және
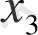 тонна өндіріп шығарады делік. Онда оғаны осы өнімді дайындауы үшін
тонна өндіріп шығарады делік. Онда оғаны осы өнімді дайындауы үшін
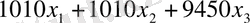 тонна сүт қажет.
тонна сүт қажет.
Зауыт күн сайын 136 000 т артық емес сүт пайдалана алатындықтан, келесі теңсіздік орындалуы тиіс
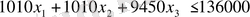
Қаймағы алынбаған сүт өнімдерінің бөліп құю және қаймақты бөлшектеп құятын автоматтар линиясын пайдалану ықтималдығына қатысты жүргізілген осыған ұқсас пайымдаулар келесі теңсіздікті жазуға мүмкіндік береді:

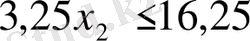
Күн сайын 100 т кем емес сүт өндірілуі керек болғандықтан,
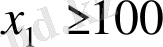 . Одан әрі
. Одан әрі
 және
және
 айнымалылыары өзінің экономикалық мәніне қарай тек теріс:
айнымалылыары өзінің экономикалық мәніне қарай тек теріс:
 ,
,
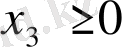 мәнді мәнді ғана қабылдай алады.
мәнді мәнді ғана қабылдай алады.
 тонна сүт,
тонна сүт,
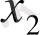 тонна айран және
тонна айран және
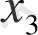 тонна қаймақты өндіргеннен түсетін жалпы пайда
тонна қаймақты өндіргеннен түсетін жалпы пайда
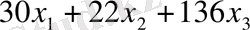 теңгеге тең. Осылайша, келесі математикалық есепке келеміз:
теңгеге тең. Осылайша, келесі математикалық есепке келеміз:
 (4)
(4)
 ,
,
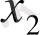 ,
,
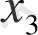 белгісізбен төрт сызықтық теңсіздіктің жүйесі және осы айнымалыларға қатысты сызықтық функция берілген
белгісізбен төрт сызықтық теңсіздіктің жүйесі және осы айнымалыларға қатысты сызықтық функция берілген
 , (5)
, (5)
теңсіздік жүйесінің барлық теріс шешімдерінің арасынан (4) функция (5) максималды мәнге ие болатындайды табу талап етіледі. Жүйе (4) сызықтық теңсіздіктердің жиынтығынан тұрып, функция (5) сызықтық болғандықтан бастапқы есеп сызықтық программалаудың есебі болып табылады.
Мысал 5.
Тігін фабрикасындағы тігін бұйымдарының қажетті детальдерін дайындау үшін мата бірнеше тәсілмен пішілуі мүмкін.
 нұсқасында матаның
нұсқасында матаның
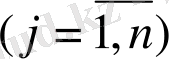 100 м
2
пішуінен
100 м
2
пішуінен
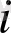 түрінің
түрінің
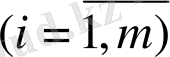
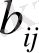 деталі әзірленеді, ал пішудің аталмыш нұсқасындағы қалдықтардың мөлшері
деталі әзірленеді, ал пішудің аталмыш нұсқасындағы қалдықтардың мөлшері
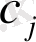 м
2
-қа тең болсын.
м
2
-қа тең болсын.
 түрінің детальдарынан
түрінің детальдарынан
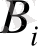 дана әзірлеу керектігін біліп, минимальді жалпы қалдық қалған кезде әрбір түрінен қажетті детал саны алынатындай матаны пішу қажет етіледі. Есептің математикалық моделін құрастырайық.
дана әзірлеу керектігін біліп, минимальді жалпы қалдық қалған кезде әрбір түрінен қажетті детал саны алынатындай матаны пішу қажет етіледі. Есептің математикалық моделін құрастырайық.
Шешімі.
 нұсқасы бойынша м
2
матаның
нұсқасы бойынша м
2
матаның
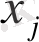 жүзіншісі қиылады деп болжалық. 100 м
2
матаны пішу кезінде
жүзіншісі қиылады деп болжалық. 100 м
2
матаны пішу кезінде
 нұсқасы бойынша
нұсқасы бойынша
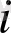 түрінің
түрінің
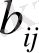 деталдары алынатындықтан, пайдаланылған мата пішінінің барлық нұсқалары бойынша
деталдары алынатындықтан, пайдаланылған мата пішінінің барлық нұсқалары бойынша
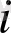 түрінің
түрінің
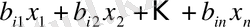
деталы алынады. Аталмыш түрдің
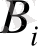 деталы әзірленуі тиіс болғандықтан
деталы әзірленуі тиіс болғандықтан

Мата пішіндерінің барлық нұсқасы бойынша қалдықтардың жалпы мөлшері
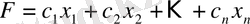
құрайды.
Осылайша, келесі математикалық есепке келеміз
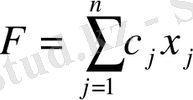 (6)
(6)
функциясының оның айнымалылары
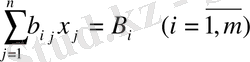 (7)
(7)
теңсіздігі жүйесін қанағаттандыратын шартында және
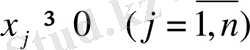 терістік шартында минимумын табу.
терістік шартында минимумын табу.
Тұжырымдалған есеп функция (6) сызықтық, ал жүйе (7) тек сызықтық теңдікті ұстағандықтан сызықтық программалаудың есебі болып табылады.
Жоғарыда сызықтық программалау мысалдары қарастырылды. Осы есептердің барлығында айнымалылары теріс мәнге ие болып, сызықтық теңеулердің немесе сызықтық теңсіздіктердің кейбір жүйесін немесе сызықтық теңсіздіктер секілді сызықтық теңеулерден де тұратын жүйені қанағаттандырады. Осы есептердің әрқайсысы сызықтық программалау жалпы есебінің жеке жағдайы болып табылады.
Анықтама 1. Сызықтық программалаудың жалпы есебі деп
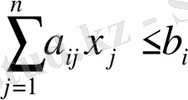
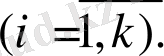 (8)
(8)

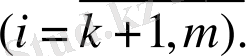 (9)
(9)
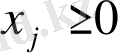
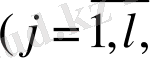
 (10)
(10)
шартындағы
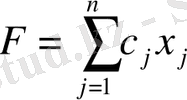 (11)
(11)
функциясының максимальді мәнінің анықтамасынан тұратын есепті айтады. Мұндағы
 ,
,
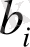 ,
,
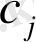 - берілген тұрақты шамалар және
- берілген тұрақты шамалар және
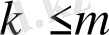 .
.
Анықтама 2. Функция (11) есептің (8) -(11) мақсатты функциясы деп (немесе сызықтық формасы), ал шарт (8) -(10) - берілген есептің шектеулері деп аталады.
Анықтама 3.
Сызықтық программалаудың стандартты (немесе симметриялық) есебі деп
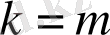 және
және
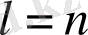 болатын (8) және (10) шарттарын орындау кезіндегі (11) функцияның максимальді мәнінің анықтамасында тұратын есепті айтады.
болатын (8) және (10) шарттарын орындау кезіндегі (11) функцияның максимальді мәнінің анықтамасында тұратын есепті айтады.
Анықтама 4.
Сызықтық программалаудың каноникалық (немесе негізгі) есебі деп
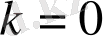 және
және
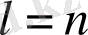 болатын (9) және (10) шарттарын орындау кезіндегі (11) функцияның максимальді мәнінің анықтамасынан тұратын есепті айтады.
болатын (9) және (10) шарттарын орындау кезіндегі (11) функцияның максимальді мәнінің анықтамасынан тұратын есепті айтады.
Анықтама 5.
(8) - (10) есептерінің шектеулерін қанағаттандыратын
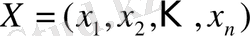 сандарының жиынтығы шектеулі шешім (немесе жоспар) деп аталады.
сандарының жиынтығы шектеулі шешім (немесе жоспар) деп аталады.
Анықтама 6.
(11)
есептің мақсатты функциясы өзінің максимальді (минимальді) мәніне ие болатын
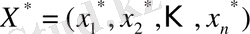 жоспары оңтайлы деп аталады.
жоспары оңтайлы деп аталады.
Мақсатты функцияның (11) мәнін
 жоспарында
жоспарында
 арқылы белгілейміз
.
Ендеше егер кез келген
арқылы белгілейміз
.
Ендеше егер кез келген
 үшін
үшін
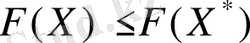 [сәйкесінше
[сәйкесінше
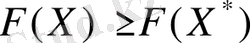 теңсіздігі орындалса
теңсіздігі орындалса
 - есептің оңтайлы жоспары.
- есептің оңтайлы жоспары.
Сызықтық программалау есебінің жоғарыда көрсетілген үш формасы олардың әрқайсысы күрделі емес өзгерістердің көмегімен басқа есептің формасына көшіріп жазылатын жағдайда эквиваленттер болып табылады. Бұл егер көрсетілген есептердің біреуінің шешімін табу тәсілі бар болса, онда сол арқылы үш есептің кез келгенінің оңтайлы жоспары анықталуы мүмкін.
Сызықтық программалау есебі жазбасының бір формасынан басқасына өту үшін жалпы жағдайда біріншіден функция минимизациясының есебін максимизация есебіне қысқарта білу керек, екіншіден теңсіздік шектеуінен теңдік шектеуіне және керісінше өтіп, үшіншіден терістік шартына бағынбайтын айнымалыларды алмастыра білу керек.
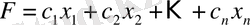 функциясының минимумын табу талап етілген жағдайда
функциясының минимумын табу талап етілген жағдайда
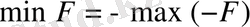 болғандықтан
болғандықтан
 функциясының максимумын табуға көшуге болады.
функциясының максимумын табуға көшуге болады.
Сызықтық программалаудың бастапқы есебінің «
 » түріндегі шектеу-теңсіздігі оның сол бөлігіне қосымша теріс айнымалыны қосып шектеу-теңсіздігіне өзгертуге болады, «
» түріндегі шектеу-теңсіздігі оның сол бөлігіне қосымша теріс айнымалыны қосып шектеу-теңсіздігіне өзгертуге болады, «
 » түріндегі шектеу-теңсіздігін оның сол бөлігінен қосымша теріс айнымалыны азайту арқылы шектеу-теңдікке айналдыруға болады. Осылайша
» түріндегі шектеу-теңсіздігін оның сол бөлігінен қосымша теріс айнымалыны азайту арқылы шектеу-теңдікке айналдыруға болады. Осылайша
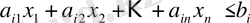
шектеу-теңсіздігі
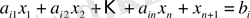
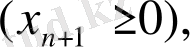 (12)
(12)
шектеу-теңдігіне (теңдеуіне) өзгереді, ал
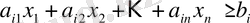
шектеу-теңсіздігі
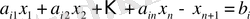
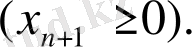 (13)
(13)
шектеу-теңдігіне айналады.
Сонымен қатар шектеу жүйесінің әрбір теңдеуін
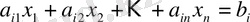
теңсіздік түрінде жазуға болады:
 (14)
(14)
Енгізілетін қосымша теріс айнымалылардың саны шектеу-теңсіздігінен шектеу-теңдігіне өзгеру кезінде өзгерілетін теңсіздіктер санына тең.
Енгізілетін қосымша айнымалылар толықтай анықталған экономикалық мағынаға ие. Мысалы, егер сызықтық программалаудың шектеулерінде өндірістік ресурстардың шығыны мен қолда бары көрінсе, онда негізгі формада жазылған есеп жоспарындағы қосымша айнымалының сандық мәні пайдаланылмаған тиісті ресурстың көлеміне тең.
Егер
 айнымалы терістік шартына бағынбаған болса, онда оны
айнымалы терістік шартына бағынбаған болса, онда оны
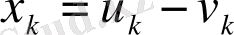 қабылдап
қабылдап
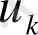 және
және
 екі теріс емес айнымалыларға ауыстырған жөн.
екі теріс емес айнымалыларға ауыстырған жөн.
Мысал 6 .
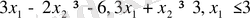 шектелген
шектелген
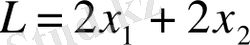 сызықтық формасын кеңейту.
сызықтық формасын кеңейту.
Шешімі
. Теңсіздіктің таңбасын қатаң теңдікке алмастырып,
 түзулерінің теңдеуі арқылы мәндер облысын құрамыз. (сурет 3) .
түзулерінің теңдеуі арқылы мәндер облысын құрамыз. (сурет 3) .
Теңсіздіктің мәндер облысы
 үшбұрышы болады.
үшбұрышы болады.
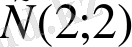 векторын құрайық.
векторын құрайық.
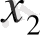
3 сурет
Мысал 7. Сызықтық программалау есебінің негізгі формасында келесі есепті жазу:
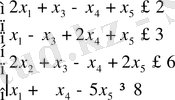
 .
.
шарты кезіндегі
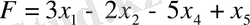 функциясының максимумын табу.
функциясының максимумын табу.
Шешімі.
Берілген есепте функцияның максимумын табу керек, ал шектеу жүйесі төрт теңсіздіктен тұрады. Сондықтан оны негізгі есеп формасында жазу үшін шектеу-теңсіздігінен шектеу-теңдігіне өту керек. Есептің шектеу жүйесіне кіретін теңсіздіктер саны төртке тең болғандықтан бұл көшу төрт қосымша теріс емес айнымалыларды енгізу арқылы жүзеге асырылуы мүмкін. Мұнымен қоса «
 » түріндегі теңсіздіктердің әрқайсысының сол бөліктеріне сәйкесті қосымша айнымалы қосылады, ал «
» түріндегі теңсіздіктердің әрқайсысының сол бөліктеріне сәйкесті қосымша айнымалы қосылады, ал «
 » түріндегі теңсіздіктің әрқайсысының сол бөлігінен алынады. Шектеу нәтижесінде келесі теңдеу түрі алынады:
» түріндегі теңсіздіктің әрқайсысының сол бөлігінен алынады. Шектеу нәтижесінде келесі теңдеу түрі алынады:
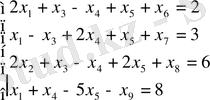

Ендеше, аталмыш есеп негізгі есеп формасында былайша жазылуы мүмкін:
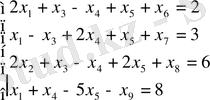
шартындағы
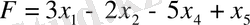 функциясын максимализациялау.
функциясын максимализациялау.
Мысал 8.

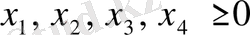
шартындағы
 функциясының минимизациясынан тұратын есепті сызықтық программалау негізгі есебінің формасында жазу.
функциясының минимизациясынан тұратын есепті сызықтық программалау негізгі есебінің формасында жазу.
Шешімі. Берілген есепте мақсатты функцияның минимусын табу талап етіледі, ал шектеу жүйесі үш теңсіздіктен тұрады. Ендеше, оны негізгі есеп формасында жазып алу үшін
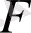 функциясының минимумын табудың орнына шектеу-теңсіздігінін әрқайсысының сол бөлігіне қосымша теріс емес айнымалының «
функциясының минимумын табудың орнына шектеу-теңсіздігінін әрқайсысының сол бөлігіне қосымша теріс емес айнымалының «
 » түрін қосу арқылы бастапқы есептің шектеуінен және «
» түрін қосу арқылы бастапқы есептің шектеуінен және «
 » түріндегі шектеу-теңсіздігінің әрқайсысының сол бөлігінен қосымша айнымалыларды азайту арқылы алынған шектеулер кезіндегі
» түріндегі шектеу-теңсіздігінің әрқайсысының сол бөлігінен қосымша айнымалыларды азайту арқылы алынған шектеулер кезіндегі
 функциясының максимумын табу керек.
функциясының максимумын табу керек.
Ендеше, бастапқы есеп сызықтық программалаудың негізгі есебі формасында былай жазылуы мүмкін:
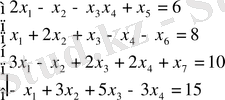
 .
.
шартындағы
 функциясының максимумын табу.
функциясының максимумын табу.
Мысал 9. Сызықтық программалаудың стандартты формасында келесі есепті жазу:
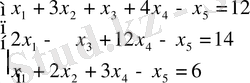
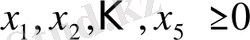 .
.
шартындағы
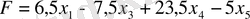 функциясының максимумын табу.
функциясының максимумын табу.
Шешімі. Белгісіздерді жүйелі шығару әдісі арқылы аталмыш есепті келесіге келтіреміз:
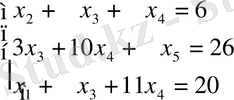
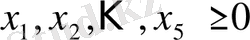 .
.
шартындағы
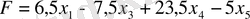 функциясының максимумын табу.
функциясының максимумын табу.
Соңғы есеп
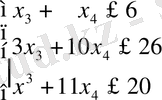
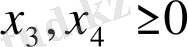 .
.
шартындағы
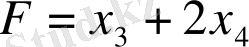 функциясының максимальді мәнін табудан тұратын есепке арналған негізгі формасында жазылған.
функциясының максимальді мәнін табудан тұратын есепке арналған негізгі формасында жазылған.
Есептің мақсатты функциясы
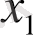 және
және
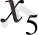 орнына есептің шектеу жүйесінің теңдеулеріне сәйкес олардың мәндерін қою арқылы түрлендірілген.
орнына есептің шектеу жүйесінің теңдеулеріне сәйкес олардың мәндерін қою арқылы түрлендірілген.
2 Сызықтық программалаудың негізгі есебінің қасиеттері
Сызықтық программалаудың негізгі есебін қарастырамыз. § 1-де атап өткендей ол
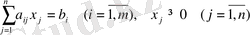 шартындағы
шартындағы
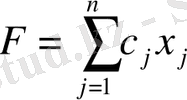 функциясының максимальді анықтамасынан тұрады.
функциясының максимальді анықтамасынан тұрады.
Бұл есепті векторлық формада қайта көшіреміз:
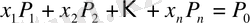 (15)
(15)
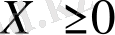 (16)
(16)
шартындағы
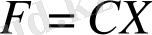 (17)
(17)
функциясының максимумын табу. Мұндағы
 ,
,
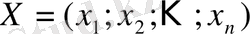
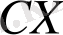 скаляр көбейтінді;
скаляр көбейтінді;
 және
және
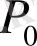 келесі есептің теңдеу жүйесінің белгісіз және бос мүшелеріндегі коэффициенттерден құралған,
келесі есептің теңдеу жүйесінің белгісіз және бос мүшелеріндегі коэффициенттерден құралған,
 - өлшеуіш вектор-бағандар:
- өлшеуіш вектор-бағандар:
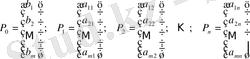 .
.
Анықтама 7.
Егер жіктеуге кіретін
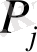 векторларының жүйесі (16)
векторларының жүйесі (16)
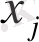 оң коэффициенттерімен сызықтық тәуелсіз болса
оң коэффициенттерімен сызықтық тәуелсіз болса
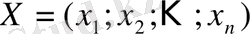 жоспары сызықтық программалаудың негізгі есебінің тірек жоспары деп аталады.
жоспары сызықтық программалаудың негізгі есебінің тірек жоспары деп аталады.
Сөйтіп,
 векторлары
векторлары
 -өлшеуіш болғандықтан, тірек жоспары анықтамасынан оның оң компоненттерінің саны
-өлшеуіш болғандықтан, тірек жоспары анықтамасынан оның оң компоненттерінің саны
 -дан көп бола алмайтыны шығады.
-дан көп бола алмайтыны шығады.
Анықтама 8. Тірек жоспары бірдеу
 оң компоненттерінен тұрса ол өзгешеленбеген деп, ал керісінше жағдайда өзгешеленген деп аталады.
оң компоненттерінен тұрса ол өзгешеленбеген деп, ал керісінше жағдайда өзгешеленген деп аталады.
Сызықтық программалаудың негізгі есебінің (15) - (17) қасиеті дөңес жиындар қасиеттерімен тығыз байланысты.
Анықтама 9.
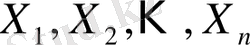 -
-
 евклид кеңістігінің кез келген нүктелері болсын. Осы нүктелердің дөңес сызықтық комбинациясы деп жиынтығы
евклид кеңістігінің кез келген нүктелері болсын. Осы нүктелердің дөңес сызықтық комбинациясы деп жиынтығы
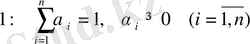 тең,
тең,
 - кез келген теріс саны болатын,
- кез келген теріс саны болатын,
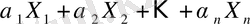 жиынтығы аталады.
жиынтығы аталады.
Анықтама 10. Егер жиынтық өзінің кез келген екі нүктесімен бірге олардың кез келген дөңес сызықтық комбинациясынан тұрса онда ол жиынтық дөңес деп аталады.
Анықтама 11. Дөңес жиынтықтың
 нүктесі егер аталмыш жиынтықтың қандай да бір екі әр алуан нүктесінің дөңес сызықтық комбинациясы түрінде көрсетілмесе онда ол нүтке бұрыштық деп аталады.
нүктесі егер аталмыш жиынтықтың қандай да бір екі әр алуан нүктесінің дөңес сызықтық комбинациясы түрінде көрсетілмесе онда ол нүтке бұрыштық деп аталады.
Теорема 1. Сызықтық программалаудың негізгі есебі жоспарларының жиынтығы (егер ол бос болмаса) дөңес болып табылады.
Анықтама 12. Сызықтық программалаудың негізгі есебі жоспарының бос емес жиынтығы шешімнің көпжағы (көп қырлы дене) деп, ал шешім көп жағының кез келген бұрыштық нүктесі - ұшы деп аталады.
Теорема 2. Егер сызықтық программалаудың негізгі есебінің тиімді жоспары болса, онда есептің мақсатты функциясының максимальді мәні ұштардың бірінде шешім көп қырын қабылдайды. Егер есептің мақсатты функциясының максимальді мәні бір ұштан да көп қабылдаса, онда ол оны осы ұштардың дөңес сызықтық комбинациясы болып табылатын кез келген нүктеде қабылдайды.
Теорема 3.
Егер жіктеудегі (16)
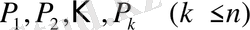 векторлар жүйесі сызықтық тәуелсіз болса және
векторлар жүйесі сызықтық тәуелсіз болса және
 ,
(18)
,
(18)
мұндағы
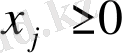 болса, онда
болса, онда
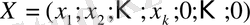 нүктесі шешім көп жақтың (көп қырлы дененің) ұшы болып табылады.
нүктесі шешім көп жақтың (көп қырлы дененің) ұшы болып табылады.
Теорема 4.
Егер
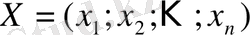 - шешім көпжақтың (көп қырлы дененің) ұшы болса, онда оң
- шешім көпжақтың (көп қырлы дененің) ұшы болса, онда оң
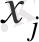 -пен сәйкес келетін
-пен сәйкес келетін
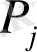 векторлары жіктеуде (16) сызықты тәуелсіз.
векторлары жіктеуде (16) сызықты тәуелсіз.
Тұжырымдалған теоремалар келесі қорытындылар жасауға мүмкіндік береді.
Сызықтық программалаудың негізгі есебінің бос емес жиынтығы дөңес көпжақ (көп қырлы дене) түзеді. Осы көпжақтың әрбір ұшы тірек жоспарын анықтайды. Шешім көпжағының бір ұшындағы (яғни тірек жоспарларының бірі үшін) мақсатты функцияның (функция жоғары жағынан жоспарлар жиынтығына шектелген болған жағдайда) мәні максимальді болып табылады. Егер функция максимальді мәнді бір ұштағыдан да көп қабылдаса, онда ол осы мәнді аталмыш ұштардың сызықтық комбинациясының дөңесі болып табылатын кез келген нүктеде қабылдайды.
Мақсатты функция максимальді мәні қабылдайтын шешім көпжағының ұшын салыстырмалы түрде табу оңай, егер стандартты формада жазылған есеп құрамы екі айнымалыдан көп болмаса немесе негізгі формада жазылған есеп құрамы екі еркін айнымалыдан көп болмаса, яғни
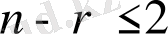 , мұндағы
, мұндағы
 -
айнымалылар саны,
-
айнымалылар саны,
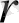 -
есептерді шектеу жүйесіндегі коэффициенттерден құралған матрицалар рангі.
-
есептерді шектеу жүйесіндегі коэффициенттерден құралған матрицалар рангі.
 (19)
(19)
 . (20)
. (20)
болса
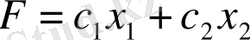 (21)
(21)
функциясының максимальді мәнінің анықтамасынан тұратын есеп шешімін табамыз.
Есепті шектеу жүйесі теңсіздігінің әрқайсысы геометриялық түрде
 шектес түзулерге сәйкесті жарты жазықтықты анықтайды. Егер (19), (20) теңсіздік жүйесі бірлескен болса оның шешілу алаңында көрсетілген барлық жарты жазықтықтарға жататын нүктелер жиыны бар. Аталмыш жарты жазықтықтардың қиылысу нүктелерінің жиыны дөңес болғандықтан, есептің шектеулі шешімінің аясы (19) - (21) шешімнің көпбұрышы (бұрын енгізілген «шешімнің көпжағы» деген термині әдетте n>3 болса қолданылады) деп аталатын дөңес жиын болып табылады. Осы көпбұрыштың қабырғалары теңдеуі теңсіздік белгілерінің дәл теңдік белгілеріне алмасуды шектеудің бастапқы жүйесінен алынатын түзулерде жатады.
шектес түзулерге сәйкесті жарты жазықтықты анықтайды. Егер (19), (20) теңсіздік жүйесі бірлескен болса оның шешілу алаңында көрсетілген барлық жарты жазықтықтарға жататын нүктелер жиыны бар. Аталмыш жарты жазықтықтардың қиылысу нүктелерінің жиыны дөңес болғандықтан, есептің шектеулі шешімінің аясы (19) - (21) шешімнің көпбұрышы (бұрын енгізілген «шешімнің көпжағы» деген термині әдетте n>3 болса қолданылады) деп аталатын дөңес жиын болып табылады. Осы көпбұрыштың қабырғалары теңдеуі теңсіздік белгілерінің дәл теңдік белгілеріне алмасуды шектеудің бастапқы жүйесінен алынатын түзулерде жатады.
Осылайша, сызықтық программалаудың бастапқы есебі
 мақсатты функциясы максимальді мәнді қабылдайтын көпбұрыш шешімінің нүктесін табудан тұрады. Бұл нүкте көпбұрыш шешімі болмағанда және ондағы мақсатты функция жоғарыдан шектеулі болғанда бар болады. Көпбұрыш шешімі ұштарының біріндегі көрсетілген шарттарда мақсатты функция максимальді мәнге ие болады. Аталған ұшты анықтау үшін шешім көпбұрышы арқылы өтетін
мақсатты функциясы максимальді мәнді қабылдайтын көпбұрыш шешімінің нүктесін табудан тұрады. Бұл нүкте көпбұрыш шешімі болмағанда және ондағы мақсатты функция жоғарыдан шектеулі болғанда бар болады. Көпбұрыш шешімі ұштарының біріндегі көрсетілген шарттарда мақсатты функция максимальді мәнге ие болады. Аталған ұшты анықтау үшін шешім көпбұрышы арқылы өтетін
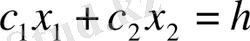 (мұндағы
(мұндағы
 - аз ғана тұрақты шама) деңгейінің сызығын құрамыз және оны
- аз ғана тұрақты шама) деңгейінің сызығын құрамыз және оны
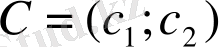 векторының бағытында ол вектордың шешім көпбұрышымен ортақ соңғы нүктесінен өткенге дейін жылжытамыз. Көрсетілген нүктенің координаттары берілген есептің тиімді жоспарын анықтайды.
векторының бағытында ол вектордың шешім көпбұрышымен ортақ соңғы нүктесінен өткенге дейін жылжытамыз. Көрсетілген нүктенің координаттары берілген есептің тиімді жоспарын анықтайды.
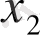
4 сурет
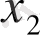
5 сурет
(8) - (21) есептерінің геометриялық түсіндірілуін қарастыруды аяқтай келе, оның шешімін табу барысында 4-7-суреттерінде суреттелген жағдайлар кездесуі мүміндігін атап өтеміз. 4-суреті мақсатты функция жалғыз
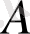 нүктесіндегі максимальді мәнді қабылдағандағы жағдайды сипаттайды. 5-суретінен мақсатты функция максимальді мәнді
нүктесіндегі максимальді мәнді қабылдағандағы жағдайды сипаттайды. 5-суретінен мақсатты функция максимальді мәнді
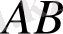 кесігінің кез келген нүктесінен қабылдайтыны көрініп тұр. 6-суретінде мақсатты функция жоғарыдан шектеулі шешімдер жиынына шектелмеген жағдайы, ал 7-суретте - есептің шектеу жүйесі бірлеспеген жағдайы көрсетілген.
кесігінің кез келген нүктесінен қабылдайтыны көрініп тұр. 6-суретінде мақсатты функция жоғарыдан шектеулі шешімдер жиынына шектелмеген жағдайы, ал 7-суретте - есептің шектеу жүйесі бірлеспеген жағдайы көрсетілген.
Көрсетілген шектеу жүйесі кезіндегі сызықтық функцияның максимальді мәнін табу сол шектеулердегі оның максимальді мәнін табудан айырмашылығы -
 деңгейінің сызығы
деңгейінің сызығы
 векторы бағытында емес қарама-қарсы бағытында жылжитынында ғана.
векторы бағытында емес қарама-қарсы бағытында жылжитынында ғана.
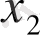
6 сурет
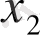
6 сурет
Осылайша, мақсатты функцияның максимальді мәнін табуда ұшырасқан жоғарыда айтылған жағдайлар оның минимальді (ең аз) мәнін анықтауда да орын алады.
Сөйтіп, геометриялық түсіндіру негізінде сызықтық программалау есептерінің (19) -(21) шешімін табу келесі кезеңдерден тұрады:
- Шектеулердегі (19) және (20) теңсіздік белгілерінің дәл теңдік белгілеріне алмасуы нәтижесінде алынатын түзу теңдеулер құрады.
- Есеп шектеуінің әрқайсысымен анықталатын жарты жазықтықтарды табады.
- Шешім көп бұрышын табады.
- векторын құрады.
- Шешім көпбұрышы арқылы өтетінтүзуін құрады.
- түзуінвекторының бағытында жылжытады, нәтижесінде мақсатты функция максимальді мән қабылдайтын нүктені табады немесе жоспарлар жиынына функцияның жоғарынан шексіздік орнатады.
- Функция максимумы нүктесінің координаттарын анықтайды және осы нүктедегі мақсатты функцияның мәнін есептеп шығарады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz