Модельдеу теориясының негізгі ұғымдары мен әдістері: математикалық, аналитикалық, имитациялық және сандық іске асыру


Дәріс № 1
Моделдеу теориясының негізгі ұғымдары.
Дәріс мақсаты:
1. Моделдеу теориясының негізгі ұғымдары. Моделдеу анықтамасы.
2. Моделдеу принципі.
3. Математикалық моделдеу кезеңдері.
4. Аналитикалық және еліктеулік моделдеу.
Моделдеу - ол зерттелетін объектіні оның шартты бейнесімен немесе басқа кескінмен ауыстыру және түп нұсқаның қасиеттерін бейненің қасиеттері зерттеу жолымен оқып білу.
Сірә, моделдеуден келетін нақты пайда тек қана екі шартты сақтаған кезде ғана болуы мүмкін:
• зерттеу операциясының көзқарасы бойынша модель түпнұсқа қасиетіне барабар кескінмен қамтамасыз етеді;
• модель жоғарыда айтылған, нақты объектілерді өлшеу кезінде болатын қиындықтарды жоюға мүмкіндік береді.
Орындалу әдістеріне байланысты, бүкіл моделдерді екі үлкен классқа бөоуге болады: физикалық және математикалық.
Физикалық моделдер түп нұсқаның керекті физикалық қасиеттерін нақты түрде іске асыруды болжайды. Мысалы, жаңа ұшақты жобалаған кезде шын ұшақтың аэродинамикалық қасиеттеріндей қасиеті бар, оның макеті жасалады; құрылысты жобалаған кезде архитекторлар оның элементтерінің кеңістікте қалай орналасуы керектігін көрсететін макет дайындайды. Осыған байланысты физикалық моделдеуді сонымен қатар макеттендіру деп те атайды.
Математикалық модель жүйені (немесе операцияларды) қандайда бір абстракталық тілдегі өрнектер түрінде жазуды көрсетеді, мысалы математикалық қатынастардың немесе алгоритмдер сұлбасының жиынтықтары түрінде. Сондықтан, оларда физикалық шамалар ескерілетін кез-келген математикалық өрнектерді сол немесе басқа үрдістердің немесе құбылыстардың математикалық моделі ретінде қарастыруға болады. Мысалы, бәрімізге бастапқы мектептен белгілі
 теңдеуі бірқалыпты түзу сызықты қозғалыстың моделін көрсетеді. Атап айтқанда математикалық моделдерді біз мұнан былай балама стратегияларды тиімді бағалайтын негізгі құрал ретінде қарастыратын боламыз.
теңдеуі бірқалыпты түзу сызықты қозғалыстың моделін көрсетеді. Атап айтқанда математикалық моделдерді біз мұнан былай балама стратегияларды тиімді бағалайтын негізгі құрал ретінде қарастыратын боламыз.
Компьютерлік моделдеу - бұл есептеу техникаларын пайдаланатын математикалық моделдеу.
Аналитикалық моделдеу шектеу жүйелерімен толықтырылған, шықпалық айнымалыларды кірмелікпен байланыстыратын нақты объектінің математикалық моделін алгебралық, дифференциалдық, интегралдық және де басқа теңдеулер түрінде қолдануды болжайды. Бұл кезде теңдеу дәл шешіледі деп болжанылады.
Өліктеулік моделдеу кезінде пайдаланылатын математикалық модель зерттелетін жүйенің уақыт бойынша, жүйенің және сыртқы ортаның параметрлерінің үйлесімді әртүрлі мәндері кезіндегі жұмыс алгоритмін жасайды.
Қарапайым аналитикалық моделге бірқалыпты түзу сызықты қозғалыстың теңдеуі мысал болуы мүмкін. Мұндай үрдісті имитациялық моделдің көмегімен зерттеген кезде уақыттың өтуімен жүрілген жолдың өзгеруін бақылауды іске асыру керек. Кейбір жағдайларда аналитикалық моделдеуді пайдаланған тиімді болса, басқа бір жағдайларда имитациялық (немесе екеуін сәкестендіріп) моделдеуді қолдану тиімді болады. Таңдау сәтті болу үшін, екі сұраққа жауап беру қажет.
Нақты модель жасағанда моделдеу мақсаты, ресурстар мен уақытқа және операцияның пайдалы тиімділігіне жұмсалатын қаржыны ескеретін, пайдаланылатын тиімділіктің өлшемін анықтап алу.
Сонымен қатар, моделдеу мақсаты зерттеу операциясының мақсатымен және зерттеу нәтижесін пайдалану әдісін жоспарлауды анықтау.
1. 1 Моделдеу принциптері
Ақпараттық жеткіліктілік принципі . Зерттелетін жүйе жөнінде толық ақпарат болмаған кезде оның моделін құру мүмкін емес. Жүйе жөнінде ақпарат толық болған кезде оны моделдеудің мағынасы жоқ. Жүйе жөніндегі априорлық мәліметтің кейбір аумалы деңгейі болады (ақпараттың жеткіліктілік деңгейі), осыған жеткен кезде оған барабар модель құрылуы мүмкін.
Іске асырылу принципі.
Жасалатын модель зерттеуге қойылІске асырылу принципі. Жасалатын модель зерттеуге қойылған мақсатқа жету мүмкіндігінің нөлден өзгеше және шектелген уақытта болуын қамтамасыз етуі қажет. әдетте моделдеу мақсатына жету мүмкіндігі
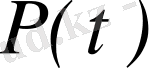 болатын қандайда бір
болатын қандайда бір
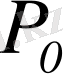 мәні, сондай-ақ осы мақсатқа жету уақытының қабылданған шекарасы беріледі. Егер
мәні, сондай-ақ осы мақсатқа жету уақытының қабылданған шекарасы беріледі. Егер
 шартының орындалуы мүмкін болса, моделді іске асыруға болады деп есептейді.
шартының орындалуы мүмкін болса, моделді іске асыруға болады деп есептейді.
Моделдердің көптік принципі. Бұл кілттік принцип болады. Жаслатын модель бірінші кезекте нақты жүйенің (немесе құбылыстың) таңдалған тиімділіктің көрсеткішіне әсер ететін қасиеттерін көрсету керек. Осыған сәйкес кез келген нақты моделді пайдаланған кезде шындықтың кейбір жақтары ғана білінеді. Оны толығырақ зерттеу үшін, қарастырылатын үрдісті жан-жақты және әртүрлі деңгейде көрсетуге мүмкіндік беретін бірнеше моделдер керек болады.
Агрегаттау принципі. Көптеген жағдайда күрделі жүйені агрегаттардан құралатын етіп көрсетуге болады, оларды бірдей математикалық түрде бейнелеуге біраз стандартты математикалық сұлбалар жарамды болады екен. Агрегаттау принципі, бұдан басқа, моделді зерттеу мақсатына байланысты қайта жасауға мүмкіндік береді.
Параметрлеу принципі. Көптеген жағдайда моделдендіретін жүйенің құрамына белгілі параметрлермен, соның ішінде векторлармен сипатталатын кейбір оқшауландырылған қосалқы жүйелер болады. Мұндай қосалқы жүйелерді моделде, олардың жұмыстың үрдістерін баяндап жатпай, оларға сәйкес сандық шамалармен ауыстыруға болады. Бұл шамалардың жағдайға байланысты мәндерінің тәуелділігі қажет болған жағдайда оларды кесте түрінде, график немесе аналитикалық өрнектер түрінде беруге болады. Параметрлеу принципі моделдеу көлемін және мерзімін ықшамдауға мүмкіндік береді. Дегенмен параметрлеу моделдің түп нұсқасымен бірдей болуын төмендететінін ескеру керек.
1. 2 Математикалық моделдеу кезеңдері
Компьютерлік моделдеу технологиясы келесідей әрекеттерді орындау керек деп болжайды.
1. Моделдеу мақсатын анықтау.
2. Мазмұнды модел дайындау.
3. Моделдерді түрлендіру.
4. Моделді бағдарламалық іске асыру.
5. Моделдік эксперименттерді жоспарлау.
6. Эксперимент жоспарын жүзеге асыру.
7. Моделдеу нәтижелерін талдау және түсіндіру.
Бірінші екі кезеңнің мазмұны іс жүзінде, моделдеу негізінде алынған, математикалық әдіске тәуелсіз болады (керісінше - олардың нәтижесі әдісті таңдайды) .
Ал соңғы бес кезеңді іске асыру модель құратын негізгі екі әдістің әрқайсысы үшін елеулі айырмашылықта болады.
Мысалы, шешім қабылдауды қажет ететін, проблемалық жағдай, келесі түрде тұжырымдалады:өнімділігі бойынша және сенімділігі бойынша қойылатын талаптарды сақтаған кезде оның құны ең аз болатын, есептеу желілерін құру нұсқаларын табу. Бұл жағдайда моделдеудің мақсаты тиімділік көрсеткішінің (ТЭ) ең аз мәнін қамтамасыз ететін желінің параметрлерін іздестіру болады, яғни құнын.
Мақсат басқаша тұжырымдалуы мүмкін: есептеу желілерінің бірнеше құрылымдық нұсқаларының ішінен ең сенімдісін таңдап алу. Мұнда тиімділік көрсеткіші ретінде сенімділік көрсеткішінің бірі алынады (тоқтап қалғанға дейінгі орташа жұмыс істеуі, тоқтамай жұмыс істеу мүмкіндігі және т. б. ), ал моделдеу мақсаты осы көрсеткіш бойынша желінің нұсақаларын салыстырып бағалауға болады.
Келтірілген мысалдар, тиімділік көрсеткішін таңдау келешек моделдің «архитектурасын» анықтамайтынын, себебі бұл кезеңде ол туралы негізгі пікір қалыптаспайтынын, немесе, былайша айтқанда, зерттелетін жүйенің мазмұнды моделі анықталмайтынын еске салуға мүмкіндік береді.
Мазмұнды модель - бұл моделдендірілетін жүйенің құрылымын, оның элементтерінің және моделдеу мақсатына жету үшін маңызды қасиеттерін анықтайтын абстрактты модель.
Аналитикалық моделдеу нақты объектінің алгебралық, дифференциалдық, интегралдық және шықпалық айнымалыны кірмелікпен байланыстыратын, шектеу жүйелерімен толықтырылған басқа да теңдеулер түріндегі математикалық моделін пайдалануды болжайды. Бұл кезде теңдеуді дәл шешетін есептеу жолдары болуын болжайды.
Дәріс № 2
Аналитикалық моделдеу. Жалпыланған электромеханикалық түрлендіргіштерді моделдеу (ЖЭМТ)
2. 1 ЖЭМТ математикалық моделін құру
Моделдеу мақсаты: ЖЭМТ динамикалық және статикалық қасиеттерін есептегіш машиналармен зерттеу үшін математикалық модель дайындау.
2. 1. 1 ЖЭМТ концептуалдық моделі
ЖЭМТ - статорда немесе роторда екі-екіден орамалары бар, екіполюсті және екі фазалы симметриялы идеалды электрлік машина (1-сурет) .
Идеалдау (ұйғару) :
1. Машина толықтай симметриялы;
2. Магниттік тізбектің қанығуы ескерілмейді;
3. Статор мен ротордың тістері ескерілмейді;
4. Полюстің айқындалмауы магниттік индукцияның остер бойынша бірдей болмай таралуымен ескеріледі.
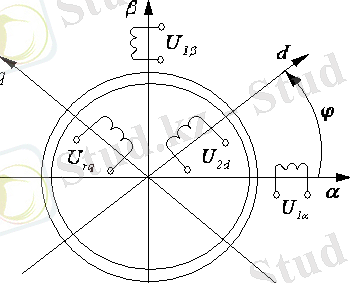
1-сурет. ЖЭМТ кеңістіктік моделі
Суретте: α, β - машина статорымен қатаң байланысқан, ортогоналдық координат жүйесі. d, q - машинаның роторымен қатаң байланысқан, ортогоналдық координат жүйесі.
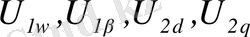 - статордың және ротордың остері бойынша кернеулері.
- статордың және ротордың остері бойынша кернеулері.
2. 1. 2 Моделдің сыртқы пішіні
Объектінің математикалық моделі аналитикалық болады, яғни дифферциалдық және алгебралық теңдеулер жүйелері түрінде құрылады.
ЖЭМТ электрлік тепе-теңдігінің дифференциалдық теңдеулер жүйесі төрт орама үшін жазылған Кирхгофтың төрт теңдеуінен тұрады
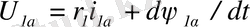 (2. 1)
(2. 1)

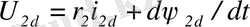
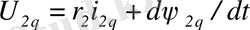 ,
,
мұнда
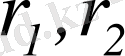 - статор мен ротордың активті кедергілері;
- статор мен ротордың активті кедергілері;
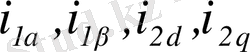 - статор және ротор орамаларының токтары.
- статор және ротор орамаларының токтары.
Толық магниттік ағындар остер бойынша келесідей өрнекпен анықталады:
 (2. 2)
(2. 2)


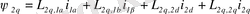
Индуктивтіліктердегі
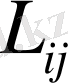 индекстер, қандай орамада және қандай ораманың (
индекстер, қандай орамада және қандай ораманың (
 ) тоғымен толық магнит ағыны пайда болғанын белгілейді. Теңдеулерді келесі түрде қайта жазуға болады:
) тоғымен толық магнит ағыны пайда болғанын белгілейді. Теңдеулерді келесі түрде қайта жазуға болады:
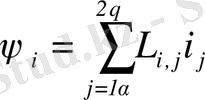 (2. 3)
(2. 3)
 (2. 4)
(2. 4)
(2. 1) теңдеулер жүйесін бірге шешу мүмкін емес, себебі теңдеулер әртүрлі координат жүйелерінде жазылған. (2. 1), (2. 2) теңдеулерді статордың координат жүйесінде көшіріп жазуға болады:
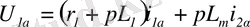 (2. 5)
(2. 5)


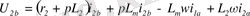 ,
,
мұнда
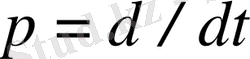 - дифферециалдау операторы.
- дифферециалдау операторы.
 - статордың, ротордың толық индуктивтілігі және өзара индуктивтілік.
- статордың, ротордың толық индуктивтілігі және өзара индуктивтілік.
Матрица түрінде жазылуы:
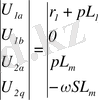
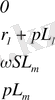

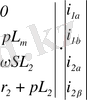 (2. 6)
(2. 6)
ЭМТ статоры мен роторының өрістері өзара әрекеттесіп электромагниттік момент туғызады.
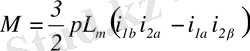 (2. 7)
(2. 7)
(2. 6), (2. 7) теңдеулер қозғалыс теңдеуімен бірге
 (2. 8)
(2. 8)
энергияның электромеханикалық түрлену үрдісін бейнелейді.
Дәріс № 3
Моделді бағдарламалық іске асыру
Дәріс мақсаты: Дифференциалды теңдеуді аналитикалық жолмен шешу
Математикалық моделді пішіндеген кезде берілген динамикалық үрдісті бейнелейтін дифференциалдық теңдеуді (немесе теңдеулер жүйесін) шешетін әдіс таңдау керек. Символдық (аналитикалық) әдістер ең дәл және артықшылығы бар, бірақ әрқашан іске асырылмайды. Символдық әдіспен есептеу жүргізуге символдық математика пакеттерін «Maple» немесе «Mathematica» пайдалану үлкен көмек көрсетуі мүмкін.
Қазіргі есептік әдістерді пайдалану жуықтап есептейтін сандық әдістердің дәлдігін, олардың тездігін айтарлықтай өсірді. Көптеген математикалық компьютерлік қосымшалар сандық есептеу әдістерін қолдануды ықшамдайды және оларды әмбебап жасайды. Модельді аналитикалық әдіспен қарапайым түрде бейнелеп және шешетін жағдай болса, онда соңғысына жол берген дұрыс. Қазіргі кезде, инженерлік есептеулер үшін ең көп таралған математикалық қолтаңбалы бағдарламамен «Mathcad» және «Matlab».
3. 1 Дифференциалды теңдеуді аналитикалық шешуге мысал
Дифференциалдық теңдеулерді аналитикалық шешуге мысалды қарапайым электрлік схемаға (1-сурет) қарастырамыз.
а) Классикалық әдіс.

1-сурет
Бірінші реттік дифференциал теңдеумен бейнеленетін, қарапайым звеноны қарастырамыз
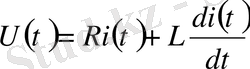
Кілт тұйықталған кезде токтың қалыптасқан мәніне дифференциал теңдеудің жеке шешімі сәйкес келеді деп қабылдаймыз
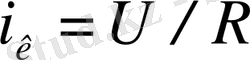
Бұл шешімді қалыптаспаған үрдісті бейнелейтін, бір текті дифференциал теңдеудің шешімімен қосады:

Шешуі
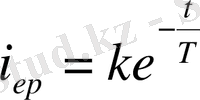 ,
,
мұнда
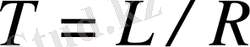 - уақыт тұрақтысы.
- уақыт тұрақтысы.
Уақыт
 болған кезде, осыған дейін нөлге тең болған ток, лезде өзгере алмайды деген шартты ескеріп, бұл екі шешімді қосамыз:
болған кезде, осыған дейін нөлге тең болған ток, лезде өзгере алмайды деген шартты ескеріп, бұл екі шешімді қосамыз:
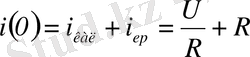
Сондықтан,

және толық шешуі
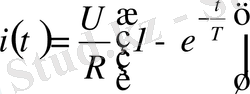
б) Операторлық әдіс.
ДТ операторлық әдіспен шешу теңдеудің функцияларын - түп нұсқаларды Лапластың түрлендірулеріне сәйкес олардың бейнелерімен ауыстыруды қарастырады, алынған алгебралық теңдеуді шешеді (мұнда дифференциалдау және интегралдау көбейтумен және бөлумен ауыстырылады) және алынған нәтиже кері қарай түрлендіріледі.
Екі жағдайда да, тіпті қарапайым теңдеуді шешу үшін де көп уақыт кетеді. ЖЭМТ үшін жазылған Кирхгофтың теңдеулерін аналити калық әдіспен шешу статор мен ротор фазаларындағы өзара индуктивтіліктерді есептеуге байланысты қиындайды. (2. 6) - (2. 8) теңдеулерді, момент теңдеуі сызықсыз болатындықтан, біріктіріп аналитикалық түрде шешу мүмкін емес. ДТ бұл жүйелерін сандық жолмен шешуге альтернатив жоқ.
Дәріс № 4
Моделді бағдарламалық іке асыру
Дәріс мақсаты: Дифференциалдық теңдеулерді және дифференциалдық теңдеулер жүйесін сандық әдіспен жуықтап шешуді үйрену
Іс жүзінде динамикалық жүйені және олардың математикалық моделдерін талдауға қатысты барлық есептер, ДТ жүйесін сандық әдістерді қолданып шешуге негізделген.
Жалғыз дифференциал теңдеуді шешетін қарапайым сандық әдіс Эйлер әдісі болады
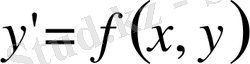
Ол келесі рекурренттік формуламен іске асырылады:

Мұнда
 - шешу қадамы. Бұл әдістің қателігі айтарлықтай, сондықтан ол іс жүзінде қолданылмайды десе де болады.
- шешу қадамы. Бұл әдістің қателігі айтарлықтай, сондықтан ол іс жүзінде қолданылмайды десе де болады.
Суретте модификацияланған Эйлер әдісін «Mathcad»та пайдаланып іске асыру берілген, оның қателігі
 жақын (яғни
жақын (яғни
 болған кезде 1% болады), бұл бірінші реттегі дифференциал теңдеуді шешуге сирек қолданылатынын білдіреді.
болған кезде 1% болады), бұл бірінші реттегі дифференциал теңдеуді шешуге сирек қолданылатынын білдіреді.
Бұл әдісті қолданған кезде есептеу дәлдігін жақсартуға, интегралдауды тікбұрыштар әдісінің орнына трапеция әдісін қолдану арқылы қол жеткізуге болады.
4. 1 Бірінші реттік дифференциалдық теңдеуді Рунге-Кутта әдісімен шешу
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz