Электрэнергетикадағы математикалық есептер және компьютерлік моделдеу - есептік-графикалық жұмыстарына әдістемелік нұсқаулар
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
КОММЕРЦИЯЛЫҚ ЕМЕС АКЦИОНЕРЛІК ҚОҒАМЫ
«Өндіріс кәсіпорындарын электрмен жабдықтау» кафедрасы
Электрэнергетикадағы математикалық есептер және компьютерлік моделдеу
5В071800 - Электр энергетика мамандығының студенттерінің №1 есептік-графикалық жұмыстарына әдістемелік нұсқаулар
Алматы 2010
ҚҰРАСТЫРУШЫ: К. А. Бакенов, M. А. Тергеусизова. Электрэнергетикадағы математикалық есептер және компьютерлік моделдеу. 5В071800 - Электр энергетика мамандығының студенттерінің №1 есептік-графикалық жұмыстарына әдістемелік нұсқаулар. - Алматы: АЭжБУ, 2010. -20 б.
Мазмұны
Кіріспе
Оқу жоспарына сәйкес, 5В071800 - Электрэнергетика мамандығы бойынша оқытылатын студенттер «Электроэнергетикадағы компютерлік моделдеу және математикалық есептер» курсын оқиды, онда студенттердің өткен пәндер бөлімінен өзіндік қайталауға мүмкіндік беретін әрқайсысы үш тапсырмадан тұратын екі есептік-графикалық жұмыс қарастырылған.
Курс бойынша емтиханға тек есептік-графикалық жұмысты жақсы орындап қорғаған студенттер жіберіледі.
1 Тапсырма №1. Графикалық әдіспен сызықты теңдеулер жүйесін шешу. Тапсырмаға сәйкес функция экстремумының нүктесін анықтау және рұқсатты шешім ауданын тұрғызу
Есепке алғашқы мәліметтер 1. 1, кесте бойынша нұсқаларды таңдау ережесіне сәйкес жүргізіледі.
Кесте 1. 1 - Алғашқы мәліметтер
А,
Д
Б,
Е
В,
Г,
Я
Ж,
З,
И,
Л
К,
Ю
М,
О
Н,
П
Р,
Т,
У,
Ф
С,
Ч,
Ц
Х,
Ш,
Щ,
Э
Мақсаттық
функция
элементтері
1. 1 Әдістемелік нұсқаулар
Сызықты теңдеулер жүйесін графикалық әдіспен шешу. х 2 ×х 1 координат жүйесінде теңсіздікті а 1 х 1 +а 2 х 2 =а 0 шекті түзу жарты жазықтықты анықтайды.
Егер теңсіздіктер жүйесі берілген болса, онда рұқсатты шешімдер ауданын (РША) тұрғызу үшін шекаралық түзулер тұрғызады, содан теңсіздіктер мәліметтері орындалатын жартылай жазықтықтар орындалады.
РША (төбе) координаттарын алу үшін, осы төбелерде түйісетін түзулер теңдеулер жүйесін шешу керек.
n>2 санынында теңсізді
а
1
х
1
+ а
2
х
2
+ . . . + а
n
х
n
а
0
теңдеуге эквивалентті
а 1 х 1 + . . . + а n х n +х n+1 = а 0 ; х n +1 ≥0 және
а 1 х 1 + . . . + а n х n ≥0.
сәйкесінше а 1 х 1 + . . . + а n х n -х n+1 =0.
х n+1 айнымалысын қосымша ( баланстық) деп атайды.
Егер теңсіздік жүйесі берілсе
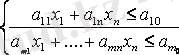
онда оны эквиваленнті сызықты теңдеулер жүйесінің (n+m) айнымалылармен алмастыруға болады.
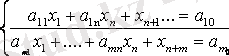
мұнда
Вектор-потенциал
, тура басизті айнымалыларға перпендикуляр, ол f функциясының жылдам өсу бағытын көрсетеді, ал вектор
f функциясының жылдам төмендеуіне бағытталған.
Берілген есеп Mathcad программасының көмегімен шешіледі. Бұл үшін функция теңдеуіне сәйкес 1. 1, кестесінен берілген мәліметтерді енгізу қажет, ал 1. 2, кестесінен шектеу теңдеуіне сәйкес мәліметтерді алу қажет. Алынған шешімдерді теріс емес принцип бойынша орындауға талаптар қою.
1. 2 кесте - Алғашқы мәліметтер
Элеменнтер
А i. B i. C ii
0
1
2
3
4
5
6
7
8
9
Тұтыну қуаты және қуат бірлігінің берілу құны
Қорек көздері нің қуаты, А i. j
а 13
Тұтынушылар қуаты
B j
b 1
b 3
b 4
Шектеу белгілері
(
)
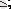
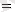1
2
Графикте рұқсатты шешімдер және векторпотенциал ауданын тұрғызу, оның бағыты бойынша функцияның экстремум нүктелерін және оның координаттарын анықтау. Экстремум нүктесінде айнымалыларды және функция мәнін анықтау.
1. 2 Мысал
f( х 4, х 5 ) = 4х 4 +х 5
Given
5х 1 -2х 2 +2х 3 +х 4 -х 5 = 13
2х 1 -2х 2 +х 3 -х 4 +х 5 = 5
х 1 +2х 2 +4х 4 -2х 5 = 5
Find (х
1,
х
2,
х
3,
х
4,
х
5
)
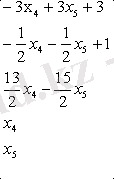
Ары қарай х 4 және х 5 тәуелділігінен шектеулі теңдеу өрнегін тұрғызу қажет.
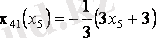
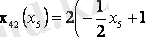
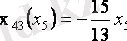
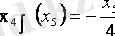
График бойынша потенциал-вектор бағытын анықтаймыз, қазіргі жағдайда оның координаттары (0, 0) және (4, 1) ; содан кейін осы векторға перепендикуляр тұрғызамыз, ол арқылы біз функцияның жылдам өсу бағытын анықтаймыз.
Перпендикулярдың ОДР мен қилысқан бірінші нүктесі min функция болып табылады, ал соңғысы - max. Біздің жағдайда: min ƒ (0, 0), ал max ƒ (1, 1) .
Алынған мәндермен барлық айнымалылар және экстремум нүктесіндегі фунция мәні анықталады.
График саламыз.
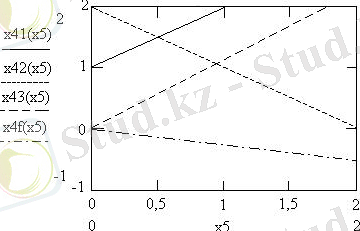
х 1 (х 4, х 5 ) = 3: х 2 (х 4, х 5 ) = 0: х 3 (х 4, х 5 ) = -1;
махƒ(х 4, х 5 ) → 5; minƒ(х 4, х 5 ) = 0.
2 Тапсырма №2. Синхронды қозғалтқыштардың оңтайлы реактивті қуатын Лагранждың анықталмаған көбейткіштер әдісімен анықтау
Өндірістік өнеркәсіптің ТҚ 6-10 шиналарына N синхронды электрқозғалтқыштар қосылған, Лагранждың анықталмаған көбейткіштер әдісі арқылы кәбілдер кедергісін ескермей әрбір синхронды қозғалтқышының тиімді реактивті қуатын анықтау керек. 6-10 кВ жағындағы компенсацияға жататын реактивті жүктеме есеп нұсқасымен анықталады.
Әрбір нұсқаның есепке берілген мәліметтері 2. 1, 2. 2 және 2. 3 кестесінен анықталады. Қозғалтқыштардың техникалық сипаттамалары 2. 4 кестесінде берілген.
2. 1 Кесте - Алғашқы мәліметтер
2. 2 Кесте - Алғашқы мәліметтер
Компенсацияға
жататын қуат
2. 3 Кесте - Алғашқы мәліметтер
А,
Д
Б,
Е
В,
Г,
Я
Ж,
З,
И,
Л
К,
Ю
М,
О
Н,
П
Р,
Т,
У,
Ф
С,
Ч,
Ц
Х,
Ш,
Щ,
Э
2. 1 Әдістемелік нұсқау
Есепті Лагранж көбейткіштері тәсілімен шығарғанда f мақсаттық функциясы және φ i шектуі беріледі. Есеп шектеулі φ i (х 1 . . . х n ) = b i функция экстремум нүктесінде х 1 , х 2 . . . , х n , табу болып табылады.
Әдістің негізгі мақсаты фунция кейбір бір шешімге түрлендіру, ол үшін есеп шешімі шығарылып және шартты экстремум анықталады. Функцияны, айнымалылар саны екіге тең кезінде қарастырамыз.
f(x 1 , x 2 ), (2. 1)
φ i (х 1 . . . х n ) = 0. (2. 2)
Берілген шартқа Лагранж функциясының түрі келесідей болады
L (x 1 , x 2, λ) = f(x 1 , x 2 ) + λ[b-φ(x 1 , x 2 ) ] (2. 3)
мұнда λ - Лагранж көбейткіші, шартсыз экстремум, ол шартты экстремуммен f (x 1 , x 2 ) және λ мән саны шектеу санына тәуелді.
2. 4 Кесте - Алғашқы мәліметтер
Кернеу
U н , кВ
Активті
Р н , кВт
Реактивті
Q н , квар
1250
1600
4000
645
817
2010
6, 77
7, 58
10, 6
6, 98
7, 56
11, 8
4000
3200
2010
1615
14, 2
12, 2
13, 0
12, 3
2. 4 кестенің жалғасы
1250
1600
3200
4000
637
820
1620
2010
8, 6
9, 43
10, 3
11, 3
6, 05
8, 24
13, 6
13, 6
1250
3200
4000
642
1620
2039
9, 08
9, 72
16, 4
8, 53
11, 2
15, 4
1600
3200
825
1625
10, 3
14, 7
10, 4
14, 7
1250
3200
645
1620
9, 71
14, 0
8, 07
15, 1
1250
1600
3200
650
825
1635
9, 96
11, 1
18, 2
8, 83
9, 51
14, 4
1000
6300
511
3150
5, 09
14, 6
3, 99
13, 1
6300
2500
800
3150
1265
407
18, 1
11, 2
4, 9
14, 8
10, 2
4, 57
6300
2500
1000
3150
1265
511
17, 1
10, 9
7, 66
14, 4
8, 46
5, 38
6300
2500
1000
800
400
3160
1265
511
412
209
21, 0
11, 5
6, 61
6, 48
3, 88
16, 3
9, 36
5, 88
5, 54
2, 97
1000
2500
520
1270
10, 0
15, 9
7, 19
11, 7
2500
800
400
1270
416
211
15, 3
7, 76
5, 13
10, 7
6, 00
5, 08
800
400
423
216
10, 5
7, 64
8, 3
4, 25
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz